Función convexa

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Función convexa en un intervalo.

Función real con línea de secant entre puntos por encima del propio gráfico

Una función (en negro) es convexa si y sólo si la región por encima de su gráfico (en verde) es un conjunto convexo.

Un gráfico de la función bivariada convexa x² + xy + Sí.².

Convex vs. No convexo

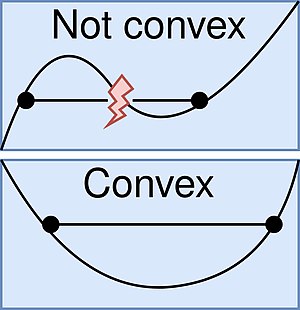
En matemáticas, una función de valor real se llama convex si el segmento de línea entre dos puntos distintos en el gráfico de la función se encuentra por encima del gráfico entre los dos puntos. Equivalentemente, una función es convexa si su epígrafe (el conjunto de puntos sobre o sobre el gráfico de la función) es un conjunto convexo. Una función dos veces diferenciable de una sola variable es convex si y sólo si su segundo derivado es no negativo en todo su dominio. Ejemplos conocidos de funciones convexas de una sola variable incluyen una función lineal ${displaystyle f(x)=cx}$ (donde) $c$ es un número real), una función cuadrática ${displaystyle cx^{2}}$ () $c$ como un número real no negativo) y una función exponencial ${displaystyle ce^{x}}$ () $c$ como un número real no negativo). En términos simples, una función convexa se refiere a una función cuyo gráfico se forma como una taza $cup$ (o una línea recta como una función lineal), mientras que el gráfico de una función de cóncava se forma como una tapa $cap$ .

Las funciones convexas juegan un papel importante en muchas áreas de las matemáticas. Son especialmente importantes en el estudio de problemas de optimización donde se distinguen por una serie de propiedades convenientes. Por ejemplo, una función estrictamente convexa en un conjunto abierto no tiene más de un mínimo. Incluso en espacios de dimensión infinita, bajo hipótesis adicionales adecuadas, las funciones convexas continúan satisfaciendo tales propiedades y, como resultado, son las funciones mejor entendidas en el cálculo de variaciones. En la teoría de la probabilidad, una función convexa aplicada al valor esperado de una variable aleatoria siempre está limitada por arriba por el valor esperado de la función convexa de la variable aleatoria. Este resultado, conocido como desigualdad de Jensen, se puede utilizar para deducir desigualdades como la desigualdad de la media aritmético-geométrica y la desigualdad de Hölder.

Definición

Visualizar una función convex y la desigualdad de Jensen

Vamos $X$ ser un subconjunto convexo de un espacio vectorial real y dejar ${displaystyle f:Xto mathbb {R} }$ ser una función.

Entonces... $f$ se llama convex si y sólo si alguna de las siguientes condiciones equivalentes sostiene:

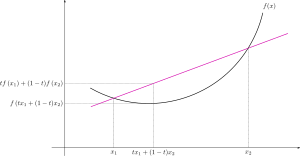
Para todos ${displaystyle 0leq tleq 1}$ y todos ${displaystyle x_{1},x_{2}in X}$ : ${displaystyle fleft(tx_{1}+(1-t)x_{2}right)leq tfleft(x_{1}right)+(1-t)fleft(x_{2}right)}$ El lado derecho representa la línea recta entre ${displaystyle left(x_{1},fleft(x_{1}right)right)}$ y ${displaystyle left(x_{2},fleft(x_{2}right)right)}$ en el gráfico de $f$ como función de ${displaystyle t;}$ creciente $t$ desde ${displaystyle 0}$ a $1$ o disminución $t$ desde $1$ a ${displaystyle 0}$ barre esta línea. Del mismo modo, el argumento de la función $f$ en el lado izquierdo representa la línea recta entre $x_{1}$ y $x_{2}$ dentro $X$ o el $x$ -eje del gráfico $f.$ Por lo tanto, esta condición requiere que la línea recta entre cualquier par de puntos en la curva de $f$ para estar arriba o conocer el gráfico.
Para todos $<math alttext="{displaystyle 0<t0.t.1{displaystyle 0 se hizo realidad] <img alt="{displaystyle 0<t$ y todos ${displaystyle x_{1},x_{2}in X}$ tales que ${displaystyle x_{1}neq x_{2}}$ : ${displaystyle fleft(tx_{1}+(1-t)x_{2}right)leq tfleft(x_{1}right)+(1-t)fleft(x_{2}right)}$ La diferencia de esta segunda condición con respecto a la primera condición anterior es que esta condición no incluye los puntos de intersección (por ejemplo, ${displaystyle left(x_{1},fleft(x_{1}right)right)}$ y ${displaystyle left(x_{2},fleft(x_{2}right)right)}$ ) entre la línea recta pasando por un par de puntos en la curva de $f$ (la línea recta está representada por el lado derecho de esta condición) y la curva ${displaystyle f;}$ la primera condición incluye los puntos de intersección ya que se ${displaystyle fleft(x_{1}right)leq fleft(x_{1}right)}$ o ${displaystyle fleft(x_{2}right)leq fleft(x_{2}right)}$ a $t=0$ o $1,$ o ${displaystyle x_{1}=x_{2}.}$ De hecho, los puntos de intersección no necesitan ser considerados en una condición de convex utilizando ${displaystyle fleft(tx_{1}+(1-t)x_{2}right)leq tfleft(x_{1}right)+(1-t)fleft(x_{2}right)}$ porque ${displaystyle fleft(x_{1}right)leq fleft(x_{1}right)}$ y ${displaystyle fleft(x_{2}right)leq fleft(x_{2}right)}$ son siempre verdaderas (no tan útiles para ser parte de una condición).

La segunda declaración caracterizando funciones convexas que se valoran en la línea real $mathbb {R}$ es también la declaración utilizada para definir funciones convex que se valoran en la línea de números reales extendidos ${displaystyle [-inftyinfty ]=mathbb {R} cup {pm infty },}$ donde tal función $f$ se permite tomar $pm infty$ como valor. La primera declaración no se utiliza porque permite $t$ para tomar ${displaystyle 0}$ o $1$ como valor, en cuyo caso, ${displaystyle fleft(x_{1}right)=pm infty }$ o ${displaystyle fleft(x_{2}right)=pm infty}$ respectivamente, entonces ${displaystyle tfleft(x_{1}right)+(1-t)fleft(x_{2}right)}$ sería indefinido (porque las multiplicaciones $0 cdot infty$ y ${displaystyle 0cdot (-infty)}$ son indefinidos). La suma $-infty +infty$ es también indefinido por lo que una función convexa de valor real extendido sólo se permite tomar exactamente uno de $-infty$ y $+infty$ como valor.

La segunda declaración también se puede modificar para obtener la definición de estricta convexidad, donde se obtiene este último sustituyendo ${displaystyle ,leq ,}$ con la estricta desigualdad $<math alttext="{displaystyle ,..{displaystyle , interpretado.} <img alt="{displaystyle ,$ Explícitamente, el mapa $f$ se llama estrictamente convex si y sólo si para todo real $<math alttext="{displaystyle 0<t0.t.1{displaystyle 0 se hizo realidad] <img alt="{displaystyle 0<t$ y todos ${displaystyle x_{1},x_{2}in X}$ tales que ${displaystyle x_{1}neq x_{2}}$ :

<math alttext="{displaystyle fleft(tx_{1}+(1-t)x_{2}right)f()tx1+()1− − t)x2).tf()x1)+()1− − t)f()x2){displaystyle fleft(tx_{1}+(1-t)x_{2}right) selecciontfleft(x_{1}right)+(1-t)fleft(x_{2}right)}<img alt="{displaystyle fleft(tx_{1}+(1-t)x_{2}right)

Una función estrictamente convexa $f$ es una función que la línea recta entre cualquier par de puntos en la curva $f$ está por encima de la curva $f$ excepto los puntos de intersección entre la línea recta y la curva.

La función $f$ se dice que concave (Resp. estrictamente cóncavoSi $-f$ () $f$ multiplicado por −1) es convex (resp. estrictamente convex).

Denominación alternativa

El término convex a menudo se conoce como Convex abajo o cóncava hacia arriba, y el término cóncavo se conoce a menudo como Concave abajo o convexo hacia arriba. Si el término "convex" se utiliza sin una palabra clave "up" o "down", entonces se refiere estrictamente a un gráfico en forma de taza $cup$ . Como ejemplo, la desigualdad de Jensen se refiere a una desigualdad que implica una función convexa o convex-(down).

Propiedades

Muchas propiedades de funciones convexas tienen la misma formulación simple para funciones de muchas variables que para funciones de una variable. Vea a continuación las propiedades para el caso de muchas variables, ya que algunas de ellas no se enumeran para funciones de una variable.

Funciones de una variable

Suppose $f$ es una función de una variable real definida en un intervalo, y dejar ${displaystyle R(x_{1},x_{2})={frac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}}$ (nota que ${displaystyle R(x_{1},x_{2})}$ es la pendiente de la línea púrpura en el dibujo anterior; la función $R$ es simétrico en ${displaystyle (x_{1},x_{2}),}$ significa que $R$ no cambia al cambiar $x_{1}$ y $x_{2}$ ). $f$ es convex si y sólo si ${displaystyle R(x_{1},x_{2})}$ es monotonicamente no disminuyendo ${displaystyle x_{1},}$ para cada fijo $x_{2}$ (o viceversa). Esta caracterización de la convexidad es bastante útil para probar los siguientes resultados.
Una función convexa $f$ de una variable real definida en algún intervalo abierto $C$ continuo ${displaystyle C.}$ $f$ Admite los derivados izquierdo y derecho, y estos son monotonicamente no disminuyendo. En consecuencia, $f$ es diferente en absoluto, pero en la mayoría de los puntos contables, el conjunto en el que $f$ no es diferente puede sin embargo todavía ser denso. Si $C$ está cerrado, entonces $f$ puede no ser continuo en los puntos finales de $C$ (un ejemplo se muestra en la sección ejemplos).
Una función diferencial de una variable es convex en un intervalo si y sólo si su derivado es monotonicamente no disminuye en ese intervalo. Si una función es diferente y convexa, entonces también es continuamente diferente.
Una función diferenciable de una variable es convex en un intervalo si y sólo si su gráfico se encuentra por encima de todos sus tangentes: ${displaystyle f(x)geq f(y)+f'(y)(x-y)}$ para todos $x$ y $y$ en el intervalo.
Una función dos veces diferente de una variable es convex en un intervalo si y sólo si su segundo derivado no es negativo allí; esto da una prueba práctica para la convexidad. Visualmente, una función convexa dos veces diferente "curves up", sin ninguna curva de la otra manera (puntos de inflexión). Si su segundo derivado es positivo en todos los puntos entonces la función es estrictamente convexa, pero el converso no sostiene. Por ejemplo, el segundo derivado de f()x)=x4{displaystyle f(x)=x^{4} ${displaystyle f(x)=x^{4}}$ es f.()x)=12x2{displaystyle f''(x)=12x^{2} ${displaystyle f''(x)=12x^{2}}$ , que es cero para x=0,{displaystyle x=0,} ${displaystyle x=0,}$ pero x4{displaystyle x^{4} $x^4$ Es estrictamente convexo.
- Esta propiedad y la propiedad anterior en términos de "...su derivado es monotonicamente no-creciente..." no son iguales ya que si $f''$ es no negativo en un intervalo $X$ entonces $f'$ es monotonicamente no disminuyendo $X$ mientras su contrario no es cierto, por ejemplo, $f'$ es monotonicamente no disminuyendo $X$ mientras que su derivados $f''$ no se define en algunos puntos $X$ .
Si $f$ es una función convexa de una variable real, y ${displaystyle f(0)leq 0}$ , entonces $f$ es superadditivo en los reales positivos, es decir ${displaystyle f(a+b)geq f(a)+f(b)}$ para números reales positivos $a$ y $b$ .

Prueba

Desde $f$ es convex, utilizando una de las definiciones de función convex arriba y dejando ${displaystyle x_{2}=0,}$ sigue que para siempre ${displaystyle 0leq tleq 1,}$

{displaystyle f(tx_{1})=f(tx_{1}+(1-t)cdot 0)leq tf(x_{1})+(1-t)f(0)leq tf(x_{1})rightarrow f(tx_{1})leq tf(x_{1}).}

De esto sigue que

{displaystyle f(a)+f(b)=fleft((a+b){frac {a}{a+b}}right)+fleft((a+b){frac {b}{a+b}}right)leq {frac {a}{a+b}}f(a+b)+{frac {b}{a+b}}f(a+b)=f(a+b)rightarrow f(a)+f(b)leq f(a+b).}

Una función es el punto medio convexo en un intervalo $C$ si para todos ${displaystyle x_{1},x_{2}in C}$ ${displaystyle fleft({frac {x_{1}+x_{2}}{2}}right)leq {frac {f(x_{1})+f(x_{2})}{2}}.}$ Esta condición es un poco más débil que la convexidad. Por ejemplo, una función medible Lebesgue de valor real que es midpoint-convex es convex: este es un teorema de Sierpinski. En particular, una función continua que es convex de punto medio será convexa.

Funciones de varias variables

Una función ${displaystyle f:Xto [-inftyinfty ]}$ valorado en los números reales extendidos ${displaystyle [-inftyinfty ]=mathbb {R} cup {pm infty }}$ es convex si y sólo si su epígrafe ${displaystyle {(x,r)in Xtimes mathbb {R} ~:~rgeq f(x)}}$ es un conjunto convexo.
Una función diferente $f$ definido en un dominio convex es convex si y sólo si ${displaystyle f(x)geq f(y)+nabla f(y)^{T}cdot (x-y)}$ para todos $x,y$ en el dominio.
Una función dos veces diferenciable de varias variables es convex en un conjunto convex si y sólo si su matriz hesiana de segundos derivados parciales es semidefinido positivo en el interior del conjunto convex.
Para una función convexa $f,$ los subgrupos $<math alttext="{displaystyle {x:f(x) {}x:f()x).a}{displaystyle {x:f(x)traducidoa} <img alt="{displaystyle {x:f(x)$ y ${displaystyle {x:f(x)leq a}}$ con ${displaystyle ain mathbb {R} }$ son conjuntos de convex. Una función que satisface esta propiedad se llama función quasiconvex y puede no ser una función convexa.
En consecuencia, el conjunto de minimisers globales de una función convexa $f$ es un conjunto convexo: ${displaystyle {operatorname {argmin} },f}$ - Convex.
Cualquier mínimo local de una función convexa es también un mínimo global. A estrictamente estricta la función convex tendrá al máximo un mínimo global.
La desigualdad de Jensen se aplica a cada función convexa $f$ . Si $X$ es una variable aleatoria que toma valores en el dominio de $f,$ entonces ${displaystyle operatorname {E} (f(X))geq f(operatorname {E} (X)),}$ Donde $operatorname {E}$ denota la expectativa matemática. De hecho, las funciones convexas son exactamente las que satisfacen la hipótesis de la desigualdad de Jensen.
Una función homogénea de primer orden de dos variables positivas $x$ y $y,$ (es decir, una función satisfactoria ${displaystyle f(ax,ay)=af(x,y)}$ para todos los reales positivos $0}" xmlns="http://www.w3.org/1998/Math/MathML">a,x,Sí.■0{displaystyle a,x,y confía0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a113e6453dddaaf46770c82343faaef84d70ad46" style="vertical-align: -0.671ex; width:10.044ex; height:2.509ex;"/>$ ) que es convex en una variable debe ser convex en la otra variable.

Operaciones que preservan la convexidad

$-f$ es cóncavo si y sólo si $f$ es convex.
Si $r$ es cualquier número real entonces ${displaystyle r+f}$ es convex si y sólo si $f$ es convex.
Sumas ponderadas no negativas:
- si ${displaystyle w_{1},ldotsw_{n}geq 0}$ y ${displaystyle f_{1},ldotsf_{n}}$ son todos convexos, entonces lo es ${displaystyle w_{1}f_{1}+cdots +w_{n}f_{n}.}$ En particular, la suma de dos funciones convexas es convexa.
- esta propiedad se extiende a sumas infinitas, integrales y valores esperados también (siempre que existan).
Elementwise maximum: Deja {}fi}i▪ ▪ I{displaystyle {f} {f} {f} {f} {f}\f}\\f}\\\f}\\f}\\\\\\\\f}\\\\\\\\\\f}\\\f}\\\\\f}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ I} ${displaystyle {f_{i}}_{iin I}}$ ser una colección de funciones convexas. Entonces... g()x)=Supi▪ ▪ Ifi()x){displaystyle g(x)=sup nolimits _{iin I}f_{i}(x)} ${displaystyle g(x)=sup nolimits _{iin I}f_{i}(x)}$ es convex. El dominio de g()x){displaystyle g(x)} $g(x)$ es la colección de puntos donde la expresión es finita. Casos especiales importantes:
- Si ${displaystyle f_{1},ldotsf_{n}}$ son funciones convex entonces, así es ${displaystyle g(x)=max left{f_{1}(x),ldotsf_{n}(x)right}.}$
- Teorema de Danskin: Si $f(x,y)$ es convexo en $x$ entonces ${displaystyle g(x)=sup nolimits _{yin C}f(x,y)}$ es convexo en $x$ incluso si $C$ no es un conjunto convexo.
Composición:
- Si $f$ y $g$ son funciones convexas y $g$ no está disminuyendo sobre un dominio univariado, entonces $h(x)=g(f(x))$ es convex. Por ejemplo, si $f$ es convexo, entonces lo es $e^{f(x)}$ porque $e^{x}$ es convexo y aumenta monotonicamente.
- Si $f$ es cóncavo y $g$ es convexa y no aumenta sobre un dominio univariado, entonces $h(x)=g(f(x))$ es convex.
- La convexidad es invariante bajo los mapas de afinidad: es decir, si $f$ es convex con dominio $D_{f}subseteq mathbf {R} ^{m}$ , entonces lo es $g(x)=f(Ax+b)$ , donde ${displaystyle Ain mathbf {R} ^{mtimes n},bin mathbf {R} ^{m}}$ con dominio ${displaystyle D_{g}subseteq mathbf {R} ^{n}.}$
Minimización: Si $f(x,y)$ es convexo en $(x,y)$ entonces ${displaystyle g(x)=inf nolimits _{yin C}f(x,y)}$ es convexo en $x,$ siempre que $C$ es un conjunto convexo y que ${displaystyle g(x)neq -infty.}$
Si $f$ es convexa, entonces su perspectiva ${displaystyle g(x,t)=tfleft({tfrac {x}{t}}right)}$ con dominio $0right}}" xmlns="http://www.w3.org/1998/Math/MathML">{}()x,t):xt▪ ▪ Dom⁡ ⁡ ()f),t■0}{displaystyle left{(x,t):{tfrac {x}in operatorname {Dom} (f),t Conf0right}0right}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/135bdb99003cc797f3b28fc26100a09041c0b2e4" style="vertical-align: -1.171ex; width:28.373ex; height:3.343ex;"/>$ es convex.
Vamos $X$ ser un espacio vectorial. ${displaystyle f:Xto mathbf {R} }$ es convex y satisfies ${displaystyle f(0)leq 0}$ si ${displaystyle f(ax+by)leq af(x)+bf(y)}$ para cualquier $x, y in X$ y cualquier número real no negativo $a,b$ que satisfacen ${displaystyle a+bleq 1.}$

Funciones fuertemente convexas

El concepto de convexidad fuerte amplía y parametriza la noción de convexidad estricta. Una función fuertemente convexa también es estrictamente convexa, pero no viceversa.

Una función diferente $f$ se llama fuerte convexo con parámetro $0}" xmlns="http://www.w3.org/1998/Math/MathML">m■0{displaystyle m confía0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/501173910e6da8425b4e9d44a4e8643620bc2464" style="vertical-align: -0.338ex; width:6.301ex; height:2.176ex;"/>$ si la siguiente desigualdad tiene para todos los puntos $x,y$ en su dominio:

{displaystyle (nabla f(x)-nabla f(y))^{T}(x-y)geq m|x-y|_{2}^{2}}

{displaystyle langle nabla f(x)-nabla f(y),x-yrangle geq m|x-y|^{2}}

{displaystyle langle cdotcdot rangle }

|cdot |

Una condición equivalente es la siguiente:

{displaystyle f(y)geq f(x)+nabla f(x)^{T}(y-x)+{frac {m}{2}}|y-x|_{2}^{2}}

No es necesario que una función sea diferente para ser fuertemente convexa. Una tercera definición para una función fuertemente convexa, con parámetro $m,$ es eso, para todos $x,y$ en el dominio y $tin [0,1],$

{displaystyle f(tx+(1-t)y)leq tf(x)+(1-t)f(y)-{frac {1}{2}}mt(1-t)|x-y|_{2}^{2}}

Note que esta definición se acerca a la definición de convexidad estricta como ${displaystyle mto 0,}$ y es idéntica a la definición de una función convexa cuando ${displaystyle m=0.}$ A pesar de esto, existen funciones que son estrictamente convexas pero no son fuertemente convexas para cualquier $0}" xmlns="http://www.w3.org/1998/Math/MathML">m■0{displaystyle m confía0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/501173910e6da8425b4e9d44a4e8643620bc2464" style="vertical-align: -0.338ex; width:6.301ex; height:2.176ex;"/>$ (véase el ejemplo infra).

Si la función $f$ es dos veces continuamente diferenciable, entonces es fuertemente convexo con parámetro $m$ si ${displaystyle nabla ^{2}f(x)succeq mI}$ para todos $x$ en el dominio, donde $I$ es la identidad y $nabla ^{2}f$ es la matriz hesiana, y la desigualdad $succeq$ significa que ${displaystyle nabla ^{2}f(x)-mI}$ es semi-definido positivo. Esto equivale a exigir que el eigenvalo mínimo de $nabla ^{2}f(x)$ al menos $m$ para todos $x.$ Si el dominio es sólo la línea real, entonces $nabla ^{2}f(x)$ es sólo el segundo derivado ${displaystyle f''(x),}$ así que la condición se convierte $f''(x)geq m$ . Si $m=0$ entonces esto significa que el Hessian es semidefinido positivo (o si el dominio es la línea real, significa que $f''(x)geq 0$ ), lo que implica la función es convex, y tal vez estrictamente convex, pero no fuertemente convex.

Asumiendo que la función es dos veces continuamente diferenciable, se puede demostrar que el límite inferior de $nabla ^{2}f(x)$ implica que es fuertemente convexo. Usando el teorema de Taylor existe

{displaystyle zin {tx+(1-t)y:tin [0,1]}}

{displaystyle f(y)=f(x)+nabla f(x)^{T}(y-x)+{frac {1}{2}}(y-x)^{T}nabla ^{2}f(z)(y-x)}

{displaystyle (y-x)^{T}nabla ^{2}f(z)(y-x)geq m(y-x)^{T}(y-x)}

Una función $f$ es fuertemente convexo con parámetro m si y sólo si la función

{displaystyle xmapsto f(x)-{frac {m}{2}}|x|^{2}}

La distinción entre convex, estrictamente convex, y fuertemente convex puede ser sutil a primera vista. Si $f$ es dos veces continuamente diferenciable y el dominio es la línea real, entonces podemos caracterizarlo como sigue:

$f$ convex si y sólo si $f''(x)geq 0$ para todos $x.$
$f$ estrictamente convex si $0}" xmlns="http://www.w3.org/1998/Math/MathML">f.()x)■0{displaystyle f''(x)}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5242d6e86d1b65eddd578b3a58f08635e32361cf" style="vertical-align: -0.838ex; width:9.858ex; height:3.009ex;"/>$ para todos $x$ (nota: esto es suficiente, pero no necesario).
$f$ fuertemente convex si y sólo si $0}" xmlns="http://www.w3.org/1998/Math/MathML">f.()x)≥ ≥ m■0{displaystyle f''(x)geq m título0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8cfbc2b894ed64434dfc61fa9e2f666db1addc06" style="vertical-align: -0.838ex; width:14.996ex; height:3.009ex;"/>$ para todos $x.$

Por ejemplo, vamos $f$ ser estrictamente convexo, y supone que hay una secuencia de puntos $(x_{n})$ tales que ${displaystyle f''(x_{n})={tfrac {1}{n}}}$ . Aunque $0}" xmlns="http://www.w3.org/1998/Math/MathML">f.()xn)■0{displaystyle f''(x_{n}]0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/818a4e7cd82954d80cfc81c2af7de8ee3294f16f" style="vertical-align: -0.838ex; width:11.076ex; height:3.009ex;"/>$ , la función no es fuertemente convex porque $f''(x)$ será arbitrariamente pequeño.

Una función doblemente diferenciable $f$ en un dominio compacto $X$ que satisfice $0}" xmlns="http://www.w3.org/1998/Math/MathML">f.()x)■0{displaystyle f''(x)}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5242d6e86d1b65eddd578b3a58f08635e32361cf" style="vertical-align: -0.838ex; width:9.858ex; height:3.009ex;"/>$ para todos $xin X$ es fuertemente convexa. La prueba de esta declaración se deriva del teorema de valor extremo, que afirma que una función continua en un conjunto compacto tiene un máximo y mínimo.

En general, es más fácil trabajar con funciones fuertemente convexas que con funciones convexas o estrictamente convexas, ya que son una clase más pequeña. Al igual que las funciones estrictamente convexas, las funciones fuertemente convexas tienen mínimos únicos en conjuntos compactos.

Funciones uniformemente convexas

Una función convexa uniforme, con módulo $phi$ , es una función $f$ que, para todos $x,y$ en el dominio y ${displaystyle tin [0,1],}$ satisfizo

{displaystyle f(tx+(1-t)y)leq tf(x)+(1-t)f(y)-t(1-t)phi (|x-y|)}

phi

{displaystyle phi (alpha)={tfrac {m}{2}}alpha ^{2}}

Vale la pena señalar que algunos autores requieren el módulo $phi$ para ser una función creciente, pero esta condición no es requerida por todos los autores.

Ejemplos

Funciones de una variable

La función $f(x)=x^{2}$ tiene $0}" xmlns="http://www.w3.org/1998/Math/MathML">f.()x)=2■0{displaystyle f''(x)=2 título0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8ed14395c44bd421b25a6a705f582ff6f9657d71" style="vertical-align: -0.838ex; width:14.119ex; height:3.009ex;"/>$ Así que $f$ es una función convexa. También es fuertemente convexa (y por lo tanto estrictamente convexa también), con fuerte convexidad constante 2.
La función $f(x)=x^{4}$ tiene ${displaystyle f''(x)=12x^{2}geq 0}$ Así que $f$ es una función convexa. Es estrictamente convexo, aunque el segundo derivado no es estrictamente positivo en todos los puntos. No es fuertemente convexo.
Función de valor absoluto $f(x)=|x|$ es convex (como se refleja en la desigualdad del triángulo), aunque no tiene un derivado en el punto $x=0.$ No es estrictamente convexo.
La función $f(x)=|x|^{p}$ para ${displaystyle pgeq 1}$ es convex.
La función exponencial $f(x)=e^{x}$ es convex. También es estrictamente convexo, ya que $0}" xmlns="http://www.w3.org/1998/Math/MathML">f.()x)=ex■0{displaystyle f''(x)=e^{x} {0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/2c38241c9795ee99d79084d6eacc5cc021cf5853" style="vertical-align: -0.838ex; width:15.212ex; height:3.009ex;"/>$ , pero no es fuertemente convexo ya que el segundo derivado puede ser arbitrariamente cercano a cero. Más generalmente, la función $g(x)=e^{f(x)}$ es logaritmically convex si $f$ es una función convexa. El término "superconvex" a veces se utiliza en su lugar.
La función $f$ con dominio [0,1] definido por ${displaystyle f(0)=f(1)=1,f(x)=0}$ para $<math alttext="{displaystyle 0<x0.x.1{displaystyle 0 madex 0} <img alt="0 < x$ es convexo; es continuo en el intervalo abierto ${displaystyle (0,1),}$ pero no continuo en 0 y 1.
La función $x^{3}$ tiene segundo derivado ${displaystyle 6x}$ ; por lo tanto es convexo en el conjunto donde $xgeq 0$ y cóncava en el conjunto donde ${displaystyle xleq 0.}$
Ejemplos de funciones que aumentan monotonicamente pero no convexas incluyen $f(x)={sqrt {x}}$ y ${displaystyle g(x)=log x}$ .
Ejemplos de funciones que son convexas pero no aumentan monotonicamente incluyen ${displaystyle h(x)=x^{2}}$ y $k(x)=-x$ .
La función ${displaystyle f(x)={tfrac {1}{x}}}$ tiene ${displaystyle f''(x)={tfrac {2}{x^{3}}}}$ que es mayor que 0 si $0}" xmlns="http://www.w3.org/1998/Math/MathML">x■0{displaystyle x confianza0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/80d24be5f0eb4a9173da6038badc8659546021d0" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/>$ Así que... $f(x)$ es convexo en el intervalo $(0,infty)$ . Es cóncava en el intervalo ${displaystyle (-infty0)}$ .
La función ${displaystyle f(x)={tfrac {1}{x^{2}}}}$ con ${displaystyle f(0)=infty }$ , es convexo en el intervalo $(0,infty)$ y convexo en el intervalo ${displaystyle (-infty0)}$ , pero no convexo en el intervalo $(-inftyinfty)$ , debido a la singularidad en $x=0.$

Funciones de n variables

LogSum La función Exp, también llamada función softmax, es una función convexa.
La función ${displaystyle -log det(X)}$ en el dominio de matrices-definidas positivas es convex.
Cada transformación lineal de valor real es convexa pero no estrictamente convexa, ya que si $f$ es lineal, entonces ${displaystyle f(a+b)=f(a)+f(b)}$ . Esta declaración también sostiene si reemplazamos "convex" por "concave".
Cada función afina real valorada, es decir, cada función de la forma ${displaystyle f(x)=a^{T}x+b,}$ es simultáneamente convex y concave.
Cada norma es una función convexa, por la desigualdad del triángulo y la homogeneidad positiva.
El radio espectral de una matriz no negativa es una función convexa de sus elementos diagonales.

Contenido relacionado

Más resultados...