Frecuencia de corte

Función de transferencia de Magnitud de un filtro de bandpass con menor frecuencia de corte 3 dB f₁ frecuencia de corte superior 3 dB f₂

A Bode plot of the Butterworth filter's frequency response, with corner frequency label

En física e ingeniería eléctrica, una frecuencia de corte, frecuencia de esquina o frecuencia de ruptura es un límite en el sistema Respuesta de frecuencia en la que la energía que fluye a través del sistema comienza a reducirse (atenuarse o reflejarse) en lugar de pasar.

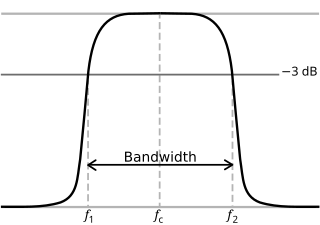
Por lo general, en sistemas electrónicos como filtros y canales de comunicación, la frecuencia de corte se aplica a un borde en una característica de paso bajo, paso alto, paso de banda o supresión de banda: una frecuencia que caracteriza un límite entre una banda de paso y una banda suprimida. A veces se toma como el punto en la respuesta del filtro donde se encuentran una banda de transición y una banda de paso, por ejemplo, según lo define un punto de media potencia (una frecuencia para la cual la salida del circuito es −3 dB del valor nominal de la banda de paso). Alternativamente, una frecuencia de esquina de banda suprimida puede especificarse como un punto donde se encuentran una banda de transición y una banda suprimida: una frecuencia para la cual la atenuación es mayor que la atenuación de la banda suprimida requerida, que por ejemplo puede ser 30 dB o 100 dB.

En el caso de una guía de ondas o una antena, las frecuencias de corte corresponden a las longitudes de onda de corte inferior y superior.

Electrónica

En electrónica, frecuencia de corte o frecuencia de esquina es la frecuencia por encima o por debajo que la salida de potencia de un circuito, como una línea, amplificador o filtro electrónico ha caído a una proporción determinada de la potencia en la banda de paso. Con más frecuencia esta proporción es la mitad de la potencia de la banda, también conocida como el punto 3 dB, ya que una caída de 3 dB corresponde aproximadamente a la mitad de la potencia. Como una relación de tensión es una caída a 1/2.. 0.707{textstyle {sqrt {1/2}approx 0.707} de la tensión de banda. Otras ratios además del punto 3 dB también pueden ser relevantes, por ejemplo véase § Chebyshev filtros abajo. Lejos de la frecuencia de corte en la banda de transición, la tasa de aumento de atenuación (roll-off) con logaritmo de frecuencia es asintotica a una constante. Para una red de primer orden, el lanzamiento es de 20 dB por decenio (-6 dB por octava).

Ejemplo de función de transferencia unipolar

La función de transferencia para el filtro de paso bajo más simple,

H()s)=11+α α s,{displaystyle H(s)={1}{1+alpha s}}

SilencioH()j⋅ ⋅ )Silencio=Silencio11+α α j⋅ ⋅ Silencio=11+α α 2⋅ ⋅ 2.{displaystyle left WordPressH(jomega)right sobre la vida=lefttención{frac {1}{1+alpha jomega {fnMicroc}{1+alpha ^{2}omega ^{2}}}}

En el corte

SilencioH()j⋅ ⋅ c)Silencio=12=11+α α 2⋅ ⋅ c2.{displaystyle left WordPressH(jomega _{mathrm {c})right sobre la vida={frac {1}{sqrt {2}={sqrt {fnMic} {fnK}}= {fnMic} {fnK} {f} {fnK}}} {f}}} {fn}}} {fnf}} {fnfnf}}}}} {fnfnfnfnf}}}}}}}}}}}}}}\\\fnfn\\\fnfnfnfn\fnfnfnfnfnfnfn\\fnfn\fnfnfn\fnfn\fnfn\fnfnfnfnfnfnfnfnfnfnfnfnfn\fn\\\fn {1}{1+alpha ^{2}omega _{mathrm {c}} {}}}}}

Por lo tanto, la frecuencia de corte viene dada por

⋅ ⋅ c=1α α .{displaystyle omega _{mathrm {c} }={frac {1}{alpha }}

Donde s es la variable del plano s, ω es angular frecuencia y j es la unidad imaginaria.

Filtros Chebyshev

A veces, otras proporciones son más convenientes que el punto de 3 dB. Por ejemplo, en el caso del filtro Chebyshev, es habitual definir la frecuencia de corte como el punto después del último pico en la respuesta de frecuencia en el que el nivel ha caído al valor de diseño de la ondulación de la banda de paso. El diseñador puede establecer la cantidad de ondulación en esta clase de filtro en cualquier valor deseado, por lo tanto, la relación utilizada podría ser cualquier valor.

Radiocomunicaciones

En la comunicación por radio, la comunicación por ondas celestes es una técnica en la que las ondas de radio se transmiten en ángulo hacia el cielo y se reflejan de regreso a la Tierra mediante capas de partículas cargadas en la ionosfera. En este contexto, el término frecuencia de corte se refiere a la frecuencia máxima utilizable, la frecuencia por encima de la cual una onda de radio no se refleja en la ionosfera en el ángulo de incidencia requerido para la transmisión entre dos puntos específicos por reflexión desde el capa.

Guías de onda

La frecuencia de corte de una guía de ondas electromagnética es la frecuencia más baja para la que se propagará un modo en ella. En fibra óptica, es más común considerar la longitud de onda de corte, la longitud de onda máxima que se propagará en una fibra óptica o guía de ondas. La frecuencia de corte se encuentra con la ecuación característica de la ecuación de Helmholtz para ondas electromagnéticas, que se deriva de la ecuación de onda electromagnética estableciendo el número de onda longitudinal igual a cero y resolviendo la frecuencia. Por lo tanto, cualquier frecuencia de excitación más baja que la frecuencia de corte se atenuará en lugar de propagarse. La siguiente derivación asume paredes sin pérdidas. El valor de c, la velocidad de la luz, debe tomarse como la velocidad de grupo de la luz en cualquier material que llene la guía de ondas.

Para una guía de ondas rectangular, la frecuencia de corte es

⋅ ⋅ c=c()nπ π a)2+()mπ π b)2,{displaystyle omega ¿Por qué? - Sí.

m,n≥ ≥ 0{displaystyle m,ngeq 0}

a{displaystyle a}

b{displaystyle b}

m,n≥ ≥ 0{displaystyle m,ngeq 0}

m=n=0{displaystyle m=n=0}

m,n≥ ≥ 1{displaystyle m,ngeq 1}

La frecuencia de corte del modo TM₀₁ (el siguiente más alto desde el modo dominante TE₁₁) en una guía de ondas de sección transversal circular (el modo magnético transversal sin dependencia angular y dependencia radial más baja) viene dada por

⋅ ⋅ c=cχ χ 01r=c2.4048r,{displaystyle omega ¿Por qué? {fnMicrosoft Sans Serif} ¿Qué?

r{displaystyle r}

χ χ 01{displaystyle chi _{01}}

J0()r){displaystyle J_{0}(r)}

La frecuencia de corte del modo dominante TE₁₁ viene dada por

⋅ ⋅ c=cχ χ 11r=c1.8412r{displaystyle omega ¿Por qué? {fnMicrosoft Sans Serif} - ¿Qué?

Sin embargo, la frecuencia de corte del modo dominante se puede reducir mediante la introducción de un deflector dentro de la guía de ondas de sección transversal circular. Para una fibra óptica monomodo, la longitud de onda de corte es la longitud de onda en la que la frecuencia normalizada es aproximadamente igual a 2,405.

Análisis matemático

El punto de partida es la ecuación de onda (que se deriva de las ecuaciones de Maxwell),

()Silencio Silencio 2− − 1c2∂ ∂ 2∂ ∂ t2)↑ ↑ ()r,t)=0,{displaystyle left(nabla) ¿Qué?

↑ ↑ ()x,Sí.,z,t)=↑ ↑ ()x,Sí.,z)ei⋅ ⋅ t.{displaystyle psi (x,y,z,t)=psi (x,y,z)e^{iomega t}

()Silencio Silencio 2+⋅ ⋅ 2c2)↑ ↑ ()x,Sí.,z)=0.{displaystyle left(nabla) ^{2}+{frac {omega Bien.

↑ ↑ {displaystyle psi }

El "longitudinal" la derivada en el laplaciano se puede reducir aún más considerando solo funciones de la forma

↑ ↑ ()x,Sí.,z,t)=↑ ↑ ()x,Sí.)ei()⋅ ⋅ t− − kzz),{displaystyle psi (x,y,z,t)=psi (x,y)e^{ileft(omega t-k_{z}zright)}}

kz{displaystyle k_{z}

()Silencio Silencio T2− − kz2+⋅ ⋅ 2c2)↑ ↑ ()x,Sí.,z)=0,{displaystyle left(nabla) ¿Qué? Bien.

↑ ↑ ()x,Sí.,z,t)=↑ ↑ 0ei()⋅ ⋅ t− − kzz− − kxx− − kSí.Sí.).{displaystyle psi (x,y,z,t)=psi ¿Por qué?.

⋅ ⋅ 2c2=kx2+kSí.2+kz2{displaystyle {frac {omega ¿Qué?

kx=nπ π a,{displaystyle ¿Qué?

kSí.=mπ π b,{displaystyle k_{y}={frac {mpi } {b},}

⋅ ⋅ 2c2=()nπ π a)2+()mπ π b)2+kz2,{displaystyle {frac {omega ¿Qué? ¿Qué?

⋅ ⋅ c{displaystyle omega _{c}

kz{displaystyle k_{z}

⋅ ⋅ c=c()nπ π a)2+()mπ π b)2{displaystyle omega ¿Por qué? - Sí.