Forma indeterminada

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Expresión en análisis matemático

En cálculo y otras ramas del análisis matemático, cuando se toma el límite de la suma, diferencia, producto, cociente o potencia de dos funciones, a menudo es posible simplemente sumar, restar, multiplicar, dividir o exponenciar las correspondientes. límites de estas dos funciones respectivamente. Sin embargo, hay ocasiones en las que no está claro cuál debería ser la suma, diferencia, producto o potencia de estos dos límites. Por ejemplo, no está claro cómo deberían evaluarse las siguientes expresiones:

{displaystyle {frac {0}{0}},~{frac {infty }{infty }},~0times infty~infty -infty~0^{0},~1^{infty },{text{ and }}infty ^{0}.}

Estas siete expresiones se conocen como formas indeterminadas. Más específicamente, tales expresiones se obtienen aplicando ingenuamente el teorema algebraico del límite para evaluar el límite de la operación aritmética correspondiente de dos funciones, sin embargo, hay ejemplos de pares de funciones que después de ser operadas convergen a 0, convergen a otro valor finito, divergen hasta el infinito o simplemente divergen. Esta incapacidad para decidir cuál debería ser el límite explica por qué estas formas se consideran indeterminadas. Un límite confirmado como infinito no es indeterminado ya que se ha determinado que tiene un valor específico (infinito). El término fue introducido originalmente por Moigno, alumno de Cauchy, a mediados del siglo XIX.

El ejemplo más común de una forma indeterminada es el cociente de dos funciones cada una de las cuales converge a cero. Esta forma indeterminada es denotada por $0/0$ . Por ejemplo, como $x$ enfoques ${displaystyle 0~}$ , las ratios ${displaystyle x/x^{3}}$ , ${displaystyle x/x}$ , y ${displaystyle x^{2}/x}$ ir a $infty$ , $1$ , y ${displaystyle 0~}$ respectivamente. En cada caso, si se sustituyen los límites del numerador y el denominador, la expresión resultante es $0/0$ , que es indeterminado. En este sentido, $0/0$ puede asumir los valores ${displaystyle 0~}$ , $1$ , o $infty$ , por opciones apropiadas de funciones para poner en el numerador y denominador. Un par de funciones para las cuales el límite es cualquier valor dado en particular se puede encontrar de hecho. Aún más sorprendente, tal vez, el cociente de las dos funciones puede de hecho divergir, y no simplemente divergir al infinito. Por ejemplo, ${displaystyle xsin(1/x)/x}$ .

Así que el hecho de que dos funciones $f(x)$ y $g(x)$ converger ${displaystyle 0~}$ como $x$ algunos puntos límite $c$ es insuficiente para determinar el límite

{displaystyle lim _{xto c}{frac {f(x)}{g(x)}}.}

Una expresión que surge por maneras distintas de aplicar el termorema de límite algebraico puede tener la misma forma de una forma indeterminada. Sin embargo, no es apropiado llamar una expresión "forma indeterminada" si la expresión se hace fuera del contexto de determinar límites. Por ejemplo, $0/0$ que surge de la sustitución ${displaystyle 0~}$ para $x$ en la ecuación ${displaystyle f(x)=|x|/(|x-1|-1)}$ no es una forma indeterminada ya que esta expresión no se hace en la determinación de un límite (de hecho, no está definida como división por cero). Otro ejemplo es la expresión $0^{0}$ . Si esta expresión queda indefinida, o se define a igual $1$ , depende del campo de aplicación y puede variar entre autores. Para más, vea el artículo Zero al poder de cero. Note que ${displaystyle 0^{infty }}$ y otras expresiones que implican el infinito no son formas indeterminadas.

Algunos ejemplos y no ejemplos

Forma indeterminada 0/0

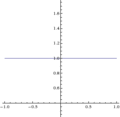
Fig. 1: Sí. = x/x
Fig. 2: Sí. = x²/x
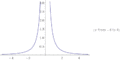
Fig. 3: Sí. = pecadox/x
Fig. 4: Sí. = x −49/√x 7 - (por x = 49)
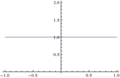
Fig. 5: Sí. = ax/x Donde a = 2
Fig. 6: Sí. = x/x³

La forma indeterminada $0/0$ es particularmente común en el cálculo, porque a menudo surge en la evaluación de los derivados utilizando su definición en términos de límite.

Como se mencionó anteriormente,

{displaystyle lim _{xto 0}{frac {x}{x}}=1,qquad }

(ver fig. 1)

mientras

{displaystyle lim _{xto 0}{frac {x^{2}}{x}}=0,qquad }

(ver fig. 2)

Esto es suficiente para demostrar que $0/0$ es una forma indeterminada. Otros ejemplos con esta forma indeterminada incluyen

{displaystyle lim _{xto 0}{frac {sin(x)}{x}}=1,qquad }

(ver fig. 3)

{displaystyle lim _{xto 49}{frac {x-49}{{sqrt {x}},-7}}=14,qquad }

(ver fig. 4)

Sustitución directa del número que $x$ enfoques en cualquiera de estas expresiones muestra que estos son ejemplos corresponden a la forma indeterminada $0/0$ , pero estos límites pueden asumir muchos valores diferentes. Cualquier valor deseado $a$ se puede obtener para esta forma indeterminada como sigue:

{displaystyle lim _{xto 0}{frac {ax}{x}}=a.qquad }

(ver fig. 5)

El valor $infty$ también se puede obtener (en el sentido de la divergencia al infinito):

{displaystyle lim _{xto 0}{frac {x}{x^{3}}}=infty.qquad }

(ver fig. 6)

Forma indeterminada 00

Fig. 7: Sí. = x⁰
Fig. 8: Sí. = 0^x

Los siguientes límites ilustran que la expresión $0^{0}$ es una forma indeterminada:

{displaystyle lim _{xto 0^{+}}x^{0}=1,qquad }

(ver fig. 7)

{displaystyle lim _{xto 0^{+}}0^{x}=0.qquad }

(ver fig. 8)

Así, en general, sabiendo que ${displaystyle textstyle lim _{xto c}f(x);=;0}$ y ${displaystyle textstyle lim _{xto c}g(x);=;0}$ no es suficiente para evaluar el límite

lim_{x to c} f(x)^{g(x)}.

Si las funciones $f$ y $g$ son analytic en $c$ , y $f$ es positivo $x$ suficientemente cerca (pero no igual) a $c$ , entonces el límite $f(x)^{{g(x)}}$ será $1$ . De lo contrario, utilice la transformación en la tabla siguiente para evaluar el límite.

Expresiones que no son formas indeterminadas

La expresión $1/0$ no se considera comúnmente como una forma indeterminada, porque si el límite $f/g$ existe entonces no hay ambigüedad en cuanto a su valor, ya que siempre se divierte. Específicamente, si $f$ enfoques $1$ y $g$ enfoques ${displaystyle 0~}$ , entonces $f$ y $g$ puede ser elegido para que:

$f/g$ enfoques $+infty$
$f/g$ enfoques $-infty$
El límite no existe.

En cada caso el valor absoluto ${displaystyle |f/g|}$ enfoques $+infty$ , y así el cociente $f/g$ debe divergir, en el sentido de los números reales extendidos (en el marco de la línea real proyectada, el límite es el infinito no firmado $infty$ en los tres casos). Del mismo modo, cualquier expresión de la forma ${displaystyle a/0}$ con $aneq 0$ (incluidas ${displaystyle a=+infty }$ y $a=-infty$ ) no es una forma indeterminada, ya que un cociente que da lugar a tal expresión siempre va a divergir.

La expresión ${displaystyle 0^{infty }}$ no es una forma indeterminada. La expresión ${displaystyle 0^{+infty }}$ obtenido del examen ${displaystyle lim _{xto c}f(x)^{g(x)}}$ da el límite ${displaystyle 0~}$ , siempre que $f(x)$ restos $x$ enfoques $c$ . La expresión ${displaystyle 0^{-infty }}$ es similar a $1/0$ ; si $0}" xmlns="http://www.w3.org/1998/Math/MathML">f()x)■0{displaystyle f(x)}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/af29e26aaac6c969d32c8afac1f33ae703f442c7" style="vertical-align: -0.838ex; width:8.678ex; height:2.843ex;"/>$ como $x$ enfoques $c$ , el límite sale como $+infty$ .

Para ver por qué, vamos ${displaystyle L=lim _{xto c}f(x)^{g(x)},}$ Donde ${displaystyle lim _{xto c}{f(x)}=0,}$ y ${displaystyle lim _{xto c}{g(x)}=infty.}$ Tomando el logaritmo natural de ambos lados y utilizando ${displaystyle lim _{xto c}ln {f(x)}=-infty}$ lo tenemos ${displaystyle ln L=lim _{xto c}({g(x)}times ln {f(x)})=infty times {-infty }=-infty}$ que significa que ${displaystyle L={e}^{-infty }=0.}$

Evaluación de formas indeterminadas

El adjetivo indeterminado no implica que el límite no existe, como muestran muchos de los ejemplos anteriores. En muchos casos, se puede utilizar la eliminación algebraica, la regla de L'Hôpital u otros métodos para manipular la expresión de modo que se pueda evaluar el límite.

Infinitésimo equivalente

Cuando dos variables $alpha$ y $beta$ converger a cero en el mismo punto límite y ${displaystyle textstyle lim {frac {beta }{alpha }}=1}$ , se llaman equivalente infinitesimal (equiv. ${displaystyle alpha sim beta }$ ).

Además, si las variables $alpha '$ y $beta '$ son tales $alpha sim alpha '$ y $beta sim beta '$ , entonces:

{displaystyle lim {frac {beta }{alpha }}=lim {frac {beta '}{alpha '}}}

Aquí hay una breve prueba:

Supongamos que hay dos infinitos equivalentes $alpha sim alpha '$ y $beta sim beta '$ .

lim {frac {beta }{alpha }}=lim {frac {beta beta 'alpha '}{beta 'alpha 'alpha }}=lim {frac {beta }{beta '}}lim {frac {alpha '}{alpha }}lim {frac {beta '}{alpha '}}=lim {frac {beta '}{alpha '}}

Para la evaluación de la forma indeterminada $0/0$ , uno puede hacer uso de los siguientes hechos sobre infinitesimales equivalentes (por ejemplo, ${displaystyle xsim sin x}$ si x se acerca a cero):

xsim sin x,

xsim arcsin x,

{displaystyle xsim sinh x,}

xsim tan x,

xsim arctan x,

xsim ln(1+x),

{displaystyle 1-cos xsim {frac {x^{2}}{2}},}

{displaystyle cosh x-1sim {frac {x^{2}}{2}},}

a^{x}-1sim xln a,

{displaystyle e^{x}-1sim x,}

(1+x)^{a}-1sim ax.

Por ejemplo:

{displaystyle {begin{aligned}lim _{xto 0}{frac {1}{x^{3}}}left[left({frac {2+cos x}{3}}right)^{x}-1right]&=lim _{xto 0}{frac {e^{xln {frac {2+cos x}{3}}}-1}{x^{3}}}\&=lim _{xto 0}{frac {1}{x^{2}}}ln {frac {2+cos x}{3}}\&=lim _{xto 0}{frac {1}{x^{2}}}ln left({frac {cos x-1}{3}}+1right)\&=lim _{xto 0}{frac {cos x-1}{3x^{2}}}\&=lim _{xto 0}-{frac {x^{2}}{6x^{2}}}\&=-{frac {1}{6}}end{aligned}}}

En la segunda igualdad, ${displaystyle e^{y}-1sim y}$ Donde ${displaystyle y=xln {2+cos x over 3}}$ como Sí. se acerca a 0 se utiliza, y ${displaystyle ysim ln {(1+y)}}$ Donde ${displaystyle y={{cos x-1} over 3}}$ se utiliza en la cuarta igualdad, y ${displaystyle 1-cos xsim {x^{2} over 2}}$ se utiliza en la quinta igualdad.

Did you mean:

L''Hôpital's rule

La regla de L'Hôpital es un método general para evaluar las formas indeterminadas $0/0$ y ${displaystyle infty /infty }$ . Esta regla establece que (en condiciones apropiadas)

{displaystyle lim _{xto c}{frac {f(x)}{g(x)}}=lim _{xto c}{frac {f'(x)}{g'(x)}},}

Donde $f'$ y $g'$ son los derivados de $f$ y $g$ . (Nota que esta regla hace no aplica a las expresiones ${displaystyle infty /0}$ , $1/0$ , y así sucesivamente, ya que estas expresiones no son formas indeterminadas.) Estos derivados permitirán realizar simplificación algebraica y eventualmente evaluar el límite.

Did you mean:

'Hôpital's rule can also be applied to other indeterminate forms, using first an appropriate algebraic transformation. For example, to evaluate the form 0⁰:

{displaystyle ln lim _{xto c}f(x)^{g(x)}=lim _{xto c}{frac {ln f(x)}{1/g(x)}}.}

El lado derecho es de la forma ${displaystyle infty /infty }$ Así que la regla de L'Hôpital se aplica a ella. Tenga en cuenta que esta ecuación es válida (si el lado derecho es definido) porque el logaritmo natural (ln) es una función continua; es irrelevante lo bien-conformado $f$ y $g$ (o tal vez no) $f$ es asintoticamente positivo. (el dominio de los logaritmos es el conjunto de todos los números reales positivos.)

Aunque la regla de L'Hôpital se aplica a ambos $0/0$ y ${displaystyle infty /infty }$ , una de estas formas puede ser más útil que la otra en un caso particular (por la posibilidad de simplificación algebraica después). Uno puede cambiar entre estas formas transformando $f/g$ a ${displaystyle (1/g)/(1/f)}$ .

Lista de formas indeterminadas

La siguiente tabla enumera las formas indeterminadas más comunes y las transformaciones para aplicar la regla de L'Hôpital.

Indeterminate form	Conditions	Transformation to $0/0$	Transformation to ${displaystyle infty /infty }$
${displaystyle 0}$ / ${displaystyle 0}$	$lim_{x to c} f(x) = 0, lim_{x to c} g(x) = 0 !$	—	$lim_{x to c} frac{f(x)}{g(x)} = lim_{x to c} frac{1/g(x)}{1/f(x)} !$
$infty$ / $infty$	$lim_{x to c} f(x) = infty, lim_{x to c} g(x) = infty !$	$lim_{x to c} frac{f(x)}{g(x)} = lim_{x to c} frac{1/g(x)}{1/f(x)} !$	—
$0cdot infty$	$lim_{x to c} f(x) = 0, lim_{x to c} g(x) = infty !$	$lim_{x to c} f(x)g(x) = lim_{x to c} frac{f(x)}{1/g(x)} !$	$lim_{x to c} f(x)g(x) = lim_{x to c} frac{g(x)}{1/f(x)} !$
$infty -infty$	$lim_{x to c} f(x) = infty, lim_{x to c} g(x) = infty !$	$lim_{x to c} (f(x) - g(x)) = lim_{x to c} frac{1/g(x) - 1/f(x)}{1/(f(x)g(x))} !$	$lim_{x to c} (f(x) - g(x)) = ln lim_{x to c} frac{e^{f(x)}}{e^{g(x)}} !$
$0^{0}$	$lim_{x to c} f(x) = 0^+, lim_{x to c} g(x) = 0 !$	$lim_{x to c} f(x)^{g(x)} = exp lim_{x to c} frac{g(x)}{1/ln f(x)} !$	$lim_{x to c} f(x)^{g(x)} = exp lim_{x to c} frac{ln f(x)}{1/g(x)} !$
$1^{infty }$	$lim_{x to c} f(x) = 1, lim_{x to c} g(x) = infty !$	$lim_{x to c} f(x)^{g(x)} = exp lim_{x to c} frac{ln f(x)}{1/g(x)} !$	$lim_{x to c} f(x)^{g(x)} = exp lim_{x to c} frac{g(x)}{1/ln f(x)} !$
${displaystyle infty ^{0}}$	$lim_{x to c} f(x) = infty, lim_{x to c} g(x) = 0 !$	$lim_{x to c} f(x)^{g(x)} = exp lim_{x to c} frac{g(x)}{1/ln f(x)} !$	$lim_{x to c} f(x)^{g(x)} = exp lim_{x to c} frac{ln f(x)}{1/g(x)} !$

Contenido relacionado

Más resultados...