El dilema del prisionero
B A | B stays silencio | B traición |
|---|---|---|
| Una estancia silencio | -2 -2 | 0 -10 |
| A traición | -10 0 | -5 -5 |
El dilema del prisionero es un juego analizado en teoría de juegos. Es un experimento mental que desafía a dos agentes completamente racionales a un dilema: cooperar con su pareja para una recompensa mutua, o traicionar a su pareja ("defecto") por una recompensa individual.
Este dilema fue enmarcado originalmente por Merrill Flood y Melvin Dresher en 1950 mientras trabajaban en RAND. Albert W. Tucker luego formalizó el juego al estructurar las recompensas en términos de penas de prisión y lo denominó "dilema del prisionero". William Poundstone describió el juego en su libro de 1993 Prisoner's Dilemma:
Dos miembros de una banda criminal son arrestados y encarcelados. Cada preso está en régimen de aislamiento sin medios de hablar ni intercambiar mensajes con el otro. La policía admite que no tienen suficientes pruebas para condenar al par por el cargo principal. Planean condenar a dos años de prisión por un cargo menor. Simultáneamente, la policía ofrece a cada prisionero un trato Faustiano.
Los posibles resultados son:
- R: Si A y B cada uno traiciona al otro, cada uno sirve 5 años de prisión.
- B: Si A traiciona B pero B permanece en silencio, A será liberado mientras B cumple 10 años de prisión.
- C: Si A permanece en silencio pero B traiciona A, A servirá 10 años de prisión y B será liberado.
- D: Si ambos A y B permanecen en silencio, cada uno será el cargo menor de 2 años de prisión.
Como una proyección del comportamiento racional en términos de lealtad al socio en el crimen, el Dilema del Prisionero sugiere que los delincuentes a los que se les ofrece una recompensa mayor traicionarán a su socio.
La lealtad a la pareja es, en este juego, irracional. Esta suposición particular de racionalidad implica que el único resultado posible para dos prisioneros puramente racionales es la traición, aunque la cooperación mutua produciría una recompensa neta mayor. Se han propuesto ideas alternativas que gobiernan el comportamiento; véase, por ejemplo, Elinor Ostrom.
Traicionar es la estrategia dominante para ambos jugadores, lo que significa que es la mejor respuesta del jugador en todas las circunstancias, lo que se alinea con el principio de certeza. El dilema del prisionero también ilustra que las decisiones tomadas bajo la racionalidad colectiva pueden no ser necesariamente las mismas que las tomadas bajo la racionalidad individual. Este conflicto también es evidente en una situación llamada "Tragedia de los comunes".
En realidad, el sesgo sistémico hacia el comportamiento cooperativo ocurre a pesar de las predicciones de modelos simples de comportamiento "racional" acción interesada. Este sesgo hacia la cooperación ha sido evidente desde que este juego se llevó a cabo por primera vez en RAND: los secretarios involucrados a menudo confiaban entre sí y trabajaban juntos para lograr el mejor resultado común.
El dilema del prisionero se convirtió en el foco de una extensa investigación experimental. Esta investigación ha tomado una de tres formas: juego individual, juego iterado y juego iterado contra un jugador programado. La investigación sobre el dilema del prisionero ha servido para justificar el imperativo categórico planteado por Immanuel Kant, que afirma que se espera que un agente racional "actúe de la forma en que desea que actúen los demás". Esta teoría es vital para una situación que involucra a diferentes jugadores, cada uno de los cuales actúa en su mejor interés y debe cuidar a los demás. acciones en consideración para formar su propia elección.
Un extenso "iterado" También existe una versión del juego. En esta versión, el clásico juego se juega repetidamente entre los mismos presos, quienes continuamente tienen la oportunidad de penalizar al otro por decisiones anteriores. Si los jugadores conocen el número de veces que se jugará el juego, entonces, por inducción hacia atrás, dos jugadores clásicamente racionales se traicionarán repetidamente, por las mismas razones que la variante de un solo tiro. En un juego de duración infinita o desconocida no existe una estrategia óptima fija, y se han realizado torneos de dilema del prisionero para competir y probar algoritmos para tales casos.
La versión iterada del dilema del prisionero es de particular interés para los investigadores. Debido a su naturaleza iterativa, investigadores anteriores observaron que la frecuencia con la que los jugadores cooperan podría cambiar, según los resultados de cada iteración. Específicamente, un jugador puede estar menos dispuesto a cooperar si su contraparte no cooperó muchas veces, lo que lo decepciona. Por el contrario, a medida que pasa el tiempo, la cooperación puede aumentar debido a la configuración de un "acuerdo tácito" entre jugadores. Otro aspecto relacionado con la versión iterada del experimento es que este acuerdo tácito entre los jugadores siempre se ha establecido con éxito, incluso cuando el número de iteraciones se hace público para ambas partes.
El juego del dilema del prisionero puede modelar muchas situaciones del mundo real que involucran un comportamiento cooperativo. En uso casual, la etiqueta "dilema del prisionero" puede aplicarse a cualquier situación en la que dos entidades puedan obtener importantes beneficios de la cooperación o sufrir por no hacerlo, pero encuentran difícil o costoso, aunque no necesariamente imposible, coordinar sus actividades.
Estrategia para el dilema del prisionero
Dos presos están separados en habitaciones individuales y no pueden comunicarse entre sí. El juego normal se muestra a continuación:
Prisionero B Prisionero A | Prisionero B calla ()cooperaciones) | Prisionero B traiciona ()defectos) |
|---|---|---|
| Prisoner Una estancia silenciosa ()cooperaciones) | Cada uno sirve 2 años | Prisionero A: 10 años Prisionero B: va libre |
| Prisoner Una traición ()defectos) | Prisionero A: va libre Prisionero B: 10 años | Cada uno sirve 5 años |
Se supone que ambos prisioneros entienden la naturaleza del juego, no tienen lealtad entre ellos y no tendrán oportunidad de retribución o recompensa fuera del juego. Independientemente de lo que decida el otro, cada prisionero obtiene una recompensa mayor por traicionar al otro ("desertar"). El razonamiento consiste en analizar a ambos jugadores' mejores respuestas: B cooperará o desertará. Si B coopera, A debería desertar, porque salir libre es mejor que cumplir 2 años. Si B deserta, A también debería desertar, porque cumplir 5 años es mejor que cumplir 10. Entonces, de cualquier manera, A debería desertar ya que desertar es la mejor respuesta de A, independientemente de la estrategia de B. El razonamiento paralelo mostrará que B debería desertar.
La deserción siempre resulta en una mejor recompensa que la cooperación, por lo que es una estrategia estrictamente dominante tanto para A como para B. La deserción mutua es el único equilibrio fuerte de Nash en el juego (es decir, el único resultado a partir del cual cada jugador podría hacerlo peor). cambiando unilateralmente de estrategia). El dilema, entonces, es que la cooperación mutua produce un mejor resultado que la deserción mutua, pero no es el resultado racional porque la elección de cooperar, desde una perspectiva de interés propio, es irracional. Por lo tanto, el dilema del prisionero es un juego en el que el equilibrio de Nash no es eficiente en el sentido de Pareto.
Forma generalizada
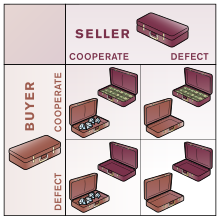
La estructura del dilema del prisionero tradicional se puede generalizar a partir de su escenario original del prisionero. Suponga que los dos jugadores están representados por los colores rojo y azul y que cada jugador elige "cooperar" (permanecer en silencio) o "defecto" (traicionar).
Si ambos jugadores cooperan, ambos reciben la recompensa R por cooperar. Si ambos jugadores desertan, ambos reciben el pago de castigo P. Si Azul deserta mientras que Rojo coopera, entonces Azul recibe el pago de la tentación T, mientras que Rojo recibe el "tonto's" pago, S. De manera similar, si Azul coopera mientras que Rojo deserta, entonces Azul recibe el pago del tonto S, mientras que Rojo recibe el pago de la tentación T.
Esto se puede expresar en forma normal:
Rojo Azul | Cooperate | Defecto |
|---|---|---|
| Cooperate | R R | T S |
| Defecto | S T | P P |
y para ser un juego de dilema del prisionero en el sentido fuerte, la siguiente condición debe cumplirse para los pagos:
- R>P>S}" xmlns="http://www.w3.org/1998/Math/MathML">T■R■P■S{displaystyle T títulor títulos
R>P>S}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fe6fac90a83474d2b977ae4ff2075c146534cb60" style="vertical-align: -0.338ex; width:15.94ex; height:2.176ex;"/>
La relación de pago P}" xmlns="http://www.w3.org/1998/Math/MathML">R■P{displaystyle R]P}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/37afbcb755b88dab03bced457fbdbcd90d55a904" style="vertical-align: -0.338ex; width:6.608ex; height:2.176ex;"/> implica que la cooperación mutua es superior a la deserción mutua, mientras que las relaciones de pago R}" xmlns="http://www.w3.org/1998/Math/MathML">T■R{displaystyle T títuloR}
R}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0d1fa60c9da906b73422a9f79364c30dda045601" style="vertical-align: -0.338ex; width:6.499ex; height:2.176ex;"/> y S}" xmlns="http://www.w3.org/1998/Math/MathML">P■S{displaystyle P títuloS}
S}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b7edfe25ef9f2cf28786fe0526e7104453dbda43" style="vertical-align: -0.338ex; width:6.343ex; height:2.176ex;"/> implica que la deserción es la estrategia dominante para ambos agentes.
Caso especial: juego de donación
El "juego de donaciones" es una forma de dilema del prisionero en el que la cooperación corresponde a ofrecer al otro jugador un beneficio b a un costo personal c con b > c. La deserción significa no ofrecer nada. La matriz de pagos es por lo tanto
Rojo Azul | Cooperate | Defecto |
|---|---|---|
| Cooperate | b−c b−c | b −c |
| Defecto | −c b | 0 0 |
Note que T+S}" xmlns="http://www.w3.org/1998/Math/MathML">2R■T+S{displaystyle 2R]T+S}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b75e44a0fe5e91b7367b6fe318f0aa3e84066e10" style="vertical-align: -0.505ex; width:12.001ex; height:2.343ex;"/> (i.e. b-c}" xmlns="http://www.w3.org/1998/Math/MathML">2()b− − c)■b− − c{displaystyle 2(b-c)
b-c}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/86f7c78701c47d21d1eaefe880c4e61e88d7322d" style="vertical-align: -0.838ex; width:15.76ex; height:2.843ex;"/>), que califica el juego de donación para ser un juego iterado (ver la siguiente sección).
El juego de la donación puede aplicarse a los mercados. Supongamos que X produce naranjas e Y produce manzanas. La utilidad marginal de una manzana para el productor de naranjas X es b, que es mayor que la utilidad marginal (c) de una naranja, ya que X tiene un excedente de naranjas y sin manzanas. De manera similar, para el productor de manzanas Y, la utilidad marginal de una naranja es b mientras que la utilidad marginal de una manzana es c. Si X e Y contratan intercambiar una manzana y una naranja, y cada uno cumple con su parte del trato, entonces cada uno recibe un pago de b-c. Si uno "defecto" y no cumple lo prometido, el desertor recibirá un pago de b, mientras que el cooperador perderá c. Si ambos desertan, entonces ninguno gana o pierde nada.
El dilema del prisionero iterado
Si dos jugadores juegan al dilema del prisionero más de una vez seguidas y recuerdan las acciones anteriores de su oponente y cambian su estrategia en consecuencia, el juego se denomina dilema del prisionero iterado.
Además de la forma general anterior, la versión iterativa también requiere que T+S}" xmlns="http://www.w3.org/1998/Math/MathML">2R■T+S{displaystyle 2R]T+S}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b75e44a0fe5e91b7367b6fe318f0aa3e84066e10" style="vertical-align: -0.505ex; width:12.001ex; height:2.343ex;"/>, para evitar la alternancia de la cooperación y la deserción dando una mayor recompensa que la cooperación mutua.
El juego del dilema del prisionero iterado es fundamental para algunas teorías de la cooperación y la confianza humanas. Suponiendo que el juego modele efectivamente las transacciones entre dos personas que requieren confianza, el comportamiento cooperativo en las poblaciones se puede modelar mediante una versión iterada del juego para varios jugadores. En 1975, Grofman y Pool estimaron la cantidad de artículos académicos dedicados a él en más de 2000. El dilema del prisionero iterado también se conoce como el "juego de paz y guerra".
Si el juego se juega N veces y ambos jugadores lo saben, entonces la estrategia dominante es desertar en todas las rondas. El único equilibrio de Nash posible es desertar siempre. La prueba es inductiva: uno también podría desertar en el último turno, ya que el oponente no tendrá la oportunidad de tomar represalias más tarde. Por lo tanto, ambos desertarán en el último turno. Por lo tanto, el jugador también podría desertar en el penúltimo turno, ya que el oponente desertará en el último sin importar lo que se haga, y así sucesivamente. Lo mismo se aplica si se desconoce la duración del juego pero tiene un límite superior conocido.
A diferencia del dilema del prisionero estándar, en el dilema del prisionero iterado, la estrategia de deserción es contraria a la intuición y no logra predecir el comportamiento de los jugadores humanos, a pesar de que la deserción es la única respuesta correcta en el dilema económico estándar. teoría. La estrategia superracional en el dilema del prisionero iterado con N fijo es cooperar contra un oponente superracional, y en el límite de grandes N, los resultados experimentales sobre las estrategias se alinean con la versión superracional en lugar de la racional basada en la teoría de juegos.
Para que surja la cooperación entre los jugadores racionales teóricos del juego, los jugadores deben desconocer el número de rondas N. En este caso "siempre defecto" puede que ya no sea una estrategia estrictamente dominante sino solo un equilibrio de Nash. Como lo demostró Robert Aumann en un artículo de 1959, los jugadores racionales que interactúan repetidamente durante juegos indefinidamente largos pueden mantener el resultado cooperativo.
Según un estudio experimental de 2019 en American Economic Review que probó qué estrategias usaron los sujetos de la vida real en los prisioneros iterativos & # 39; Situaciones de dilema con un seguimiento perfecto, la mayoría de las estrategias elegidas fueron siempre para desertar, ojo por ojo y gatillo sombrío. La estrategia que eligieron los sujetos dependía de los parámetros del juego.
Estrategia para el dilema del prisionero iterado
El interés por el dilema iterado del prisionero (DPI) fue despertado por Robert Axelrod en su libro La evolución de la cooperación (1984), en el que informa sobre un torneo que organizó de el dilema del prisionero del paso N (con N fijo) en el que los participantes tienen que elegir su estrategia mutua una y otra vez, y recordar sus encuentros anteriores. Axelrod invitó a colegas académicos de todo el mundo a diseñar estrategias informáticas para competir en un torneo IPD. Los programas que se ingresaron variaban ampliamente en complejidad algorítmica, hostilidad inicial, capacidad de perdón, etc.
Axelrod descubrió que cuando estos encuentros se repetían durante un largo período de tiempo con muchos jugadores, cada uno con diferentes estrategias, las estrategias codiciosas tendían a funcionar muy mal a largo plazo, mientras que las estrategias más altruistas funcionaban mejor, según lo juzgado puramente por la autoevaluación. interés. Usó esto para mostrar un posible mecanismo para la evolución del comportamiento altruista a partir de mecanismos que inicialmente son puramente egoístas, por selección natural.
La estrategia determinista ganadora fue ojo por ojo, que Anatol Rapoport desarrolló e ingresó al torneo. Fue el más simple de todos los programas presentados, con solo cuatro líneas de BASIC, y ganó el concurso. La estrategia es simplemente cooperar en la primera iteración del juego; después de eso, el jugador hace lo que hizo su oponente en el movimiento anterior. Dependiendo de la situación, una estrategia un poco mejor puede ser "ojo por ojo con perdón". Cuando el oponente deserta, en el siguiente movimiento, el jugador a veces coopera de todos modos, con una pequeña probabilidad (alrededor de 1 a 5%). Esto permite la recuperación ocasional de quedar atrapado en un ciclo de deserciones. La probabilidad exacta depende de la alineación de los oponentes.
Después de analizar las estrategias de mayor puntuación, Axelrod estableció varias condiciones necesarias para que una estrategia tenga éxito:
- Bonito
- La condición más importante es que la estrategia debe ser "nice". Es decir, no se defectará antes de que su oponente lo haga (a veces se denomina un algoritmo "optimista"). Casi todas las estrategias de alto nivel eran buenas. Una estrategia puramente egoísta no "será" en su oponente por razones puramente interesadas primero.
- Retaliating
- Sin embargo, Axelrod contended, la estrategia exitosa no debe ser un optimista ciego; a veces debe tomar represalias. Un ejemplo de una estrategia de no represalia es Siempre Cooperar. Esta es una muy mala elección, ya que las estrategias de "nastía" explotarán despiadadamente tales jugadores.
- Perdona.
- Las estrategias exitosas también deben ser indulgentes. Aunque los jugadores tomen represalias, volverán a caer para cooperar si el oponente no sigue desertando. Esto detiene largos recorridos de venganza y contrarrevención, maximizando puntos.
- Non-envious
- La última calidad es ser no envidiable, lo que significa no esforzarse por marcar más que el oponente.
La estrategia óptima (maximización de puntos) para el juego de PD de una sola vez es simplemente la deserción; como se explicó anteriormente, esto es cierto cualquiera que sea la composición de los oponentes. Sin embargo, en el juego de PD iterado, la estrategia óptima depende de las estrategias de los posibles oponentes y de cómo reaccionarán ante las deserciones y cooperaciones. Por ejemplo, considere una población donde todos desertan cada vez, excepto un solo individuo que sigue la estrategia de ojo por ojo. Ese individuo está en ligera desventaja debido a la pérdida en el primer turno. En tal población, la estrategia óptima para ese individuo es desertar cada vez. En una población con un cierto porcentaje de siempre desertores y el resto de jugadores de ojo por ojo, la estrategia óptima para un individuo depende del porcentaje y de la duración del juego.
En la estrategia llamada Pavlov, ganar-permanecer, perder-cambiar, ante la falta de cooperación, el jugador cambia de estrategia en el siguiente turno. En ciertas circunstancias, Pavlov supera a todas las demás estrategias al dar un trato preferencial a los jugadores que usan una estrategia similar.
La obtención de la estrategia óptima generalmente se realiza de dos maneras:
- Equilibrio Bayesian Nash: Si se puede determinar la distribución estadística de estrategias opuestas (por ejemplo, 50% de propinas, 50% siempre coopera) una contra-estrategia óptima puede derivarse analíticamente.
- Se han realizado simulaciones de poblaciones de Monte Carlo, donde los individuos con puntajes bajos mueren, y los con puntajes altos se reproducen (un algoritmo genético para encontrar una estrategia óptima). La mezcla de algoritmos en la población final generalmente depende de la mezcla en la población inicial. La introducción de mutación (variación rara durante la reproducción) disminuye la dependencia de la población inicial; experimentos empíricos con tales sistemas tienden a producir tit para los jugadores de tat (véase por ejemplo Chess 1988), pero no existe ninguna prueba analítica que esto siempre ocurra.
Aunque ojo por ojo se considera la estrategia básica más sólida, un equipo de la Universidad de Southampton en Inglaterra presentó una nueva estrategia en la competencia iterada del dilema del prisionero del vigésimo aniversario, que demostró ser más exitosa que ojo por ojo. para tatuaje Esta estrategia se basó en la colusión entre programas para lograr el mayor número de puntos para un solo programa. La universidad presentó 60 programas a la competencia, que fueron diseñados para reconocerse entre sí a través de una serie de cinco a diez movimientos al comienzo. Una vez hecho este reconocimiento, un programa siempre cooperaría y el otro siempre desertaría, asegurando el máximo número de puntos para el desertor. Si el programa se diera cuenta de que estaba jugando con un jugador que no era del Southampton, desertaría continuamente en un intento de minimizar el puntaje del programa competidor. Como resultado, el 2004 Prisoners' Los resultados del Torneo Dilemma muestran las estrategias de la Universidad de Southampton en los primeros tres lugares, a pesar de tener menos victorias y muchas más derrotas que la estrategia GRIM. (En un torneo de PD, el objetivo del juego no es 'ganar' partidos, eso se puede lograr fácilmente mediante la deserción frecuente). Esta estrategia terminó ocupando las tres primeras posiciones de la competencia, así como una serie de posiciones hacia la parte inferior.
La estrategia de Southampton aprovecha el hecho de que se permitían múltiples entradas en esta competición en particular y que el rendimiento de un equipo se medía por el del jugador con la puntuación más alta (lo que significa que el uso de jugadores abnegados era una forma de minmaxing). En una competencia donde uno tiene el control de un solo jugador, ojo por ojo es ciertamente una mejor estrategia. Debido a esta nueva regla, esta competencia también tiene poca importancia teórica al analizar las estrategias de un solo agente en comparación con el torneo seminal de Axelrod. Sin embargo, proporcionó una base para analizar cómo lograr estrategias cooperativas en marcos multiagente, especialmente en presencia de ruido. De hecho, mucho antes de que se jugara este torneo de nuevas reglas, Dawkins, en su libro The Selfish Gene, señaló la posibilidad de que tales estrategias ganaran si se permitían múltiples entradas, pero señaló que lo más probable es que Axelrod no los hubiera permitido si hubieran sido sometidos. También se basa en eludir las reglas sobre el dilema del prisionero en el sentido de que no se permite la comunicación entre los dos jugadores, lo que posiblemente hicieron los programas de Southampton con su 'baile de diez movimientos' preprogramado. reconocerse unos a otros; esto solo refuerza cuán valiosa puede ser la comunicación para cambiar el equilibrio del juego.
Incluso sin una colusión implícita entre las estrategias de software (explotadas por el equipo de Southampton), ojo por ojo no siempre es el ganador absoluto de un torneo dado; sería más preciso decir que sus resultados a largo plazo en una serie de torneos superan a sus rivales. (En cualquier caso, una estrategia determinada puede ajustarse un poco mejor a la competencia que ojo por ojo, pero ojo por ojo es más sólido). Lo mismo se aplica a la variante de ojo por ojo con perdón y otras estrategias óptimas: en un día determinado, es posible que no "ganen" contra una combinación específica de contraestrategias. Una forma alternativa de expresarlo es utilizando la simulación ESS darwiniana. En tal simulación, ojo por ojo casi siempre llegará a dominar, aunque las estrategias desagradables entrarán y saldrán de la población porque una población de ojo por ojo es penetrable por estrategias agradables que no toman represalias, que a su vez son presa fácil para los desagradables. estrategias. Richard Dawkins demostró que aquí, ninguna mezcla estática de estrategias forma un equilibrio estable y el sistema siempre oscilará entre límites.
Estocástico iteró el dilema de la prisionera
(feminine)En un juego stocástico iterated prisoner's dilemma juego, las estrategias se especifican en términos de "probabilidades de cooperación". En un encuentro entre jugador X y jugador Y, X's estrategia se especifica por un conjunto de probabilidades P de cooperación con Y. P es una función de los resultados de sus encuentros anteriores o algún subconjunto de ellos. Si P es una función de sólo su más reciente n encuentros, se llama "memory-n" estrategia. Una estrategia de memoria-1 se especifica entonces por cuatro probabilidades de cooperación: P={}Pcc,Pcd,Pdc,Pdd}{displaystyle P= {P_{cc},P_{cd},P_{dc},P_{dd}}, donde Pab{displaystyle P_{ab} es la probabilidad de que X cooperará en el presente encuentro dado que el encuentro anterior se caracterizó por (ab). Por ejemplo, si el encuentro anterior fue uno en el que X cooperado y cooperado Y desertado, entonces Pcd{displaystyle P_{cd} es la probabilidad de que X cooperará en el presente encuentro. Si cada una de las probabilidades son 1 o 0, la estrategia se llama determinista. Un ejemplo de estrategia determinista es la estrategia de punta por punta escrita como P={1,0,1,0}, en la que X responde como Y lo hizo en el encuentro anterior. Otra es la estrategia de ganar – quedarse, perder–switch escrita como P= {1,0,0,1}, en el que X responde como en el encuentro anterior, si era un "vino" (es decir, cc o dc) pero cambia la estrategia si era una pérdida (es decir, cd o dd). Se ha demostrado que para cualquier estrategia de memoria-n hay una estrategia correspondiente de memoria-1 que da los mismos resultados estadísticos, de modo que sólo las estrategias de memoria-1 deben ser consideradas.
Si definimos P como vector de estrategia de 4 elementos anterior X y Q={}Qcc,Qcd,Qdc,Qdd}{displaystyle Q={Q_{cc},Q_{cd},Q_{dc},Q_{dd}} como vector de estrategia de 4 elementos Y, una matriz de transición M puede definirse para X cuyo ij la probabilidad de que el resultado de un encuentro particular entre X y Y será j dado que el encuentro anterior fue i, donde i y j son uno de los cuatro índices de resultados: cc, cd, dc, o dd. Por ejemplo, de X's punto de vista, la probabilidad de que el resultado del presente encuentro sea cd dado que el encuentro anterior fue cd es igual a Mcd,cd=Pcd()1− − Qdc){displaystyle M_{cd,cd}=P_{cd}(1-Q_{dc}}. (Los índices para Q son de Y's punto de vista: a cd de los resultados X es un dc de los resultados Y.) Bajo estas definiciones, el dilema del prisionero iterado califica como un proceso estocástico y M es una matriz estocástica, permitiendo que se aplique toda la teoría de los procesos estocásticos.
Un resultado de la teoría estocástica es que existe un vector estacionario v para la matriz M tales que v⋅ ⋅ M=v{displaystyle vcdot M=v}. Sin pérdida de generalidad, puede especificarse que v se normaliza para que la suma de sus cuatro componentes sea unidad. El ij entrada Mn{displaystyle M^{n} dará la probabilidad de que el resultado de un encuentro entre X y Y será j dado que el encuentro n pasos anteriores i. En el límite como n enfoques infinito, M convergerá a una matriz con valores fijos, dando las probabilidades a largo plazo de un encuentro produciendo j que será independiente de i. En otras palabras, las filas de MJUEGO JUEGO {displaystyle M^{infty } será idéntico, dando el resultado del equilibrio a largo plazo las probabilidades del dilema del prisionero iterado sin la necesidad de evaluar explícitamente un gran número de interacciones. Se puede ver que v es un vector estacionario para Mn{displaystyle M^{n} en particular MJUEGO JUEGO {displaystyle M^{infty }, así que cada fila de MJUEGO JUEGO {displaystyle M^{infty } será igual a v. Así el vector estacionario especifica las probabilidades de equilibrio de resultados X. Definición Sx={}R,S,T,P}{displaystyle S_{x}={R,S,T,P} y SSí.={}R,T,S,P}{displaystyle S_{y}={R,T,S,P} como vectores de pago a corto plazo para los resultados {cc,cd,dc,dd} X's point of view), the equilibrium payoffs for X y Y ahora se puede especificar como sx=v⋅ ⋅ Sx{displaystyle S_{x}=vcdot S_{x} y sSí.=v⋅ ⋅ SSí.{displaystyle S_{y}=vcdot S_{y}, permitiendo las dos estrategias P y Q para ser comparado por sus pagos a largo plazo.
Estrategias de determinante cero

En 2012, William H. Press y Freeman Dyson publicaron una nueva clase de estrategias para el dilema del prisionero estócástico llamado estrategias "cero-determinantes" (ZD). Los pagos a largo plazo para los encuentros entre X y Y puede ser expresado como el determinante de una matriz que es una función de las dos estrategias y los vectores de pago a corto plazo: sx=D()P,Q,Sx){displaystyle s_{x}=D(P,Q,S_{x}} y sSí.=D()P,Q,SSí.){displaystyle S_{y}=D(P,Q,S_{y}}, que no implican el vector estacionario v. Desde la función determinante sSí.=D()P,Q,f){displaystyle s_{y}=D(P,Q,f)} es lineal en f, sigue que α α sx+β β sSí.+γ γ =D()P,Q,α α Sx+β β SSí.+γ γ U){displaystyle alpha s_{x}+beta s_{y}+gamma =D(P,Q,alpha S_{x}+beta S_{y}+gamma U)} (donde) U= {1,1,1,1}). Cualquier estrategia para la cual D()P,Q,α α Sx+β β SSí.+γ γ U)=0{displaystyle D(P,Q,alpha S_{x}+beta S_{y}+gamma U)=0} es por definición una estrategia ZD, y los pagos a largo plazo obedecen la relación α α sx+β β sSí.+γ γ =0{displaystyle alpha s_{x}+beta S_{y}+gamma =0}.
Tit-for-tat es una estrategia ZD que es "fair" en el sentido de no ganar ventaja sobre el otro jugador. Sin embargo, el espacio ZD también contiene estrategias que, en el caso de dos jugadores, pueden permitir que un jugador establezca unilateralmente la puntuación del otro jugador o alternativamente, obligan a un jugador evolutivo a lograr un pago un porcentaje inferior al suyo. El jugador extorsionado podría defectuarse, pero por lo tanto se haría daño por conseguir un pago más bajo. Así, las soluciones de extorsión convierten el dilema del prisionero iterado en una especie de juego ultimátum. Específicamente, X es capaz de elegir una estrategia para la cual D()P,Q,β β SSí.+γ γ U)=0{displaystyle D(P,Q,beta S_{y}+gamma U)=0}, establecimiento unilateral sSí.{displaystyle s_{y} a un valor específico dentro de una determinada gama de valores, independiente de Y's estrategia, ofreciendo una oportunidad para X para "extorsionar" jugador Y (y viceversa). (Resulta que si X Intenta establecer sx{displaystyle s_{x} a un valor particular, la gama de posibilidades es mucho menor, sólo consiste en una cooperación completa o una deserción completa.)
Una extensión del IPD es un IPD estocástico evolutivo, en el que se permite que cambie la abundancia relativa de estrategias particulares, con un aumento relativo de las estrategias más exitosas. Este proceso puede lograrse haciendo que los jugadores menos exitosos imiten las estrategias más exitosas, o eliminando del juego a los jugadores menos exitosos, mientras se multiplican los más exitosos. Se ha demostrado que las estrategias injustas de ZD no son evolutivamente estables. La intuición clave es que una estrategia evolutivamente estable no solo debe ser capaz de invadir a otra población (lo que pueden hacer las estrategias ZD extorsionadoras), sino que también debe funcionar bien contra otros jugadores del mismo tipo (que los jugadores ZD extorsionadores hacen mal porque se reducen entre sí& #39;s excedente).
La teoría y las simulaciones confirman que más allá de un tamaño de población crítico, la extorsión ZD pierde en la competencia evolutiva contra estrategias más cooperativas y, como resultado, el pago promedio en la población aumenta cuando la población es más grande. Además, hay algunos casos en los que los extorsionadores pueden incluso catalizar la cooperación al ayudar a salir de un enfrentamiento entre desertores uniformados y agentes que ganan, se quedan, pierden.
Si bien las estrategias extorsionadoras de ZD no son estables en grandes poblaciones, otra clase de ZD denominada "generosa" estrategias es tanto estable como robusta. De hecho, cuando la población no es demasiado pequeña, estas estrategias pueden suplantar a cualquier otra estrategia ZD e incluso funcionar bien frente a una amplia gama de estrategias genéricas para el dilema del prisionero iterado, que incluye ganar-quedarse, perder-cambiar. Esto fue probado específicamente para el juego de donación por Alexander Stewart y Joshua Plotkin en 2013. Las estrategias generosas cooperarán con otros jugadores cooperativos, y ante la deserción, el jugador generoso pierde más utilidad que su rival. Las estrategias generosas son la intersección de las estrategias ZD y las llamadas "buenas" estrategias, que fueron definidas por Akin (2013) como aquellas en las que el jugador responde a la cooperación mutua pasada con una cooperación futura y divide los pagos esperados en partes iguales si recibe al menos el pago esperado cooperativo. Entre las buenas estrategias, el subconjunto generoso (ZD) funciona bien cuando la población no es demasiado pequeña. Si la población es muy pequeña, las estrategias de deserción tienden a dominar.
Dilema del prisionero iterado continuo
La mayor parte del trabajo sobre el dilema del prisionero iterado se ha centrado en el caso discreto, en el que los jugadores cooperan o desertan, porque este modelo es relativamente simple de analizar. Sin embargo, algunos investigadores han analizado modelos del dilema del prisionero iterado continuo, en el que los jugadores pueden hacer una contribución variable al otro jugador. Le y Boyd encontraron que en tales situaciones, la cooperación es mucho más difícil de desarrollar que en el dilema del prisionero iterado discreto. La intuición básica para este resultado es sencilla: en un dilema continuo del prisionero, si una población comienza en un equilibrio no cooperativo, los jugadores que son solo marginalmente más cooperativos que los no cooperadores obtienen pocos beneficios al combinarse entre sí.. Por el contrario, en un dilema del prisionero discreto, los cooperadores de ojo por ojo obtienen un gran impulso de pago al relacionarse entre sí en un equilibrio no cooperativo, en relación con los no cooperadores. Dado que podría decirse que la naturaleza ofrece más oportunidades para la cooperación variable en lugar de una dicotomía estricta de cooperación o deserción, el dilema del prisionero continuo puede ayudar a explicar por qué los ejemplos de la vida real de cooperación tipo ojo por ojo son extremadamente raros en la naturaleza (ej., Hammerstein), aunque ojo por ojo parece sólido en los modelos teóricos.
Aparición de estrategias estables
Parece que los jugadores no pueden coordinar la cooperación mutua, por lo que a menudo quedan atrapados en la estrategia inferior pero estable de la deserción. De esta forma, las rondas iteradas facilitan la evolución de estrategias estables. Las rondas iteradas a menudo producen estrategias novedosas, que tienen implicaciones para la interacción social compleja. Una de esas estrategias es ganar-quedarse-perder-cambiar. Esta estrategia supera a una simple estrategia de ojo por ojo, es decir, si puede salirse con la suya haciendo trampa, repita ese comportamiento. Sin embargo, si te atrapan, cambia.
El único problema de esta estrategia de ojo por ojo es que son vulnerables a errores de señal. El problema surge cuando un individuo hace trampa en represalia pero el otro lo interpreta como trampa. Como resultado de esto, el segundo individuo ahora hace trampa y luego comienza un patrón de sube y baja de hacer trampa en una reacción en cadena.
Incluso sin juegos repetidos, un fuerte interés propio ilustrado puede dar como resultado un resultado estable y eficiente.
Ejemplos de la vida real
El escenario del prisionero puede parecer artificial, pero de hecho hay muchos ejemplos en la interacción humana, así como interacciones en la naturaleza que tienen la misma matriz de recompensas. El dilema del prisionero es, por tanto, de interés para las ciencias sociales como la economía, la política y la sociología, así como para las ciencias biológicas como la etología y la biología evolutiva. Muchos procesos naturales se han abstraído en modelos en los que los seres vivos se ven envueltos en interminables juegos del dilema del prisionero. Esta amplia aplicabilidad del PD le da al juego su importancia sustancial.
Estudios ambientales
En los estudios ambientales, la DP es evidente en crisis como el cambio climático global. Se argumenta que todos los países se beneficiarán de un clima estable, pero un solo país a menudo duda en frenar las emisiones de CO2. El beneficio inmediato para cualquier país de mantener el comportamiento actual se percibe como mayor que el supuesto beneficio final para ese país si todos los países & # 39; cambió el comportamiento, lo que explica el estancamiento en relación con el cambio climático en 2007.
Una diferencia importante entre la política del cambio climático y el dilema del prisionero es la incertidumbre; se desconoce el grado y el ritmo al que la contaminación puede cambiar el clima. El dilema que enfrentan los gobiernos es, por lo tanto, diferente del dilema del prisionero en que se desconocen los beneficios de la cooperación. Esta diferencia sugiere que los estados cooperarán mucho menos que en un dilema del prisionero iterado real, por lo que la probabilidad de evitar una posible catástrofe climática es mucho menor que la sugerida por un análisis de teoría de juegos de la situación utilizando un dilema del prisionero iterado real. dilema del prisionero.
Osang y Nandy (2003) brindan una explicación teórica con pruebas para una situación en la que todos ganan impulsada por la regulación en la línea de la hipótesis de Michael Porter, en la que la regulación gubernamental de las empresas competidoras es sustancial.
Animales
El comportamiento cooperativo de muchos animales puede entenderse como un ejemplo del dilema del prisionero. A menudo, los animales se involucran en asociaciones a largo plazo, que pueden modelarse más específicamente como el dilema del prisionero iterado. Por ejemplo, los guppies inspeccionan a los depredadores de manera cooperativa en grupos, y se cree que castigan a los inspectores que no cooperan.
Los murciélagos vampiros son animales sociales que se involucran en el intercambio recíproco de alimentos. Aplicar los pagos del dilema del prisionero puede ayudar a explicar este comportamiento:
- Cooperar/Cooperar: "Reward: Tengo sangre en mis noches de mala suerte, lo que me salva de morir de hambre. Tengo que darle sangre a mis noches de suerte, lo que no me cuesta demasiado".
- Defecto/Cooperación: "Temptación: Salvas mi vida en mi pobre noche. Pero entonces obtengo el beneficio añadido de no tener que pagar el ligero costo de alimentarte en mi buena noche."
- Cooperar/Defecto: "Sucker's Payoff: Pago el costo de salvar tu vida en mi buena noche. Pero en mi mala noche no me alimentas y corre un riesgo real de morir de hambre".
- Defecto/Defecto: "Mejoramiento: No tengo que pagar los ligeros costos de alimentarte en mis buenas noches. Pero corro un riesgo real de morir de hambre en mis malas noches."
Psicología
En la investigación sobre adicciones/economía del comportamiento, George Ainslie señala que la adicción se puede presentar como un problema de EP intertemporal entre el yo presente y el futuro del adicto. En este caso, desertar significa reincidir, y es fácil ver que no desertar tanto hoy como en el futuro es por mucho el mejor resultado. El caso en el que uno se abstiene hoy pero recae en el futuro es el peor resultado; en cierto sentido, la disciplina y el sacrificio propio que implica abstenerse hoy han sido "desperdiciados" porque la futura recaída significa que el adicto está justo donde empezó y tendrá que empezar de nuevo (lo cual es bastante desmoralizador y hace que empezar de nuevo sea más difícil). Recaer hoy y mañana es un poco "mejor" resultado, porque mientras el adicto sigue siendo adicto, no ha hecho el esfuerzo de tratar de dejarlo. El caso final, donde uno se involucra en el comportamiento adictivo hoy mientras se abstiene "mañana" será familiar para cualquiera que haya luchado contra una adicción. El problema aquí es que (como en otros PD) hay un beneficio obvio en desertar 'hoy', pero mañana uno se enfrentará al mismo PD, y el mismo beneficio obvio estará presente entonces, lo que en última instancia conducirá a un cadena interminable de deserciones.
John Gottman en su investigación descrita en "La ciencia de la confianza" define las buenas relaciones como aquellas en las que los socios saben que no deben ingresar a la celda (D,D) o al menos no quedar atrapados dinámicamente allí en un bucle. En la neurociencia cognitiva, la señalización cerebral rápida asociada con el procesamiento de diferentes rondas puede indicar opciones en la siguiente ronda. Los resultados de la cooperación mutua implican cambios en la actividad cerebral que predicen qué tan rápido una persona cooperará en especie en la próxima oportunidad; esta actividad puede estar vinculada a procesos homeostáticos y motivacionales básicos, posiblemente aumentando la probabilidad de atajar a la celda (C,C) del juego.
Economía
El dilema del prisionero ha sido llamado el E. coli de la psicología social, y se ha utilizado ampliamente para investigar diversos temas, como la competencia oligopólica y la acción colectiva para producir un bien colectivo.
La publicidad a veces se cita como un ejemplo real del dilema del prisionero. Cuando la publicidad de cigarrillos fue legal en los Estados Unidos, los fabricantes de cigarrillos de la competencia tuvieron que decidir cuánto dinero gastar en publicidad. La efectividad de la publicidad de la Firma A estuvo parcialmente determinada por la publicidad realizada por la Firma B. Asimismo, la ganancia derivada de la publicidad de la Firma B se ve afectada por la publicidad realizada por la Firma A. Si tanto la Firma A como la Firma B eligen publicidad durante un período determinado, entonces la publicidad de cada empresa anula la de la otra, los ingresos permanecen constantes y los gastos aumentan debido al costo de la publicidad. Ambas firmas se beneficiarían de una reducción en la publicidad. Sin embargo, si la empresa B decide no hacer publicidad, la empresa A podría beneficiarse enormemente de la publicidad. Sin embargo, la cantidad óptima de publicidad de una empresa depende de la cantidad de publicidad que realice la otra. Como la mejor estrategia depende de lo que elija la otra empresa, no existe una estrategia dominante, lo que lo hace ligeramente diferente del dilema del prisionero. Sin embargo, el resultado es similar en el sentido de que ambas empresas estarían mejor si anunciaran menos que en el equilibrio. A veces, los comportamientos cooperativos surgen en situaciones comerciales. Por ejemplo, los fabricantes de cigarrillos respaldaron la elaboración de leyes que prohíban la publicidad de cigarrillos, entendiendo que esto reduciría los costos y aumentaría las ganancias en toda la industria. Es probable que este análisis sea pertinente en muchas otras situaciones comerciales que involucran publicidad.
Sin acuerdos ejecutables, los miembros de un cártel también se ven envueltos en un dilema del prisionero (multijugador). 'Cooperando' generalmente significa mantener los precios en un nivel mínimo previamente acordado. 'Desertar' significa vender por debajo de este nivel mínimo, tomando instantáneamente negocios (y ganancias) de otros miembros del cartel. Las autoridades antimonopolio quieren que los miembros potenciales del cartel deserten mutuamente, asegurando los precios más bajos posibles para los consumidores.
Deporte
El dopaje en el deporte se ha citado como un ejemplo del dilema del prisionero.
Dos atletas que compiten tienen la opción de usar una droga ilegal y/o peligrosa para mejorar su rendimiento. Si ninguno de los atletas toma la droga, entonces ninguno obtiene una ventaja. Si solo uno lo hace, entonces ese atleta obtiene una ventaja significativa sobre su competidor, reducida por los peligros legales y/o médicos de haber tomado la droga. Sin embargo, si ambos atletas toman la droga, los beneficios se anulan y solo quedan los peligros, lo que los coloca a ambos en una posición peor que si ninguno hubiera usado el dopaje.
En una conversación con Ken Griffey Jr. después de la temporada de la MLB de 1998, Barry Bonds expresó su frustración con la opinión de otros jugadores. uso de esteroides. Bonds dijo: "Tuve una temporada increíble el año pasado y a nadie le importó una mierda". Nadie. Por mucho que me haya quejado de McGwire y Canseco y todo el toro con esteroides, estoy cansado de luchar contra eso. Cumplo 35 este año. Me quedan tres o cuatro buenas temporadas y quiero que me paguen. Voy a empezar a usar algunas cosas fuertes y espero que no dañen mi cuerpo. Entonces saldré del juego y terminaré con él." Bonds se encontró en el dilema del prisionero que es el dopaje en el béisbol, la sensación de que tiene que usar esteroides para que sus competidores no tengan una ventaja tan significativa sobre él, poniéndolo en igualdad de condiciones. aunque todos están peor que si nadie hubiera usado esteroides en absoluto.
Política internacional
En la teoría política internacional, el Dilema del Prisionero se usa a menudo para demostrar la coherencia del realismo estratégico, que sostiene que en las relaciones internacionales, todos los estados (independientemente de sus políticas internas o ideología profesada), actuarán en sus interés propio racional dada la anarquía internacional. Un ejemplo clásico es una carrera armamentista como la Guerra Fría y conflictos similares. Durante la Guerra Fría, las alianzas opuestas de la OTAN y el Pacto de Varsovia tenían la opción de armar o desarmar. Desde el punto de vista de cada bando, desarmarse mientras su oponente continuaba armándose habría llevado a una inferioridad militar y una posible aniquilación. Por el contrario, armar mientras su oponente estaba desarmado habría llevado a la superioridad. Si ambos lados optaban por armarse, ninguno podía permitirse atacar al otro, pero ambos incurrían en el alto costo de desarrollar y mantener un arsenal nuclear. Si ambos lados optaran por desarmarse, se evitaría la guerra y no habría costos.
Aunque el 'mejor' el resultado general es que ambos lados se desarme, el curso racional para ambos lados es armarse, y esto es de hecho lo que sucedió. Ambos bandos invirtieron enormes recursos en investigación militar y armamento en una guerra de desgaste durante los siguientes treinta años. La misma lógica podría aplicarse en cualquier escenario similar, ya sea competencia económica o tecnológica entre estados soberanos.
Dilemas multijugador
Muchos dilemas de la vida real involucran a varios jugadores. Aunque metafórica, la tragedia de los bienes comunes de Hardin puede verse como un ejemplo de una generalización multijugador de la PD: cada aldeano toma una decisión para beneficio personal o moderación. La recompensa colectiva por la deserción unánime (o incluso frecuente) son pagos muy bajos (que representan la destrucción de los 'bienes comunes'). Un dilema de bienes comunes con el que la mayoría de la gente puede identificarse es lavar los platos en una casa compartida. Al no lavar los platos, un individuo puede ganar ahorrando su tiempo, pero si todos los residentes adoptan ese comportamiento, el costo colectivo es que nadie tenga platos limpios.
Los bienes comunes no siempre se explotan: William Poundstone, en un libro sobre el dilema del prisionero, describe una situación en Nueva Zelanda donde las cajas de periódicos se dejan abiertas. Es posible que la gente tome un papel sin pagar (desertar), pero muy pocos lo hacen, sintiendo que si ellos no pagan, los demás tampoco, destruyendo el sistema. La investigación posterior de Elinor Ostrom, ganadora del Premio Nobel de Ciencias Económicas en 2009, planteó la hipótesis de que la tragedia de los comunes está demasiado simplificada, con el resultado negativo influido por influencias externas. Sin presiones complicadas, los grupos se comunican y administran los bienes comunes entre ellos para su beneficio mutuo, haciendo cumplir las normas sociales para preservar el recurso y lograr el máximo bien para el grupo, un ejemplo de lograr el mejor resultado para el caso de DP.
Juegos relacionados
Cambio de bolsa cerrada
Douglas Hofstadter sugirió una vez que a las personas a menudo les resulta más fácil entender problemas como el de DP cuando se ilustran en forma de un juego simple o de compensación. Uno de varios ejemplos que usó fue "intercambio de bolsa cerrada":
Dos personas se reúnen e intercambian bolsas cerradas, con el entendimiento de que una de ellas contiene dinero, y la otra contiene una compra. Cualquier jugador puede optar por honrar el trato poniendo en su bolsa lo que él o ella accedió, o él o ella puede defectuarse entregando una bolsa vacía.
¿Amiga o enemiga?
(feminine)¿Amigo o enemigo? es un programa de juegos que se emitió de 2002 a 2003 en Game Show Network en los EE. UU. Es un ejemplo del juego del dilema del prisionero probado en personas reales, pero en un escenario artificial. En el programa de juegos, compiten tres parejas de personas. Cuando se elimina una pareja, juegan un juego similar al dilema del prisionero para determinar cómo se dividen las ganancias. Si ambos cooperan (Amigo), comparten las ganancias 50–50. Si uno coopera y el otro deserta (enemigo), el desertor obtiene todas las ganancias y el cooperador no obtiene nada. Si ambos desertan, ambos se van sin nada. Tenga en cuenta que la matriz de recompensas es ligeramente diferente de la estándar dada anteriormente, ya que las recompensas por los "ambos defectos" y el "cooperar mientras el oponente deserta" los casos son idénticos. Esto hace que "ambos defectos" caso un equilibrio débil, en comparación con un equilibrio estricto en el dilema del prisionero estándar. Si un concursante sabe que su oponente va a votar 'Enemigo', entonces su propia elección no afecta sus propias ganancias. En un sentido específico, Friend or Foe tiene un modelo de recompensas entre el dilema del prisionero y el juego del pollo.
La matriz de recompensas es
Pareja 2 Pareja 1 | "Amigo" (cooperar) | "Foe" (defecto) |
|---|---|---|
| "Amigo" (cooperar) | 1 1 | 2 0 |
| "Foe" (defecto) | 0 2 | 0 0 |
Esta matriz de pagos también se ha utilizado en los programas de televisión británicos Trust Me, Shafted, The Bank Job y Golden Balls , y en los concursos americanos Take It All, así como para la pareja ganadora en los programas Reality Show Bachelor Pad y Love Island. Los datos del juego de la serie Golden Balls han sido analizados por un equipo de economistas, que descubrió que la cooperación era "sorprendentemente alta" por cantidades de dinero que parecerían importantes en el mundo real pero que eran comparativamente bajas en el contexto del juego.
Ventisquero iterado
Investigadores de la Universidad de Lausana y la Universidad de Edimburgo han sugerido que el "Juego iterado de ventisqueros" pueden reflejar más fielmente situaciones sociales del mundo real. Aunque este modelo es en realidad un juego de gallinas, se describirá aquí. En este modelo, el riesgo de ser explotado por deserción es menor, y los individuos siempre se benefician al tomar la decisión cooperativa. El juego de ventisqueros imagina a dos conductores atrapados en lados opuestos de un ventisquero, cada uno de los cuales tiene la opción de palear la nieve para despejar el camino o permanecer en su automóvil. La recompensa más alta de un jugador proviene de dejar que el oponente quite toda la nieve por sí mismo, pero el oponente aún recibe una recompensa nominal por su trabajo.
Esto puede reflejar mejor los escenarios del mundo real, los investigadores dan el ejemplo de dos científicos que colaboran en un informe, quienes se beneficiarían si el otro trabajara más duro. "Pero cuando tu colaborador no hace ningún trabajo, probablemente sea mejor que tú hagas todo el trabajo tú mismo. Igual terminará con un proyecto completo."
|
|
Juegos de coordinación
En los juegos de coordinación, los jugadores deben coordinar sus estrategias para obtener un buen resultado. Un ejemplo son dos autos que se encuentran abruptamente en una ventisca; cada uno debe elegir si virar bruscamente a la izquierda oa la derecha. Si ambos se desvían a la izquierda o ambos a la derecha, los autos no chocan. La convención local de tráfico por la izquierda y por la derecha ayuda a coordinar sus acciones.
Los juegos de coordinación simétrica incluyen la caza del ciervo y Bach o Stravinsky.
Los dilemas de la prisionera asimétrica
(feminine)Un conjunto más general de juegos son los asimétricos. Como en el dilema del prisionero, el mejor resultado es la cooperación y hay motivos para la deserción. Sin embargo, a diferencia del dilema del prisionero simétrico, un jugador tiene más que perder y/o más que ganar que el otro. Algunos de estos juegos se han descrito como un dilema del prisionero en el que un prisionero tiene una coartada, de ahí el término "juego de coartada".
En los experimentos, los jugadores que obtienen pagos desiguales en juegos repetidos pueden buscar maximizar las ganancias, pero solo bajo la condición de que ambos jugadores reciban pagos iguales; esto puede conducir a una estrategia de equilibrio estable en la que el jugador en desventaja deserta cada X juegos, mientras que el otro siempre coopera. Tal comportamiento puede depender de las normas sociales del experimento en torno a la equidad.
Dilema de la tutora
(feminine)No solo los prisioneros enfrentan dilemas. Los guardianes también se enfrentan a situaciones en las que solo hay opciones poco atractivas entre las que elegir. Se pueden encontrar fácilmente ejemplos en casos en los que un agente debe suavizar las tensiones entre sus propios socios: uno puede pensar en dos colegas compitiendo para avanzar en su carrera y los problemas que esto le causa al director general de su empresa; dos funcionarios que compiten por el ascenso y la tensión que esto genera para el jefe de su gabinete; o en la crianza de los hijos cuando dos hermanos compiten por la atención y la ansiedad que esto les causa a sus padres. Si el comportamiento del guardián satisface a un lado, el otro lado se siente expuesto y alienado.
Desde la perspectiva de las relaciones internacionales, el Dr. Spyros Katsoulas presenta el concepto del dilema del guardián. El dilema del guardián se define como la condición en la que dos estados mantienen su enemistad entre sí a pesar de compartir un aliado común más fuerte. Por defecto, un dilema es una situación con opciones insatisfactorias. El dilema del guardián radica en el hecho de que el estado más fuerte no puede mantenerse al margen de una crisis entre sus aliados ni involucrarse activamente sin afectar el frágil equilibrio. Si el tutor se abstiene, la situación puede salirse de control; si el guardián se involucra, cualquier inclinación en contra de un lado puede verse como una victoria o una ventana de oportunidad para el otro. Ampliando el concepto de Glenn Snyder del dilema de seguridad de la alianza, los resultados de la interacción entre el guardián y los dos socios más pequeños se describen como abandono, atrapamiento y envalentonamiento.
Software
Se han creado varios paquetes de software para ejecutar simulaciones y torneos del dilema del prisionero, algunos de los cuales tienen código fuente disponible.
- El código fuente para el segundo torneo de Robert Axelrod (escrito por Axelrod y muchos colaboradores en Fortran) está disponible en línea
- Prison, a library written in Java, last updated in 1998
- Axelrod-Python, escrito en Python
- Evoplex, un rápido programa de modelado basado en agentes lanzado en 2018 por Marcos Cardinot
En la ficción
Hannu Rajaniemi situó la escena inicial de su trilogía The Quantum Thief en una "prisión de dilemas". El tema principal de la serie ha sido descrito como la "insuficiencia de un universo binario" y el último antagonista es un personaje llamado All-Desector. Rajaniemi es particularmente interesante como artista que trata este tema, ya que es un matemático formado en Cambridge y tiene un doctorado. en física matemática: la intercambiabilidad de la materia y la información es una característica importante de los libros, que tienen lugar en una "possingularidad" futuro. El primer libro de la serie se publicó en 2010, con las dos secuelas, The Fractal Prince y The Causal Angel, publicadas en 2012 y 2014, respectivamente.
Un juego inspirado en el dilema del prisionero (iterado) es un enfoque central del videojuego de 2012 Zero Escape: Virtue's Last Reward y una parte menor en su 2016 secuela Zero Escape: Zero Time Dilemma.
En The Mysterious Benedict Society and the Prisoner's Dilemma de Trenton Lee Stewart, los personajes principales comienzan jugando una versión del juego y escapando de la "prisión" en total. Más tarde se convierten en prisioneros reales y escapan una vez más.
En The Adventure Zone: Balance durante el subarco The Suffering Game, a los personajes jugadores se les presenta dos veces el dilema del prisionero durante su tiempo en dos liches. 39; dominio, una vez cooperando y una vez desertando.
En la octava novela del autor James S. A. Corey La ira de Tiamat, Winston Duarte explica el dilema del prisionero a su hija de 14 años, Teresa, para entrenar ella en el pensamiento estratégico.
Una versión extrema del dilema del prisionero se presenta en la película de 2008 The Dark Knight en la que el Joker manipula dos transbordadores, uno con prisioneros y otro con civiles, armando a ambos grupos. con los medios para detonar la bomba en los transbordadores de cada uno. En última instancia, las dos partes deciden no actuar.
Contenido relacionado
Algoritmo de Bellman-Ford
Paisaje fractal
Johann Friedrich Endersch