Desviación mediana

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

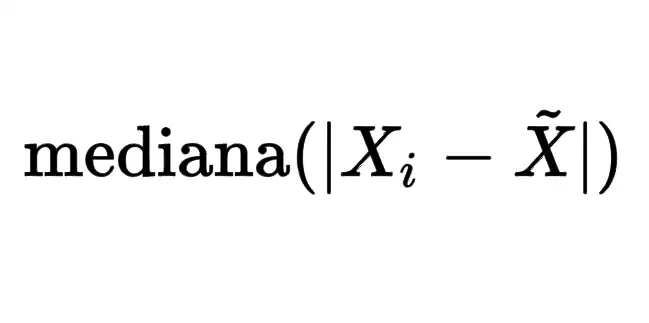
Fórmula de la desviación mediana, donde X_i es cada value y X̄ el valor promedio

La desviación mediana absoluta o simplemente desviación mediana, es una forma de medir la dispersión estadística de un conjunto de datos usando las diferencias absolutas entre cada unidad estadística y la mediana del conjunto de datos. En otras palabras, es la mediana de las desviaciones absolutas de la mediana del conjunto. No debe confundirse con la desviación media.

Para calcular la desviación mediana se debe:

Encontrar la diferencia absoluta entre cada punto de datos y la mediana.
Calcular la mediana de estas diferencias absolutas.

La desviación mediana se considera una medida robusta de la dispersión (variabilidad) de un conjunto de datos cuantitativos univariados, a diferencia de la varianza o de la desviación estándar, que se ven más afectadas por valores extremos y distribuciones no-normales. Un bajo valor de desviación mediana indica que los datos están cerca de la mediana y tienen baja variabilidad. Un alto valor de desviación mediana significa que los datos están lejos de la mediana y tienen alta variabilidad.

La desviación mediana no solo se aplica descriptivamente a muestras de datos, sino que también puede extenderse para inferir el parámetro correspondiente en una población completa. Esto se logra a través del cálculo de la desviación mediana en una muestra representativa, ofreciendo una visión de la variabilidad poblacional.

Es importante señalar que la desviación mediana no se calcula directamente sobre el conjunto de datos, sino sobre el conjunto resultante de las medianas del conjunto (residual), medidas solo en sus valores absolutos, de allí su nombre. Por lo que la desviación mediana no presenta datos sobre la población, sino exclusivamente cuantifica la variabilidad.

Este enfoque residual, centrado en la mediana para evaluar la variabilidad asegura que la desviación mediana sea menos susceptible a las fluctuaciones extremas en los datos, comparada con otras medidas de dispersión, y es ampliamente aceptada como una medida de variabilidad robusta y fiable.

HSD

Ejemplo

Considere los datos (1, 1, 2, 2, 4, 6, 9). Tiene un valor mediano de 2. Las desviaciones absolutas sobre 2 son (1, 1, 0, 0, 2, 4, 7) que a su vez tienen un valor mediano de 1 (porque las desviaciones absolutas ordenadas son (0, 0, 1, 1, 2, 4, 7)). Entonces, la desviación absoluta mediana para estos datos es 1.

Usos

La desviación absoluta mediana es una medida de dispersión estadística. Además, la MAD es una estadística robusta, siendo más resistente a los valores atípicos en un conjunto de datos que la desviación estándar. En la desviación estándar, las distancias desde la media se elevan al cuadrado, por lo que las desviaciones grandes se ponderan más y, por lo tanto, los valores atípicos pueden influir en gran medida. En el MAD, las desviaciones de un pequeño número de valores atípicos son irrelevantes.

Debido a que la MAD es un estimador de escala más sólido que la varianza muestral o la desviación estándar, funciona mejor con distribuciones sin media o varianza, como la distribución de Cauchy.

Relación con la desviación estándar

La MAD se puede usar de manera similar a como se usaría la desviación para el promedio. Para utilizar la MAD como un estimador consistente para la estimación de la desviación estándar $sigma$ , se toma ${displaystyle {sombrero {sigma}}=kcdot operatorname {MAD},}$

donde $k$ es un factor de escala constante, que depende de la distribución.

Para los datos normalmente distribuidos $k$ se toma como ${displaystyle k=1/left(Phi ^{-1}(3/4)right)approx 1.4826,}$

es decir, el recíproco de la función cuantil $phi ^{-1}$ (también conocida como la inversa de la función de distribución acumulativa) para la distribución normal estándar ${displaystyle Z=(X-mu)/sigma }$ . El argumento 3/4 es tal que ${displaystyle pm operatorname {MAD} }$ cubre el 50% (entre 1/4 y 3/4) de la función de distribución acumulativa normal estándar, es decir ${displaystyle {frac {1}{2}}=P(|X-mu |leq operatorname {MAD})=Pleft(left|{frac {X-mu }{sigma }}right|leq {frac {operatorname {MAD} }{sigma }}right)=Pleft(|Z|leq {frac {operatorname {MAD} }{sigma }} derecho).}$

Por lo tanto, debemos tener que ${displaystyle Phi left(operatorname {MAD} /sigma right)-Phi left(-operatorname {MAD} /sigma right)=1/2.}$

notando que ${displaystyle Phi left(-operatorname {MAD} /sigma right)=1-Phi left(operatorname {MAD} /sigma right),}$

tenemos eso ${displaystyle operatorname {MAD} /sigma =Phi ^{-1}(3/4)=0.67449}$ , de donde obtenemos el factor de escala ${displaystyle k=1/Phi^{-1}(3/4)=1,4826}$ .

Otra forma de establecer la relación es notar que MAD es igual a la media de la distribución normal: ${displaystyle operatorname {MAD} =sigma {sqrt {2}}operatorname {erf} ^{-1}(1/2)approx 0.67449sigma.}$

Esta forma se utiliza, por ejemplo, en el error probable.

Desviación absoluta de una mediana geométrica

De manera similar a cómo la mediana se generaliza a la mediana geométrica en datos multivariados, se puede construir una MAD geométrica que generalice la MAD. Dado un par de datos bidimensionales (X ₁, Y ₁), (X ₂, Y ₂),..., (X _n, Y _n) y una mediana geométrica adecuadamente calculada ${ estilo de visualización ({ tilde {X}}, { tilde {Y}})}$ , la desviación absoluta de la mediana geométrica viene dada por:

{displaystyle operatorname {MAD} ={Bigl (}operatorname {mediana} (|X_{i}-{tilde {X}}|)^{2}+operatorname {mediana} (|Y_{i }-{tilde {Y}}|)^{2}{Bigr)}^{1/2}}

Esto da el mismo resultado que el MAD univariante en 1 dimensión y se extiende fácilmente a dimensiones superiores. En el caso de valores complejos (X +i Y), la relación de MAD con la desviación estándar no cambia para los datos normalmente distribuidos.

Población estimada por desviación mediana

La MAD poblacional se define de manera análoga a la MAD muestral, pero se basa en la distribución completa y no en una muestra. Para una distribución simétrica con media cero, la población MAD es el percentil 75 de la distribución.

A diferencia de la varianza, que puede ser infinita o indefinida, la MAD poblacional es siempre un número finito. Por ejemplo, la distribución estándar de Cauchy tiene una varianza indefinida, pero su MAD es 1.

La primera mención conocida del concepto de MAD se produjo en 1816, en un artículo de Carl Friedrich Gauss sobre la determinación de la precisión de las observaciones numéricas.

Contenido relacionado

Más resultados...