Modelo estadístico

Compartir Imprimir Citar

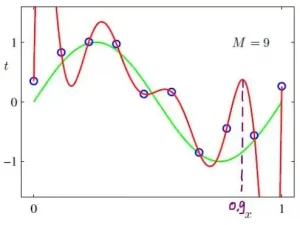
Un modelo estadístico o probabilístico es un modelo matemático que incorpora un conjunto de supuestos estadísticos relacionados con la generación de datos de muestra (y datos similares de una población más grande). Un modelo estadístico representa, a menudo en forma considerablemente idealizada, el proceso de generación de datos.

Un modelo estadístico generalmente se especifica como una relación matemática entre una o más variables aleatorias y otras variables no aleatorias. Como tal, un modelo estadístico es 'una representación formal de una teoría' (Herman Adèr citando a Kenneth Bollen).

Todas las pruebas de hipótesis estadísticas y todos los estimadores estadísticos se derivan a través de modelos estadísticos. De manera más general, los modelos estadísticos son parte de la base de la inferencia estadística.

Introducción

Toda red neuronal es un modelo estadístico

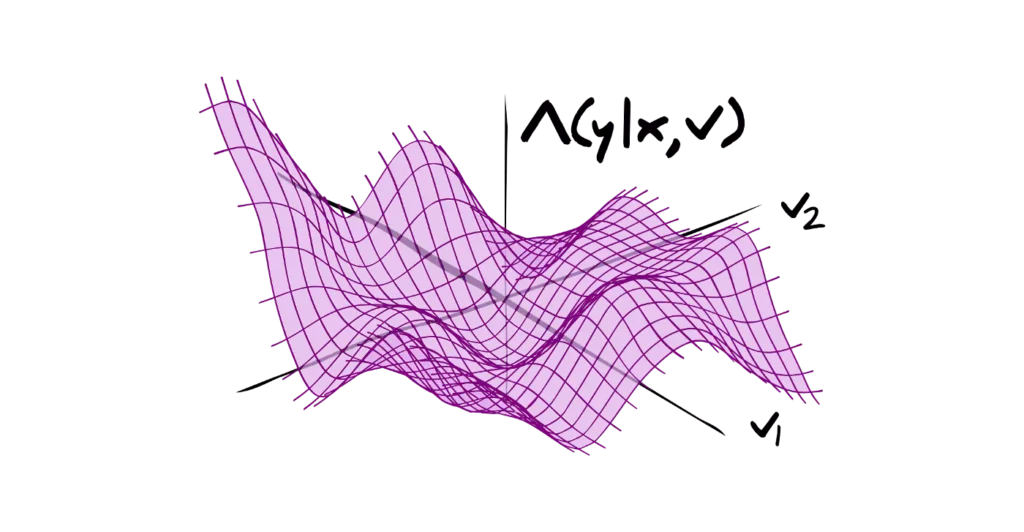
De manera informal, un modelo estadístico puede considerarse como una suposición estadística (o un conjunto de suposiciones estadísticas) con una determinada propiedad: que la suposición nos permite calcular la probabilidad de cualquier evento. Como ejemplo, considere un par de dados ordinarios de seis caras. Estudiaremos dos supuestos estadísticos diferentes sobre los dados.

La primera suposición estadística es la siguiente: para cada uno de los dados, la probabilidad de que salga cada cara (1, 2, 3, 4, 5 y 6) es 1/6. A partir de esa suposición, podemos calcular la probabilidad de que ambos dados salgan 5: 1/6×1/6 = 1/36. Más generalmente, podemos calcular la probabilidad de cualquier evento: por ejemplo (1 y 2) o (3 y 3) o (5 y 6).

La suposición estadística alternativa es la siguiente: para cada uno de los dados, la probabilidad de que salga la cara 5 es 1/8(porque los dados están ponderados). A partir de esa suposición, podemos calcular la probabilidad de que ambos dados salgan 5: 1/8×1/8 = 1/64. Sin embargo, no podemos calcular la probabilidad de ningún otro evento no trivial, ya que se desconocen las probabilidades de las otras caras.

El primer supuesto estadístico constituye un modelo estadístico: porque solo con el supuesto, podemos calcular la probabilidad de cualquier evento. El supuesto estadístico alternativo no constituye un modelo estadístico: porque con el supuesto solo, no podemos calcular la probabilidad de cada evento.

En el ejemplo anterior, con la primera suposición, calcular la probabilidad de un evento es fácil. Sin embargo, con algunos otros ejemplos, el cálculo puede ser difícil o incluso poco práctico (por ejemplo, podría requerir millones de años de cálculo). Para que una suposición constituya un modelo estadístico, tal dificultad es aceptable: hacer el cálculo no necesita ser practicable, solo teóricamente posible.

Definicion formal

En términos matemáticos, un modelo estadístico generalmente se considera como un par ( $S,{\mathcal {P}}$ ), donde $S$ es el conjunto de posibles observaciones, es decir, el espacio muestral, y ${\ matemáticas {P}}$ es un conjunto de distribuciones de probabilidad en $S$ .

La intuición detrás de esta definición es la siguiente. Se supone que existe una distribución de probabilidad "verdadera" inducida por el proceso que genera los datos observados. Nosotros elegimos ${\ matemáticas {P}}$ para representar un conjunto (de distribuciones) que contiene una distribución que se aproxima adecuadamente a la verdadera distribución.

Tenga en cuenta que no requerimos que ${\ matemáticas {P}}$ contiene la verdadera distribución, y en la práctica rara vez es el caso. De hecho, como afirman Burnham & Anderson, "Un modelo es una simplificación o aproximación de la realidad y, por lo tanto, no reflejará toda la realidad", de ahí el dicho "todos los modelos están equivocados".

El conjunto ${\ matemáticas {P}}$ casi siempre está parametrizado: ${\mathcal {P}}=\{P_{{\theta }}:\theta \in \Theta \}$ . El conjunto $\Theta$ define los parámetros del modelo. Por lo general, se requiere una parametrización para que valores de parámetros distintos den lugar a distribuciones distintas, es decir $P_{{\theta _{1}}}=P_{{\theta _{2}}}\flecha derecha \theta _{1}=\theta _{2}$ debe contener (en otras palabras, debe ser inyectiva). Se dice que una parametrización que cumple con el requisito es identificable .

Un ejemplo

Suponga que tenemos una población de niños, con las edades de los niños distribuidas uniformemente, en la población. La altura de un niño estará estocásticamente relacionada con la edad: por ejemplo, cuando sabemos que un niño tiene 7 años, esto influye en la probabilidad de que mida 1,5 metros. Podríamos formalizar esa relación en un modelo de regresión lineal, así: altura _i = b ₀ + b ₁ edad _i + ε _i , donde b ₀ es el intercepto, b ₁ es un parámetro por el que se multiplica la edad para obtener una predicción de altura, ε _i es el término de error, y iidentifica al niño. Esto implica que la altura se predice por la edad, con algún error.

Un modelo admisible debe ser consistente con todos los puntos de datos. Por lo tanto, una línea recta (altura _i = b ₀ + b ₁ edad _i ) no puede ser la ecuación para un modelo de los datos, a menos que se ajuste exactamente a todos los puntos de datos, es decir, todos los puntos de datos se encuentran perfectamente en la línea. El término de error, ε _i , debe incluirse en la ecuación para que el modelo sea consistente con todos los puntos de datos.

Para hacer una inferencia estadística, primero necesitaríamos asumir algunas distribuciones de probabilidad para el ε _i . Por ejemplo, podríamos suponer que las distribuciones ε _i son gaussianas iid, con media cero. En este caso, el modelo tendría 3 parámetros: b ₀ , b ₁ y la varianza de la distribución Gaussiana.

Podemos especificar formalmente el modelo en la forma ( $S,{\mathcal {P}}$ ) como sigue. El espacio muestral, $S$ , de nuestro modelo comprende el conjunto de todos los pares posibles (edad, altura). Cada valor posible de $\ theta$ = ( b ₀ , b ₁ , σ ) determina una distribución en $S$ ; denote que la distribución por $P_{{\theta}}$ . Si $\Theta$ es el conjunto de todos los valores posibles de $\ theta$ , entonces ${\mathcal {P}}=\{P_{{\theta }}:\theta \in \Theta \}$ . (La parametrización es identificable, y esto es fácil de verificar).

En este ejemplo, el modelo está determinado por (1) especificando $S$ y (2) hacer algunas suposiciones relevantes para ${\ matemáticas {P}}$ . Hay dos supuestos: que la altura se puede aproximar mediante una función lineal de la edad; que los errores en la aproximación se distribuyen como iid Gaussian. Los supuestos son suficientes para especificar ${\ matemáticas {P}}$ —como están obligados a hacerlo.

Observaciones generales

Un modelo estadístico es una clase especial de modelo matemático. Lo que distingue a un modelo estadístico de otros modelos matemáticos es que un modelo estadístico no es determinista. Así, en un modelo estadístico especificado mediante ecuaciones matemáticas, algunas de las variables no tienen valores específicos, sino que tienen distribuciones de probabilidad; es decir, algunas de las variables son estocásticas. En el ejemplo anterior con las alturas de los niños, ε es una variable estocástica; sin esa variable estocástica, el modelo sería determinista.

Los modelos estadísticos se utilizan a menudo incluso cuando el proceso de generación de datos que se modela es determinista. Por ejemplo, lanzar una moneda al aire es, en principio, un proceso determinista; sin embargo, comúnmente se modela como estocástico (a través de un proceso de Bernoulli).

La elección de un modelo estadístico apropiado para representar un proceso de generación de datos dado es a veces extremadamente difícil y puede requerir el conocimiento tanto del proceso como de los análisis estadísticos relevantes. De manera relacionada, el estadístico Sir David Cox ha dicho: "La forma en que se realiza [la] traducción del problema del tema al modelo estadístico es a menudo la parte más crítica de un análisis".

Hay tres propósitos para un modelo estadístico, según Konishi & Kitagawa.

predicciones
Extracción de información
Descripción de estructuras estocásticas

Esos tres propósitos son esencialmente los mismos que los tres propósitos señalados por Friendly & Meyer: predicción, estimación, descripción. Los tres propósitos se corresponden con los tres tipos de razonamiento lógico: razonamiento deductivo, razonamiento inductivo, razonamiento abductivo.

Dimensión de un modelo

Supongamos que tenemos un modelo estadístico ( $S,{\mathcal {P}}$ ) con ${\mathcal {P}}=\{P_{{\theta }}:\theta \in \Theta \}$ . Se dice que el modelo es paramétrico si $\Theta$ tiene una dimensión finita. En notación, escribimos que $\Theta \subseteq \mathbb {R} ^{k}$ donde k es un entero positivo ( $\matemáticas {R}$ denota los números reales; pueden utilizarse otros conjuntos, en principio). Aquí, k se llama la dimensión del modelo.

Como ejemplo, si suponemos que los datos surgen de una distribución gaussiana univariada, entonces estamos suponiendo que 0\right\ }}">.

En este ejemplo, la dimensión, k , es igual a 2.

Como otro ejemplo, suponga que los datos consisten en puntos ( x , y ) que asumimos que están distribuidos de acuerdo con una línea recta con residuos gaussianos iid (con media cero): esto conduce al mismo modelo estadístico que se usó en el ejemplo con alturas de los niños. La dimensión del modelo estadístico es 3: la intersección de la línea, la pendiente de la línea y la varianza de la distribución de los residuos. (Tenga en cuenta que en geometría, una línea recta tiene dimensión 1).

Aunque formalmente{\ estilo de visualización \ theta \ en \ Theta} $\theta \en \theta$ es un solo parámetro que tiene dimensión k , a veces se considera que comprende k parámetros separados. Por ejemplo, con la distribución gaussiana univariante,{\ estilo de visualización \ theta} $\ theta$ es formalmente un solo parámetro con dimensión 2, pero a veces se considera que comprende 2 parámetros separados: la media y la desviación estándar.

Un modelo estadístico es no paramétrico si el conjunto de parámetros{\ estilo de visualización \ theta} $\Theta$ es de infinitas dimensiones. Un modelo estadístico es semiparamétrico si tiene parámetros de dimensión finita e infinita. Formalmente, si k es la dimensión de{\ estilo de visualización \ theta} $\Theta$ y n es el número de muestras, tanto los modelos semiparamétricos como los no paramétricos tienen{\displaystyle k\rightarrow\infty} $k \rightarrow \infty$ como {\ estilo de visualización n \ flecha derecha \ infinito} $n\rightarrow\infty$ . Si{\ estilo de visualización k/n \ flecha derecha 0} ${\ estilo de visualización k/n \ flecha derecha 0}$ como {\ estilo de visualización n \ flecha derecha \ infinito} $n\rightarrow\infty$ , entonces el modelo es semiparamétrico; de lo contrario, el modelo es no paramétrico.

Los modelos paramétricos son, con diferencia, los modelos estadísticos más utilizados. Con respecto a los modelos semiparamétricos y no paramétricos, Sir David Cox ha dicho: "Por lo general, implican menos suposiciones de estructura y forma de distribución, pero generalmente contienen suposiciones sólidas sobre las independencias".

Modelos anidados

No debe confundirse con los modelos multinivel.

Dos modelos estadísticos están anidados si el primer modelo puede transformarse en el segundo modelo imponiendo restricciones a los parámetros del primer modelo. Como ejemplo, el conjunto de todas las distribuciones gaussianas tiene, anidado dentro de él, el conjunto de distribuciones gaussianas de media cero: restringimos la media en el conjunto de todas las distribuciones gaussianas para obtener las distribuciones de media cero. Como segundo ejemplo, el modelo cuadráticoy = segundo 0 + segundo ₁x + segundo ₂x + ε, ε ~ ? ( 0 _,σ )

tiene, anidado en su interior, el modelo linealy = segundo 0 + segundo ₁x + ε, ε ~ ?( 0 _,σ )

— restringimos el parámetro b ₂ a igual a 0.

En ambos ejemplos, el primer modelo tiene una dimensión más alta que el segundo modelo (para el primer ejemplo, el modelo de media cero tiene una dimensión 1). Tal es a menudo, pero no siempre, el caso. Como ejemplo diferente, el conjunto de distribuciones gaussianas de media positiva, que tiene dimensión 2, está anidado dentro del conjunto de todas las distribuciones gaussianas.

Comparando modelos

La comparación de modelos estadísticos es fundamental para gran parte de la inferencia estadística. De hecho, Konishi & Kitagawa (2008, p. 75) afirman esto: "La mayoría de los problemas en la inferencia estadística pueden considerarse problemas relacionados con el modelado estadístico. Por lo general, se formulan como comparaciones de varios modelos estadísticos".

Los criterios comunes para comparar modelos incluyen los siguientes: R , factor de Bayes, criterio de información de Akaike y la prueba de razón de verosimilitud junto con su generalización, la verosimilitud relativa.