Cúpula triangular giroelongada

En geometría, la cúpula triangular giroelongada es uno de los sólidos de Johnson (J₂₂). Se puede construir uniendo un antiprisma hexagonal a la base de una cúpula triangular (J₃). Esto se llama "giroelongación", lo que significa que un antiprisma se une a la base de un sólido, o entre las bases de más de un sólido.

La cúpula triangular giroelongada también se puede ver como una bicúpula triangular giroelongada (J₄₄) a la que se le ha quitado una cúpula triangular. Como todas las cúpulas, el polígono base tiene el doble de lados que el polígono superior (en este caso, el polígono inferior es un hexágono porque el superior es un triángulo).

Un sólido de Johnson es uno de los 92 poliedros estrictamente convexos que se componen de caras de polígonos regulares pero que no son poliedros uniformes (es decir, no son sólidos platónicos, sólidos de Arquímedes, prismas o antiprismas). Fueron nombrados por Norman Johnson, quien enumeró estos poliedros por primera vez en 1966.

Fórmulas

Las siguientes fórmulas para volumen y área de superficie se pueden usar si todas las caras son regulares, con una longitud de borde a:

V=()13612+183+301+3)a3.. 3.51605...a3{displaystyle V=left({frac {1}{3}}{sqrt {frac {61}{2}}+18{sqrt {3}}+30{sqrt {1+{sqrt {3}}}}}}right)a^{3}approx 3.51605...a^{3}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}}}sq}}}}sq}}}}}sq}}sq}}sq}}sq}sq}}}sq}}}}}sq}sq}sq}sq}sq}sq}sq}}sq}sq}}sq}}sq}sq}sq}}}}}}}}}}}}}}}sq}}}sq}}}}sq}}}}}}}}}sq

A=()3+1132)a2.. 12.5263...a2{displaystyle A=left(3+{frac {11{sqrt {3}}{2}right)a}approx 12.5263...a^{2}

Poliedro dual

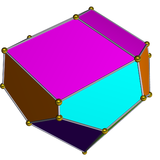
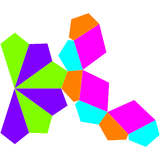
El dual de la cúpula triangular giroelongada tiene 15 caras: 6 cometas, 3 rombos y 6 pentágonos.

Dual glyroelongated triangular cupola	Net of dual