Cuadratura gaussiana

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Aproximación de la parte integral definida de una función

Comparación entre cuadratura Gaussiana de 2 puntos y trapezoidal.
La curva azul muestra la función cuya integral definida en el intervalo

[1, a 1]

se calculará (el integrado). La regla trapezoidal aproxima la función con una función lineal que coincide con el integrado en los extremos del intervalo y está representada por una línea desgarrada de naranja. La aproximación no es aparentemente buena, por lo que el error es grande (la regla trapezoidal da aproximación de la integral igual a

Sí. (-1) + Sí. (1) = -10

, mientras que el valor correcto es

2.3

). Para obtener un resultado más exacto, el intervalo debe dividirse en muchas subintervalaciones y luego composite debe usarse la regla trapezoidal, que requiere mucho más cálculos.
La cuadrícula gausiana elige puntos más adecuados en su lugar, por lo que incluso una función lineal aproxima mejor la función (la línea negra desgarrada). Como el integrado es el polinomio del grado 3 (

Sí. () x) = 7 x 3 - 8 x 2 - 3 x + 3

), la regla de cuadratura Gaussiana de 2 puntos incluso devuelve un resultado exacto.

En el análisis numérico, una regla de cuadratura es una aproximación de la integral definida de una función, generalmente expresada como una suma ponderada de los valores de la función en puntos específicos dentro del dominio de integración. (Consulte la integración numérica para obtener más información sobre las reglas de cuadratura). después de Carl Friedrich Gauss, es una regla de cuadratura construida para producir un resultado exacto para polinomios de grado $2 n - 1$ o menos mediante una elección adecuada de la nodos $x i$ y pesos $w i$ para $i = 1, \dots, n$ . Carl Gustav Jacobi desarrolló la formulación moderna que usa polinomios ortogonales en 1826. El dominio de integración más común para tal regla se toma como $[-1, 1]$ , por lo que la regla se declara como

{displaystyle int _{-1}^{1}f(x),dxapprox sum _{i=1}^{n}w_{i}f(x_{i}),}

que es exacto para polinomios de grado $2 n - 1$ o menos. Esta regla exacta se conoce como la regla de cuadratura de Gauss-Legendre. La regla de cuadratura solo será una aproximación precisa a la integral anterior si $f (x)$ está bien aproximado por un polinomio de grado $2 n - 1$ o menos en $[-1, 1]$ .

La regla de cuadratura de Gauss-Legendre no suele usarse para funciones integrables con singularidades de punto final. En cambio, si el integrando se puede escribir como

-1,}" xmlns="http://www.w3.org/1998/Math/MathML">f()x)=()1− − x)α α ()1+x)β β g()x),α α ,β β ■− − 1,{displaystyle f(x)=left(1-xright)^{alpha }left(1+xright)^{beta }g(x),quad alphabeta - No.-1,}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/14d153cd88aca586ec1dfd9818995b3054e3c6b0" style="vertical-align: -0.838ex; width:42.439ex; height:3.343ex;"/>

donde $g (x)$ está bien aproximado por un polinomio de bajo grado, entonces los nodos alternativos $x i'$ y pesos $w i'$ generalmente proporcionará reglas de cuadratura más precisas. Estas se conocen como reglas de cuadratura de Gauss-Jacobi, es decir,

{displaystyle int _{-1}^{1}f(x),dx=int _{-1}^{1}left(1-xright)^{alpha }left(1+xright)^{beta }g(x),dxapprox sum _{i=1}^{n}w_{i}'gleft(x_{i}'right).}

Los pesos comunes incluyen ${textstyle {frac {1}{sqrt {1-x^{2}}}}}$ (Chebyshev-Gauss) y ${sqrt {1-x^{2}}}$ . También es posible que desee integrarse sobre los intervalos semiinfinitos (cuadratura de Gauss-Laguerre) e infinitos (cuadradura de gauss–Hermite).

Se puede demostrar (ver Press, et al., o Stoer y Bulirsch) que los nodos de cuadratura $x i$ son las raíces de un polinomio que pertenece a una clase de polinomios ortogonales (la clase ortogonal con respecto a un producto interno ponderado). Esta es una observación clave para calcular los nodos y pesos en cuadratura de Gauss.

Gauss-Cuadratura Legendre

Gráficos de polinomios legendarios (hasta

n 5)

Para el problema de integración más simple indicado anteriormente, es decir, $f () x)$ está bien aproximado por polinomios en $[-1, 1]$ , los polinomios ortogonales asociados son polinomios Legendre, denotados por $P n () x)$ . Con la $n$ -th polinomial normalizado para dar $P n (1) = 1$ , el $i$ - El nodo Gauss, $x i$ , es el $i$ -la raíz de $P n$ y los pesos son dados por la fórmula (Abramowitz " Stegun 1972, p. 887) harv error: no target: CITEREFAbramowitzStegun1972 (help)

{displaystyle w_{i}={frac {2}{left(1-x_{i}^{2}right)left[P'_{n}(x_{i})right]^{2}}}.}

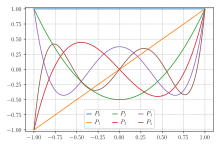
Algunas reglas de cuadratura de orden bajo se tabulan a continuación (sobre el intervalo $[-1, 1]$ , consulte la sección a continuación para conocer otros intervalos).

Número de puntos, n	Puntos, $x i$		Pesos, $w i$
1	0		2
2	${displaystyle pm {frac {1}{sqrt {3}}}}$	±0.57735...	1
3	0		${displaystyle {frac {8}{9}}}$	0.888889...
3	${displaystyle pm {sqrt {frac {3}{5}}}}$	±0.774597...	${displaystyle {frac {5}{9}}}$	0.555556...
4	${displaystyle pm {sqrt {{frac {3}{7}}-{frac {2}{7}}{sqrt {frac {6}{5}}}}}}$	±0.339981...	${displaystyle {frac {18+{sqrt {30}}}{36}}}$	0.652145...
4	${displaystyle pm {sqrt {{frac {3}{7}}+{frac {2}{7}}{sqrt {frac {6}{5}}}}}}$	±0.861136...	${displaystyle {frac {18-{sqrt {30}}}{36}}}$	0.347855...
5	0		${displaystyle {frac {128}{225}}}$	0.568889...
	${displaystyle pm {frac {1}{3}}{sqrt {5-2{sqrt {frac {10}{7}}}}}}$	±0.538469...	${displaystyle {frac {322+13{sqrt {70}}}{900}}}$	0.478629...
	${displaystyle pm {frac {1}{3}}{sqrt {5+2{sqrt {frac {10}{7}}}}}}$	±0.90618...	${displaystyle {frac {322-13{sqrt {70}}}{900}}}$	0.236927...

Cambio de intervalo

Una integral sobre $[a, b]$ debe cambiarse a una integral sobre $[-1, 1]$ antes de aplicar la regla de cuadratura de Gauss. Este cambio de intervalo se puede realizar de la siguiente forma:

{displaystyle int _{a}^{b}f(x),dx=int _{-1}^{1}fleft({frac {b-a}{2}}xi +{frac {a+b}{2}}right),{frac {dx}{dxi }}dxi }

con ${displaystyle {frac {dx}{dxi }}={frac {b-a}{2}}}$

Aplicar el $n$ punto cuadratura Gausiana ${displaystyle (xiw)}$ regla entonces resulta en la siguiente aproximación:

{displaystyle int _{a}^{b}f(x),dxapprox {frac {b-a}{2}}sum _{i=1}^{n}w_{i}fleft({frac {b-a}{2}}xi _{i}+{frac {a+b}{2}}right).}

Ejemplo de regla de cuadratura de Gauss de dos puntos

Utilice la regla de cuadrícula de dos puntos Gauss para aproximar la distancia en metros cubiertos por un cohete desde ${displaystyle t=8mathrm {s} }$ a ${displaystyle t=30mathrm {s}}$ por el Secretario General

{displaystyle x=int _{8}^{30}{left(2000ln left[{frac {140000}{140000-2100t}}right]-9.8tright){dt}}}

Cambie los límites para que se puedan usar los pesos y abscisas dados en la Tabla 1. Además, encuentre el error verdadero relativo absoluto. El valor verdadero se da como 11061.34 m.

Solución

Primero, cambiar los límites de la integración ${displaystyle left[8,30right]}$ a ${displaystyle left[-1,1right]}$ da

{displaystyle {begin{aligned}int _{8}^{30}{f(t)dt}&={frac {30-8}{2}}int _{-1}^{1}{fleft({frac {30-8}{2}}x+{frac {30+8}{2}}right){dx}}\&=11int _{-1}^{1}{fleft(11x+19right){dx}}end{aligned}}}

A continuación, obtenga los factores de ponderación y los valores de los argumentos de función de la Tabla 1 para la regla de los dos puntos,

${displaystyle c_{1}=1.000000000}$
${displaystyle x_{1}=-0.577350269}$
${displaystyle c_{2}=1.000000000}$
${displaystyle x_{2}=0.577350269}$

Ahora podemos usar la fórmula de cuadratura de Gauss

{displaystyle {begin{aligned}11int _{-1}^{1}{fleft(11x+19right){dx}}&approx 11left[c_{1}fleft(11x_{1}+19right)+c_{2}fleft(11x_{2}+19right)right]\&=11left[fleft(11(-0.5773503)+19right)+fleft(11(0.5773503)+19right)right]\&=11left[f(12.64915)+f(25.35085)right]\&=11left[(296.8317)+(708.4811)right]\&=11058.44end{aligned}}}

{displaystyle {begin{aligned}f(12.64915)&=2000ln left[{frac {140000}{140000-2100(12.64915)}}right]-9.8(12.64915)\&=296.8317end{aligned}}}

{displaystyle {begin{aligned}f(25.35085)&=2000ln left[{frac {140000}{140000-2100(25.35085)}}right]-9.8(25.35085)\&=708.4811end{aligned}}}

Dado que el valor verdadero es 11061.34 m, el error absoluto relativo verdadero, ${displaystyle left|varepsilon _{t}right|}$ es

{displaystyle left|varepsilon _{t}right|=left|{frac {11061.34-11058.44}{11061.34}}right|times 100%=0.0262%}

Otras formas

El problema de integración se puede expresar de una manera un poco más general introduciendo una función de peso positivo $ω$ en el integrando, y permitiendo un intervalo que no sea $[-1, 1]$ . Es decir, el problema es calcular

int _{a}^{b}omega (x),f(x),dx

para algunas opciones de $a$ , $b$ y $ω$ . Para $a = -1$ , $b = 1$ y $ω(x) = 1$ , el problema es el mismo que el considerado anteriormente. Otras opciones conducen a otras reglas de integración. Algunos de estos se tabulan a continuación. Se dan números de ecuación para Abramowitz y Stegun (A & S).

Interval	$\cdot () x)$	Polinomios ortogonales	A ' S	Para más información, vea...
$[1, a 1]$	$1$	Polinomios legendarios	25.4.29	§ Gauss–Legendre quadrature
$(1, 1)$	$-1}" xmlns="http://www.w3.org/1998/Math/MathML">()1− − x)α α ()1+x)β β ,α α ,β β ■− − 1{displaystyle left(1-xright)^{alpha }left(1+xright)^{beta },quad alphabeta.-1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d7eaa9834b96d1af1950a47ebdd00e0942332978" style="vertical-align: -0.838ex; width:30.021ex; height:3.343ex;"/>$	Jacobi polinomials	25.4.33 (continuación) $β = 0$ )	Cuadradura de Gauss–Jacobi
$(1, 1)$	${frac {1}{sqrt {1-x^{2}}}}$	Polinomios Chebyshev (primer tipo)	25.4.38	Chebyshev-Gauss quadrature
$[1, a 1]$	${sqrt {1-x^{2}}}$	Polinomios Chebyshev (segundo tipo)	25.4.40	Chebyshev-Gauss quadrature
$[0, \infty]$	$e^{-x},$	Polinomios de Laguerre	25.4.45	Cuadradura de Gauss–Laguerre
$[0, \infty]$	$-1}" xmlns="http://www.w3.org/1998/Math/MathML">xα α e− − x,α α ■− − 1{displaystyle x^{alpha }e^{-x},quad alpha.-1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/804f03af0f8f5d59c16adafa17d5e8bc6b95adee" style="vertical-align: -0.671ex; width:17.062ex; height:2.843ex;"/>$	Polinomios de Laguerre generalizados		Cuadradura de Gauss–Laguerre
$(Libertad, \infty)$	$e^{-x^{2}}$	Polinomios hermitas	25.4.46	Cuadradura de Gauss–Hermite

Teorema fundamental

Sea $p n$ un polinomio no trivial de grado $n$ tal que

{displaystyle int _{a}^{b}omega (x),x^{k}p_{n}(x),dx=0,quad {text{for all }}k=0,1,ldotsn-1.}

Tenga en cuenta que esto será cierto para todos los polinomios ortogonales anteriores, porque cada $p n$ se construye para ser ortogonal a los otros polinomios $p j$ para $j < n$ y $x k$ está en el lapso de ese conjunto.

Si elegimos los $n$ nodos $x i$ para ser los ceros de $p n$ , entonces existen $n$ pesos $w i$ que hacen que la integral calculada en cuadratura de Gauss sea exacta para todos los polinomios $h (x)$ de grado $2 n - 1$ o menos. Además, todos estos nodos $x i$ estarán en el intervalo abierto $(a, b)$ (Stoer & Bulirsch 2002, págs. 172–175).

Para probar la primera parte de esta afirmación, sea $h (x)$ cualquier polinomio de grado $2 n - 1$ o menos. Divídalo por el polinomio ortogonal $p n$ para obtener

{displaystyle h(x)=p_{n}(x),q(x)+r(x).}

donde $q (x)$ es el cociente, de grado $n - 1$ o menos (porque la suma de su grado y la del divisor $p n$ debe ser igual al del dividendo), y $r (x)$ es el resto, también de grado $n - 1$ o menor (porque el grado del resto siempre es menor que el del divisor). Dado que $p n$ es por suposición ortogonal a todos los monomios de grado menor que $n$ , debe ser ortogonal al cociente $q (x)$ . Por lo tanto

{displaystyle int _{a}^{b}omega (x),h(x),dx=int _{a}^{b}omega (x),{big (},p_{n}(x)q(x)+r(x),{big)},dx=int _{a}^{b}omega (x),r(x),dx.}

Dado que el resto $r (x)$ es de grado $n - 1$ o menos, podemos interpolarlo exactamente usando $n$ puntos de interpolación con polinomios de Lagrange l_i(x), donde

{displaystyle l_{i}(x)=prod _{jneq i}{frac {x-x_{j}}{x_{i}-x_{j}}}.}

Tenemos

{displaystyle r(x)=sum _{i=1}^{n}l_{i}(x),r(x_{i}).}

Entonces su integral será igual

{displaystyle int _{a}^{b}omega (x),r(x),dx=int _{a}^{b}omega (x),sum _{i=1}^{n}l_{i}(x),r(x_{i}),dx=sum _{i=1}^{n},r(x_{i}),int _{a}^{b}omega (x),l_{i}(x),dx=sum _{i=1}^{n},r(x_{i}),w_{i},}

donde $w i$ , el peso asociado con el nodo $x i$ , se define para igualar la integral ponderada de $l i (x)$ (consulte a continuación otras fórmulas para los pesos). Pero todas las $x i$ son raíces de $p n$ , por lo que la fórmula de división anterior nos dice que

{displaystyle h(x_{i})=p_{n}(x_{i}),q(x_{i})+r(x_{i})=r(x_{i}),}

para todos los $i$ . Así finalmente tenemos

{displaystyle int _{a}^{b}omega (x),h(x),dx=int _{a}^{b}omega (x),r(x),dx=sum _{i=1}^{n}w_{i},r(x_{i})=sum _{i=1}^{n}w_{i},h(x_{i}).}

Esto prueba que para cualquier polinomio $h (x)$ de grado $2 n - 1$ o menos, su integral viene dada exactamente por la suma en cuadratura gaussiana.

Para probar la segunda parte de la afirmación, considere la forma factorizada del polinomio $p n$ . Cualquier raíz conjugada compleja producirá un factor cuadrático que es estrictamente positivo o estrictamente negativo sobre toda la línea real. Cualquier factor para raíces fuera del intervalo desde $a$ hasta $b$ no cambiará de signo durante ese intervalo. Finalmente, para los factores correspondientes a raíces $x i$ dentro del intervalo desde $a$ a $b$ que son de multiplicidad impar, multiplicar $p n$ por un factor más para hacer un nuevo polinomio

{displaystyle p_{n}(x),prod _{i}(x-x_{i}).}

Este polinomio no puede cambiar de signo en el intervalo de $a$ a $b$ porque todas sus raíces ahora son incluso multiplicidad. Entonces la integral

{displaystyle int _{a}^{b}p_{n}(x),left(prod _{i}(x-x_{i})right),omega (x),dxneq 0,}

ya que la función de peso $ω (x)$ siempre es no negativa. Pero $p n$ es ortogonal a todos los polinomios de grado <span class="texhtml" n-1 o menos, por lo que el grado del producto

{displaystyle prod _{i}(x-x_{i})}

debe ser al menos $n$ . Por lo tanto $p n$ tiene $n$ raíces distintas, todas reales, en el intervalo de $a$ a b.

Fórmula general para los pesos

Los pesos se pueden expresar como

{displaystyle w_{i}={frac {a_{n}}{a_{n-1}}}{frac {int _{a}^{b}omega (x)p_{n-1}left(xright)^{2}dx}{p'_{n}(x_{i})p_{n-1}(x_{i})}}}

()1)

Donde $a_{k}$ es el coeficiente de $x^{k}$ dentro $p_{k}(x)$ . Para probar esto, note que usando la interpolación de Lagrange uno puede expresar $r () x)$ en términos de $r(x_{i})$ como

r(x)=sum _{i=1}^{n}r(x_{i})prod _{begin{smallmatrix}1leq jleq n\jneq iend{smallmatrix}}{frac {x-x_{j}}{x_{i}-x_{j}}}

porque $r (x)$ tiene un grado menor que $n$ y, por lo tanto, está fijado por los valores que alcanza en $n$ puntos diferentes. Multiplicando ambos lados por $ω (x)$ e integrando desde $a$ a $b$ produce

int _{a}^{b}omega (x)r(x)dx=sum _{i=1}^{n}r(x_{i})int _{a}^{b}omega (x)prod _{begin{smallmatrix}1leq jleq n\jneq iend{smallmatrix}}{frac {x-x_{j}}{x_{i}-x_{j}}}dx

Los pesos $w i$ están dados por

w_{i}=int _{a}^{b}omega (x)prod _{begin{smallmatrix}1leq jleq n\jneq iend{smallmatrix}}{frac {x-x_{j}}{x_{i}-x_{j}}}dx

Esta expresión integral $w_{i}$ se puede expresar en términos de los polinomios ortogonales $p_{n}(x)$ y $p_{n-1}(x)$ como sigue.

Podemos escribir

prod _{begin{smallmatrix}1leq jleq n\jneq iend{smallmatrix}}left(x-x_{j}right)={frac {prod _{1leq jleq n}left(x-x_{j}right)}{x-x_{i}}}={frac {p_{n}(x)}{a_{n}left(x-x_{i}right)}}

Donde $a_{n}$ es el coeficiente de $x^{n}$ dentro $p_{n}(x)$ . Tomando el límite $x$ a $x_{i}$ rendimientos usando la regla de L'Hôpital

prod _{begin{smallmatrix}1leq jleq n\jneq iend{smallmatrix}}left(x_{i}-x_{j}right)={frac {p'_{n}(x_{i})}{a_{n}}}

Podemos escribir la expresión integral para los pesos como

w_{i}={frac {1}{p'_{n}(x_{i})}}int _{a}^{b}omega (x){frac {p_{n}(x)}{x-x_{i}}}dx

()2)

En el integrando, escribiendo

{displaystyle {frac {1}{x-x_{i}}}={frac {1-left({frac {x}{x_{i}}}right)^{k}}{x-x_{i}}}+left({frac {x}{x_{i}}}right)^{k}{frac {1}{x-x_{i}}}}

rendimientos

int _{a}^{b}omega (x){frac {x^{k}p_{n}(x)}{x-x_{i}}}dx=x_{i}^{k}int _{a}^{b}omega (x){frac {p_{n}(x)}{x-x_{i}}}dx

proporcionadas $kleq n$ , porque

{frac {1-left({frac {x}{x_{i}}}right)^{k}}{x-x_{i}}}

es un polinomio de grado $k - 1$ que es entonces ortogonal a $p_{n}(x)$ . Entonces, si $q () x)$ es un polinomio de la mayor parte del grado que tenemos

int _{a}^{b}omega (x){frac {p_{n}(x)}{x-x_{i}}}dx={frac {1}{q(x_{i})}}int _{a}^{b}omega (x){frac {q(x)p_{n}(x)}{x-x_{i}}}dx

Podemos evaluar la integral en el lado derecho para $q(x)=p_{n-1}(x)$ como sigue. Porque... ${frac {p_{n}(x)}{x-x_{i}}}$ es un polinomio de grado $n - 1$ , tenemos

{frac {p_{n}(x)}{x-x_{i}}}=a_{n}x^{n-1}+s(x)

Donde $s () x)$ es un polinomio de grado $n - 2$ . Desde $s () x)$ es ortogonal a $p_{n-1}(x)$ tenemos

int _{a}^{b}omega (x){frac {p_{n}(x)}{x-x_{i}}}dx={frac {a_{n}}{p_{n-1}(x_{i})}}int _{a}^{b}omega (x)p_{n-1}(x)x^{n-1}dx

Entonces podemos escribir

x^{n-1}=left(x^{n-1}-{frac {p_{n-1}(x)}{a_{n-1}}}right)+{frac {p_{n-1}(x)}{a_{n-1}}}

El término entre corchetes es un polinomio de grado $n - 2$ , que es ortogonal a $p_{n-1}(x)$ . La integral puede ser escrita como

int _{a}^{b}omega (x){frac {p_{n}(x)}{x-x_{i}}}dx={frac {a_{n}}{a_{n-1}p_{n-1}(x_{i})}}int _{a}^{b}omega (x)p_{n-1}(x)^{2}dx

Según la ecuación (2), los pesos se obtienen dividiendo esto por $p'_{n}(x_{i})$ y que produce la expresión en la ecuación (1).

$w_{i}$ también se puede expresar en términos de los polinomios ortogonales $p_{n}(x)$ y ahora $p_{n+1}(x)$ . En la relación de recurrencia de 3 plazos ${displaystyle p_{n+1}(x_{i})=(a)p_{n}(x_{i})+(b)p_{n-1}(x_{i})}$ el término con ${displaystyle p_{n}(x_{i})}$ desaparece, así que ${displaystyle p_{n-1}(x_{i})}$ en Eq. (1) puede ser reemplazado por ${textstyle {frac {1}{b}}p_{n+1}left(x_{i}right)}$ .

Prueba de que los pesos son positivos

Considerar el siguiente polinomio de grado ${displaystyle 2n-2}$

{displaystyle f(x)=prod _{begin{smallmatrix}1leq jleq n\jneq iend{smallmatrix}}{frac {left(x-x_{j}right)^{2}}{left(x_{i}-x_{j}right)^{2}}}}

donde, como se ha indicado anteriormente, $x j$ son las raíces del polinomio $p_{n}(x)$ . Claramente ${displaystyle f(x_{j})=delta _{ij}}$ . Desde el grado de $f(x)$ es menos que $2n-1$ , la fórmula de cuadrícula Gausiana que implica los pesos y nodos obtenidos de $p_{n}(x)$ Se aplica. Desde ${displaystyle f(x_{j})=0}$ por j no igual a mí, tenemos

0.}" xmlns="http://www.w3.org/1998/Math/MathML">∫ ∫ ab⋅ ⋅ ()x)f()x)dx=.. j=1nwjf()xj)=.. j=1nδ δ ijwj=wi■0.{displaystyle int _{a}^{b}omega (x)f(x)dx=sum _{j=1}^{n}w_{j}f(x_{j})=sum - ¿Por qué? ¿Qué?0.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b91798b9f2426e443db17715df4411e19c270b9d" style="vertical-align: -3.338ex; width:52.472ex; height:7.343ex;"/>

Desde ambos $omega (x)$ y $f(x)$ son funciones no negativas, de ahí que $0}" xmlns="http://www.w3.org/1998/Math/MathML">wi■0{displaystyle ¿Qué?0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ae83301aafa900ab58d3d6b84589d97653824986" style="vertical-align: -0.671ex; width:6.725ex; height:2.509ex;"/>$ .

Cálculo de las reglas de cuadratura gaussiana

Hay muchos algoritmos para calcular los nodos $x i$ y pesos $w i$ de reglas de cuadratura gausiana. Los más populares son el algoritmo Golub-Welsch que requiere $O () n 2)$ operaciones, método de Newton para resolver ${displaystyle p_{n}(x)=0}$ utilizando la recurrencia de tres plazos para la evaluación necesaria $O () n 2)$ operaciones, y fórmulas asintoticas para grandes n necesidad $O () n)$ operaciones.

Relación de recurrencia

Polinomios ortogonales $p_{r}$ con ${displaystyle (p_{r},p_{s})=0}$ para ${displaystyle rneq s}$ para un producto de cuero ${displaystyle (,,)}$ , grado ${displaystyle (p_{r})=r}$ y el coeficiente líder uno (es decir, polinomios ortogonales monicos) satisfacen la relación de recurrencia

{displaystyle p_{r+1}(x)=(x-a_{r,r})p_{r}(x)-a_{r,r-1}p_{r-1}(x)cdots -a_{r,0}p_{0}(x)}

y producto escalar definido

{displaystyle (f(x),g(x))=int _{a}^{b}omega (x)f(x)g(x)dx}

para ${displaystyle r=0,1,ldotsn-1}$ Donde $n$ es el grado máximo que se puede tomar para ser infinito, y donde ${textstyle a_{r,s}={frac {left(xp_{r},p_{s}right)}{left(p_{s},p_{s}right)}}}$ . En primer lugar, los polinomios definidos por la relación recurrencia comenzando con ${displaystyle p_{0}(x)=1}$ tienen un coeficiente líder y un grado correcto. Dado el punto de partida por $p_{0}$ , la ortogonalidad de $p_{r}$ se puede mostrar por inducción. Para ${displaystyle r=s=0}$ uno tiene

{displaystyle (p_{1},p_{0})=(x-a_{0,0})(p_{0},p_{0})=(xp_{0},p_{0})-a_{0,0}(p_{0},p_{0})=(xp_{0},p_{0})-(xp_{0},p_{0})=0.}

Ahora si ${displaystyle p_{0},p_{1},ldotsp_{r}}$ son ortogonales, entonces también $p_{r+1}$ , porque dentro

{displaystyle (p_{r+1},p_{s})=(xp_{r},p_{s})-a_{r,r}(p_{r},p_{s})-a_{r,r-1}(p_{r-1},p_{s})cdots -a_{r,0}(p_{0},p_{s})}

todos los productos de escalar desaparecen excepto el primero y el uno donde $p_{s}$ conoce el mismo polinomio ortogonal. Por lo tanto,

(p_{r+1},p_{s})=(xp_{r},p_{s})-a_{r,s}(p_{s},p_{s})=(xp_{r},p_{s})-(xp_{r},p_{s})=0.

Sin embargo, si el producto scalar satisfies ${displaystyle (xf,g)=(f,xg)}$ (que es el caso de la cuadratura gausiana), la relación recurrencia reduce a una relación de recurrencia de tres plazos: Para $<math alttext="{displaystyle ss.r- - 1,xps{displaystyle [S] <img alt="{displaystyle s$ es un polinomio de grado inferior o igual a $r - 1$ . Por otro lado, $p_{r}$ es ortogonal a cada polinomio de grado inferior o igual a $r - 1$ . Por lo tanto, uno tiene ${displaystyle (xp_{r},p_{s})=(p_{r},xp_{s})=0}$ y ${displaystyle a_{r,s}=0}$ para $s . r - 1$ . La relación de recurrencia entonces simplifica

p_{r+1}(x)=(x-a_{r,r})p_{r}(x)-a_{r,r-1}p_{r-1}(x)

p_{r+1}(x)=(x-a_{r})p_{r}(x)-b_{r}p_{r-1}(x)

(con la convención) ${displaystyle p_{-1}(x)equiv 0}$ Donde

a_{r}:={frac {(xp_{r},p_{r})}{(p_{r},p_{r})}},qquad b_{r}:={frac {(xp_{r},p_{r-1})}{(p_{r-1},p_{r-1})}}={frac {(p_{r},p_{r})}{(p_{r-1},p_{r-1})}}

(el último debido a ${displaystyle (xp_{r},p_{r-1})=(p_{r},xp_{r-1})=(p_{r},p_{r})}$ , desde $xp_{r-1}$ difiere de $p_{r}$ por un grado inferior $r$ ).

El algoritmo de Golub-Welsch

La relación de recurrencia de tres plazos se puede escribir en forma de matriz ${displaystyle J{tilde {P}}=x{tilde {P}}-p_{n}(x)times mathbf {e} _{n}}$ Donde ${displaystyle {tilde {P}}={begin{bmatrix}p_{0}(x)&p_{1}(x)&ldots &p_{n-1}(x)end{bmatrix}}^{mathsf {T}}}$ , $mathbf {e} _{n}$ es $n$ vector de base estándar, es decir, ${displaystyle mathbf {e} _{n}={begin{bmatrix}0&ldots &0&1end{bmatrix}}^{mathsf {T}}}$ , y $J$ es la llamada matriz Jacobi:

{displaystyle mathbf {J} ={begin{pmatrix}a_{0}&1&0&ldots &ldots &ldots \b_{1}&a_{1}&1&0&ldots &ldots \0&b_{2}&a_{2}&1&0&ldots \0&ldots &ldots &ldots &ldots &0\ldots &ldots &0&b_{n-2}&a_{n-2}&1\ldots &ldots &ldots &0&b_{n-1}&a_{n-1}end{pmatrix}}}

Los ceros $x_{j}$ de los polinomios hasta el grado $n$ , que se utilizan como nodos para la cuadratura gausiana se puede encontrar computando los eigenvalues de esta matriz tridiagonal. Este procedimiento se conoce como algoritmo de golub–Welsch.

Para calcular los pesos y los nodos, es preferible considerar la matriz tridiagonal simétrica ${mathcal {J}}$ con elementos

{displaystyle {begin{aligned}{mathcal {J}}_{i,i}=J_{i,i}&=a_{i-1}&&i=1,ldotsn\{mathcal {J}}_{i-1,i}={mathcal {J}}_{i,i-1}={sqrt {J_{i,i-1}J_{i-1,i}}}&={sqrt {b_{i-1}}}&&i=2,ldotsn.end{aligned}}}

$J$ y ${mathcal {J}}$ son matrices similares y por lo tanto tienen los mismos eigenvalues (los nodos). Los pesos se pueden calcular de los eigenvectores correspondientes: Si $phi ^{(j)}$ es un eigenvector normalizado (es decir, un eigenvector con norma euclidiana igual a uno) asociado al eigenvalue $x j$ , el peso correspondiente se puede calcular desde el primer componente de este eigenvector, a saber:

w_{j}=mu _{0}left(phi _{1}^{(j)}right)^{2}

Donde $mu _{0}$ es la parte integral de la función de peso

mu _{0}=int _{a}^{b}omega (x)dx.

Ver, por ejemplo, (Gil, Segura & Temme 2007) para más detalles.

Estimaciones de errores

El error de una regla de cuadratura gaussiana se puede establecer de la siguiente manera (Stoer & Bulirsch 2002, Thm 3.6.24). Para un integrando que tiene $2 n$ derivadas continuas,

{displaystyle int _{a}^{b}omega (x),f(x),dx-sum _{i=1}^{n}w_{i},f(x_{i})={frac {f^{(2n)}(xi)}{(2n)!}},(p_{n},p_{n})}

para algunos $ξ$ en $(a, b)$ , donde $p n$ es el mónico (es decir, el coeficiente principal es $1$ ) polinomio ortogonal de grado $n$ y donde

(f,g)=int _{a}^{b}omega (x)f(x)g(x),dx.

En el importante caso especial de $ω (x) = 1$ , tenemos la estimación del error (Kahaner, Moler & Nash 1989, §5.2)

<math alttext="{displaystyle {frac {left(b-aright)^{2n+1}left(n!right)^{4}}{(2n+1)left[left(2nright)!right]^{3}}}f^{(2n)}(xi),qquad a<xi ()b− − a)2n+1()n!)4()2n+1)[()2n)!]3f()2n)().. ),a... .b.{displaystyle {frac {left(b-aright)^{2n+1}left(n!right)}{4}}{(2n+1)left[left(2nright)!right]^{3}f^{(2n)}(xi),qquad a truexi.}<img alt="{displaystyle {frac {left(b-aright)^{2n+1}left(n!right)^{4}}{(2n+1)left[left(2nright)!right]^{3}}}f^{(2n)}(xi),qquad a<xi

Stoer y Bulirsch comentan que esta estimación de error es inconveniente en la práctica, ya que puede ser difícil estimar la derivada de orden $2 n$ , y además el error real puede ser mucho menor que un límite establecido por la derivada. Otro enfoque es usar dos reglas de cuadratura gaussiana de diferentes órdenes y estimar el error como la diferencia entre los dos resultados. Para este propósito, las reglas de cuadratura de Gauss-Kronrod pueden ser útiles.

Reglas de Gauss-Kronrod

Si el intervalo $[a, b]$ se subdivide, los puntos de evaluación de Gauss de los nuevos subintervalos nunca coinciden con los puntos de evaluación anteriores (excepto en cero para números impares), por lo que el integrando debe evaluarse en cada punto. Las reglas de Gauss-Kronrod son extensiones de las reglas de cuadratura de Gauss generadas al agregar $n + 1$ puntos a una $n$ -punto regla de tal manera que la regla resultante sea de orden $2 n + 1$ . Esto permite calcular estimaciones de orden superior mientras se reutilizan los valores de función de una estimación de orden inferior. La diferencia entre una regla de cuadratura de Gauss y su extensión de Kronrod se usa a menudo como una estimación del error de aproximación.

Reglas de Gauss-Lobatto

También conocida como cuadratura de Lobatto (Abramowitz & Stegun 1972, p. 888) error de harv: sin objetivo: CITEREFAbramowitzStegun1972 (ayuda), llamado así por el matemático holandés Rehuel Lobatto. Es similar a la cuadratura gaussiana con las siguientes diferencias:

Los puntos de integración incluyen los puntos finales del intervalo de integración.
Es preciso para polinomios hasta cierto grado $2 n - 3$ , donde $n$ es el número de puntos de integración (Quarteroni, Sacco & Saleri 2000).

Lobatto cuadratura de la función $f (x)$ en el intervalo $[-1, 1]$ :

${displaystyle int _{-1}^{1}{f(x),dx}={frac {2}{n(n-1)}}[f(1)+f(-1)]+sum _{i=2}^{n-1}{w_{i}f(x_{i})}+R_{n}.}$

Abscissas: $x i$ es $(i - 1)$ st cero de $P'_{n-1}(x)$ , Aquí. ${displaystyle P_{m}(x)}$ denota el polinomio estándar Legendre de m-th grado y el dash denota el derivativo.

Pesos:

${displaystyle w_{i}={frac {2}{n(n-1)left[P_{n-1}left(x_{i}right)right]^{2}}},qquad x_{i}neq pm 1.}$

Restante:

$<math alttext="{displaystyle R_{n}={frac {-nleft(n-1right)^{3}2^{2n-1}left[left(n-2right)!right]^{4}}{(2n-1)left[left(2n-2right)!right]^{3}}}f^{(2n-2)}(xi),qquad -1<xi Rn=− − n()n− − 1)322n− − 1[()n− − 2)!]4()2n− − 1)[()2n− − 2)!]3f()2n− − 2)().. ),− − 1... .1.{displaystyle R_{n}={frac {-nright)}{3}2^{2n-1}left[left(n-2right)}right]}{4}{4}{(2n-1)left[left(2n-2qright)}right]} {3}}} {(2n-2)}dxi),1}q].<img alt="{displaystyle R_{n}={frac {-nleft(n-1right)^{3}2^{2n-1}left[left(n-2right)!right]^{4}}{(2n-1)left[left(2n-2right)!right]^{3}}}f^{(2n-2)}(xi),qquad -1<xi$

Algunos de los pesos son:

Número de puntos, n	Puntos, $x i$	Pesos, $w i$
$3$	${displaystyle 0}$	${frac {4}{3}}$
$3$	$pm 1$	${frac {1}{3}}$
$4$	${displaystyle pm {sqrt {frac {1}{5}}}}$	${frac {5}{6}}$
$4$	$pm 1$	${frac {1}{6}}$
$5$	${displaystyle 0}$	${frac {32}{45}}$
	${displaystyle pm {sqrt {frac {3}{7}}}}$	${frac {49}{90}}$
	$pm 1$	${frac {1}{10}}$
$6$	${displaystyle pm {sqrt {{frac {1}{3}}-{frac {2{sqrt {7}}}{21}}}}}$	${displaystyle {frac {14+{sqrt {7}}}{30}}}$
	${displaystyle pm {sqrt {{frac {1}{3}}+{frac {2{sqrt {7}}}{21}}}}}$	${displaystyle {frac {14-{sqrt {7}}}{30}}}$
	$pm 1$	${displaystyle {frac {1}{15}}}$
$7$	${displaystyle 0}$	${displaystyle {frac {256}{525}}}$
	${displaystyle pm {sqrt {{frac {5}{11}}-{frac {2}{11}}{sqrt {frac {5}{3}}}}}}$	${displaystyle {frac {124+7{sqrt {15}}}{350}}}$
	${displaystyle pm {sqrt {{frac {5}{11}}+{frac {2}{11}}{sqrt {frac {5}{3}}}}}}$	${displaystyle {frac {124-7{sqrt {15}}}{350}}}$
	$pm 1$	${displaystyle {frac {1}{21}}}$