Correspondencia AdS/CFT

En física teórica, la correspondencia anti-de Sitter/teoría de campos conforme (frecuentemente abreviada como AdS/CFT) es una relación conjeturada entre dos tipos de teorías físicas. Por un lado están los espacios anti-de Sitter (AdS) que se utilizan en las teorías de la gravedad cuántica, formuladas en términos de teoría de cuerdas o teoría M. En el otro lado de la correspondencia están las teorías de campos conformes (CFT), que son teorías cuánticas de campos, incluidas teorías similares a las teorías de Yang-Mills que describen partículas elementales.

La dualidad representa un avance importante en la comprensión de la teoría de cuerdas y la gravedad cuántica. Esto se debe a que proporciona una formulación no perturbativa de la teoría de cuerdas con ciertas condiciones límite y a que es la realización más exitosa del principio holográfico, una idea de la gravedad cuántica propuesta originalmente por Gerard 't Hooft y promovida por Leonard Susskind. .

También proporciona un potente conjunto de herramientas para estudiar teorías de campos cuánticos fuertemente acoplados. Gran parte de la utilidad de la dualidad resulta del hecho de que es una dualidad fuerte-débil: cuando los campos de la teoría cuántica de campos interactúan fuertemente, los de la teoría gravitacional interactúan débilmente y, por tanto, son más manejables matemáticamente. Este hecho se ha utilizado para estudiar muchos aspectos de la física nuclear y de la materia condensada traduciendo problemas de esas materias en problemas más manejables matemáticamente en la teoría de cuerdas.

La correspondencia AdS/CFT fue propuesta por primera vez por Juan Maldacena a finales de 1997. Pronto se elaboraron aspectos importantes de la correspondencia en dos artículos, uno de Steven Gubser, Igor Klebanov y Alexander Polyakov, y otro de Edward Witten. En 2015, el artículo de Maldacena tenía más de 10.000 citas, convirtiéndose en el artículo más citado en el campo de la física de altas energías. Para 2024, el artículo de Maldacena alcanzó más de 24.000 citas.

Uno de los ejemplos más destacados de la correspondencia AdS/CFT ha sido la correspondencia AdS5/CFT4: una relación entre N = 4 teoría supersimétrica de Yang-Mills en 3+1 dimensiones y la teoría de supercuerdas tipo IIB en AdS₅ × S⁵.

Fondo

Gravedad cuántica y cuerdas

La comprensión actual de la gravedad se basa en la teoría general de la relatividad de Albert Einstein. Formulada en 1915, la relatividad general explica la gravedad en términos de la geometría del espacio y el tiempo, o espaciotiempo. Está formulado en el lenguaje de la física clásica desarrollado por físicos como Isaac Newton y James Clerk Maxwell. Las demás fuerzas no gravitacionales se explican en el marco de la mecánica cuántica. Desarrollada en la primera mitad del siglo XX por varios físicos diferentes, la mecánica cuántica proporciona una forma radicalmente diferente de describir los fenómenos físicos basada en la probabilidad.

La gravedad cuántica es la rama de la física que busca describir la gravedad utilizando los principios de la mecánica cuántica. Actualmente, un enfoque popular de la gravedad cuántica es la teoría de cuerdas, que modela las partículas elementales no como puntos de dimensión cero sino como objetos unidimensionales llamados cuerdas. En la correspondencia AdS/CFT, normalmente se consideran teorías de la gravedad cuántica derivadas de la teoría de cuerdas o su extensión moderna, la teoría M.

En la vida cotidiana, existen tres dimensiones familiares de espacio (arriba/abajo, izquierda/derecha y adelante/atrás), y hay una dimensión de tiempo. Así, en el lenguaje de la física moderna, se dice que el espacio-tiempo es cuatridimensional. Una característica peculiar de la teoría de cuerdas y la teoría M es que estas teorías requieren dimensiones adicionales de espacio-tiempo para su consistencia matemática: en la teoría de cuerdas el espaciotiempo es de diez dimensiones, mientras que en la teoría M es de once dimensiones. Las teorías de la gravedad cuántica que aparecen en la correspondencia AdS/CFT se obtienen normalmente a partir de la teoría de cuerdas y M mediante un proceso conocido como compactificación. Esto produce una teoría en la que el espacio-tiempo tiene efectivamente un número menor de dimensiones y las dimensiones adicionales están "acurrucadas" en el espacio. en círculos.

Una analogía estándar para la compactación es considerar un objeto multidimensional como una manguera de jardín. Si la manguera se mira desde una distancia suficiente, parece tener una sola dimensión, su longitud, pero cuando uno se acerca a la manguera, descubre que contiene una segunda dimensión, su circunferencia. Así, una hormiga que se arrastrara en su interior se movería en dos dimensiones.

Teoría cuántica de campos

La aplicación de la mecánica cuántica a objetos físicos como el campo electromagnético, que se extienden en el espacio y el tiempo, se conoce como teoría cuántica de campos. En física de partículas, las teorías cuánticas de campos constituyen la base para nuestra comprensión de las partículas elementales, que se modelan como excitaciones en los campos fundamentales. Las teorías cuánticas de campos también se utilizan en toda la física de la materia condensada para modelar objetos similares a partículas llamados cuasipartículas.

En la correspondencia AdS/CFT, se considera, además de una teoría de la gravedad cuántica, un cierto tipo de teoría cuántica de campos llamada teoría de campos conforme. Este es un tipo de teoría cuántica de campos particularmente simétrica y matemáticamente bien comportada. Estas teorías se estudian a menudo en el contexto de la teoría de cuerdas, donde se asocian con la superficie barrida por una cuerda que se propaga a través del espacio-tiempo, y en la mecánica estadística, donde modelan sistemas en un punto crítico termodinámico.

Resumen de la correspondencia

Geometría del espacio anti-de Sitter

En la correspondencia AdS/CFT, se considera la teoría de cuerdas o la teoría M en un contexto anti-de Sitter. Esto significa que la geometría del espacio-tiempo se describe en términos de una determinada solución de vacío de la ecuación de Einstein llamada espacio anti-de Sitter.

En términos muy elementales, el espacio anti-de Sitter es un modelo matemático del espacio-tiempo en el que la noción de distancia entre puntos (la métrica) es diferente de la noción de distancia en la geometría euclidiana ordinaria. Está estrechamente relacionado con el espacio hiperbólico, que puede verse como un disco, como se ilustra a la derecha. Esta imagen muestra un mosaico de un disco formado por triángulos y cuadrados. Se puede definir la distancia entre los puntos de este disco de tal manera que todos los triángulos y cuadrados tengan el mismo tamaño y el límite exterior circular esté infinitamente lejos de cualquier punto del interior.

Ahora imagina una pila de discos hiperbólicos donde cada disco representa el estado del universo en un momento dado. El objeto geométrico resultante es un espacio tridimensional anti-de Sitter. Parece un cilindro sólido en el que cualquier sección transversal es una copia del disco hiperbólico. El tiempo corre en dirección vertical en esta imagen. La superficie de este cilindro juega un papel importante en la correspondencia AdS/CFT. Como ocurre con el plano hiperbólico, el espacio anti-de Sitter está curvado de tal manera que cualquier punto en el interior está en realidad infinitamente lejos de esta superficie límite.

Esta construcción describe un universo hipotético con sólo dos dimensiones espaciales y una temporal, pero se puede generalizar a cualquier número de dimensiones. De hecho, el espacio hiperbólico puede tener más de dos dimensiones y uno puede "apilar" varias dimensiones. copias del espacio hiperbólico para obtener modelos de dimensiones superiores del espacio anti-de Sitter.

Idea de AdS/CFT

Una característica importante del espacio anti-de Sitter es su límite (que parece un cilindro en el caso del espacio tridimensional anti-de Sitter). Una propiedad de este límite es que, localmente alrededor de cualquier punto, se parece al espacio de Minkowski, el modelo de espacio-tiempo utilizado en la física no gravitacional.

Por lo tanto, se puede considerar una teoría auxiliar en la que el "espaciotiempo" está dado por el límite del espacio anti-de Sitter. Esta observación es el punto de partida de la correspondencia AdS/CFT, que afirma que el límite del espacio anti-de Sitter puede considerarse como el "espaciotiempo" para una teoría de campos conforme. La afirmación es que esta teoría de campo conforme es equivalente a la teoría gravitacional en el espacio anti-de Sitter en el sentido de que existe un "diccionario" para traducir cálculos de una teoría en cálculos de la otra. Cada entidad en una teoría tiene una contraparte en la otra teoría. Por ejemplo, una sola partícula en la teoría gravitacional podría corresponder a algún conjunto de partículas en la teoría de límites. Además, las predicciones de las dos teorías son cuantitativamente idénticas, de modo que si dos partículas tienen un 40 por ciento de posibilidades de colisionar en la teoría gravitacional, entonces las colecciones correspondientes en la teoría de límites también tendrían un 40 por ciento de posibilidades de colisionar.

Observe que el límite del espacio anti-de Sitter tiene menos dimensiones que el propio espacio anti-de Sitter. Por ejemplo, en el ejemplo tridimensional ilustrado arriba, el límite es una superficie bidimensional. La correspondencia AdS/CFT a menudo se describe como una "dualidad holográfica" porque esta relación entre ambas teorías es similar a la relación entre un objeto tridimensional y su imagen en forma de holograma. Aunque un holograma es bidimensional, codifica información sobre las tres dimensiones del objeto que representa. De la misma manera, se conjetura que las teorías que están relacionadas por la correspondencia AdS/CFT son exactamente equivalentes, a pesar de vivir en diferentes números de dimensiones. La teoría de campos conforme es como un holograma que captura información sobre la teoría de la gravedad cuántica de dimensiones superiores.

Ejemplos de correspondencia

Siguiendo la idea de Maldacena en 1997, los teóricos han descubierto muchas realizaciones diferentes de la correspondencia AdS/CFT. Estos relacionan varias teorías de campos conformes con compactaciones de la teoría de cuerdas y la teoría M en varios números de dimensiones. Las teorías involucradas generalmente no son modelos viables del mundo real, pero tienen ciertas características, como su contenido de partículas o su alto grado de simetría, que las hacen útiles para resolver problemas en la teoría cuántica de campos y la gravedad cuántica.

El ejemplo más famoso de la correspondencia AdS/CFT afirma que la teoría de cuerdas tipo IIB en el espacio de producto AdS₅ × S⁵ es equivalente a N = 4 teoría supersimétrica de Yang-Mills en el límite de cuatro dimensiones. En este ejemplo, el espacio-tiempo en el que vive la teoría gravitacional es efectivamente de cinco dimensiones (de ahí la notación AdS₅), y hay cinco dimensiones compactas adicionales (codificadas por el S^{factor 5}). En el mundo real, el espacio-tiempo es de cuatro dimensiones, al menos macroscópicamente, por lo que esta versión de la correspondencia no proporciona un modelo realista de la gravedad. Asimismo, la teoría dual no es un modelo viable de ningún sistema del mundo real, ya que supone una gran cantidad de supersimetría. Sin embargo, como se explica más adelante, esta teoría de límites comparte algunas características en común con la cromodinámica cuántica, la teoría fundamental de la fuerza fuerte. Describe partículas similares a los gluones de la cromodinámica cuántica junto con ciertos fermiones. Como resultado, ha encontrado aplicaciones en la física nuclear, particularmente en el estudio del plasma de quarks-gluones.

Otro descubrimiento de la correspondencia afirma que la teoría M en AdS₇ × S⁴ es equivalente a la llamada teoría (2,0) en seis dimensiones. En este ejemplo, el espacio-tiempo de la teoría gravitacional es efectivamente de siete dimensiones. La existencia de la teoría (2,0) que aparece en un lado de la dualidad se predice mediante la clasificación de teorías de campos superconformes. Todavía no se comprende bien porque es una teoría de la mecánica cuántica sin límite clásico. A pesar de la dificultad inherente al estudio de esta teoría, se considera un objeto interesante por diversas razones, tanto físicas como matemáticas.

Otro descubrimiento más de la correspondencia afirma que la teoría M sobre AdS₄ × S⁷ es equivalente a la teoría de campos superconformales de ABJM en tres dimensiones. Aquí la teoría gravitacional tiene cuatro dimensiones no compactas, por lo que esta versión de la correspondencia proporciona una descripción algo más realista de la gravedad.

Aplicaciones a la gravedad cuántica

Una formulación no perturbativa de la teoría de cuerdas

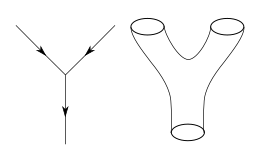
En la teoría cuántica de campos, normalmente se calculan las probabilidades de diversos eventos físicos utilizando las técnicas de la teoría de la perturbación. Desarrollada por Richard Feynman y otros en la primera mitad del siglo XX, la teoría cuántica de campos perturbativa utiliza diagramas especiales llamados diagramas de Feynman para organizar los cálculos. Uno imagina que estos diagramas representan las trayectorias de partículas puntuales y sus interacciones. Aunque este formalismo es extremadamente útil para hacer predicciones, estas predicciones sólo son posibles cuando la fuerza de las interacciones, la constante de acoplamiento, es lo suficientemente pequeña como para describir de manera confiable la teoría como cercana a una teoría sin interacciones.

El punto de partida de la teoría de cuerdas es la idea de que las partículas puntuales de la teoría cuántica de campos también pueden modelarse como objetos unidimensionales llamados cuerdas. La interacción de cuerdas se define más directamente generalizando la teoría de la perturbación utilizada en la teoría cuántica de campos ordinaria. En el nivel de los diagramas de Feynman, esto significa reemplazar el diagrama unidimensional que representa la trayectoria de una partícula puntual por una superficie bidimensional que representa el movimiento de una cuerda. A diferencia de la teoría cuántica de campos, la teoría de cuerdas aún no tiene una definición no perturbativa completa, por lo que muchas de las preguntas teóricas que a los físicos les gustaría responder siguen fuera de su alcance.

El problema de desarrollar una formulación no perturbativa de la teoría de cuerdas fue una de las motivaciones originales para estudiar la correspondencia AdS/CFT. Como se explicó anteriormente, la correspondencia proporciona varios ejemplos de teorías cuánticas de campos que son equivalentes a la teoría de cuerdas en el espacio anti-de Sitter. Alternativamente, se puede considerar que esta correspondencia proporciona una definición de la teoría de cuerdas en el caso especial en el que el campo gravitacional es asintóticamente anti-de Sitter (es decir, cuando el campo gravitacional se parece al del espacio anti-de Sitter). en el infinito espacial). Las cantidades físicamente interesantes en la teoría de cuerdas se definen en términos de cantidades en la teoría cuántica dual de campos.

Paradoja de la información del agujero negro

En 1975, Stephen Hawking publicó un cálculo que sugería que los agujeros negros no son completamente negros sino que emiten una radiación tenue debido a efectos cuánticos cerca del horizonte de sucesos. Al principio, el resultado de Hawking planteó un problema para los teóricos porque sugería que los agujeros negros destruyen información. Más precisamente, el cálculo de Hawking parecía entrar en conflicto con uno de los postulados básicos de la mecánica cuántica, que afirma que los sistemas físicos evolucionan en el tiempo según la ecuación de Schrödinger. Esta propiedad suele denominarse unitaridad de la evolución temporal. La aparente contradicción entre el cálculo de Hawking y el postulado de unitaridad de la mecánica cuántica llegó a ser conocida como la paradoja de la información del agujero negro.

La correspondencia AdS/CFT resuelve la paradoja de la información del agujero negro, al menos hasta cierto punto, porque muestra cómo un agujero negro puede evolucionar de una manera consistente con la mecánica cuántica en algunos contextos. De hecho, se pueden considerar los agujeros negros en el contexto de la correspondencia AdS/CFT, y cualquier agujero negro de este tipo corresponde a una configuración de partículas en el límite del espacio anti-de Sitter. Estas partículas obedecen a las reglas habituales de la mecánica cuántica y, en particular, evolucionan de forma unitaria, por lo que el agujero negro también debe evolucionar de forma unitaria, respetando los principios de la mecánica cuántica. En 2005, Hawking anunció que la correspondencia AdS/CFT había resuelto la paradoja a favor de la conservación de la información, y sugirió un mecanismo concreto mediante el cual los agujeros negros podrían preservar la información.

Aplicaciones a la teoría cuántica de campos

Física nuclear

Un sistema físico que se ha estudiado utilizando la correspondencia AdS/CFT es el plasma de quarks-gluones, un estado exótico de la materia producido en los aceleradores de partículas. Este estado de la materia surge durante breves instantes cuando iones pesados como los núcleos de oro o plomo chocan a altas energías. Tales colisiones hacen que los quarks que forman los núcleos atómicos se desconfinan a temperaturas de aproximadamente dos billones de grados Kelvin, condiciones similares a las presentes alrededor de 10⁻¹¹ segundos después del Big Bang.

La física del plasma de quarks-gluones se rige por la cromodinámica cuántica, pero esta teoría es matemáticamente intratable en problemas que involucran el plasma de quarks-gluones. En un artículo publicado en 2005, Đàm Thanh Sơn y sus colaboradores demostraron que la correspondencia AdS/CFT podría utilizarse para comprender algunos aspectos del plasma quark-gluón describiéndolo en el lenguaje de la teoría de cuerdas. Aplicando la correspondencia AdS/CFT, Sơn y sus colaboradores pudieron describir el plasma de quarks y gluones en términos de agujeros negros en el espacio-tiempo de cinco dimensiones. El cálculo mostró que la proporción de dos cantidades asociadas con el plasma de quarks y gluones, la viscosidad de corte η y la densidad volumétrica de entropía s, debería ser aproximadamente igual a un cierto valor universal. constante:

. . s. . ▪ ▪ 4π π k{displaystyle {frac {fnMicroc} }{s}approx {fnMic {hbar}{4pi k}}

donde ħ denota la constante de Planck reducida y k es la constante de Boltzmann. Además, los autores conjeturaron que esta constante universal proporciona un límite inferior para η/s en una gran clase de sistemas. En un experimento realizado en el Colisionador Relativista de Iones Pesados del Laboratorio Nacional de Brookhaven, el resultado experimental en un modelo estuvo cerca de este constante universal, pero no fue el caso en otro modelo.

Otra propiedad importante del plasma de quarks-gluones es que los quarks de muy alta energía que se mueven a través del plasma son detenidos o "apagados" después de recorrer sólo unos pocos femtómetros. Este fenómeno se caracteriza por un número ^q llamado parámetro de extinción del chorro, que relaciona la pérdida de energía de dicho quark con la distancia al cuadrado recorrida a través del plasma. Los cálculos basados en la correspondencia AdS/CFT dan el valor estimado ^q ≈ 4 GeV ²/fm y el valor experimental de ^ q se encuentra en el rango 5 –15 GeV²/fm.

Física de la materia condensada

A lo largo de décadas, los físicos experimentales de la materia condensada han descubierto una serie de estados exóticos de la materia, incluidos superconductores y superfluidos. Estos estados se describen utilizando el formalismo de la teoría cuántica de campos, pero algunos fenómenos son difíciles de explicar utilizando técnicas estándar de teoría de campos. Algunos teóricos de la materia condensada, incluido Subir Sachdev, esperan que la correspondencia AdS/CFT permita describir estos sistemas en el lenguaje de la teoría de cuerdas y aprender más sobre su comportamiento.

Hasta ahora se ha logrado cierto éxito en el uso de métodos de la teoría de cuerdas para describir la transición de un superfluido a un aislante. Un superfluido es un sistema de átomos eléctricamente neutros que fluye sin fricción. Estos sistemas suelen producirse en el laboratorio utilizando helio líquido, pero recientemente los experimentadores han desarrollado nuevas formas de producir superfluidos artificiales vertiendo billones de átomos fríos en una red de láseres entrecruzados. Estos átomos inicialmente se comportan como un superfluido, pero a medida que los experimentadores aumentan la intensidad de los láseres, se vuelven menos móviles y luego, repentinamente, pasan a un estado aislante. Durante la transición, los átomos se comportan de forma inusual. Por ejemplo, los átomos se detienen a un ritmo que depende de la temperatura y de la constante de Planck, parámetro fundamental de la mecánica cuántica, que no entra en la descripción de las otras fases. Este comportamiento se ha entendido recientemente considerando una descripción dual en la que las propiedades del fluido se describen en términos de un agujero negro de dimensiones superiores.

Crítica

Con muchos físicos recurriendo a métodos basados en cuerdas para resolver problemas en física nuclear y de materia condensada, algunos teóricos que trabajan en estas áreas han expresado dudas sobre si la correspondencia AdS/CFT puede proporcionar las herramientas necesarias para modelar de manera realista sistemas del mundo real. . En una charla en la conferencia Quark Matter en 2006, un físico estadounidense, Larry McLerran, señaló que la N = 4 teoría super Yang-Mills que aparece en la correspondencia AdS/CFT difiere significativamente de la cromodinámica cuántica, lo que dificulta la aplicación de estos métodos a la física nuclear. Según McLerran,

N = 4 supersymmetric Yang-Mills no es QCD... No tiene escala de masa y es conformativamente invariante. No tiene confinamiento ni constante de acoplamiento. Es supersimétrico. No tiene simetría quiral quebra o generación de masa. Tiene seis escalares y fermions en la representación conjunta... Puede ser posible corregir algunos o todos los problemas mencionados, o, para diversos problemas físicos, algunas de las objeciones pueden no ser pertinentes. Hasta ahora no hay consenso ni argumentos convincentes para las soluciones o fenómenos conjeturados que aseguran que N = 4 supersimétrica Los resultados de Yang Mills reflejarían de forma fiable el QCD.

En una carta a Physics Today, el premio Nobel Philip W. Anderson expresó preocupaciones similares sobre las aplicaciones de AdS/CFT a la física de la materia condensada, afirmando

Como un problema muy general con el enfoque AdS/CFT en la teoría de la materia condensada, podemos apuntar a esas iniciales de narración "CFT" — teoría de campo conformada. Los problemas de materia condensada no son, en general, ni relativistas ni conformales. Cerca de un punto crítico cuántico, el tiempo y el espacio pueden estar escalando, pero incluso allí todavía tenemos un sistema de coordenadas preferido y, por lo general, una celosía. Hay algunas evidencias de otras fases lineales-T a la izquierda del extraño metal sobre el cual son bienvenidos a especular, pero de nuevo en este caso el problema de la materia condensada está sobredeterminado por hechos experimentales.

Historia y desarrollo

Teoría de cuerdas y física nuclear

El descubrimiento de la correspondencia AdS/CFT a finales de 1997 fue la culminación de una larga historia de esfuerzos para relacionar la teoría de cuerdas con la física nuclear. De hecho, la teoría de cuerdas se desarrolló originalmente a finales de los años 1960 y principios de los 1970 como una teoría de los hadrones, las partículas subatómicas como el protón y el neutrón que se mantienen unidas por la fuerza nuclear fuerte. La idea era que cada una de estas partículas pudiera verse como un modo de oscilación diferente de una cuerda. A finales de la década de 1960, los experimentadores descubrieron que los hadrones se dividen en familias llamadas trayectorias de Regge con energía al cuadrado proporcional al momento angular, y los teóricos demostraron que esta relación surge naturalmente de la física de una cuerda relativista en rotación.

Por otro lado, los intentos de modelar hadrones como cuerdas enfrentaron serios problemas. Un problema fue que la teoría de cuerdas incluye una partícula de espín-2 sin masa, mientras que tal partícula no aparece en la física de los hadrones. Una partícula así mediaría una fuerza con las propiedades de la gravedad. En 1974, Joël Scherk y John Schwarz sugirieron que la teoría de cuerdas no era, por tanto, una teoría de la física nuclear como habían pensado muchos teóricos, sino una teoría de la gravedad cuántica. Al mismo tiempo, se descubrió que los hadrones en realidad están hechos de quarks y se abandonó el enfoque de la teoría de cuerdas en favor de la cromodinámica cuántica.

En cromodinámica cuántica, los quarks tienen un tipo de carga que se presenta en tres variedades llamadas colores. En un artículo de 1974, Gerard 't Hooft estudió la relación entre la teoría de cuerdas y la física nuclear desde otro punto de vista, considerando teorías similares a la cromodinámica cuántica, donde el número de colores es un número arbitrario N, en lugar de tres. En este artículo, 't Hooft consideró un cierto límite donde N tiende al infinito y argumentó que en este límite ciertos cálculos en la teoría cuántica de campos se parecen a los cálculos en la teoría de cuerdas.

Agujeros negros y holografía

En 1975, Stephen Hawking publicó un cálculo que sugería que los agujeros negros no son completamente negros sino que emiten una radiación tenue debido a efectos cuánticos cerca del horizonte de sucesos. Este trabajo amplió los resultados anteriores de Jacob Bekenstein, quien había sugerido que los agujeros negros tienen una entropía bien definida. Al principio, el resultado de Hawking parecía contradecir uno de los principales postulados de la mecánica cuántica, a saber, la unitaridad de la evolución del tiempo. Intuitivamente, el postulado de la unitaridad dice que los sistemas de la mecánica cuántica no destruyen la información a medida que evolucionan de un estado a otro. Por esta razón, la aparente contradicción pasó a conocerse como la paradoja de la información del agujero negro.

Más tarde, en 1993, Gerard 't Hooft escribió un artículo especulativo sobre la gravedad cuántica en el que revisó el trabajo de Hawking sobre la termodinámica de los agujeros negros y concluyó que el número total de grados de libertad en una región de El espacio-tiempo que rodea un agujero negro es proporcional a la superficie del horizonte. Esta idea fue promovida por Leonard Susskind y ahora se conoce como principio holográfico. El principio holográfico y su realización en la teoría de cuerdas a través de la correspondencia AdS/CFT han ayudado a dilucidar los misterios de los agujeros negros sugeridos por el trabajo de Hawking y se cree que proporcionan una resolución de la paradoja de la información de los agujeros negros. En 2004, Hawking admitió que los agujeros negros no violan la mecánica cuántica y sugirió un mecanismo concreto mediante el cual podrían preservar información.

Papel de Maldacena

El 1 de enero de 1998, Juan Maldacena publicó un artículo histórico que inició el estudio de AdS/CFT. Según Alexander Markovich Polyakov, "el trabajo de [Maldacena] abrió las compuertas". La conjetura despertó inmediatamente un gran interés en la comunidad de la teoría de cuerdas y fue considerada en un artículo de Steven Gubser, Igor Klebanov y Polyakov, y en otro artículo de Edward Witten. Estos artículos hicieron más precisa la conjetura de Maldacena y mostraron que la teoría de campo conforme que aparece en la correspondencia vive en el límite del espacio anti-de Sitter.

Un caso especial de la propuesta de Maldacena dice que N = 4 teoría súper Yang-Mills, una teoría de calibre similar en algunos aspectos Según la cromodinámica cuántica, es equivalente a la teoría de cuerdas en el espacio anti-De Sitter de cinco dimensiones. Este resultado ayudó a aclarar el trabajo anterior de 't Hooft sobre la relación entre la teoría de cuerdas y la cromodinámica cuántica, llevando la teoría de cuerdas a sus raíces como teoría de la física nuclear. Los resultados de Maldacena también proporcionaron una realización concreta del principio holográfico con importantes implicaciones para la gravedad cuántica y la física de los agujeros negros. Para el año 2015, el artículo de Maldacena se había convertido en el artículo más citado en física de altas energías con más de 10.000 citas. Estos artículos posteriores han proporcionado pruebas considerables de que la correspondencia es correcta, aunque hasta ahora no se ha demostrado rigurosamente.

Generalizaciones

Gravedad tridimensional

Para comprender mejor los aspectos cuánticos de la gravedad en nuestro universo de cuatro dimensiones, algunos físicos han considerado un modelo matemático de dimensiones inferiores en el que el espacio-tiempo tiene sólo dos dimensiones espaciales y una dimensión temporal. En este contexto, las matemáticas que describen el campo gravitacional se simplifican drásticamente y se puede estudiar la gravedad cuántica utilizando métodos familiares de la teoría cuántica de campos, eliminando la necesidad de la teoría de cuerdas u otros enfoques más radicales de la gravedad cuántica en cuatro dimensiones.

A partir del trabajo de J. David Brown y Marc Henneaux en 1986, los físicos han notado que la gravedad cuántica en un espacio-tiempo tridimensional está estrechamente relacionada con la teoría de campos conforme bidimensional. En 1995, Henneaux y sus colaboradores exploraron esta relación con más detalle, sugiriendo que la gravedad tridimensional en el espacio anti-de Sitter es equivalente a la teoría de campos conforme conocida como teoría de campos de Liouville. Otra conjetura formulada por Edward Witten afirma que la gravedad tridimensional en el espacio anti-de Sitter es equivalente a una teoría de campos conforme con simetría de grupo de monstruos. Estas conjeturas proporcionan ejemplos de la correspondencia AdS/CFT que no requieren el aparato completo de la teoría de cuerdas o M.

Correspondencia DS/CFT

A diferencia de nuestro universo, que ahora se sabe que se está expandiendo a un ritmo acelerado, el espacio anti-de Sitter no se expande ni se contrae. En cambio, luce igual en todo momento. En un lenguaje más técnico, se dice que el espacio anti-de Sitter corresponde a un universo con una constante cosmológica negativa, mientras que el universo real tiene una pequeña constante cosmológica positiva.

Aunque las propiedades de la gravedad a distancias cortas deberían ser algo independientes del valor de la constante cosmológica, es deseable tener una versión de la correspondencia AdS/CFT para la constante cosmológica positiva. En 2001, Andrew Strominger introdujo una versión de la dualidad llamada correspondencia dS/CFT. Esta dualidad involucra un modelo de espacio-tiempo llamado espacio de Sitter con una constante cosmológica positiva. Esta dualidad es interesante desde el punto de vista de la cosmología, ya que muchos cosmólogos creen que el universo primitivo estaba cerca de ser el espacio de De Sitter.

Correspondencia Kerr/CFT

Aunque la correspondencia AdS/CFT suele ser útil para estudiar las propiedades de los agujeros negros, la mayoría de los agujeros negros considerados en el contexto de AdS/CFT son físicamente poco realistas. De hecho, como se explicó anteriormente, la mayoría de las versiones de la correspondencia AdS/CFT involucran modelos de espacio-tiempo de dimensiones superiores con supersimetría no física.

En 2009, Monica Guica, Thomas Hartman, Wei Song y Andrew Strominger demostraron que, no obstante, las ideas de AdS/CFT podían utilizarse para comprender ciertos agujeros negros astrofísicos. Más precisamente, sus resultados se aplican a los agujeros negros que se aproximan a los agujeros negros extremos de Kerr, que tienen el mayor momento angular posible compatible con una masa determinada. Demostraron que tales agujeros negros tienen una descripción equivalente en términos de teoría de campos conforme. La correspondencia Kerr/CFT se extendió posteriormente a los agujeros negros con menor momento angular.

Teorías del indicador de giro superior

La correspondencia AdS/CFT está estrechamente relacionada con otra dualidad conjeturada por Igor Klebanov y Alexander Markovich Polyakov en 2002. Esta dualidad establece que ciertas "teorías de calibre de espín superior" en el espacio anti-de Sitter son equivalentes a teorías de campos conformes con simetría O (N). Aquí la teoría en su conjunto es un tipo de teoría de calibre que describe partículas de espín arbitrariamente alto. Es similar a la teoría de cuerdas, donde los modos excitados de las cuerdas vibrantes corresponden a partículas con mayor espín, y puede ayudar a comprender mejor las versiones teóricas de cuerdas de AdS/CFT y posiblemente incluso probar la correspondencia. En 2010, Simone Giombi y Xi Yin obtuvieron más pruebas de esta dualidad calculando cantidades llamadas funciones de tres puntos.