Copo de nieve de Koch

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

El Copo de Nieve de Koch es un tipo de curva fractal en el que el perímetro crece infinitamente mientras su área solo crece de forma finita, con cada iteración. El crecimiento total del área cuando las iteraciones tienden a infinito es de 8/5 (1.6 en decimal). El Copo de Koch fue uno de los primeros en ser descubiertos y se originó gracias al trabajo del matemático sueco Helge von Koch, y ha recibido múltiples nombres, todos aceptables, tales como: Curva de Koch o Fractal de Koch, cuando se hace referencia a su progresión, o Estrella de Koch e Isla de Koch, cuando se hace referencia a su forma geométrica.

Para construir un Copo de Nieve de Koch se requiere un proceso iterativo (etapas sucesivas) que inicia de forma sencilla: un triángulo equilátero. En cada etapa sucesiva, se añade un triángulo equilátero más pequeño, en el centro cada lado de la figura, con una longitud de una 1/3 de la longitud del lado. Con lo que progresivamente, va adquiriendo su forma característica de un copo de nieve.

Una característica notable del Copo de Nieve de Koch es la convergencia de su área y la expansión de su perímetro. A medida que se avanza en las etapas de construcción, las áreas encerradas por estas convergen hacia el infinito en un valor que es 8/5 veces mayor que el área del triángulo original. Mientras por otro lado, el perímetro del copo de nieve sigue aumentando infinitamente. Este fenómeno resulta en una figura que, aunque encierra una zona finita, posee un perímetro infinito.

La Curva del Copo de Koch, fue descrita por primera vez en su artículo de 1904, "Sobre una curva continua sin tangentes, construible a partir de la geometría elemental". Desde ese momento es un ejemplo clásico de cómo un proceso iterativo simple puede generar un patrón altamente complejo y detallado, y se usa a menudo en matemáticas y ciencias de la computación para ilustrar los conceptos de auto-similitud y fractales.

HSD

Construcción

Imágen que muestra la progresión del incremento en el área del Copo de Koch

El copo de nieve de Koch se puede construir comenzando con un triángulo equilátero y luego modificando recursivamente cada segmento de línea de la siguiente manera:

dividir el segmento de línea en tres segmentos de igual longitud.
dibujar un triángulo equilátero que tiene el segmento medio del paso 1 como su base y apunta hacia fuera.
eliminar el segmento de línea que es la base del triángulo del paso 2.

La primera iteración de este proceso produce el contorno de un hexagrama.

El copo de nieve de Koch es el límite al que se acerca a medida que se siguen los pasos anteriores indefinidamente. La curva de Koch descrita originalmente por Helge von Koch se construye usando solo uno de los tres lados del triángulo original. En otras palabras, tres curvas de Koch forman un copo de nieve de Koch.

Se puede crear una representación basada en la curva de Koch de una superficie nominalmente plana segmentando repetidamente cada línea en un patrón de dientes de sierra de segmentos con un ángulo determinado.

Una superficie rugosa fractal construida a partir de múltiples iteraciones de curva Koch

Propiedades

Perímetro del copo de nieve de Koch

Cada iteración multiplica el número de lados en el copo de nieve Koch por cuatro, por lo que el número de lados después de $n$ iteraciones se da por:

{displaystyle N_{n}=N_{n-1}cdot 4=3cdot 4^{n},.}

Si el triángulo equilátero original tiene lados de longitud $s$ , la longitud de cada lado del copo de nieve después $n$ iteraciones es:

{displaystyle S_{n}={frac {S_{n-1}}{3}}={frac {s}{3^{n}}},,}

un poder inverso de tres múltiples de la longitud original.
El perímetro del copo de nieve después $n$ iteraciones es:

{displaystyle P_{n}=N_{n}cdot S_{n}=3cdot scdot {left({frac {4}{3}}right)}^{n},.}

La curva Koch tiene una longitud infinita, porque la longitud total de la curva aumenta por un factor de $tfrac{4}{3}$ con cada iteración. Cada iteración crea cuatro veces más segmentos de línea como en la iteración anterior, con la longitud de cada ser ${tfrac {1}{3}}$ la longitud de los segmentos en la etapa anterior. Por lo tanto, la longitud de la curva después $n$ iteraciones serán ${displaystyle ({tfrac {4}{3}})^{n}}$ veces el perímetro del triángulo original y es sin límites, como $n$ tiende a la infinidad.

Límite del perímetro

Zoom infinito sobre la progresión de la Curva de Koch

Como el número de iteraciones tiende a infinito, el límite del perímetro es:

{displaystyle lim _{nrightarrow infty }P_{n}=lim _{nrightarrow infty }3cdot scdot left({frac {4}{3}}right)^{n}=infty ,,}

desde entonces $1}" xmlns="http://www.w3.org/1998/Math/MathML">43■1{fnMicroc} {4}{3}}}]1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8d2e3325ea0fcaa36d9df404c2a283c85bb151c8" style="vertical-align: -1.338ex; width:5.919ex; height:3.676ex;"/>$ .

An ${displaystyle {tfrac {ln 4}{ln 3}}}$ - la medida dimensional existe, pero no se ha calculado hasta ahora. Sólo se han inventado límites superiores e inferiores.

Área del copo de nieve de Koch

En cada iteración se añade un nuevo triángulo en cada lado de la iteración anterior, por lo que el número de nuevos triángulos añadidos en la iteración $n$ es:

{displaystyle T_{n}=N_{n-1}=3cdot 4^{n-1}={frac {3}{4}}cdot 4^{n},.}

El área de cada nuevo triángulo añadido en una iteración es ${displaystyle {tfrac {1}{9}}}$ del área de cada triángulo añadido en la iteración anterior, por lo que el área de cada triángulo añadido en iteración $n$ es:

{displaystyle a_{n}={frac {a_{n-1}}{9}}={frac {a_{0}}{9^{n}}},.}

Donde $a_{0}$ es el área del triángulo original. El nuevo área total añadido en iteración $n$ es, pues,:

{displaystyle b_{n}=T_{n}cdot a_{n}={frac {3}{4}}cdot {left({frac {4}{9}}right)}^{n}cdot a_{0}}

El área total del copo de nieve después $n$ iteraciones es:

{displaystyle A_{n}=a_{0}+sum _{k=1}^{n}b_{k}=a_{0}left(1+{frac {3}{4}}sum _{k=1}^{n}left({frac {4}{9}}right)^{k}right)=a_{0}left(1+{frac {1}{3}}sum _{k=0}^{n-1}left({frac {4}{9}}right)^{k}right),.}

Comprimir la suma geométrica da:

{displaystyle A_{n}=a_{0}left(1+{frac {3}{5}}left(1-left({frac {4}{9}}right)^{n}right)right)={frac {a_{0}}{5}}left(8-3left({frac {4}{9}}right)^{n}right),.}

Límites del área

El límite del área es:

{displaystyle lim _{nrightarrow infty }A_{n}=lim _{nrightarrow infty }{frac {a_{0}}{5}}cdot left(8-3left({frac {4}{9}}right)^{n}right)={frac {8}{5}}cdot a_{0},,}

desde entonces $<math alttext="{displaystyle {tfrac {4}{9}}49.1{fnMicroc} {4}{9} {1}<img alt="{displaystyle {tfrac {4}{9}}$ .

Así, la zona del copo de nieve Koch es ${displaystyle {tfrac {8}{5}}}$ del área del triángulo original. Expresado en términos de la longitud lateral $s$ del triángulo original, esto es:

{displaystyle {frac {2s^{2}{sqrt {3}}}{5}}.}

Sólida de la revolución

(feminine)

El volumen del sólido de la revolución del copo de nieve de Koch sobre un eje de simetría del triángulo equilátero iniciado del lado unitario es ${displaystyle {frac {11{sqrt {3}}}{135}}pi.}$

Otras propiedades

El copo de nieve de Koch se autorreplica con seis copias más pequeñas que rodean una copia más grande en el centro. Por lo tanto, es un irrep-7 irrep-tile (ver Rep-tile para la discusión).

La dimensión fractal de la curva Koch es ${displaystyle {tfrac {ln 4}{ln 3}}approx 1.26186}$ . Esto es mayor que el de una línea ( $=1$ ) pero menos que la curva de relleno espacial de Peano ( ${displaystyle =2}$ ).

La curva de Koch es continua en todas partes, pero diferenciable en ninguna.

Teselación del plano

Tessellation por dos tamaños de copo de nieve Koch

Es posible teselar el plano con copias de los copos de nieve de Koch en dos tamaños diferentes. Sin embargo, dicha teselación no es posible usando solo copos de nieve de un tamaño. Dado que cada copo de nieve de Koch en el mosaico se puede subdividir en siete copos de nieve más pequeños de dos tamaños diferentes, también es posible encontrar mosaicos que usen más de dos tamaños a la vez. Se pueden usar copos de nieve de Koch y anti-copos de nieve de Koch del mismo tamaño para embaldosar el avión.

Secuencia Thue-Morse y gráficos de tortuga

Un gráfico de tortuga es la curva que se genera si se programa un autómata con una secuencia.
Si se utilizan los miembros de la secuencia Thue-Morse para seleccionar los estados del programa:

Si ${displaystyle t(n)=0}$ , adelante por una unidad,
Si ${displaystyle t(n)=1}$ , girar en sentido contrario por un ángulo ${tfrac {pi }{3}}$ ,

la curva resultante converge al copo de nieve de Koch.

Representación como sistema Lindenmayer

La curva de Koch se puede expresar mediante el siguiente sistema de reescritura (sistema de Lindenmayer):

Alfabeto: F

Constantes: +, −

Axiom: F

Normas de producción:

F → F+F--F+F

Aquí, F significa "avanzar", - significa "girar a la derecha 60°" y + significa "girar a la izquierda 60°".

Para crear el copo de nieve de Koch, se usaría F--F--F (un triángulo equilátero) como axioma.

Variantes de la curva de Koch

Siguiendo el concepto de von Koch, se diseñaron varias variantes de la curva de Koch, considerando ángulos rectos (cuadráticos), otros ángulos (Cesàro), círculos y poliedros y sus extensiones a dimensiones superiores (Sphereflake y Kochcube, respectivamente)

Variante (dimensión, ángulo)	Ilustración	Construcción
≤1D, ángulo de 60-90°	Cesàro fractal (85°)	El Cesàro fractal es una variante de la curva Koch con un ángulo entre 60° y 90°. $Cesàro fractal outlines 1-4.svg$ Primero cuatro iteraciones de un antisnowflake Cesàro (cuatro curvas de 60° dispuestas en un cuadrado de 90°)
■1.46D, ángulo de 90°	Curva del tipo 1	Primero dos iteraciones
1,5D, ángulo de 90°	Curva cuadrática tipo 2	Salchichas de Minkowski Primero dos iteraciones. Su dimensión fractal es igual ${displaystyle {tfrac {3}{2}}}$ y es exactamente medio camino entre la dimensión 1 y 2. Por lo tanto, a menudo se elige cuando se estudian las propiedades físicas de objetos fractales no enteros.
≤2D, ángulo de 90°	Tercera iteración	Minkowski Island Cuatro curvas cuadradas tipo 2 dispuestas en un cuadrado
■1.37D, ángulo de 90°	Flake Quadratic	4 curvas de tipo cuadrático 1 dispuestas en un polígono: Primero dos iteraciones. Conocida como la "Salsa de Minkowski", su dimensión fractal equivale a ${displaystyle {tfrac {ln 3}{ln {sqrt {5}}}}=1.36521}$ .
≤2D, ángulo de 90°	Antiflake Quadratic	Anticurva de punta cruzada, el tipo de flake cuadrático 1, con las curvas hacia adentro en lugar de hacia fuera (Vicsek fractal)
Ω1.49D, ángulo de 90°	Quadratic Cross	Otra variación. Su dimensión fractal es igual ${displaystyle {frac {ln 3.33}{ln {sqrt {5}}}}=1.49}$ .
≤2D, ángulo de 90°	Isla Cuadrática	Curva cuadrática, iteraciones 0, 1, y 2; dimensión de ${displaystyle {tfrac {ln 18}{ln 6}}approx 1.61}$
≤2D, ángulo de 60°	Superficie de von Koch	Primero tres iteraciones de una extensión natural de la curva Koch en dos dimensiones.
≤2D, ángulo de 90°	$Koch quadratic 3d fractal.svg$ Primero (bloque azul), segundo (más bloques verdes), tercero (más bloques amarillos) y cuarto (más bloques transparentes) iteraciones del tipo 1 3D Koch quadratic fractal	Ampliación de la curva tipo 1 cuadrática. La ilustración a la izquierda muestra el fractal después de la segunda iteración Superficie cuadrática de animación
≤3D, cualquier	$Koch Curve in Three Dimensions ("Delta" fractal).jpg$ Curva de Koch en 3D	Un fractal tridimensional construido a partir de curvas Koch. La forma se puede considerar una extensión tridimensional de la curva en el mismo sentido que la pirámide Sierpiński y la esponja Menger pueden considerarse extensiones del triángulo Sierpinski y alfombra Sierpinski. La versión de la curva utilizada para esta forma utiliza ángulos de 85°.

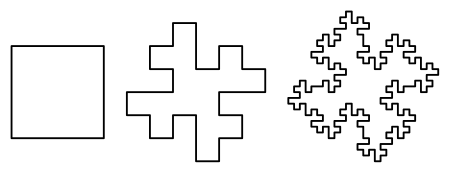
Las plazas se pueden utilizar para generar curvas fractales similares. Comenzando con un cuadrado de unidad y añadiendo a cada lado en cada iteración un cuadrado con dimensión un tercio de los cuadrados en la iteración anterior, se puede demostrar que tanto la longitud del perímetro como el área total se determinan por progresiones geométricas. La progresión para la zona converge a $2$ Mientras la progresión para el perímetro se divierte en infinito, así como en el caso del copo de nieve Koch, tenemos un área finita ligada por una curva fractal infinita. El área resultante llena un cuadrado con el mismo centro que el original, pero dos veces el área, y girado por $tfrac{pi}{4}$ radians, el perímetro tocando pero nunca superando.

El área total cubierta por $n$ la iteración es:

{displaystyle A_{n}={frac {1}{5}}+{frac {4}{5}}sum _{k=0}^{n}left({frac {5}{9}}right)^{k}quad {mbox{giving}}quad lim _{nrightarrow infty }A_{n}=2,,}

mientras que la longitud total del perímetro es:

{displaystyle P_{n}=4left({frac {5}{3}}right)^{n}a,,}

$n$

Galería

Sexta iteración de la Curva de Koch cuando se construye removiendo fragmentos — Sexta iteración de la Curva de Koch removiendo fragmentos

Contenido relacionado

Más resultados...