Constante de Ramanujan-Soldner

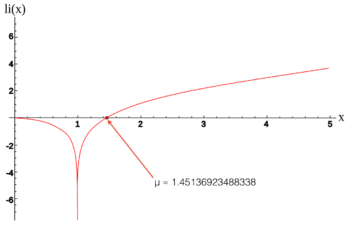
En matemáticas, la constante de Ramanujan-Soldner (también llamada constante de Soldner) es una constante matemática definida como el único cero positivo de la función integral logarítmica. Lleva el nombre de Srinivasa Ramanujan y Johann Georg von Soldner.

Su valor es aproximadamente μ ≈ 1.45136923488338105028396848589202744949303228… (secuencia A070769 en el OEIS)

Dado que la integral logarítmica está definida por

li()x)=∫ ∫ 0xdtIn⁡ ⁡ t,{displaystyle mathrm {li} (x)=int _{0}{x}{frac {dt}{ln t}}}

luego usar li()μ μ )=0,{displaystyle mathrm {li} (mu)=0,} tenemos

li()x)=li()x)− − li()μ μ )=∫ ∫ 0xdtIn⁡ ⁡ t− − ∫ ∫ 0μ μ dtIn⁡ ⁡ t=∫ ∫ μ μ xdtIn⁡ ⁡ t,{displaystyle mathrm {li} (x);=;mathrm {li} (x)-mathrm {li} (mu)=int _{0}{x}{frac {dt}{ln} {ln} t}- ¿Qué? }{frac {dt}{ln ¿Qué?

this easing calculation for numbers greater than μ. Also, since the exponential integral function satisfies the equation

li()x)=Ei()In⁡ ⁡ x),{displaystyle mathrm {li} (x);=;mathrm {Ei} (ln {x}),}

el único cero positivo de la integral exponencial se produce en el logaritmo natural de la constante de Ramanujan-Soldner, cuyo valor es aproximadamente ln(μ) ≈ 0,372507410781366634461991866… (secuencia A091723 en la OEIS)