Constante de acoplamiento

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Parámetro que describe la fuerza de una fuerza

En física, una acoplamiento constante o parámetro de acoplamiento de calibre (o, más simplemente, un acoplamiento), es un número que determina la fuerza de la fuerza ejercida en una interacción. Originalmente, la constante de acoplamiento relacionaba la fuerza actuando entre dos cuerpos estáticos a las "cargas" de los cuerpos (es decir, la carga eléctrica para la electrostática y la masa para la gravedad Newtoniana) dividida por la distancia cuadrada, ${displaystyle r^{2}}$ , entre los cuerpos; así: ${displaystyle G}$ dentro ${displaystyle F=Gm_{1}m_{2}/r^{2}}$ para la gravedad newtoniana y ${displaystyle k_{text{e}}}$ dentro ${displaystyle F=k_{text{e}}q_{1}q_{2}/r^{2}}$ para electrostático. Esta descripción sigue siendo válida en física moderna para teorías lineales con cuerpos estáticos y portadores de fuerza sin masa.

Una definición moderna y más general utiliza el Lagrangian ${displaystyle {mathcal {L}}}$ (o equivalente al Hamiltonian ${displaystyle {mathcal {H}}}$ ) de un sistema. Por lo general, ${displaystyle {mathcal {L}}}$ (o ${displaystyle {mathcal {H}}}$ ) de un sistema que describa una interacción se puede separar en un Parte cinética ${displaystyle T}$ y un parte de la interacción ${displaystyle V}$ : ${displaystyle {mathcal {L}}=T-V}$ (o ${displaystyle {mathcal {H}}=T+V}$ ). En teoría de campo, ${displaystyle V}$ Siempre contiene 3 términos o más campos, expresando por ejemplo que un electron inicial (campo 1) interactuó con un fotón (campo 2) produciendo el estado final del electrón (campo 3). En contraste, el Parte cinética ${displaystyle T}$ siempre contiene sólo dos campos, expresando la libre propagación de una partícula inicial (campo 1) en un estado posterior (campo 2). La constante de acoplamiento determina la magnitud de la ${displaystyle T}$ con respecto a la ${displaystyle V}$ parte (o entre dos sectores de la parte de interacción si hay varios campos que están diferentes). Por ejemplo, la carga eléctrica de una partícula es una constante de acoplamiento que caracteriza una interacción con dos campos de carga y un campo de fotones (de ahí el diagrama común Feynman con dos flechas y una línea ondulada). Dado que los fotones median la fuerza electromagnética, este acoplamiento determina lo fuerte que los electrones sienten tal fuerza, y tiene su valor fijado por experimento. Al mirar el QED Lagrangian, se ve que de hecho, el acoplamiento establece la proporcionalidad entre el término cinético ${displaystyle T={bar {psi }}(ihbar cgamma ^{sigma }partial _{sigma }-mc^{2})psi -{1 over 4mu _{0}}F_{mu nu }F^{mu nu }}$ y el término de interacción ${displaystyle V=-e{bar {psi }}(hbar cgamma ^{sigma }A_{sigma })psi }$ .

Un acoplamiento juega un papel importante en la dinámica. Por ejemplo, a menudo se establecen jerarquías de aproximación basadas en la importancia de varias constantes de acoplamiento. En el movimiento de un gran bulto de hierro magnetizado, las fuerzas magnéticas pueden ser más importantes que las fuerzas gravitatorias debido a las magnitudes relativas de las constantes de acoplamiento. Sin embargo, en la mecánica clásica, uno suele tomar estas decisiones directamente comparando fuerzas. Otro ejemplo importante del papel central desempeñado por las constantes de acoplamiento es que son los parámetros de expansión para los cálculos de primer principio basados en la teoría de la perturbación, que es el principal método de cálculo en muchas ramas de la física.

Constante de estructura fina

Los acoplamientos surgen naturalmente en una teoría cuántica de campos. En las teorías cuánticas relativistas los acoplamientos adimensionales desempeñan un papel especial; es decir, son números puros. Un ejemplo de una constante adimensional es la constante de estructura fina,

{displaystyle alpha ={frac {e^{2}}{4pi varepsilon _{0}hbar c}},}

donde $e$ es la carga de un electrón, $ε 0$ es la permitividad del espacio libre, $ħ$ es la constante de Planck reducida y $c$ es la velocidad de la luz. Esta constante es proporcional al cuadrado de la fuerza de acoplamiento de la carga de un electrón al campo electromagnético.

Acoplamiento de calibre

En una teoría del calibre no abeliano, la parámetro de acoplamiento de calibre, ${displaystyle g}$ , aparece en el Lagrangiano como

{displaystyle {frac {1}{4g^{2}}}{rm {Tr}},G_{mu nu }G^{mu nu },}

(donde) G es el tensor de campo medidor) en algunas convenciones. En otra convención ampliamente utilizada, G se reescala para que el coeficiente del término cinético sea 1/4 y ${displaystyle g}$ aparece en el derivado covariante. Esto debe entenderse como una versión sin dimensiones de la carga elemental definida como

{displaystyle {frac {e}{sqrt {varepsilon _{0}hbar c}}}={sqrt {4pi alpha }}approx 0.30282212 ~~.}

Acoplamiento débil y fuerte

En una teoría de campo cuántica con un acoplamiento g, si g es mucho menos de 1, la teoría se dice que débilmente acoplado. En este caso, está bien descrito por una expansión de poderes g, llamada teoría de la perturbación. Si la constante de acoplamiento es de orden uno o más, se dice que la teoría es fuertemente unidos. Un ejemplo de este último es la teoría hadrónica de fuertes interacciones (por eso se llama fuerte en primer lugar). En tal caso, es necesario utilizar métodos no permanentes para investigar la teoría.

En la teoría de campo cuántica, la dimensión del acoplamiento juega un papel importante en la propiedad de la teoría de la renormalización, y por lo tanto en la aplicabilidad de la teoría de la perturbación. Si el acoplamiento no tiene dimensión en el sistema de unidades naturales (es decir, ${displaystyle c=1}$ , ${displaystyle hbar =1}$ ), como en QED, QCD y la interacción débil, la teoría es renormalizable y todos los términos de la serie de expansión son finitos (después de la renormalización). Si el acoplamiento es dimensional, como por ejemplo en gravedad ( ${displaystyle [G_{N}]={text{energy}}^{-2}}$ ), la teoría de Fermi ${displaystyle [G_{F}]={text{energy}}^{-2}}$ ) o la teoría de perturbación chiral de la fuerza fuerte ( ${displaystyle [F]={text{energy}}}$ ), entonces la teoría generalmente no es renormalizable. Las expansiones de perturbación en el acoplamiento todavía pueden ser factibles, aunque dentro de las limitaciones, ya que la mayoría de los términos de orden superior de la serie será infinita.

Acoplamiento

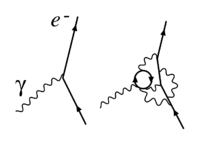
Uno puede sondear una teoría de campo cuántica en tiempos cortos o distancias cambiando la longitud de onda o el impulso, kDe la sonda utilizada. Con una sonda de alta frecuencia (es decir, tiempo corto) se ve que las partículas virtuales participan en cada proceso. Esta aparente violación de la conservación de la energía puede entenderse heurísticamente examinando la relación de incertidumbre

{displaystyle Delta EDelta tgeq {frac {hbar }{2}},}

que permite virtualmente tales violaciones a corto plazo. La observación anterior sólo se aplica a algunas formulaciones de la teoría del campo cuántico, en particular la cuantificación canónica en el cuadro de interacción.

En otras formulaciones, el mismo evento se describe mediante eventos "virtual" partículas que salen de la capa de masa. Tales procesos renormalizan el acoplamiento y lo hacen dependiente de la escala de energía, μ, en la que se analiza el acoplamiento. La dependencia de un acoplamiento g(μ) de la escala de energía se conoce como "funcionamiento del acoplamiento". La teoría del funcionamiento de los acoplamientos viene dada por el grupo de renormalización, aunque se debe tener en cuenta que el grupo de renormalización es un concepto más general que describe cualquier tipo de variación de escala en un sistema físico (consulte el artículo completo para obtener más detalles).

Fenomenología del funcionamiento de un acoplamiento

El grupo de renormalización proporciona una forma formal de derivar el funcionamiento de un acoplamiento, pero la fenomenología subyacente que se ejecuta puede entenderse intuitivamente. Como se explica en la introducción, el acoplamiento constante establece la magnitud de una fuerza que se comporta con la distancia como ${displaystyle 1/r^{2}}$ . El ${displaystyle 1/r^{2}}$ - La dependencia fue explicada por primera vez por Faraday como la disminución del flujo de fuerza: en un momento B distante ${displaystyle r}$ del cuerpo A generando una fuerza, ésta es proporcional al flujo de campo que atraviesa una superficie elemental S perpendicular a la línea AB. A medida que el flujo se extiende uniformemente a través del espacio, disminuye según el ángulo sólido que sostiene la superficie S. En la visión moderna de la teoría del campo cuántico, la ${displaystyle 1/r^{2}}$ proviene de la expresión en espacio de posición del propagador de los portadores de fuerza. Para los cuerpos de interacción relativamente débil, como es generalmente el caso en el electromagnetismo o la gravedad o las interacciones nucleares a corta distancia, el intercambio de un solo portador de fuerza es una buena primera aproximación de la interacción entre los cuerpos, y clásicamente la interacción obedecerá a una ${displaystyle 1/r^{2}}$ -Ley (nota que si el portador de fuerza es masivo, hay adicional ${displaystyle r}$ dependencia). Cuando las interacciones son más intensas (por ejemplo, los cargos o las masas son mayores, o ${displaystyle r}$ es más pequeño) o ocurre con períodos de tiempo más breves (smaller ${displaystyle r}$ ), más portadores de fuerza están involucrados o se crean pares de partículas, véase Fig. 1, que resulta en la desintegración de la ${displaystyle 1/r^{2}}$ comportamiento. El equivalente clásico es que el flujo de campo no se propaga libremente en el espacio más pero por ejemplo se somete a la detección de los cargos de las partículas virtuales adicionales, o interacciones entre estas partículas virtuales. Es conveniente separar el primer orden ${displaystyle 1/r^{2}}$ ley de este extra ${displaystyle r}$ - La dependencia. Este último se explica por ser incluido en el acoplamiento, que luego se convierte en ${displaystyle 1/r}$ -dependiente, (o equivalente μ-dependiente). Dado que las partículas adicionales involucradas más allá de la aproximación de un solo transportista de fuerza son siempre virtuales, es decir, fluctuaciones de campo cuántico transitorio, se entiende por qué el funcionamiento de un acoplamiento es un auténtico fenómeno cuántico y relativista, es decir, un efecto de los diagramas Feynman de alto orden sobre la fuerza.

Dado que un acoplamiento en ejecución representa efectivamente los efectos cuánticos microscópicos, a menudo se le llama acoplamiento efectivo, en contraste con el acoplamiento desnudo (constante) presente en el lagrangiano o hamiltoniano.

Funciones beta

En la teoría cuántica de campos, una función beta, β(g), codifica la ejecución de un parámetro de acoplamiento, g. Se define por la relación

{displaystyle beta (g)=mu {frac {partial g}{partial mu }}={frac {partial g}{partial ln mu }},}

donde μ es la escala de energía del proceso físico dado. Si las funciones beta de una teoría cuántica de campos desaparecen, entonces la teoría es invariante de escala.

Los parámetros de acoplamiento de una teoría cuántica de campos pueden fluir incluso si la correspondiente teoría de campos clásica es invariante en escala. En este caso, la función beta distinta de cero nos dice que la invariancia de escala clásica es anómala.

QED y el polo Landau

Si una función beta es positiva, el acoplamiento correspondiente aumenta al aumentar la energía. Un ejemplo es la electrodinámica cuántica (QED), donde, utilizando la teoría de la perturbación, se descubre que la función beta es positiva. En particular, a bajas energías, α ≈ 1/137, mientras que a la escala del bosón Z, alrededor de 90 GeV, se mide α ≈ 1/127.

Además, la función beta perturbadora nos dice que el acoplamiento continúa aumentando, y QED se convierte en fuertemente unidos a alta energía. De hecho, el acoplamiento parece ser infinito en alguna energía finita. Este fenómeno fue notado por primera vez por Lev Landau, y se llama el polo de Landau. Sin embargo, no se puede esperar que la función beta perturbadora dé resultados precisos en un fuerte acoplamiento, por lo que es probable que el polo de Landau sea un artefacto de aplicar la teoría de la perturbación en una situación donde ya no es válida. El verdadero comportamiento de escalada ${displaystyle alpha }$ en grandes energías no se conoce.

QCD y libertad asintótica

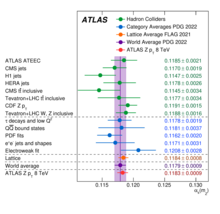
En las teorías de calibre no abelianas, la función beta puede ser negativa, como lo descubrieron por primera vez Frank Wilczek, David Politzer y David Gross. Un ejemplo de esto es la función beta de la cromodinámica cuántica (QCD) y, como resultado, el acoplamiento QCD disminuye a altas energías.

Además, el acoplamiento disminuye logarítmicamente, fenómeno conocido como libertad asintótica (cuyo descubrimiento fue galardonado con el Premio Nobel de Física en 2004). El acoplamiento disminuye aproximadamente como

{displaystyle alpha _{text{s}}(k^{2}) {stackrel {mathrm {def} }{=}} {frac {g_{text{s}}^{2}(k^{2})}{4pi }}approx {frac {1}{beta _{0}ln left({k^{2}}/{Lambda ^{2}}right)}},}

Donde β₀ es una primera computación constante de Wilczek, Gross y Politzer.

Por el contrario, el acoplamiento aumenta con la disminución de la energía. Esto significa que el acoplamiento se hace grande a bajas energías, y ya no se puede confiar en la teoría de la perturbación. Por lo tanto, el valor real de la constante de acoplamiento sólo se define a una escala de energía dada. En QCD, la escala de masa boson Z se elige normalmente, proporcionando un valor de la fuerte constante de acoplamiento de α_s(M_Z²) = 0.1179 ± 0,0010. En 2023 Atlas medido α_s(M_Z²) = 0.1183 ± 0.0009 el más preciso hasta ahora. Las mediciones más precisas provienen de cálculos de lattice QCD, estudios de decaimiento de tau-lepton, así como de la reinterpretación del espectro de impulso transversal del boson Z.

Escala QCD

En cromodinámica cuántica (QCD), la cantidad ≥ se llama Escala de QCD. El valor es ${displaystyle Lambda _{rm {MS}}=332pm 17{text{ MeV}}}$ para tres sabores "activos" quark, viz cuando la energía-momentum implicada en el proceso permite la producción de sólo los quarks arriba, abajo y extraño, pero no los quarks más pesados. Esto corresponde a energías inferiores a 1.275 GeV. En la energía superior, ≥ es más pequeño, por ejemplo. ${displaystyle Lambda _{rm {MS}}=210pm 14}$ MeV sobre la masa de quark inferior de alrededor 5 GeV. El significado de la escala mínima de tracción (MS)_MS se da en el artículo sobre transmutación dimensional. La relación de masa proton-to-electron está determinada principalmente por la escala QCD.

Teoría de cuerdas

Existe una situación notablemente diferente en la teoría de cuerdas, ya que incluye un dilatón. Un análisis del espectro de cuerdas muestra que este campo debe estar presente, ya sea en la cuerda bosónica o en el sector NS-NS de la supercuerda. Usando operadores de vértice, se puede ver que excitar este campo equivale a agregar un término a la acción donde un campo escalar se acopla al escalar de Ricci. Por lo tanto, este campo es una función completa de constantes de acoplamiento. Estas constantes de acoplamiento no son parámetros predeterminados, ajustables o universales; dependen del espacio y del tiempo de una manera que se determina dinámicamente. Las fuentes que describen el acoplamiento de la cuerda como si estuviera fijo generalmente se refieren al valor esperado de vacío. Esto puede tener cualquier valor en la teoría bosónica donde no hay superpotencial.

Contenido relacionado

Más resultados...