Combinación lineal

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Imágen de la combinación lineal de dos vectores — Combinación lineal de dos vectores en un espacio euclidiano

Una combinación lineal es una expresión matemática formada al multiplicar cada término de un conjunto por una constante y luego sumar los resultados obtenidos. Por ejemplo, una combinación lineal de las variables x, y podría representarse como ax + by, donde "a" y "b" son constantes. La combinación lineal es un concepto fundamental del álgebra lineal y los campos relacionados de las matemáticas.

Las combinaciones lineales poseen gran utilidad dentro del contexto de los espacios vectoriales sobre un campo. Estos espacios son estructuras matemáticas que proporcionan un marco para operaciones como la suma de vectores y la multiplicación de vectores por escalares. Las combinaciones lineales juegan un papel crucial en la comprensión y manipulación de estos espacios.

En general, la combinación lineal es una herramienta esencial de las matemáticas, permitiendo la construcción y el análisis de relaciones entre diferentes términos y variables. Su estudio y aplicación son indispensables no solo para el trabajo de áreas como el álgebra lineal y la teoría de vectores, sino en muchos otros campos de la matemática y la ciencia.

HSD

Definición formal

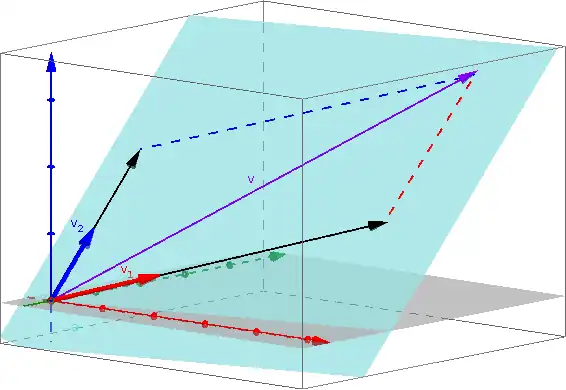
Sea V un espacio vectorial sobre el campo K. Como de costumbre, llamamos a los elementos de V vectores y a los elementos de K escalares. Si v ₁,..., v _n son vectores y a ₁,..., an son _escalares, entonces la combinación lineal de esos vectores con esos escalares como coeficientes es ${displaystyle a_{1}mathbf {v}_{1}+a_{2}mathbf {v}_{2}+a_{3}mathbf {v}_{3}+cdots +a_{ n}mathbf {v} _{n}.}$

Existe cierta ambigüedad en el uso del término "combinación lineal" en cuanto a si se refiere a la expresión oa su valor. En la mayoría de los casos se enfatiza el valor, como en la afirmación "el conjunto de todas las combinaciones lineales de v ₁,..., v _n siempre forma un subespacio". Sin embargo, también se podría decir "dos combinaciones lineales diferentes pueden tener el mismo valor", en cuyo caso la referencia es a la expresión. La sutil diferencia entre estos usos es la esencia de la noción de dependencia lineal: una familia F de vectores es linealmente independiente precisamente si cualquier combinación lineal de los vectores en F(como valor) es únicamente así (como expresión). En cualquier caso, aun cuando se vean como expresiones, todo lo que importa acerca de una combinación lineal es el coeficiente de cada v _i; modificaciones triviales como permutar los términos o agregar términos con coeficiente cero no producen combinaciones lineales distintas.

En una situación dada, K y V pueden especificarse explícitamente o pueden ser obvios por el contexto. En ese caso, a menudo hablamos de una combinación lineal de los vectores v ₁,..., v _n, con los coeficientes no especificados (excepto que deben pertenecer a K). O, si S es un subconjunto de V, podemos hablar de una combinación lineal de vectores en S, donde tanto los coeficientes como los vectores no están especificados, excepto que los vectores deben pertenecer al conjunto S (y los coeficientes deben pertenecer a K). Finalmente, podemos hablar simplemente de una combinación lineal, donde no se especifica nada (excepto que los vectores deben pertenecer a V y los coeficientes deben pertenecer a K); en este caso uno probablemente se esté refiriendo a la expresión, ya que cada vector en V es ciertamente el valor de alguna combinación lineal.

Tenga en cuenta que, por definición, una combinación lineal involucra solo una cantidad finita de vectores (excepto como se describe en Generalizaciones a continuación). Sin embargo, el conjunto S del que se toman los vectores (si se menciona uno) aún puede ser infinito; cada combinación lineal individual solo involucrará un número finito de vectores. Además, no hay razón para que n no pueda ser cero; en ese caso, declaramos por convención que el resultado de la combinación lineal es el vector cero en V.

Ejemplos y contraejemplos

Vectores euclidianos

Sea el campo K el conjunto R de los números reales, y sea el espacio vectorial V el espacio euclidiano R. Considere los vectores e ₁ = (1,0,0), e ₂ = (0,1,0) y e ₃ = (0,0,1). Entonces cualquier vector en R es una combinación lineal de e ₁, e ₂ y e ₃.

Para ver que esto es así, tome un vector arbitrario (a ₁, a ₂, a ₃) en R, y escriba: ${displaystyle {begin{alineado}(a_{1},a_{2},a_{3})&=(a_{1},0,0)+(0,a_{2},0)+(0,0,a_{3})\[6pt]&=a_{1}(1,0,0)+a_{2}(0,1,0)+a_{3}(0,0,1)\[6pt]&=a_{1}mathbf {e} _{1}+a_{2}mathbf {e} _{2}+a_{3}mathbf {e} _{3}. end{alineado}}}$

Funciones

Sea K el conjunto C de todos los números complejos, y sea V el conjunto C _C (R) de todas las funciones continuas desde la recta real R hasta el plano complejo C. Considere los vectores (funciones) f y g definidos por f (t):= e y g (t):= e. (Aquí, e es la base del logaritmo natural, aproximadamente 2,71828..., e i es la unidad imaginaria, una raíz cuadrada de −1). Algunas combinaciones lineales de f yg son:

${displaystyle cos t={tfrac {1}{2}},e^{it}+{tfrac {1}{2}},e^{-it}}$
${displaystyle 2sin t=(-i)e^{it}+(i)e^{-it}.}$

Por otro lado, la función constante 3 no es una combinación lineal de f y g. Para ver esto, suponga que 3 podría escribirse como una combinación lineal de e y e. Esto significa que existirían escalares complejos a y b tales que ae + be = 3 para todos los números reales t. Establecer t = 0 y t = π da las ecuaciones a + b = 3 y a + b = −3, y claramente esto no puede suceder. Ver la identidad de Euler.

Polinomios

Sea K R, C, o cualquier campo, y sea V el conjunto P de todos los polinomios con coeficientes tomados del campo K. Considere los vectores (polinomios) p ₁:= 1, p ₂:= x + 1 y p ₃:= x + x + 1.

¿Es el polinomio x − 1 una combinación lineal de p ₁, p ₂ y p ₃ ? Para averiguarlo, considere una combinación lineal arbitraria de estos vectores e intente ver cuándo es igual al vector deseado x − 1. Seleccionando coeficientes arbitrarios a ₁, a ₂ y a ₃, queremos ${displaystyle a_{1}(1)+a_{2}(x+1)+a_{3}(x^{2}+x+1)=x^{2}-1.}$

Multiplicando los polinomios, esto significa ${displaystyle (a_{1})+(a_{2}x+a_{2})+(a_{3}x^{2}+a_{3}x+a_{3})=x^{2 }-1}$

y reuniendo como potencias de x, obtenemos ${displaystyle a_{3}x^{2}+(a_{2}+a_{3})x+(a_{1}+a_{2}+a_{3})=1x^{2}+0x+(-1).}$

Dos polinomios son iguales si y solo si sus coeficientes correspondientes son iguales, por lo que podemos concluir ${displaystyle a_{3}=1,quad a_{2}+a_{3}=0,quad a_{1}+a_{2}+a_{3}=-1.}$

Este sistema de ecuaciones lineales se puede resolver fácilmente. Primero, la primera ecuación simplemente dice que un ₃ es 1. Sabiendo eso, podemos resolver la segunda ecuación para un ₂, que resulta en −1. Finalmente, la última ecuación nos dice que un ₁ también es −1. Por lo tanto, la única forma posible de obtener una combinación lineal es con estos coeficientes. Por cierto, ${displaystyle x^{2}-1=-1-(x+1)+(x^{2}+x+1)=-p_{1}-p_{2}+p_{3}}$

entonces x − 1 es una combinación lineal de p ₁, p ₂ y p ₃.

Por otro lado, ¿qué pasa con el polinomio x − 1? Si tratamos de hacer de este vector una combinación lineal de p ₁, p ₂ y p ₃, luego siguiendo el mismo proceso que antes, obtenemos la ecuación ${displaystyle {begin{alineado}&0x^{3}+a_{3}x^{2}+(a_{2}+a_{3})x+(a_{1}+a_{2}+a_{ 3})\[5pt]={}&1x^{3}+0x^{2}+0x+(-1).end{alineado}}}$

Sin embargo, cuando igualamos los coeficientes correspondientes en este caso, la ecuación para x es ${ estilo de visualización 0 = 1}$

que siempre es falso. Por lo tanto, no hay manera de que esto funcione, y x − 1 no es una combinación lineal de p ₁, p ₂ y p ₃.

Espacios vectoriales generados

Tome un campo arbitrario K, un espacio vectorial arbitrario V, y sean v ₁,..., v _n vectores (en V). Es interesante considerar el conjunto de todas las combinaciones lineales de estos vectores. Este conjunto se denomina tramo lineal (o simplemente tramo) de los vectores, digamos S = { v ₁,..., v _n }. Escribimos el lapso de S como lapso(S) o sp(S): ${displaystyle operatorname {span} (mathbf {v} _{1},ldots,mathbf {v} _{n}):={a_{1}mathbf {v} _{1}+ cdots +a_{n}mathbf {v} _{n}:a_{1},ldots,a_{n}in K}.}$

Independencia lineal

Supongamos que, para algunos conjuntos de vectores v ₁,..., v _n, un solo vector se puede escribir de dos maneras diferentes como una combinación lineal de ellos: ${displaystyle mathbf {v} =sum_{i}a_{i}mathbf {v}_{i}=sum_{i}b_{i}mathbf {v}_{i}{ texto{ donde }}a_{i}neq b_{i}.}$

Esto es equivalente, restando estos ( $c_{i}:=a_{i}-b_{i}$ ), a decir que una combinación no trivial es cero: ${displaystyle mathbf {0} =sum_{i}c_{i}mathbf {v}_{i}.}$

Si eso es posible, entonces v ₁,..., v _n se llaman linealmente dependientes; de lo contrario, son linealmente independientes. De manera similar, podemos hablar de dependencia o independencia lineal de un conjunto arbitrario S de vectores.

Si S es linealmente independiente y el intervalo de S es igual a V, entonces S es una base para V.

Combinaciones afines, cónicas y convexas

Al restringir los coeficientes utilizados en las combinaciones lineales, se pueden definir los conceptos relacionados de combinación afín, combinación cónica y combinación convexa, y las nociones asociadas de conjuntos cerrados bajo estas operaciones.

Tipo de combinación	Restricciones a los coeficientes	Nombre del conjunto	espacio modelo
Combinación lineal	sin restricciones	Subespacio vectorial	$mathbf{R} ^{n}$
combinación afín	${estilo de texto sum a_{i}=1}$	Subespacio afín	Hiperplano afín
combinación cónica	$a_{i}geq 0$	cono convexo	Cuadrante, octante u ortante
combinación convexa	$a_{i}geq 0$ y ${estilo de texto sum a_{i}=1}$	conjunto convexo	símplex

Debido a que estas son operaciones más restringidas, se cerrarán más subconjuntos debajo de ellas, por lo que los subconjuntos afines, los conos convexos y los conjuntos convexos son generalizaciones de subespacios vectoriales: un subespacio vectorial también es un subespacio afín, un cono convexo y un conjunto convexo, pero un conjunto convexo no necesita ser un subespacio vectorial, afín o un cono convexo.

Estos conceptos suelen surgir cuando se pueden tomar ciertas combinaciones lineales de objetos, pero no cualquiera: por ejemplo, las distribuciones de probabilidad son cerradas bajo combinación convexa (forman un conjunto convexo), pero no combinaciones cónicas o afines (o lineales), y medidas positivas se cierran bajo combinación cónica pero no afines o lineales; por lo tanto, uno define las medidas firmadas como el cierre lineal.

Las combinaciones lineales y afines se pueden definir sobre cualquier campo (o anillo), pero las combinaciones cónicas y convexas requieren una noción de "positivo" y, por lo tanto, solo se pueden definir sobre un campo ordenado (o anillo ordenado), generalmente los números reales.

Si solo se permite la multiplicación escalar, no la suma, se obtiene un cono (no necesariamente convexo); uno a menudo restringe la definición para permitir solo la multiplicación por escalares positivos.

Todos estos conceptos suelen definirse como subconjuntos de un espacio vectorial ambiental (excepto los espacios afines, que también se consideran "espacios vectoriales que olvidan el origen"), en lugar de axiomatizarse de forma independiente.

Teoría de los operad

De manera más abstracta, en el lenguaje de la teoría de los operad, uno puede considerar los espacios vectoriales como álgebras sobre la ópera $mathbf {R} ^{infty}$ (la suma directa infinita, por lo que solo un número finito de términos son distintos de cero; esto corresponde a solo tomar sumas finitas), que parametriza combinaciones lineales: el vector $(2,3,-5,0,puntos)$ por ejemplo corresponde a la combinación lineal ${displaystyle 2mathbf {v}_{1}+3mathbf {v}_{2}-5mathbf {v}_{3}+0mathbf {v}_{4}+cdots}$ . De manera similar, se pueden considerar combinaciones afines, combinaciones cónicas y combinaciones convexas para corresponder a los suboperados donde los términos suman 1, los términos son todos no negativos, o ambos, respectivamente. Gráficamente, estos son el hiperplano afín infinito, el hiperoctante infinito y el símplex infinito. Esto formaliza lo que se entiende por $mathbf{R} ^{n}$ o el simplex estándar siendo espacios modelo, y observaciones tales como que todo politopo convexo acotado es la imagen de un simplex. Aquí los suboperados corresponden a operaciones más restringidas y, por lo tanto, a teorías más generales.

Desde este punto de vista, podemos pensar en las combinaciones lineales como el tipo de operación más general en un espacio vectorial; decir que un espacio vectorial es un álgebra sobre la operada de combinaciones lineales es precisamente la afirmación de que todas las operaciones algebraicas posibles en un vector espacio son combinaciones lineales.

Las operaciones básicas de suma y multiplicación escalar, junto con la existencia de una identidad aditiva y de inversos aditivos, no pueden combinarse de forma más complicada que la combinación lineal genérica: las operaciones básicas son un conjunto generador para la operada de todas las combinaciones lineales.

En última instancia, este hecho se encuentra en el corazón de la utilidad de las combinaciones lineales en el estudio de los espacios vectoriales.

Generalizaciones

Si V es un espacio vectorial topológico, entonces puede haber una manera de dar sentido a ciertas combinaciones lineales infinitas, usando la topología de V. Por ejemplo, podríamos hablar de un ₁v ₁ + un ₂v ₂ + un ₃v ₃ + ⋯, continuando para siempre. Tales combinaciones lineales infinitas no siempre tienen sentido; los llamamos convergentes cuando lo hacen. Permitir más combinaciones lineales en este caso también puede conducir a un concepto diferente de tramo, independencia lineal y base. Los artículos sobre los diversos tipos de espacios vectoriales topológicos dan más detalles sobre estos.

Si K es un anillo conmutativo en lugar de un campo, entonces todo lo que se ha dicho anteriormente sobre las combinaciones lineales se generaliza para este caso sin cambios. La única diferencia es que a espacios como este los llamamos módulos V en lugar de espacios vectoriales. Si K es un anillo no conmutativo, entonces el concepto aún se generaliza, con una advertencia: dado que los módulos sobre anillos no conmutativos vienen en versiones izquierda y derecha, nuestras combinaciones lineales también pueden venir en cualquiera de estas versiones, lo que sea apropiado para el módulo dado. Esto es simplemente una cuestión de hacer la multiplicación escalar en el lado correcto.

Un giro más complicado surge cuando V es un bimódulo sobre dos anillos, K _L y K _R. En ese caso, la combinación lineal más general parece ${displaystyle a_{1}mathbf {v}_{1}b_{1}+cdots +a_{n}mathbf {v}_{n}b_{n}}$

donde a ₁,..., a _n pertenecen a K _L, b ₁,..., b _n pertenecen a K _R, y v ₁,…, v _n pertenecen a V.

Aplicaciones

Una aplicación importante de las combinaciones lineales es a las funciones de onda en la mecánica cuántica.

Contenido relacionado

Más resultados...