Máquina de estados finitos

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Modelo matemático de computación

Clases de automata

(Haga clic en cada capa obtiene un artículo sobre ese tema)

Una máquina de estados finitos (FSM) o autómata de estados finitos (FSA, plural: autómatas), autómatas finitos, o simplemente una máquina de estados, es un modelo matemático de computación. Es una máquina abstracta que puede estar exactamente en uno de un número finito de estados en un momento dado. El FSM puede cambiar de un estado a otro en respuesta a algunas entradas; el cambio de un estado a otro se llama transición. Una FSM se define mediante una lista de sus estados, su estado inicial y las entradas que desencadenan cada transición. Las máquinas de estados finitos son de dos tipos: máquinas de estados finitos deterministas y máquinas de estados finitos no deterministas. Se puede construir una máquina determinista de estados finitos equivalente a cualquier máquina no determinista.

El comportamiento de las máquinas de estado se puede observar en muchos dispositivos de la sociedad moderna que realizan una secuencia predeterminada de acciones según la secuencia de eventos que se les presentan. Ejemplos sencillos son las máquinas expendedoras, que dispensan productos cuando se deposita la combinación adecuada de monedas, los ascensores, cuya secuencia de paradas está determinada por los pisos solicitados por los pasajeros, los semáforos, que cambian de secuencia cuando los automóviles están esperando, y las cerraduras de combinación, que requieren la entrada de una secuencia de números en el orden correcto.

La máquina de estados finitos tiene menos poder de cómputo que otros modelos de cómputo, como la máquina de Turing. La distinción de poder computacional significa que hay tareas computacionales que una máquina de Turing puede hacer pero una FSM no puede. Esto se debe a que la memoria de un FSM está limitada por la cantidad de estados que tiene. Una máquina de estados finitos tiene el mismo poder computacional que una máquina de Turing que está restringida de tal manera que su cabeza solo puede realizar "leer" operaciones, y siempre tiene que moverse de izquierda a derecha. Las FSM se estudian en el campo más general de la teoría de autómatas.

Ejemplo: torniquete que funciona con monedas

Esquema de estado para un torntil

Un torntil

Un ejemplo de un mecanismo simple que puede ser modelado por una máquina de estado es un torniquete. Un torniquete, que se usa para controlar el acceso al metro y a las atracciones del parque de diversiones, es una puerta con tres brazos giratorios a la altura de la cintura, uno cruzando la entrada. Inicialmente, los brazos están bloqueados, bloqueando la entrada e impidiendo el paso de los clientes. Depositar una moneda o una ficha en una ranura del torniquete desbloquea los brazos, lo que permite que un solo cliente pase. Después del paso del cliente, los brazos se bloquean nuevamente hasta que se inserta otra moneda.

Considerado como una máquina de estados, el torniquete tiene dos posibles estados: Bloqueado y Desbloqueado. Hay dos posibles entradas que afectan a su estado: poner una moneda en la ranura (moneda) y empujar el brazo (empujar). En el estado bloqueado, empujar el brazo no tiene efecto; no importa cuántas veces se dé la entrada pulsar, permanece en el estado bloqueado. Poner una moneda, es decir, darle a la máquina una entrada de moneda, cambia el estado de Bloqueado a Desbloqueado. En el estado desbloqueado, poner monedas adicionales no tiene efecto; es decir, dar entradas de monedas adicionales no cambia el estado. Sin embargo, un cliente empujando a través de los brazos, dando una entrada de empuje, cambia el estado de nuevo a Bloqueado.

La máquina de estado del torniquete se puede representar mediante una tabla de transición de estado, que muestra para cada estado posible, las transiciones entre ellos (según las entradas proporcionadas a la máquina) y las salidas resultantes de cada entrada:

Estado actual	Input	Next State	Producto
Cerrado	moneda	Desbloqueado	Desbloquea el torno para que el cliente pueda atravesarlo.
Cerrado	empujar	Cerrado	Ninguno
Desbloqueado	moneda	Desbloqueado	Ninguno
Desbloqueado	empujar	Cerrado	Cuando el cliente ha atravesado, bloquea el torntil.

La máquina de estado del torniquete también se puede representar mediante un gráfico dirigido llamado diagrama de estado (arriba). Cada estado está representado por un nodo (círculo). Los bordes (flechas) muestran las transiciones de un estado a otro. Cada flecha está etiquetada con la entrada que desencadena esa transición. Una entrada que no provoca un cambio de estado (como una entrada de moneda en el Desbloqueado estado) está representado por una flecha circular que regresa al estado original. La flecha hacia el nodo Bloqueado desde el punto negro indica que es el estado inicial.

Conceptos y terminología

Un estado es una descripción del estado de un sistema que está esperando para ejecutar una transición. Una transición es un conjunto de acciones a ejecutar cuando se cumple una condición o cuando se recibe un evento. Por ejemplo, al usar un sistema de audio para escuchar la radio (el sistema está en el estado "radio"), al recibir un mensaje "siguiente" el estímulo da como resultado pasar a la siguiente estación. Cuando el sistema está en modo "CD" estado, el "siguiente" el estímulo da como resultado pasar a la siguiente pista. Estímulos idénticos desencadenan acciones diferentes según el estado actual.

En algunas representaciones de máquinas de estados finitos, también es posible asociar acciones con un estado:

una acción de entrada: realizada al entrar el estado, y
una acción de salida: realizada cuando salga el estado.

Representaciones

Ejemplo de gráfico UML (horno tostador)

Fig. 2 ejemplo de máquina de estado SDL

Fig. 3 Ejemplo de una simple máquina de estado finito

Tabla de estado/evento

Se utilizan varios tipos de tablas de transición de estado. La representación más común se muestra a continuación: la combinación del estado actual (por ejemplo, B) y la entrada (por ejemplo, Y) muestra el siguiente estado (por ejemplo, C). La información de la acción completa no se describe directamente en la tabla y solo se puede agregar mediante notas al pie. Es posible una definición de FSM que incluya la información completa de la acción utilizando tablas de estado (ver también máquina virtual de estado finito).

State-transition table
Corriente estado Input	Estado A	Estado B	Estado C
Entrada X	...	...	...
Entrada Y	...	Estado C	...
Entrada Z	...	...	...

Máquinas de estado UML

El lenguaje de modelado unificado tiene una notación para describir máquinas de estado. Las máquinas de estado UML superan las limitaciones de las máquinas de estado finito tradicionales y conservan sus principales beneficios. Las máquinas de estado UML introducen los nuevos conceptos de estados anidados jerárquicamente y regiones ortogonales, al tiempo que amplían la noción de acciones. Las máquinas de estado UML tienen las características tanto de las máquinas Mealy como de las máquinas Moore. Admiten acciones que dependen tanto del estado del sistema como del evento desencadenante, como en las máquinas Mealy, así como acciones de entrada y salida, que están asociadas con estados en lugar de transiciones, como en las máquinas Moore.

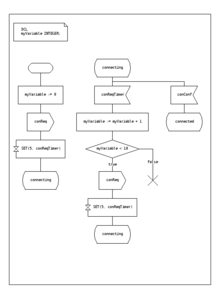
Máquinas de estado SDL

El lenguaje de especificación y descripción es un estándar de la UIT que incluye símbolos gráficos para describir acciones en la transición:

enviar un evento
recibir un evento
empezar un temporizador
cancelar un temporizador
iniciar otra máquina estatal concurrente
decisión

SDL incorpora tipos de datos básicos llamados "Tipos de datos abstractos", un lenguaje de acción y una semántica de ejecución para hacer que la máquina de estado finito sea ejecutable.

Otros diagramas de estado

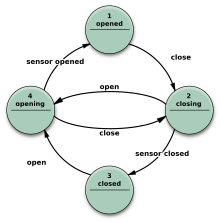
Existe una gran cantidad de variantes para representar una FSM como la de la figura 3.

Uso

Además de su uso en el modelado de sistemas reactivos presentado aquí, las máquinas de estado finito son importantes en muchas áreas diferentes, incluidas la ingeniería eléctrica, la lingüística, la informática, la filosofía, la biología, las matemáticas, la programación de videojuegos y la lógica. Las máquinas de estados finitos son una clase de autómatas estudiados en la teoría de autómatas y la teoría de la computación. En informática, las máquinas de estado finito se utilizan ampliamente en el modelado del comportamiento de aplicaciones (teoría de control), diseño de sistemas digitales de hardware, ingeniería de software, compiladores, protocolos de red y lingüística computacional.

Clasificación

Las máquinas de estados finitos se pueden subdividir en aceptadores, clasificadores, transductores y secuenciadores.

Aceptores

Fig. 4: Aceptador FSM: persiguiendo la cadena "nice".

Fig. 5: Representación de un aceptador; este ejemplo muestra uno que determina si un número binario tiene un número uniforme de 0s, donde S₁ es un aceptando estado y S₂ es un Estado no aceptado.

Aceptores (también llamados detectores o reconocedores) producen una salida binaria, indicando si la entrada recibida es aceptada o no. Cada estado de un aceptador es aceptar o no aceptar. Una vez que se han recibido todas las entradas, si el estado actual es un estado de aceptación, se acepta la entrada; de lo contrario, se rechaza. Como regla, la entrada es una secuencia de símbolos (caracteres); No se utilizan acciones. El estado inicial también puede ser un estado de aceptación, en cuyo caso el aceptador acepta la cadena vacía. El ejemplo de la figura 4 muestra un aceptador que acepta la cadena "agradable". En este aceptador, el único estado de aceptación es el estado 7.

Un conjunto (posiblemente infinito) de secuencias de símbolos, llamado lenguaje formal, es un lenguaje regular si hay algún aceptador que acepte exactamente ese conjunto. Por ejemplo, el conjunto de cadenas binarias con un número par de ceros es un lenguaje regular (cf. Fig. 5), mientras que el conjunto de todas las cadenas cuya longitud es un número primo no lo es.

Un aceptador también podría describirse como la definición de un idioma que contendría todas las cadenas aceptadas por el aceptador pero ninguna de las rechazadas; ese lenguaje es aceptado por el aceptante. Por definición, los lenguajes aceptados por los aceptantes son los lenguajes regulares.

El problema de determinar el lenguaje aceptado por un aceptador dado es una instancia del problema del camino algebraico, en sí mismo una generalización del problema del camino más corto a gráficos con bordes ponderados por los elementos de un semiring (arbitrario).

En la Fig. 5 aparece un ejemplo de un estado de aceptación: un autómata finito determinista (DFA) que detecta si la cadena de entrada binaria contiene un número par de ceros.

S₁ (que también es el estado inicial) indica el estado en el que se ha ingresado un número par de ceros. S₁ es por lo tanto un estado de aceptación. Este aceptador terminará en un estado de aceptación, si la cadena binaria contiene un número par de ceros (incluida cualquier cadena binaria que no contenga ceros). Ejemplos de cadenas aceptadas por este aceptador son ε (la cadena vacía), 1, 11, 11..., 00, 010, 1010, 10110, etc.

Clasificadores

Los clasificadores son una generalización de aceptadores que producen una salida n-aria donde n es estrictamente mayor que dos.

Transductores

Fig. 6 Transductor FSM: Ejemplo de modelo Moore

Fig. 7 Transductor FSM: Ejemplo de modelo Mealy

Los

transductores producen una salida basada en una entrada dada y/o un estado mediante acciones. Se utilizan para aplicaciones de control y en el campo de la lingüística computacional.

En las aplicaciones de control se distinguen dos tipos:

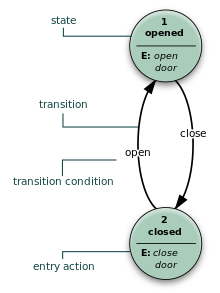
Máquina de Moore: El FSM sólo utiliza acciones de entrada, es decir, la salida depende sólo del estado. La ventaja del modelo Moore es una simplificación del comportamiento. Considere una puerta de ascensor. La máquina estatal reconoce dos comandos: "command_open" y "command_close", que desencadenan cambios estatales. La acción de entrada (E:) en el estado "Abrir" comienza un motor que abre la puerta, la acción de entrada en el estado "Cerrar" comienza un motor en la otra dirección que cierra la puerta. Estados "Abrir" y "Closed" detienen el motor cuando se abre o cierra completamente. Indican al mundo exterior (por ejemplo, a otras máquinas estatales) la situación: "la puerta está abierta" o "la puerta está cerrada".

Mealy machine: El FSM también utiliza acciones de entrada, es decir, la salida depende de entrada y estado. El uso de una FSM Mealy conduce a menudo a una reducción del número de estados. El ejemplo en la figura 7 muestra un Mealy FSM que implementa el mismo comportamiento que en el ejemplo Moore (el comportamiento depende del modelo de ejecución FSM implementado y funcionará, por ejemplo, para FSM virtual pero no para FSM impulsado por eventos). Hay dos acciones de entrada (I:): "iniciar el motor para cerrar la puerta si comando_close llega" y "iniciar el motor en la otra dirección para abrir la puerta si comando_open llega". Los estados intermedios "abrir" y "cerrar" no se muestran.

Secuenciadores

Secuenciadores (también llamados generadores) son una subclase de aceptores y transductores que tienen un alfabeto de entrada de una sola letra. Producen solo una secuencia, que puede verse como una secuencia de salida de salidas de aceptor o transductor.

Determinismo

Otra distinción es entre autómatas deterministas (DFA) y no deterministas (NFA, GNFA). En un autómata determinista, cada estado tiene exactamente una transición para cada entrada posible. En un autómata no determinista, una entrada puede conducir a una, más de una o ninguna transición para un estado dado. El algoritmo de construcción powerset puede transformar cualquier autómata no determinista en un autómata determinista (generalmente más complejo) con una funcionalidad idéntica.

Una máquina de estados finitos con un solo estado se denomina "FSM combinatoria". Solo permite acciones sobre la transición a un estado. Este concepto es útil en los casos en que se requiere que varias máquinas de estado finito trabajen juntas, y cuando es conveniente considerar una pieza puramente combinatoria como una forma de FSM para adaptarse a las herramientas de diseño.

Semántica alternativa

Hay otros conjuntos de semántica disponibles para representar máquinas de estado. Por ejemplo, existen herramientas para modelar y diseñar la lógica de los controladores integrados. Combinan máquinas de estado jerárquicas (que suelen tener más de un estado actual), gráficos de flujo y tablas de verdad en un solo lenguaje, lo que da como resultado un formalismo y un conjunto de semánticas diferentes. Estos gráficos, al igual que las máquinas de estado originales de Harel, admiten estados anidados jerárquicamente, regiones ortogonales, acciones de estado y acciones de transición.

Modelo matemático

De acuerdo con la clasificación general, se encuentran las siguientes definiciones formales.

A deterministic finite-state machine o deterministic finite-state acceptor es un quintuple $(SigmaS,s_{0},deltaF)$ , donde:

$Sigma$ es el alfabeto de entrada (un conjunto no vacío finito de símbolos);
$S$ es un conjunto finito de estados no vacíos;
$s_{0}$ es un estado inicial, un elemento $S$ ;
$delta$ es la función estatal-transición: $delta:Stimes Sigma rightarrow S$ (en un autómata finita no determinista sería $delta:Stimes Sigma rightarrow {mathcal {P}}(S)$ , es decir. $delta$ d) Devolvería un conjunto de estados;
$F$ es el conjunto de estados finales, un subconjunto (posiblemente vacío) $S$ .

Para las FSM tanto deterministas como no deterministas, es convencional permitir $delta$ para ser una función parcial, es decir. ${displaystyle delta (s,x)}$ no tiene que ser definido para cada combinación de ${displaystyle sin S}$ y $xin Sigma$ . Si un FSM $M$ está en un estado $s$ , el próximo símbolo es $x$ y ${displaystyle delta (s,x)}$ no se define, entonces $M$ puede anunciar un error (es decir, rechazar la entrada). Esto es útil en definiciones de máquinas de estado general, pero menos útil al transformar la máquina. Algunos algoritmos en su forma predeterminada pueden requerir funciones totales.

Una máquina de estados finitos tiene la misma potencia computacional que una máquina de Turing que está restringida de tal manera que su cabeza solo puede realizar "leer" operaciones, y siempre tiene que moverse de izquierda a derecha. Es decir, cada lenguaje formal aceptado por una máquina de estados finitos es aceptado por una especie de máquina de Turing restringida, y viceversa.

A transductor de estado finito es un sextuple $(SigmaGammaS,s_{0},deltaomega)$ , donde:

$Sigma$ es el alfabeto de entrada (un conjunto no vacío finito de símbolos);
$Gamma$ es el alfabeto de salida (un conjunto no vacío finito de símbolos);
$S$ es un conjunto finito de estados no vacíos;
$s_{0}$ es el estado inicial, un elemento $S$ ;
$delta$ es la función estatal-transición: $delta:Stimes Sigma rightarrow S$ ;
$omega$ es la función de salida.

Si la función de salida depende del estado y el símbolo de entrada ( $omega:Stimes Sigma rightarrow Gamma$ ) que la definición corresponde a la Modelo de medición, y se puede modelar como una máquina Mealy. Si la función de salida depende sólo del estado ( $omega:Srightarrow Gamma$ ) que la definición corresponde a la Modelo de Moore, y puede ser modelado como una máquina Moore. Una máquina de estado finito sin función de salida en absoluto se conoce como un sistema semiautomatono o de transición.

Si ignoramos el primer símbolo de salida de una máquina Moore, ${displaystyle omega (s_{0})}$ , entonces se puede convertir fácilmente a un equivalente de salida Mealy máquina estableciendo la función de salida de cada transición Mealy (es decir, etiquetando cada borde) con el símbolo de salida dado del estado Moore destino. La transformación conversa es menos directa porque un estado de máquina de Mealy puede tener diferentes etiquetas de salida en sus transiciones entrantes (edges). Cada estado debe dividirse en múltiples estados de la máquina Moore, uno para cada símbolo de salida del incidente.

Optimización

Optimizar una FSM significa encontrar una máquina con la cantidad mínima de estados que realice la misma función. El algoritmo conocido más rápido que hace esto es el algoritmo de minimización de Hopcroft. Otras técnicas incluyen el uso de una tabla de implicación o el procedimiento de reducción de Moore. Además, las FSA acíclicas se pueden minimizar en tiempo lineal.

Implementación

Aplicaciones de hardware

Fig. 9 El diagrama de circuito para un contador TTL de 4 bits, un tipo de máquina estatal

En un circuito digital, se puede construir un FSM usando un dispositivo lógico programable, un controlador lógico programable, puertas lógicas y biestables o relés. Más específicamente, una implementación de hardware requiere un registro para almacenar variables de estado, un bloque de lógica combinacional que determina la transición de estado y un segundo bloque de lógica combinacional que determina la salida de una FSM. Una de las implementaciones de hardware clásicas es el controlador Richards.

En una máquina de Medvedev, la salida se conecta directamente a los flip-flops de estado, lo que minimiza el tiempo de retardo entre los flip-flops y la salida.

La codificación de estado a través de máquinas de estado de bajo consumo puede optimizarse para minimizar el consumo de energía.

Aplicaciones de software

Los siguientes conceptos se usan comúnmente para crear aplicaciones de software con máquinas de estado finito:

Programación basada en la automata
Máquina de estado finito impulsada por el evento
Máquina del estado finito virtual
Patrón de diseño del Estado

Máquinas de estado finito y compiladores

Los autómatas finitos se utilizan a menudo en la interfaz de los compiladores de lenguajes de programación. Tal interfaz puede comprender varias máquinas de estado finito que implementan un analizador léxico y un analizador sintáctico. A partir de una secuencia de caracteres, el analizador léxico genera una secuencia de tokens de idioma (como palabras reservadas, literales e identificadores) a partir de los cuales el analizador genera un árbol de sintaxis. El analizador léxico y el analizador manejan las partes regulares y libres de contexto de la gramática del lenguaje de programación.

Contenido relacionado

Más resultados...