Autómata finito no determinista

En la teoría de los autómatas, una máquina de estados finitos se llama autómata finito determinista (DFA), si

• cada una de sus transiciones es única determinado por su estado fuente y símbolo de entrada, y
• leer un símbolo de entrada es necesario para cada transición estatal.

Un autómata finito no determinista (NFA), o una máquina de estados finitos no determinista, no necesita obedecer estas restricciones. En particular, cada AFD es también un AFN. A veces, el término NFA se utiliza en un sentido más estricto, refiriéndose a una NFA que no es un DFA, pero no en este artículo.

Utilizando el algoritmo de construcción de subconjuntos, cada NFA se puede traducir a un DFA equivalente; es decir, un DFA que reconoce el mismo lenguaje formal. Al igual que los DFA, los NFA solo reconocen lenguajes regulares.

Las NFA fueron introducidas en 1959 por Michael O. Rabin y Dana Scott, quienes también demostraron su equivalencia con las DFA. Los NFA se utilizan en la implementación de expresiones regulares: la construcción de Thompson es un algoritmo para compilar una expresión regular en un NFA que puede realizar de manera eficiente la coincidencia de patrones en cadenas. Por el contrario, el algoritmo de Kleene se puede utilizar para convertir un NFA en una expresión regular (cuyo tamaño es generalmente exponencial en el autómata de entrada).

Los NFA se han generalizado de múltiples maneras, por ejemplo, autómatas finitos no deterministas con movimientos ε, transductores de estado finito, autómatas pushdown, autómatas alternos, autómatas ω y autómatas probabilísticos. Además de los DFA, otros casos especiales conocidos de NFA son autómatas finitos inequívocos (UFA) y autómatas finitos de autoverificación (SVFA).

Introducción informal

Hay dos formas de describir el comportamiento de una NFA y ambas son equivalentes. La primera forma hace uso del no determinismo en nombre de una NFA. Para cada símbolo de entrada, la NFA pasa a un nuevo estado hasta que se hayan consumido todos los símbolos de entrada. En cada paso, el autómata “elige” de manera no determinista; una de las transiciones aplicables. Si existe al menos una "carrera de la suerte", es decir, alguna secuencia de elecciones que conducen a un estado de aceptación después de consumir completamente la entrada, se acepta. De lo contrario, es decir, si ninguna secuencia de elección puede consumir toda la entrada y conducir a un estado de aceptación, la entrada se rechaza.

En la segunda forma, la NFA consume una cadena de símbolos de entrada, uno por uno. En cada paso, siempre que sean aplicables dos o más transiciones, "clona" en muchas copias apropiadas, cada una siguiendo una transición diferente. Si no se aplica ninguna transición, la copia actual se encuentra en un callejón sin salida y "muere". Si, después de consumir la entrada completa, alguna de las copias está en estado de aceptación, la entrada se acepta; de lo contrario, se rechaza.

Definición formal

Para una introducción más elemental de la definición formal, consulte la teoría de los autómatas.

Autómata

An NFA está representado formalmente por un 5-tuple, ${displaystyle (Q,Sigmadeltaq_{0},F)}$, que consiste en

• un conjunto finito de estados ${displaystyle Q}$.
• un conjunto finito de símbolos de entrada ${displaystyle Sigma$.
• a) Función de transición ${displaystyle delta }$: ${displaystyle Qtimes Sigma rightarrow {Mathcal {P}(Q)}$.
• an inicial (o Empieza) estado ${displaystyle q_{0}in Q}$.
• un conjunto de estados ${displaystyle F}$ distinguido aceptar (o final) estados ${displaystyle Fsubseteq Q}$.

Aquí, ${displaystyle {mathcal {}(Q)}$ denota el conjunto de poder ${displaystyle Q}$.

Idioma reconocido

Given an NFA ${displaystyle M=(Q,Sigmadeltaq_{0},F)}$, su idioma reconocido es denotado por ${displaystyle L(M)}$, y se define como el conjunto de todas las cuerdas sobre el alfabeto ${displaystyle Sigma$ que son aceptados ${displaystyle M}$.

Loosely correspondiente a las explicaciones informales anteriores, hay varias definiciones formales equivalentes de una cadena ${displaystyle...$ aceptada ${displaystyle M}$:

• ${displaystyle w}$ es aceptado si una secuencia de estados, ${displaystyle ¿Qué?$, existe en ${displaystyle Q}$ tal que:
  1. ${displaystyle R_{0}=q_{0}$
  2. ${displaystyle r_{i+1}in delta (r_{i},a_{i+1}}$Para ${displaystyle i=0,ldotsn-1}$
  3. ${displaystyle r_{n}in F.$.

En palabras, la primera condición dice que la máquina comienza en el estado inicial ${displaystyle q_{0}$. La segunda condición dice que dado cada carácter de cuerda ${displaystyle w}$, la máquina pasará de estado a estado según la función de transición ${displaystyle delta }$. La última condición dice que la máquina acepta ${displaystyle w}$ si la última entrada de ${displaystyle w}$ hace que la máquina se detenga en uno de los estados aceptados. Para ${displaystyle w}$ para ser aceptado por ${displaystyle M}$, no es necesario que cada secuencia estatal termine en un estado de aceptación, es suficiente si uno lo hace. De lo contrario, i.e. si es imposible para nada obtener de ${displaystyle q_{0}$ a un estado desde ${displaystyle F}$ by following ${displaystyle w}$, se dice que el autómata rechazos la cuerda. El conjunto de cuerdas ${displaystyle M}$ acepta es el idioma reconocida por ${displaystyle M}$ y este lenguaje es denotado ${displaystyle L(M)}$.

• Alternativamente, ${displaystyle w}$ es aceptado si ${displaystyle delta ^{*}(q_{0},w)cap Fnot =emptyset }$, donde ${displaystyle delta ^{*}: Qtimes Sigma ^{*}rightarrow {mathcal}(Q)}$ se define recursivamente por:
  1. ${displaystyle delta ^{*}(r,epsilon)={r}$ Donde ${displaystyle epsilon }$ es la cuerda vacía, y
  2. ${displaystyle delta ^{*}(r,xa)=bigcup _{r'in delta ^{*}(r,x)}delta (r'a)}$ para todos ${displaystyle xin Sigma ^{*},ain Sigma }$.

En palabras, ${displaystyle delta ^{*}(r,x)}$ es el conjunto de todos los estados accesibles desde el estado ${displaystyle r}$ consumiendo la cuerda ${displaystyle x}$. La cuerda ${displaystyle w}$ es aceptado si algún estado aceptado en ${displaystyle F}$ puede ser alcanzado desde el estado inicial ${displaystyle q_{0}$ por consumir ${displaystyle w}$.

Estado inicial

La definición de autómata anterior utiliza un estado inicial único, que no es necesario. A veces, los NFA se definen con un conjunto de estados iniciales. Existe una construcción sencilla que traduce un NFA con múltiples estados iniciales a un NFA con un único estado inicial, lo que proporciona una notación conveniente.

Ejemplo

El siguiente autómata ${displaystyle M}$, con un alfabeto binario, determina si la entrada termina con un 1. Vamos. ${displaystyle M=({p,q},{0,1},deltap,{q})}$ Donde la función de transición ${displaystyle delta }$ puede definirse por esta tabla de transición estatal (cf. imagen superior izquierda):

Input Estado	0	1
${displaystyle p}$	${displaystyle {}}$	${displaystyle {p,q}}$
${displaystyle q}$	${displaystyle emptyset }$	${displaystyle emptyset }$

Desde el set ${displaystyle delta (p,1)}$ contiene más de un estado, ${displaystyle M}$ no es determinista. El idioma de ${displaystyle M}$ puede ser descrito por el lenguaje regular dado por la expresión regular (0|1)*1.

Todas las secuencias de estado posibles para la cadena de entrada "1011" se muestran en la imagen inferior. La cuerda es aceptada por ${displaystyle M}$ ya que una secuencia de estado satisface la definición anterior; no importa que otras secuencias no lo hagan. La imagen puede ser interpretada en un par de formas:

• En términos de la explicación anterior "de mala suerte", cada camino en la imagen denota una secuencia de opciones de ${displaystyle M}$.
• En términos de la explicación "cerrar", cada columna vertical muestra todos los clones de ${displaystyle M}$ en un momento dado en el tiempo, múltiples flechas que emanan de un nodo indican la clonación, un nodo sin flechas emanantes indicando la "muerte" de un clon.

La viabilidad de leer la misma imagen de dos maneras también indica la equivalencia de ambas explicaciones anteriores.

• Considerando la primera de las definiciones formales anteriores, "1011" es aceptada ya que al leerlo ${displaystyle M}$ puede atravesar la secuencia del estado ${displaystyle langle r_{0},r_{1},r_{2},r_{4}rangle =langle p,p,p,p,p,qrangle }$, que satisface las condiciones 1 a 3.
• En cuanto a la segunda definición formal, el cálculo inferior muestra que ${displaystyle delta ^{*}(p,epsilon)=p}$, por consiguiente ${displaystyle delta ^{*}(p,1)=delta (p,1)=p,q}$, por consiguiente ${displaystyle delta ^{*}(p,10)=delta (p,0)cup delta (q,0)={p}cup {}$, por consiguiente ${displaystyle delta ^{*}(p,101)=delta (p,1)=p,q}$, y por lo tanto ${displaystyle delta ^{*}(p,1011)=delta (p,1)cup delta (q,1)={p,q}cup {}$; ya que ese conjunto no se descompone ${displaystyle {q}}$, se acepta la cuerda "1011".

En contraste, la cadena "10" es rechazada por ${displaystyle M}$ (todas las posibles secuencias de estado para esa entrada se muestran en la imagen superior derecha), ya que no hay manera de llegar al único estado de aceptación, ${displaystyle q}$, leyendo el símbolo final 0. Mientras tanto ${displaystyle q}$ se puede alcanzar después de consumir la inicial "1", esto no significa que la entrada "10" sea aceptada, sino que significa que se aceptaría una cadena de entrada "1".

Equivalencia con DFA

Un autómata finito determinista (DFA) puede verse como un tipo especial de NFA, en el que para cada estado y símbolo, la función de transición tiene exactamente un estado. Por tanto, está claro que todo lenguaje formal que pueda ser reconocido por una DFA puede ser reconocido por una NFA.

Por el contrario, para cada NFA, existe un DFA que reconoce el mismo lenguaje formal. El DFA se puede construir utilizando la construcción powerset.

Este resultado muestra que las NFA, a pesar de su flexibilidad adicional, no pueden reconocer idiomas que no pueden ser reconocidos por algunas DFA. También es importante en la práctica para convertir NFA más fáciles de construir en DFA ejecutables de manera más eficiente. Sin embargo, si la NFA tiene n estados, la DFA resultante puede tener hasta 2ⁿ estados, lo que a veces hace que la construcción no sea práctica para NFA grandes..

NFA con movimientos ε

El autómata finito no determinista con ε-movimientos (NFA-ε) es una generalización adicional de NFA. En este tipo de autómata, la función de transición se define adicionalmente en la cadena vacía ε. Una transición sin consumir un símbolo de entrada se denomina transición ε y se representa en los diagramas de estado mediante una flecha denominada "ε". Las transiciones ε proporcionan una manera conveniente de modelar sistemas cuyos estados actuales no se conocen con precisión: es decir, si estamos modelando un sistema y no está claro si el estado actual (después de procesar alguna cadena de entrada) debe ser q o q', entonces podemos agregar una transición ε entre estos dos estados, poniendo así el autómata en ambos estados simultáneamente.

Definición formal

An NFA-ε está representado formalmente por un 5-tuple, ${displaystyle (Q,Sigmadeltaq_{0},F)}$, que consiste en

• un conjunto finito de estados ${displaystyle Q}$
• un conjunto finito de símbolos de entrada llamado el alfabeto ${displaystyle Sigma$
• a) Función de transición ${displaystyle delta: Qtimes (Sigma cup {epsilon })right {arrowmathcal {P}(Q)}$
• an inicial (o comienzo) estado ${displaystyle q_{0}in Q}$
• un conjunto de estados ${displaystyle F}$ distinguido como estados aceptados (o finales) ${displaystyle Fsubseteq Q}$.

Aquí, ${displaystyle {mathcal {}(Q)}$ denota el conjunto de poder ${displaystyle Q}$ y ${displaystyle epsilon }$ denota cuerda vacía.

Ε-cierre de un estado o conjunto de estados

Para un estado ${displaystyle qin Q}$, vamos ${displaystyle E(q)}$ denota el conjunto de estados que son accesibles ${displaystyle q}$ por las siguientes transiciones ε en la función de transición ${displaystyle delta }$, es decir, ${displaystyle pin E(q)}$ si hay una secuencia de estados ${displaystyle q_{1},...,q_{k}$ tales que

• ${displaystyle q_{1}=q}$,
• ${displaystyle q_{i+1}in delta (q_{i},varepsilon)}$ para cada uno ${displaystyle 1leq iSeguido]$, y
• ${displaystyle q_{k}=p}$.

${displaystyle E(q)}$ es conocido como cierre de epsilon(también ε-closure) de ${displaystyle q}$.

The ε-closure of a set ${displaystyle P}$ de estados de un NFA se define como el conjunto de estados alcanzables de cualquier estado en ${displaystyle P}$ ε-transitions. Formalmente, para ${displaystyle Psubseteq Q}$, definir ${displaystyle E(P)=bigcup limits _{qin P}E(q)}$.

Función de transición extendida

Similar al NFA sin movimientos ε, la función de transición ${displaystyle delta }$ of an NFA-ε can be extended to strings. Informalmente, ${displaystyle delta ^{*}(q,w)}$ denota el conjunto de todos los estados que el autómata pudo haber alcanzado al comenzar en estado ${displaystyle qin Q}$ y leer la cuerda ${displaystyle win Sigma ^{*}$La función ${displaystyle delta ^{*}: Qtimes Sigma ^{*}rightarrow {mathcal}(Q)}$ puede definirse recursivamente como sigue.

• ${displaystyle delta ^{*}(q,varepsilon)=E(q)}$, por cada estado ${displaystyle qin Q,}$ y dónde ${displaystyle E}$ denota el cierre de la epsilon;

Informalmente: Leer la cuerda vacía puede conducir el autómata del estado ${displaystyle q}$ a cualquier estado del cierre de epsilon ${displaystyle q.}$

• ${textstyle delta ^{*}(q,wa)=bigcup _{rin delta ^{*}(q,w)}E(delta (r,a)}}$ para cada estado ${displaystyle qin Q,}$ cada cadena ${displaystyle win Sigma ^{*}$ y cada símbolo ${displaystyle ain Sigma.}$

Informalmente: Leyendo la cuerda ${displaystyle w}$ puede conducir el autómata del estado ${displaystyle q}$ a cualquier estado ${displaystyle r}$ en el conjunto recurrentemente computado ${displaystyle delta ^{*}(q,w)}$; después de eso, leer el símbolo ${displaystyle a}$ puede conducir desde ${displaystyle r}$ a cualquier estado en el cierre de epsilon ${displaystyle delta (r,a). }$

Se dice que el autómata acepta una cadena ${displaystyle w}$ si

${displaystyle delta ^{*}(q_{0},w)cap Fneq emptyset}$

es decir, si la lectura ${displaystyle w}$ puede conducir el autómata desde su estado de inicio ${displaystyle q_{0}$ a algunos estados aceptados en ${displaystyle F.}$

Ejemplo

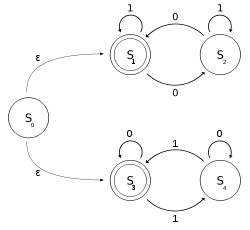
Vamos. ${displaystyle M}$ ser un NFA-ε, con un alfabeto binario, que determina si la entrada contiene un número uniforme de 0s o un número uniforme de 1s. Tenga en cuenta que 0 ocurrencias es incluso un número de ocurrencias también.

En notación formal, sea

$${displaystyle M=({0},S_{1},S_{2},S_{3},S_{4}},{0,1},deltaS_{0},{S_{1},S_{3}})}$$

${displaystyle delta }$

${displaystyle M}$ puede considerarse como la unión de dos DFA: uno con estados ${displaystyle {S_{1},S_{2}}}$ y el otro con estados ${displaystyle {S_{3},S_{4}}$. El idioma de ${displaystyle M}$ puede ser descrito por el lenguaje regular dado por esta expresión regular ${displaystyle (1^{*}01^{*}0)}cup (0^{*}10^{*}*}*}{*}}}*}}*$. Definimos ${displaystyle M}$ usando ε-moves pero ${displaystyle M}$ se puede definir sin utilizar ε-moves.

Equivalencia con NFA

Para mostrar que NFA-ε es equivalente a NFA, primero tenga en cuenta que NFA es un caso especial de NFA-ε, por lo que queda por mostrar que para cada NFA-ε existe un NFA equivalente.

Dado un NFA con movimientos de epsilón ${displaystyle M=(Q,Sigmadeltaq_{0},F),}$definir un NFA ${displaystyle M'=(Q,Sigmadelta ',q_{0},F'),}$ Donde

${displaystyle F'={begin{cases}Fcup {q_{0}} {text{ if }E(q_{0})cap Fneq {}\F simultáneamente{ otherwise }\\end{cases}}}\\fnMicrosoft Sans Serif}$

y

${displaystyle delta '(q,a)=delta ^{*}(q,a)}$ para cada estado ${displaystyle qin Q}$ y cada símbolo ${displaystyle ain Sigma}$ utilizando la función de transición ampliada ${displaystyle delta ^{*}$ definido anteriormente.

Uno tiene que distinguir las funciones de transición ${displaystyle M}$ y ${displaystyle M',}$ viz. ${displaystyle delta }$ y ${displaystyle delta,}$ y sus extensiones a cadenas, ${displaystyle delta }$ y ${displaystyle delta '^{*}$ respectivamente. Por construcción, ${displaystyle M'}$ no tiene ε-transitions.

Uno puede probar que ${displaystyle delta '^{*}(q_{0},w)=delta ^{*}(q_{0},w)}$ para cada cadena ${displaystyle wneq varepsilon }$, por inducción sobre la longitud ${displaystyle w.}$

Basado en esto, se puede demostrar que ${displaystyle delta '^{*}(q_{0},w)cap F'neq{}$ si, y sólo si, ${displaystyle delta ^{*}(q_{0},w)cap Fneq{}$ para cada cadena ${displaystyle win Sigma ^{*}$

• Si ${displaystyle w=varepsilon}$ esto se deriva de la definición ${displaystyle F'.}$
• De lo contrario, déjalo ${displaystyle w=va}$ con ${displaystyle vin Sigma}$ y ${displaystyle ain Sigma.}$

Desde ${displaystyle delta '^{*}(q_{0},w)=delta ^{*}(q_{0},w)}$ y ${displaystyle Fsubseteq F',}$ tenemos

$${displaystyle delta '^{*}(q_{0},w)cap F'neq {};Leftarrow ;delta ^{*}(q_{0},w)cap Fneq{};}$$

todavía tenemos que mostrar el "${displaystyle "Rightarrow"$"Dirección.

• Si ${displaystyle delta '^{*}(q_{0},w)}$ contiene un estado en ${displaystyle F'setminus {q_{0}}}$ entonces ${displaystyle delta ^{*}(q_{0},w)}$ contiene el mismo estado, que se encuentra en ${displaystyle F}$.
• Si ${displaystyle delta '^{*}(q_{0},w)}$ contiene ${displaystyle q_{0}$ y ${displaystyle q_{0}in F,}$ entonces ${displaystyle delta ^{*}(q_{0},w)}$ también contiene un estado en ${displaystyle F,}$ viz. ${displaystyle q_{0}$
• Si ${displaystyle delta '^{*}(q_{0},w)}$ contiene ${displaystyle q_{0}$ y ${displaystyle q_{0}not in F,}$ entonces el estado en ${displaystyle E(q_{0}cap F}$ debe estar en ${textstyle delta ^{*}(q_{0},w)=bigcup _{rin delta ^{*}(q,v)}E(delta (r,a)). }$

Dado que NFA es equivalente a DFA, NFA-ε también es equivalente a DFA.

Propiedades de cierre

El conjunto de idiomas reconocidos por las NFA se cierra mediante las siguientes operaciones. Estas operaciones de cierre se utilizan en el algoritmo de construcción de Thompson, que construye un NFA a partir de cualquier expresión regular. También se pueden utilizar para demostrar que las NFA reconocen exactamente los idiomas habituales.

• Unión (cf. cuadro); es decir, si el idioma L₁ es aceptado por algunos NFA A₁ y L₂ por algunos A₂, entonces un NFA A_u se puede construir que acepte el idioma L₁∪L₂.
• Intersección; similarmente, de A₁ y A₂ NFA A_i puede ser construido que acepta L₁∩L₂.
• Concatenación
• Negation; similarly, from A₁ NFA A_n puede ser construido que acepta la^*L₁.
• Cierre de Kleene

Dado que los NFA son equivalentes a autómatas finitos no deterministas con ε-movimientos (NFA-ε), los cierres anteriores se prueban utilizando las propiedades de cierre de NFA-ε.

Propiedades

La máquina arranca en el estado inicial especificado y lee una cadena de símbolos de su alfabeto. El autómata utiliza la función de transición de estado Δ para determinar el siguiente estado utilizando el estado actual y el símbolo recién leído o la cadena vacía. Sin embargo, "el siguiente estado de una NFA depende no sólo del evento de entrada actual, sino también de un número arbitrario de eventos de entrada posteriores". Hasta que ocurran estos eventos posteriores, no es posible determinar en qué estado se encuentra la máquina". Si, cuando el autómata ha terminado de leer, está en estado de aceptación, se dice que la NFA acepta la cadena; en caso contrario, se dice que rechaza la cadena.

El conjunto de todas las cadenas aceptadas por una NFA es el idioma que acepta la NFA. Este idioma es un idioma regular.

Para cada NFA se puede encontrar un autómata finito determinista (DFA) que acepta el mismo lenguaje. Por lo tanto, es posible convertir una NFA existente en una DFA con el fin de implementar una máquina (quizás) más simple. Esto se puede realizar utilizando la construcción del conjunto de potencias, lo que puede conducir a un aumento exponencial en el número de estados necesarios. Para obtener una prueba formal de la construcción de Powerset, consulte el artículo sobre construcción de Powerset.

Implementación

Hay muchas maneras de implementar una NFA:

• Convertirse en el equivalente DFA. En algunos casos esto puede causar soplo exponencial en el número de estados.
• Mantenga una estructura de datos fija de todos los estados en los que el NFA podría estar actualmente. En cuanto al consumo de un símbolo de entrada, une los resultados de la función de transición aplicada a todos los estados actuales para obtener el conjunto de los próximos estados; si se permiten movimientos ε, incluya todos los estados alcanzables por tal movimiento (closure ε). Cada paso requiere al máximo s² computaciones, donde s es el número de estados del NFA. En el consumo del último símbolo de entrada, si uno de los estados actuales es un estado final, la máquina acepta la cadena. Una cuerda de longitud n puede ser procesado en el tiempo O(ns²), y espacio O()s).
• Cree múltiples copias. Para cada uno n la NFA crea hasta n−1 copias de la máquina. Cada uno entrará en un estado separado. Si, al consumir el último símbolo de entrada, al menos una copia del NFA está en el estado de aceptación, el NFA aceptará. (Esto también requiere almacenamiento lineal con respecto al número de estados del NFA, ya que puede haber una máquina para cada estado del NFA).
• Explicitamente propagar fichas a través de la estructura de transición de la NFA y coincidir cuando una señal llega al estado final. Esto a veces es útil cuando el NFA debe codificar un contexto adicional sobre los acontecimientos que desencadenaron la transición. (Para una implementación que utiliza esta técnica para hacer un seguimiento de referencias de objetos tienen un vistazo a Tracematches.)
• Es PSPACE-completo probar, dado un NFA, si es universalSi hay una cuerda que no acepta. Lo mismo es cierto problema de inclusión, es decir, dadas dos NFAs, es el idioma de uno un subconjunto del idioma del otro.

Aplicación de NFA

Las NFA y las DFA son equivalentes en el sentido de que si un idioma es reconocido por una NFA, también lo será por una DFA y viceversa. El establecimiento de dicha equivalencia es importante y útil. Es útil porque construir un NFA para reconocer un idioma determinado es a veces mucho más fácil que construir un DFA para ese idioma. Es importante porque los NFA se pueden utilizar para reducir la complejidad del trabajo matemático necesario para establecer muchas propiedades importantes en la teoría de la computación. Por ejemplo, es mucho más fácil probar las propiedades de cierre de lenguajes regulares utilizando NFA que DFA.