Álgebra lineal

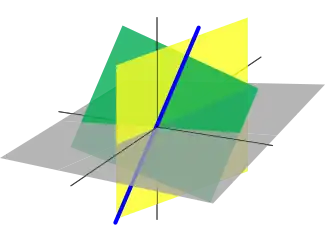
El álgebra lineal es la rama de las matemáticas que se ocupa de las ecuaciones lineales como:

mapas lineales tales como:

y sus representaciones en espacios vectoriales ya través de matrices.

El álgebra lineal es fundamental para casi todas las áreas de las matemáticas. Por ejemplo, el álgebra lineal es fundamental en las presentaciones modernas de geometría, incluso para definir objetos básicos como líneas, planos y rotaciones. Además, el análisis funcional, una rama del análisis matemático, puede verse como la aplicación del álgebra lineal a espacios de funciones.

El álgebra lineal también se usa en la mayoría de las ciencias y campos de la ingeniería, porque permite modelar muchos fenómenos naturales y calcular de manera eficiente con dichos modelos. Para los sistemas no lineales, que no se pueden modelar con álgebra lineal, a menudo se usa para tratar con aproximaciones de primer orden, utilizando el hecho de que el diferencial de una función multivariada en un punto es el mapa lineal que mejor se aproxima a la función cerca de ese punto.

Historia

El procedimiento (usando varillas de conteo) para resolver ecuaciones lineales simultáneas ahora llamado eliminación gaussiana aparece en el antiguo texto matemático chino Capítulo Ocho: Arreglos Rectangulares de Los Nueve Capítulos sobre el Arte Matemático. Su uso se ilustra en dieciocho problemas, con dos a cinco ecuaciones.

Los sistemas de ecuaciones lineales surgieron en Europa con la introducción en 1637 por René Descartes de coordenadas en geometría. De hecho, en esta nueva geometría, ahora llamada geometría cartesiana, las líneas y los planos están representados por ecuaciones lineales, y calcular sus intersecciones equivale a resolver sistemas de ecuaciones lineales.

Los primeros métodos sistemáticos para resolver sistemas lineales usaban determinantes, considerados por primera vez por Leibniz en 1693. En 1750, Gabriel Cramer los usó para dar soluciones explícitas de sistemas lineales, ahora llamada regla de Cramer. Más tarde, Gauss describió con más detalle el método de eliminación, que inicialmente se catalogó como un avance en la geodesia.

En 1844, Hermann Grassmann publicó su "Teoría de la extensión", que incluía nuevos temas fundamentales de lo que hoy se llama álgebra lineal. En 1848, James Joseph Sylvester introdujo el término matriz, que en latín significa matriz.

El álgebra lineal creció con ideas anotadas en el plano complejo. Por ejemplo, dos números w y z en ℂ tienen una diferencia w – z, y los segmentos de recta wz y 0(w − z) tienen la misma longitud y dirección. Los segmentos son equipolentes. El sistema de cuatro dimensiones ℍ de cuaterniones se inició en 1843. El término vector se introdujo como v = x i + y j + z k representando un punto en el espacio. La diferencia de cuaterniones p– q también produce un segmento equipolento a pq. Otros sistemas numéricos hipercomplejos también utilizaron la idea de un espacio lineal con una base.

Arthur Cayley introdujo la multiplicación de matrices y la matriz inversa en 1856, haciendo posible el grupo lineal general. El mecanismo de representación de grupos se volvió disponible para describir números complejos e hipercomplejos. De manera crucial, Cayley usó una sola letra para denotar una matriz, tratando así a una matriz como un objeto agregado. También se dio cuenta de la conexión entre matrices y determinantes, y escribió: "Habría muchas cosas que decir sobre esta teoría de matrices que, me parece, debería preceder a la teoría de determinantes".

Benjamin Peirce publicó su Álgebra asociativa lineal (1872), y su hijo Charles Sanders Peirce amplió el trabajo más tarde.

El telégrafo requería un sistema explicativo, y la publicación de 1873 de A Treatise on Electricity and Magnetism instituyó una teoría de campo de fuerzas y requirió geometría diferencial para su expresión. El álgebra lineal es geometría diferencial plana y sirve en espacios tangentes a variedades. Las simetrías electromagnéticas del espacio-tiempo se expresan mediante las transformaciones de Lorentz, y gran parte de la historia del álgebra lineal es la historia de las transformaciones de Lorentz.

Peano introdujo la primera definición moderna y más precisa de un espacio vectorial en 1888; en 1900, había surgido una teoría de transformaciones lineales de espacios vectoriales de dimensión finita. El álgebra lineal tomó su forma moderna en la primera mitad del siglo XX, cuando muchas ideas y métodos de siglos anteriores se generalizaron como álgebra abstracta. El desarrollo de las computadoras condujo a una mayor investigación en algoritmos eficientes para la eliminación de Gauss y la descomposición de matrices, y el álgebra lineal se convirtió en una herramienta esencial para el modelado y las simulaciones.

Espacios vectoriales

Hasta el siglo XIX, el álgebra lineal se introdujo a través de sistemas de ecuaciones y matrices lineales. En las matemáticas modernas, generalmente se prefiere la presentación a través de espacios vectoriales, ya que es más sintética, más general (no limitada al caso de dimensión finita) y conceptualmente más simple, aunque más abstracta.

Un espacio vectorial sobre un campo F (a menudo el campo de los números reales) es un conjunto V equipado con dos operaciones binarias que satisfacen los siguientes axiomas. Los elementos de V se llaman vectores y los elementos de F se llaman escalares. La primera operación, la suma de vectores, toma dos vectores v y w y genera un tercer vector v + w. La segunda operación, multiplicación escalar, toma cualquier escalar a y cualquier vector v y genera un nuevo vector a v. Los axiomas que deben satisfacer la suma y la multiplicación escalar son los siguientes. (En la lista a continuación, u, v y w son elementos arbitrarios de V, y a y b son escalares arbitrarios en el campo F).

Axioma	Significación
Asociatividad de la suma	tu + (v + w) = (tu + v) + w
Conmutatividad de la suma	tu + v = v + tu
Elemento de identidad de la suma	Existe un elemento 0 en V, llamado vector cero (o simplemente cero), tal que v + 0 = v para todo v en V.
Elementos inversos de la suma	Para cada v en V, existe un elemento − v en V, llamado inverso aditivo de v, tal que v + (− v) = 0
Distributividad de la multiplicación escalar con respecto a la suma vectorial	una (tu + v) = una tu + una v
Distributividad de la multiplicación escalar con respecto a la suma de campos	(un + segundo) v = un v + segundo v
Compatibilidad de la multiplicación escalar con la multiplicación de campo	un (segundo v) = (ab) v
Elemento de identidad de la multiplicación escalar	1 v = v, donde 1 denota la identidad multiplicativa de F.

Los primeros cuatro axiomas significan que V es un grupo abeliano bajo suma.

Un elemento de un espacio vectorial específico puede tener varias naturalezas; por ejemplo, podría ser una sucesión, una función, un polinomio o una matriz. El álgebra lineal se ocupa de aquellas propiedades de tales objetos que son comunes a todos los espacios vectoriales.

Mapas lineales

Los mapas lineales son mapeos entre espacios vectoriales que conservan la estructura del espacio vectorial. Dados dos espacios vectoriales V y W sobre un campo F, un mapa lineal (también llamado, en algunos contextos, transformación lineal o mapeo lineal) es un mapa

que es compatible con la suma y la multiplicación escalar, es decir

para cualquier vector u, v en V y escalar a en F.

Esto implica que para cualesquiera vectores u, v en V y escalares a, b en F, se tiene

Cuando V = W son el mismo espacio vectorial, un mapa lineal T: V → V también se conoce como operador lineal en V.

Un mapa lineal biyectivo entre dos espacios vectoriales (es decir, cada vector del segundo espacio está asociado con exactamente uno en el primero) es un isomorfismo. Debido a que un isomorfismo conserva la estructura lineal, dos espacios vectoriales isomorfos son "esencialmente iguales" desde el punto de vista del álgebra lineal, en el sentido de que no se pueden distinguir mediante el uso de propiedades de espacio vectorial. Una cuestión esencial en álgebra lineal es probar si una aplicación lineal es un isomorfismo o no y, si no lo es, encontrar su rango (o imagen) y el conjunto de elementos que se asignan al vector cero, llamado kernel. del mapa Todas estas preguntas se pueden resolver utilizando la eliminación gaussiana o alguna variante de este algoritmo.

Subespacios, intervalo y base

El estudio de aquellos subconjuntos de espacios vectoriales que son en sí mismos espacios vectoriales bajo las operaciones inducidas es fundamental, al igual que para muchas estructuras matemáticas. Estos subconjuntos se denominan subespacios lineales. Más precisamente, un subespacio lineal de un espacio vectorial V sobre un campo F es un subconjunto W de V tal que u + v y a u están en W, para cada u, v en W y cada a en F. (Estas condiciones son suficientes para implicar que W es un espacio vectorial).

Por ejemplo, dado un mapa lineal T: V → W, la imagen T (V) de V, y la imagen inversa T (0) de 0 (llamada núcleo o espacio nulo), son subespacios lineales de W y V, respectivamente.

Otra forma importante de formar un subespacio es considerar combinaciones lineales de un conjunto S de vectores: el conjunto de todas las sumas

donde v ₁, v ₂,..., v _k están en S, y a ₁, a ₂,..., a _k están en F forman un subespacio lineal llamado lapso de S. El lapso de S es también la intersección de todos los subespacios lineales que contienen S. En otras palabras, es el subespacio lineal más pequeño (para la relación de inclusión) que contiene S.

Un conjunto de vectores es linealmente independiente si ninguno está en el lapso de los demás. De manera equivalente, un conjunto S de vectores es linealmente independiente si la única forma de expresar el vector cero como una combinación lineal de elementos de S es tomar cero para cada coeficiente a _i.

Un conjunto de vectores que genera un espacio vectorial se denomina conjunto generador o conjunto generador. Si un conjunto generador S es linealmente dependiente (que no es linealmente independiente), entonces algún elemento w de S está en el intervalo de los otros elementos de S, y el intervalo seguiría siendo el mismo si se elimina w de S. Uno puede continuar eliminando elementos de S hasta obtener un conjunto generador linealmente independiente. Tal conjunto linealmente independiente que genera un espacio vectorial V se llama base de V. La importancia de las bases radica en que son simultáneamente conjuntos generadores mínimos y conjuntos independientes máximos. Más precisamente, si S es un conjunto linealmente independiente y T es un conjunto generador tal que S ⊆ T, entonces existe una base B tal que S ⊆ B ⊆ T.

Dos bases cualesquiera de un espacio vectorial V tienen la misma cardinalidad, lo que se denomina dimensión de V; este es el teorema de la dimensión para espacios vectoriales. Además, dos espacios vectoriales sobre el mismo campo F son isomorfos si y solo si tienen la misma dimensión.

Si cualquier base de V (y por tanto toda base) tiene un número finito de elementos, V es un espacio vectorial de dimensión finita. Si U es un subespacio de V, entonces dim U ≤ dim V. En el caso de que V sea de dimensión finita, la igualdad de las dimensiones implica U = V.

Si U ₁ y U ₂ son subespacios de V, entonces

donde U ₁ + U ₂ denota el lapso de U ₁ ∪ U ₂.

Matrices

Las matrices permiten la manipulación explícita de espacios vectoriales de dimensión finita y mapas lineales. Su teoría es, por lo tanto, una parte esencial del álgebra lineal.

Sea V un espacio vectorial de dimensión finita sobre un campo F, y (v ₁, v ₂,..., v _m) una base de V (así m es la dimensión de V). Por definición de una base, el mapa

es una biyección de F, el conjunto de las sucesiones de m elementos de F, sobre V. Este es un isomorfismo de espacios vectoriales, si F está equipado con su estructura estándar de espacio vectorial, donde la suma vectorial y la multiplicación escalar se realizan componente por componente.

Este isomorfismo permite representar un vector por su imagen inversa bajo este isomorfismo, es decir por el vector de coordenadas (a ₁,..., a _m) o por la matriz columna

Si W es otro espacio vectorial de dimensión finita (posiblemente el mismo), con una base (w ₁,..., w _n), un mapa lineal f de W a V está bien definido por sus valores en los elementos base, es decir (f (w ₁),..., f (w _n)). Por lo tanto, f está bien representada por la lista de matrices de columnas correspondientes. es decir, si

para j = 1,..., n, entonces f está representada por la matriz

con m filas y n columnas.

La multiplicación de matrices se define de tal forma que el producto de dos matrices es la matriz de la composición de las correspondientes funciones lineales, y el producto de una matriz por una matriz columna es la matriz columna que representa el resultado de aplicar la función lineal representada a el vector representado. De ello se deduce que la teoría de los espacios vectoriales de dimensión finita y la teoría de las matrices son dos lenguajes diferentes para expresar exactamente los mismos conceptos.

Dos matrices que codifican la misma transformación lineal en diferentes bases se llaman similares. Se puede demostrar que dos matrices son semejantes si y sólo si una puede transformarse una en la otra mediante operaciones elementales de fila y columna. Para una matriz que representa un mapa lineal de W a V, las operaciones de fila corresponden al cambio de bases en V y las operaciones de columna corresponden al cambio de bases en W. Cada matriz es similar a una matriz de identidad posiblemente bordeada por cero filas y cero columnas. En términos de espacios vectoriales, esto significa que, para cualquier aplicación lineal de W a V, hay bases tales que una parte de la base de Wse asigna biyectivamente en una parte de la base de V, y que los elementos básicos restantes de W, si los hay, se asignan a cero. La eliminación gaussiana es el algoritmo básico para encontrar estas operaciones elementales y probar estos resultados.

Sistemas lineales

Un conjunto finito de ecuaciones lineales en un conjunto finito de variables, por ejemplo, x ₁, x ₂,..., x _n, o x, y,..., z se denomina sistema de ecuaciones lineales o sistema lineal.

Los sistemas de ecuaciones lineales forman parte fundamental del álgebra lineal. Históricamente, el álgebra lineal y la teoría de matrices se han desarrollado para resolver tales sistemas. En la presentación moderna del álgebra lineal a través de espacios vectoriales y matrices, muchos problemas pueden interpretarse en términos de sistemas lineales.

Por ejemplo, deja

(S)

ser un sistema lineal.

A tal sistema, uno puede asociar su matriz

y su vector miembro derecho

Sea T la transformación lineal asociada a la matriz M. Una solución del sistema (S) es un vector

tal que

que es un elemento de la preimagen de v por T.

Sea (S′) el sistema homogéneo asociado, donde los lados derechos de las ecuaciones se anulan:

(S′)

Las soluciones de (S′) son exactamente los elementos del núcleo de T o, de manera equivalente, M.

La eliminación gaussiana consiste en realizar operaciones de fila elementales en la matriz aumentada

para ponerlo en forma escalonada de filas reducidas. Estas operaciones de fila no cambian el conjunto de soluciones del sistema de ecuaciones. En el ejemplo, la forma escalonada reducida es

mostrando que el sistema (S) tiene solución única

De esta interpretación matricial de los sistemas lineales se deduce que se pueden aplicar los mismos métodos para resolver sistemas lineales y para muchas operaciones sobre matrices y transformaciones lineales, que incluyen el cálculo de rangos, núcleos, matrices inversas.

Endomorfismos y matrices cuadradas

Un endomorfismo lineal es un mapa lineal que mapea un espacio vectorial V a sí mismo. Si V tiene una base de n elementos, dicho endomorfismo se representa mediante una matriz cuadrada de tamaño n.

Con respecto a los mapas lineales generales, los endomorfismos lineales y las matrices cuadradas tienen algunas propiedades específicas que hacen que su estudio sea una parte importante del álgebra lineal, que se usa en muchas partes de las matemáticas, incluidas las transformaciones geométricas, los cambios de coordenadas, las formas cuadráticas y muchas otras partes. de las matemáticas

Determinante

El determinante de una matriz cuadrada A se define como

donde S _n es el grupo de todas las permutaciones de n elementos, σ es una permutación y (−1) la paridad de la permutación. Una matriz es invertible si y sólo si el determinante es invertible (es decir, distinto de cero si los escalares pertenecen a un campo).

La regla de Cramer es una expresión de forma cerrada, en términos de determinantes, de la solución de un sistema de n ecuaciones lineales en n incógnitas. La regla de Cramer es útil para razonar sobre la solución, pero, a excepción de n = 2 o 3, rara vez se usa para calcular una solución, ya que la eliminación gaussiana es un algoritmo más rápido.

El determinante de un endomorfismo es el determinante de la matriz que representa el endomorfismo en términos de alguna base ordenada. Esta definición tiene sentido, ya que este determinante es independiente de la elección de la base.

Valores propios y vectores propios

Si f es un endomorfismo lineal de un espacio vectorial V sobre un campo F, un vector propio de f es un vector v distinto de cero de V tal que f (v) = av para algún escalar a en F. Este escalar a es un valor propio de f.

Si la dimensión de V es finita y se ha elegido una base, fyv pueden representarse, respectivamente, por una matriz cuadrada M y una matriz columna z; la ecuación que define los vectores propios y los valores propios se convierte en

Usando la matriz identidad I, cuyas entradas son todas cero, excepto las de la diagonal principal, que son iguales a uno, esto se puede reescribir

Como se supone que z es distinto de cero, esto significa que M – aI es una matriz singular y, por lo tanto, su determinante det (M − aI) es igual a cero. Los valores propios son, por lo tanto, las raíces del polinomio

Si V es de dimensión n, se trata de un polinomio mónico de grado n, llamado polinomio característico de la matriz (o del endomorfismo), y existen, como máximo, n autovalores.

Si existe una base que consta solo de vectores propios, la matriz de f sobre esta base tiene una estructura muy simple: es una matriz diagonal tal que las entradas en la diagonal principal son valores propios y las otras entradas son cero. En este caso, se dice que el endomorfismo y la matriz son diagonalizables. De manera más general, un endomorfismo y una matriz también se dicen diagonalizables, si se vuelven diagonalizables después de extender el campo de escalares. En este sentido extendido, si el polinomio característico no tiene cuadrados, entonces la matriz es diagonalizable.

Una matriz simétrica siempre es diagonalizable. Hay matrices no diagonalizables, siendo la más simple

(no puede ser diagonalizable ya que su cuadrado es la matriz cero, y el cuadrado de una matriz diagonal distinta de cero nunca es cero).

Cuando un endomorfismo no es diagonalizable, hay bases en las que tiene una forma simple, aunque no tan simple como la forma diagonal. La forma normal de Frobenius no necesita extender el campo de los escalares y hace que el polinomio característico sea inmediatamente legible en la matriz. La forma normal de Jordan requiere extender el campo del escalar para contener todos los valores propios, y se diferencia de la forma diagonal solo por algunas entradas que están justo encima de la diagonal principal y son iguales a 1.

Dualidad

Una forma lineal es un mapa lineal de un espacio vectorial V sobre un campo F al campo de escalares F, visto como un espacio vectorial sobre sí mismo. Equipadas con la suma puntual y la multiplicación por un escalar, las formas lineales forman un espacio vectorial, llamado espacio dual de V, y generalmente denotado V* o V′.

Si v ₁,..., v _n es una base de V (esto implica que V es de dimensión finita), entonces se puede definir, para i = 1,..., n, una aplicación lineal v _i * tal que v _yo *(v _yo) = 1 y v _yo *(v _j) = 0 si j ≠ yo. Estos mapas lineales forman una base de V *, llamada base dual de v ₁,..., v _n. (SiV no es de dimensión finita, el v _i * puede definirse de manera similar; son linealmente independientes, pero no forman una base.)

Para v en V, el mapa

es una forma lineal en V*. Esto define el mapa lineal canónico de V en (V *)*, el dual de V*, llamado bidual de V. Esta aplicación canónica es un isomorfismo si V es de dimensión finita, y esto permite identificar a V con su bidual. (En el caso de dimensión infinita, el mapa canónico es inyectivo, pero no sobreyectivo).

Por lo tanto, existe una simetría completa entre un espacio vectorial de dimensión finita y su dual. Esto motiva el uso frecuente, en este contexto, de la notación bra-ket

para denotar f (x).

Mapa doble

Dejar

Sea un mapa lineal. Para cada forma lineal h en W, la función compuesta h ∘ f es una forma lineal en V. Esto define un mapa lineal

entre los espacios duales, que se llama el dual o la transposición de f.

Si V y W son de dimensión finita, y M es la matriz de f en términos de algunas bases ordenadas, entonces la matriz de f * sobre las bases duales es la transpuesta M de M, obtenida intercambiando filas y columnas.

Si los elementos de espacios vectoriales y sus duales están representados por vectores columna, esta dualidad puede expresarse en notación corchete por

Para resaltar esta simetría, los dos miembros de esta igualdad a veces se escriben

Espacios de productos internos

Además de estos conceptos básicos, el álgebra lineal también estudia espacios vectoriales con estructura adicional, como un producto interno. El producto interno es un ejemplo de una forma bilineal y le da al espacio vectorial una estructura geométrica al permitir la definición de longitud y ángulos. Formalmente, un producto interno es un mapa

que satisface los siguientes tres axiomas para todos los vectores u, v, w en V y todos los escalares a en F:

• Simetría conjugada:

En ℝ, es simétrico.

• Linealidad en el primer argumento:
• Definición positiva:

con igualdad solo para v = 0.

Podemos definir la longitud de un vector v en V por

y podemos demostrar la desigualdad de Cauchy-Schwarz:

En particular, la cantidad

y así podemos llamar a esta cantidad el coseno del ángulo entre los dos vectores.

Dos vectores son ortogonales si ⟨ u, v ⟩ = 0. Una base ortonormal es una base en la que todos los vectores base tienen una longitud de 1 y son ortogonales entre sí. Dado cualquier espacio vectorial de dimensión finita, se podría encontrar una base ortonormal mediante el procedimiento de Gram-Schmidt. Las bases ortonormales son particularmente fáciles de manejar, ya que si v = a ₁ v ₁ + ⋯ + a _n v _n, entonces

El producto interior facilita la construcción de muchos conceptos útiles. Por ejemplo, dada una transformada T, podemos definir su conjugado hermitiano T* como la transformada lineal que satisface

Si T satisface TT* = T*T, llamamos a T normal. Resulta que las matrices normales son precisamente las matrices que tienen un sistema ortonormal de vectores propios que generan V.

Relación con la geometría

Existe una fuerte relación entre el álgebra lineal y la geometría, que comenzó con la introducción por parte de René Descartes, en 1637, de las coordenadas cartesianas. En esta nueva geometría (en ese momento), ahora llamada geometría cartesiana, los puntos se representan mediante coordenadas cartesianas, que son secuencias de tres números reales (en el caso del espacio tridimensional habitual). Los objetos básicos de la geometría, que son líneas y planos, están representados por ecuaciones lineales. Por lo tanto, calcular las intersecciones de líneas y planos equivale a resolver sistemas de ecuaciones lineales. Esta fue una de las principales motivaciones para desarrollar el álgebra lineal.

La mayoría de las transformaciones geométricas, como traslaciones, rotaciones, reflejos, movimientos rígidos, isometrías y proyecciones transforman líneas en líneas. De ello se deduce que pueden definirse, especificarse y estudiarse en términos de mapas lineales. Este es también el caso de las homografías y las transformaciones de Möbius, cuando se las considera como transformaciones de un espacio proyectivo.

Hasta finales del siglo XIX, los espacios geométricos estaban definidos por axiomas que relacionaban puntos, líneas y planos (geometría sintética). Alrededor de esta fecha, parecía que también se pueden definir espacios geométricos mediante construcciones que involucran espacios vectoriales (ver, por ejemplo, Espacio proyectivo y Espacio afín). Se ha demostrado que los dos enfoques son esencialmente equivalentes. En geometría clásica, los espacios vectoriales involucrados son espacios vectoriales sobre los reales, pero las construcciones pueden extenderse a espacios vectoriales sobre cualquier campo, permitiendo considerar la geometría sobre campos arbitrarios, incluyendo campos finitos.

En la actualidad, la mayoría de los libros de texto introducen espacios geométricos a partir del álgebra lineal y, a menudo, la geometría se presenta, a nivel elemental, como un subcampo del álgebra lineal.

Uso y aplicaciones

El álgebra lineal se usa en casi todas las áreas de las matemáticas, por lo que es relevante en casi todos los dominios científicos que usan matemáticas. Estas aplicaciones se pueden dividir en varias categorías amplias.

Geometría del espacio ambiental.

El modelado del espacio ambiental se basa en la geometría. Las ciencias que se ocupan de este espacio utilizan ampliamente la geometría. Este es el caso de la mecánica y la robótica, para describir la dinámica de los cuerpos rígidos; geodesia para describir la forma de la Tierra; perspectiva, visión por computadora y gráficos por computadora, para describir la relación entre una escena y su representación plana; y muchos otros dominios científicos.

En todas estas aplicaciones, la geometría sintética se usa a menudo para descripciones generales y un enfoque cualitativo, pero para el estudio de situaciones explícitas, se debe calcular con coordenadas. Esto requiere el uso intensivo del álgebra lineal.

Análisis funcional

El análisis funcional estudia los espacios de funciones. Estos son espacios vectoriales con estructura adicional, como los espacios de Hilbert. El álgebra lineal es así una parte fundamental del análisis funcional y sus aplicaciones, que incluyen, en particular, la mecánica cuántica (funciones de onda).

Estudio de sistemas complejos

La mayoría de los fenómenos físicos se modelan mediante ecuaciones diferenciales parciales. Para resolverlos, se suele descomponer el espacio en el que se buscan las soluciones en pequeñas celdas que interactúan entre sí. Para los sistemas lineales, esta interacción implica funciones lineales. Para sistemas no lineales, esta interacción a menudo se aproxima mediante funciones lineales. En ambos casos, generalmente están involucradas matrices muy grandes. El pronóstico del tiempo es un ejemplo típico, donde toda la atmósfera terrestre se divide en celdas de, digamos, 100 km de ancho y 100 m de alto.

Cálculo científico

Casi todos los cálculos científicos implican álgebra lineal. En consecuencia, los algoritmos de álgebra lineal han sido altamente optimizados. BLAS y LAPACK son las implementaciones más conocidas. Para mejorar la eficiencia, algunos de ellos configuran los algoritmos automáticamente, en tiempo de ejecución, para adaptarlos a las especificidades de la computadora (tamaño de caché, número de núcleos disponibles,...).

Algunos procesadores, generalmente unidades de procesamiento de gráficos (GPU), están diseñados con una estructura matricial para optimizar las operaciones de álgebra lineal.

Extensiones y generalizaciones

Esta sección presenta varios temas relacionados que generalmente no aparecen en los libros de texto elementales sobre álgebra lineal, pero que comúnmente se consideran, en matemáticas avanzadas, como partes del álgebra lineal.

Teoría del módulo

La existencia de inversos multiplicativos en campos no está involucrada en los axiomas que definen un espacio vectorial. Uno puede entonces reemplazar el campo de escalares por un anillo R, y esto da una estructura llamada módulo sobre R, o R - módulo.

Los conceptos de independencia lineal, amplitud, base y aplicaciones lineales (también llamados homomorfismos de módulo) se definen para los módulos exactamente como para los espacios vectoriales, con la diferencia esencial de que, si R no es un campo, hay módulos que no tienen ningún base. Los módulos que tienen una base son los módulos libres y los que están atravesados ​​por un conjunto finito son los módulos generados finitamente. Los homomorfismos de módulos entre módulos libres generados finitamente pueden representarse mediante matrices. La teoría de las matrices sobre un anillo es similar a la de las matrices sobre un campo, excepto que los determinantes existen solo si el anillo es conmutativo, y que una matriz cuadrada sobre un anillo conmutativo es invertible solo si su determinante tiene un inverso multiplicativo en el anillo..

Los espacios vectoriales se caracterizan completamente por su dimensión (hasta un isomorfismo). En general, no existe una clasificación tan completa para los módulos, incluso si uno se restringe a módulos generados finitamente. Sin embargo, cada módulo es un cokernel de un homomorfismo de módulos libres.

Los módulos sobre los números enteros se pueden identificar con grupos abelianos, ya que la multiplicación por un número entero se puede identificar con una suma repetida. La mayor parte de la teoría de grupos abelianos puede extenderse a módulos sobre un dominio ideal principal. En particular, sobre un dominio ideal principal, cada submódulo de un módulo libre es libre, y el teorema fundamental de los grupos abelianos finitamente generados puede extenderse directamente a módulos finitamente generados sobre un anillo principal.

Hay muchos anillos para los que existen algoritmos para resolver ecuaciones lineales y sistemas de ecuaciones lineales. Sin embargo, estos algoritmos tienen generalmente una complejidad computacional mucho mayor que los algoritmos similares sobre un campo. Para obtener más detalles, consulte Ecuación lineal sobre un anillo.

Álgebra multilineal y tensores

En álgebra multilineal, se consideran transformaciones lineales multivariables, es decir, aplicaciones que son lineales en cada una de varias variables diferentes. Esta línea de investigación conduce naturalmente a la idea del espacio dual, el espacio vectorial V* que consta de mapas lineales f: V → F donde F es el campo de escalares. Los mapas multilineales T: V → F se pueden describir mediante productos tensoriales de elementos de V*.

Si, además de la suma vectorial y la multiplicación escalar, existe un producto vectorial bilineal V × V → V, el espacio vectorial se denomina álgebra; por ejemplo, las álgebras asociativas son álgebras con un producto vectorial asociado (como el álgebra de matrices cuadradas o el álgebra de polinomios).

Espacios vectoriales topológicos

Los espacios vectoriales que no son de dimensión finita a menudo requieren una estructura adicional para ser manejables. Un espacio vectorial normado es un espacio vectorial junto con una función llamada norma, que mide el "tamaño" de los elementos. La norma induce una métrica, que mide la distancia entre elementos, e induce una topología, que permite definir mapas continuos. La métrica también permite una definición de límites y completitud: un espacio métrico que está completo se conoce como espacio de Banach. Un espacio métrico completo junto con la estructura adicional de un producto interno (una forma sesquilineal simétrica conjugada) se conoce como espacio de Hilbert, que en cierto sentido es un espacio de Banach particularmente bueno. El análisis funcional aplica los métodos del álgebra lineal junto con los del análisis matemático para estudiar varios espacios de funciones;Espacios L, que son espacios de Banach, y especialmente el espacio L de funciones cuadradas integrables, que es el único espacio de Hilbert entre ellos. El análisis funcional es de particular importancia para la mecánica cuántica, la teoría de las ecuaciones diferenciales parciales, el procesamiento de señales digitales y la ingeniería eléctrica. También proporciona la base y el marco teórico que subyace a la transformada de Fourier y métodos relacionados.

Álgebra homológica