Álgebra homológica

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

El álgebra homológica es la rama de las matemáticas que estudia la homología en un entorno algebraico general. Es una disciplina relativamente joven, cuyos orígenes se remontan a las investigaciones en topología combinatoria (precursora de la topología algebraica) y álgebra abstracta (teoría de módulos y sicigias) a finales del siglo XIX, principalmente por Henri Poincaré y David Hilbert.

El desarrollo del álgebra homológica estuvo estrechamente relacionado con el surgimiento de la teoría de categorías. En general, el álgebra homológica es el estudio de los funtores homológicos y las intrincadas estructuras algebraicas que implican. Un concepto bastante útil y omnipresente en matemáticas es el de complejos de cadenas, que se pueden estudiar tanto a través de su homología como de su cohomología. El álgebra homológica proporciona los medios para extraer la información contenida en estos complejos y presentarla en forma de invariantes homológicos de anillos, módulos, espacios topológicos y otros objetos matemáticos "tangibles". Las secuencias espectrales proporcionan una poderosa herramienta para hacer esto.

Desde sus orígenes, el álgebra homológica ha jugado un papel enorme en la topología algebraica. Su influencia se ha expandido gradualmente y actualmente incluye álgebra conmutativa, geometría algebraica, teoría de números algebraicos, teoría de representación, física matemática, álgebras de operadores, análisis complejo y la teoría de ecuaciones diferenciales parciales. La teoría K es una disciplina independiente que se basa en métodos del álgebra homológica, al igual que la geometría no conmutativa de Alain Connes.

Historia del álgebra homológica

El álgebra homológica comenzó a estudiarse en su forma más básica en la década de 1800 como una rama de la topología, pero no fue hasta la década de 1940 que se convirtió en una materia independiente con el estudio de objetos como el funtor ext y el funtor tor, entre otros. otros.

Complejos de cadena y homología.

La noción de cadena compleja es central en el álgebra homológica. Un complejo de cadena abstracto es una secuencia $(C_bullet, d_bullet)$ de grupos abelianos y homomorfismos de grupo, con la propiedad de que la composición de dos mapas consecutivos cualesquiera es cero: $C_bullet: cdots longrightarrow C_{n+1} stackrel{d_{n+1}}{longrightarrow} C_n stackrel{d_n}{longrightarrow} C_{n-1} stackrel{d_{n -1}}{longrightarrow} cdots, quad d_n circ d_{n+1}=0.$

Los elementos de C _n se denominan cadenas n y los homomorfismos d _n se denominan mapas de contorno o diferenciales. Los grupos de cadena Cn pueden estar _dotados de una estructura adicional; por ejemplo, pueden ser espacios vectoriales o módulos sobre un anillo fijo R. Los diferenciales deben preservar la estructura extra si existe; por ejemplo, deben ser mapas lineales u homomorfismos de módulos R. Por conveniencia notacional, restrinja la atención a los grupos abelianos (más correctamente, a la categoría Ab de grupos abelianos); un célebre teorema de Barry Mitchell implica que los resultados se generalizarán a cualquier categoría abeliana. Cada cadena compleja define dos secuencias adicionales de grupos abelianos, los ciclos Z _n = Ker d _n y los límites B _n = Im d _{n +1}, donde Ker d e Im d denotan el núcleo y la imagen de d. Dado que la composición de dos mapas de límites consecutivos es cero, estos grupos están incrustados entre sí como $B_n subconjunto Z_n subconjunto C_n.$

Los subgrupos de grupos abelianos son automáticamente normales; por lo tanto, podemos definir el n -ésimo grupo de homología H _n (C) como el grupo de factores de los n -ciclos por los n -límites, $H_n(C) = Z_n/B_n = operatorname{Ker}, d_n/ operatorname{Im}, d_{n+1}.$

Un complejo de cadena se llama acíclico o una secuencia exacta si todos sus grupos de homología son cero.

Los complejos de cadenas surgen en abundancia en álgebra y topología algebraica. Por ejemplo, si X es un espacio topológico, entonces las cadenas singulares C _n (X) son combinaciones lineales formales de aplicaciones continuas desde el estándar n -simple hasta X; si K es un complejo simplicial entonces las cadenas simpliciales C _n (K) son combinaciones lineales formales de los n -simples de K; si A = F / R es una presentación de un grupo abeliano A por generadores y relaciones, donde Fes un grupo abeliano libre generado por los generadores y R es el subgrupo de relaciones, entonces haciendo que C ₁ (A) = R, C ₀ (A) = F, y C _n (A) = 0 para todos los demás n define una secuencia de grupos abelianos. En todos estos casos, existen diferenciales naturales d _n que hacen de C _n un complejo en cadena, cuya homología refleja la estructura del espacio topológico X, el complejo simplicial K, o el grupo abeliano A. En el caso de los espacios topológicos, llegamos a la noción de homología singular, que juega un papel fundamental en la investigación de las propiedades de tales espacios, por ejemplo, las variedades.

A nivel filosófico, el álgebra homológica nos enseña que ciertos complejos en cadena asociados con objetos algebraicos o geométricos (espacios topológicos, complejos simpliciales, módulos R) contienen mucha información algebraica valiosa sobre ellos, siendo la homología solo la parte más fácilmente disponible.. A nivel técnico, el álgebra homológica proporciona las herramientas para manipular complejos y extraer esta información. Aquí hay dos ilustraciones generales.

Dos objetos X e Y están conectados por un mapa f entre ellos. El álgebra homológica estudia la relación, inducida por el mapa f, entre cadenas complejas asociadas a X e Y y su homología. Esto se generaliza al caso de varios objetos y mapas que los conectan. Expresado en el lenguaje de la teoría de categorías, el álgebra homológica estudia las propiedades funcionales de varias construcciones de cadenas complejas y de la homología de estos complejos.
Un objeto X admite múltiples descripciones (por ejemplo, como un espacio topológico y como un complejo simplicial) o el complejo $C_bullet(X)$ se construye utilizando alguna 'presentación' de X, lo que implica elecciones no canónicas. Es importante conocer el efecto del cambio en la descripción de X en los complejos de cadena asociados con X. Típicamente, el complejo y su homología $H_bullet(C)$ son funcionales con respecto a la presentación; y la homología (aunque no el complejo en sí) es en realidad independiente de la presentación elegida, por lo que es una invariante de X.

Herramientas estándar

Secuencias exactas

En el contexto de la teoría de grupos, una secuencia $G_{0};{xrightarrow {f_{1}}};G_{1};{xrightarrow {f_{2}}};G_{2};{xrightarrow {f_{3} }};cdots ;{xrightarrow {f_{n}}};G_{n}$

de grupos y homomorfismos de grupos se llama exacta si la imagen de cada homomorfismo es igual al núcleo del siguiente: $mathrm{im}(f_k) = mathrm{ker}(f_{k+1}).!$

Tenga en cuenta que la secuencia de grupos y homomorfismos puede ser finita o infinita.

Se puede hacer una definición similar para ciertas otras estructuras algebraicas. Por ejemplo, se podría tener una secuencia exacta de espacios vectoriales y aplicaciones lineales, o de módulos y homomorfismos de módulos. De manera más general, la noción de secuencia exacta tiene sentido en cualquier categoría con núcleos y conúcleos.

Secuencia exacta corta

El tipo más común de sucesión exacta es la sucesión exacta corta. Esta es una secuencia exacta de la forma $A;{overset {f}{hookrightarrow }};B;{overset {g}{twoheadrightarrow }};C$

donde f es un monomorfismo y g es un epimorfismo. En este caso, A es un subobjeto de B, y el cociente correspondiente es isomorfo a C: $C cong B/f(A).$

(donde f(A) = im(f)).

Una sucesión exacta corta de grupos abelianos también se puede escribir como una sucesión exacta con cinco términos: $0;{xrightarrow {}};A;{xrightarrow {f}};B;{xrightarrow {g}};C;{xrightarrow {}};0$

donde 0 representa el objeto cero, como el grupo trivial o un espacio vectorial de dimensión cero. La ubicación de los 0 obliga a ƒ a ser un monomorfismo ya g a ser un epimorfismo (ver más abajo).

Sucesión exacta larga

Una sucesión exacta larga es una sucesión exacta indexada por los números naturales.

Los cinco lemas

Considere el siguiente diagrama conmutativo en cualquier categoría abeliana (como la categoría de grupos abelianos o la categoría de espacios vectoriales sobre un campo dado) o en la categoría de grupos.

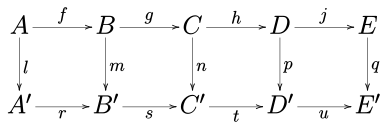
El lema de cinco establece que, si las filas son exactas, m y p son isomorfismos, l es un epimorfismo y q es un monomorfismo, entonces n también es un isomorfismo.

El lema de la serpiente

En una categoría abeliana (como la categoría de grupos abelianos o la categoría de espacios vectoriales sobre un campo dado), considere un diagrama conmutativo:

donde las filas son secuencias exactas y 0 es el objeto cero. Entonces hay una secuencia exacta que relaciona los núcleos y conúcleos de a, b y c: ${displaystyle ker ato ker bto ker c{overset {d}{to }}operatorname {coker} ato operatorname {coker} bto operatorname {coker} c}$

Además, si el morfismo f es un monomorfismo, entonces también lo es el morfismo ker a → ker b, y si g' es un epimorfismo, entonces también lo es coker b → coker c.

Categorías abelianas

En matemáticas, una categoría abeliana es una categoría en la que se pueden agregar morfismos y objetos y en la que existen núcleos y conúcleos y tienen propiedades deseables. El ejemplo prototipo motivador de una categoría abeliana es la categoría de grupos abelianos, Ab. La teoría se originó en un intento tentativo de unificar varias teorías de cohomología de Alexander Grothendieck. Las categorías abelianas son muy estables.categorías, por ejemplo son regulares y satisfacen el lema de la serpiente. La clase de categorías abelianas se cierra bajo varias construcciones categóricas, por ejemplo, la categoría de complejos de cadena de una categoría abeliana, o la categoría de funtores de una categoría pequeña a una categoría abeliana también son abelianos. Estas propiedades de estabilidad las hacen inevitables en álgebra homológica y más allá; la teoría tiene importantes aplicaciones en geometría algebraica, cohomología y teoría de categorías puras. Las categorías abelianas llevan el nombre de Niels Henrik Abel.

Más concretamente, una categoría es abeliana si

tiene un objeto cero,
tiene todos los productos binarios y coproductos binarios, y
tiene todos los kernels y cokernels.
todos los monomorfismos y epimorfismos son normales.

El funtor Ext

Sea R un anillo y sea Mod _R la categoría de módulos sobre R. Sea B en Mod _R y establezca T (B) = Hom _R (A,B), para A fijo en Mod _R. Este es un funtor exacto por la izquierda y por lo tanto tiene funtores derivados por la derecha R T. El funtor Ext está definido por $operatorname {Ext}_{R}^{n}(A,B)=(R^{n}T)(B).$

Esto se puede calcular tomando cualquier resolución inyectiva ${displaystyle 0rightarrow Brightarrow I^{0}rightarrow I^{1}rightarrow cdots,}$

y computación ${displaystyle 0rightarrow operatorname {Hom} _{R}(A,I^{0})rightarrow operatorname {Hom} _{R}(A,I^{1})rightarrow cdots.}$

Entonces (R T)(B) es la homología de este complejo. Tenga en cuenta que Hom _R (A,B) está excluido del complejo.

Se da una definición alternativa usando el funtor G (A)=Hom _R (A,B). Para un módulo fijo B, este es un funtor exacto por la izquierda contravariante y, por lo tanto, también tenemos funtores derivados por la derecha R G, y podemos definir $operatorname {Ext}_{R}^{n}(A,B)=(R^{n}G)(A).$

Esto se puede calcular eligiendo cualquier resolución proyectiva $puntos rightarrow P^{1}rightarrow P^{0}rightarrow Arightarrow 0,$

y procediendo dualmente calculando ${displaystyle 0rightarrow operatorname {Hom} _{R}(P^{0},B)rightarrow operatorname {Hom}_{R}(P^{1},B)rightarrow cdots.}$

Entonces (R G)(A) es la homología de este complejo. Nótese de nuevo que Hom _R (A,B) está excluido.

Estas dos construcciones dan resultados isomórficos, por lo que ambas pueden usarse para calcular el funtor Ext.

Funtor tor

Supongamos que R es un anillo y se denota por R - Mod la categoría de los módulos R izquierdos y por Mod - R la categoría de los módulos R derechos (si R es conmutativo, las dos categorías coinciden). Arreglar un módulo B en R - Mod. Para A en Mod - R, establezca T (A) = A ⊗ _R B. Entonces T es un funtor exacto derecho de Mod - Ra la categoría de grupos abelianos Ab (en el caso de que R sea conmutativo, es un funtor exacto por la derecha de Mod - R a Mod - R) y se definen sus funtores derivados por la izquierda L _n T. Nosotros fijamos $mathrm{Tor}_n^R(A,B)=(L_nT)(A)$

es decir, tomamos una resolución proyectiva $cdotsrightarrow P_2 rightarrow P_1 rightarrow P_0 rightarrow Arightarrow 0$

luego elimine el término A y tensor la resolución proyectiva con B para obtener el complejo $cdots rightarrow P_2otimes_R B rightarrow P_1otimes_R B rightarrow P_0otimes_R B rightarrow 0$

(note que A ⊗ _R B no aparece y la última flecha es solo el mapa cero) y tome la homología de este complejo.

Secuencia espectral

Fijar una categoría abeliana, como una categoría de módulos sobre un anillo. Una secuencia espectral es una elección de un número entero no negativo r ₀ y una colección de tres secuencias:

Para todos los números enteros r ≥ r ₀, un objeto E _r, llamado hoja (como en una hoja de papel), o a veces una página o un término,
Endomorfismos d _r: E _r → E _r que satisfacen d _r o d _r = 0, llamados mapas de límites o diferenciales,
Isomorfismos de E _r₊₁ con H (E _r), la homología de E _r con respecto a dr.

Una secuencia espectral doblemente graduada tiene una gran cantidad de datos para realizar un seguimiento, pero existe una técnica de visualización común que hace que la estructura de la secuencia espectral sea más clara. Tenemos tres índices, r, p y q. Para cada r, imagina que tenemos una hoja de papel cuadriculado. En esta hoja, tomaremos p como la dirección horizontal y q como la dirección vertical. En cada punto de la red tenemos el objeto $E_r^{p,q}$ .

Es muy común que n = p + q sea otro índice natural en la secuencia espectral. n corre en diagonal, de noroeste a sureste, a través de cada hoja. En el caso homológico, las diferenciales tienen bigrado (− r, r − 1), por lo que disminuyen n en uno. En el caso cohomológico, n se incrementa en uno. Cuando r es cero, el diferencial mueve los objetos un espacio hacia arriba o hacia abajo. Esto es similar al diferencial en un complejo de cadena. Cuando r es uno, el diferencial mueve los objetos un espacio hacia la izquierda o hacia la derecha. cuando res dos, el diferencial mueve objetos como el movimiento de un caballo en el ajedrez. Para r más alto, el diferencial actúa como un movimiento de caballo generalizado.

Funtor derivado

Supongamos que se nos da un funtor exacto izquierdo covariante F: A → B entre dos categorías abelianas A y B. Si 0 → A → B → C → 0 es una sucesión exacta corta en A, entonces aplicando F se obtiene la sucesión exacta 0 → F (A) → F (B) → F (C) y uno podría preguntarse cómo continuar esta secuencia hacia la derecha para formar una secuencia exacta larga. Estrictamente hablando, esta pregunta está mal planteada, ya que siempre hay numerosas formas diferentes de continuar una secuencia exacta dada hacia la derecha. Pero resulta que (si A es lo suficientemente "agradable") hay una forma canónica de hacerlo, dada por los funtores derivados por la derecha de F. Para todo i ≥1, existe un funtor R F: A → B, y la sucesión anterior continúa así: 0 → F (A) → F (B) → F (C) → R F (A) → R F (segundo) → R F (C) → R F (A) → R F (segundo) →.... De esto vemos que F es un funtor exacto si y sólo si R F = 0; entonces, en cierto sentido, los funtores derivados de la derecha de F miden "qué tan lejos" está F de ser exacto.

Funcionalidad

Un mapa continuo de espacios topológicos da lugar a un homomorfismo entre sus n -ésimos grupos de homología para todo n. Este hecho básico de la topología algebraica encuentra una explicación natural a través de ciertas propiedades de los complejos de cadenas. Dado que es muy común estudiar varios espacios topológicos simultáneamente, en el álgebra homológica se conduce a la consideración simultánea de múltiples cadenas complejas.

Un morfismo entre dos cadenas complejas, ${displaystyle F:C_{bullet }to D_{bullet },}$ es una familia de homomorfismos de grupos abelianos ${ estilo de visualización F_ {n}: C_ {n} a D_ {n}}$ que conmutan con los diferenciales, en el sentido de que ${displaystyle F_{n-1}circ d_{n}^{C}=d_{n}^{D}circ F_{n}}$ para todo n. Un morfismo de cadenas complejas induce un morfismo $H_bullet(F)$ de sus grupos de homología, que consiste en los homomorfismos ${displaystyle H_{n}(F):H_{n}(C)a H_{n}(D)}$ para todo n. Un morfismo F se denomina cuasi-isomorfismo si induce un isomorfismo en la n -ésima homología para todo n.

Muchas construcciones de cadenas complejas que surgen en álgebra y geometría, incluida la homología singular, tienen la siguiente propiedad de funcionalidad: si dos objetos X e Y están conectados por un mapa f, entonces las cadenas complejas asociadas están conectadas por un morfismo ${displaystyle F=C(f):C_{bullet }(X)to C_{bullet }(Y),}$ y, además, la composición $gcirc f$ de los mapas f: X → Y y g: Y → Z inducen el morfismo ${displaystyle C(gcirc f):C_{bullet }(X)to C_{bullet }(Z)}$ que coincide con la composición ${displaystyle C(g)circ C(f).}$ Se sigue que los grupos de homología $H_bullet(C)$ son también functoriales, por lo que los morfismos entre objetos algebraicos o topológicos dan lugar a mapas compatibles entre su homología.

La siguiente definición surge de una situación típica en álgebra y topología. Un triple que consta de tres cadenas complejas $L_bullet, M_bullet, N_bullet$ y dos morfismos entre ellos, $f:L_bulleta M_bullet, g: M_bulleta N_bullet,$ se llama un triple exacto, o una secuencia exacta corta de complejos, y se escribe como ${displaystyle 0longrightarrow L_{bullet}}{overset {f}{longrightarrow}}M_{bullet}{overset {g}{longrightarrow}}N_{bullet}longrightarrow 0,}$

si para cualquier n, la secuencia ${displaystyle 0longrightarrow L_{n}{overset {f_{n}}{longrightarrow }}M_{n}{overset {g_{n}}{longrightarrow }}N_{n}longrightarrow 0}$

es una sucesión exacta corta de grupos abelianos. Por definición, esto significa que f _n es una inyección, g _n es una sobreyección e Im f _n = Ker g _n. Uno de los teoremas más básicos del álgebra homológica, a veces conocido como lema en zig-zag, establece que, en este caso, hay una secuencia exacta larga en la homología. ${displaystyle cdots longrightarrow H_{n}(L){overset {H_{n}(f)}{longrightarrow }}H_{n}(M){overset {H_{n}(g)} { longrightarrow }}H_{n}(N){overset {delta _{n}}{longrightarrow }}H_{n-1}(L){overset {H_{n-1}(f) }{longrightarrow }}H_{n-1}(M)longrightarrow cdots,}$

donde los grupos de homología de L, M y N se suceden cíclicamente, y δ _n son ciertos homomorfismos determinados por f y g, llamados homomorfismos de conexión. Las manifestaciones topológicas de este teorema incluyen la secuencia de Mayer-Vietoris y la secuencia exacta larga para la homología relativa.

Aspectos fundacionales

Las teorías de cohomología se han definido para muchos objetos diferentes, como espacios topológicos, haces, grupos, anillos, álgebras de Lie y álgebras C*. El estudio de la geometría algebraica moderna sería casi impensable sin la cohomología de haces.

Central al álgebra homológica es la noción de secuencia exacta; estos se pueden utilizar para realizar cálculos reales. Una herramienta clásica del álgebra homológica es la del funtor derivado; los ejemplos más básicos son los funtores Ext y Tor.

Con un conjunto diverso de aplicaciones en mente, era natural tratar de poner todo el tema sobre una base uniforme. Hubo varios intentos antes de que el tema se calmara. Una historia aproximada se puede establecer de la siguiente manera:

Cartan-Eilenberg: En su libro de 1956 "Álgebra homológica", estos autores utilizaron resoluciones de módulos proyectivos e inyectivos.
'Tohoku': El enfoque en un célebre artículo de Alexander Grothendieck que apareció en la Segunda Serie del Tohoku Mathematical Journal en 1957, utilizando el concepto de categoría abeliana (para incluir haces de grupos abelianos).
La categoría derivada de Grothendieck y Verdier. Las categorías derivadas se remontan a la tesis de Verdier de 1967. Son ejemplos de categorías trianguladas utilizadas en varias teorías modernas.

Estos pasan de la computabilidad a la generalidad.

El mazo computacional por excelencia es la secuencia espectral; estos son esenciales en los enfoques de Cartan-Eilenberg y Tohoku donde se necesitan, por ejemplo, para calcular los funtores derivados de una composición de dos funtores. Las secuencias espectrales son menos esenciales en el enfoque de categorías derivadas, pero aún desempeñan un papel cuando se necesitan cálculos concretos.

Ha habido intentos de teorías 'no conmutativas' que extienden la primera cohomología como torsors (importante en la cohomología de Galois).

Contenido relacionado

Más resultados...