Abscisa y ordenada
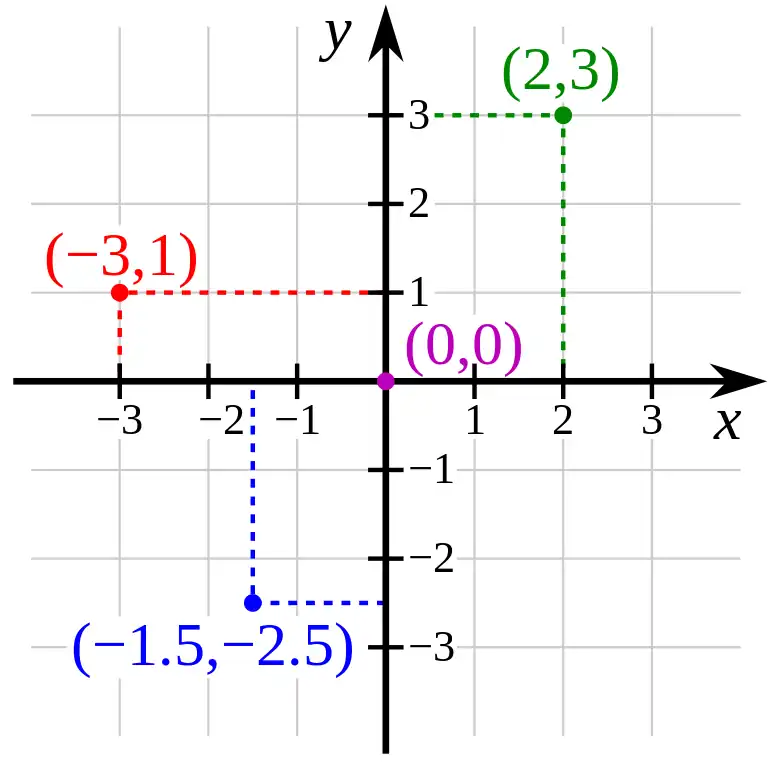
Abscisa y ordenada, son las dos coordenadas de los ejes principales de un sistema de coordenadas bidimensional (2D), que permiten ubicar un punto dentro del sistema. La abscisa es la coordenada horizontal y se representa habitualmente por la letra X, indicando la posición en el eje horizontal, mientras que la ordenada es la coordenada vertical y se representa por la Y, indicando la posición en el eje vertical.
Formalmente, la distancia de un punto desde el Eje y, medida y escalada con el Eje x, se llama abscisa o coordenada x del punto. La distancia de un punto desde el Eje x, medida y escalada con el Eje y se denomina ordenada. También puede decirse que la abscisa es simplemente otra manera de referirse a la coordenada X de un punto (derecha o izquierda) y la ordenada otra manera de referirse a la coordenada Y (arriba o abajo).
Por ejemplo, para un punto dado como un par ordenado (x, y) en el plano cartesiano, entonces la primera coordenada en el plano (o sea x) se llama abscisa y la segunda coordenada (o sea y) es la ordenada.
En matemáticas, la abscisa y la ordenada son siempre respectivamente la primera y la segunda coordenada de un punto en un sistema de coordenadas cartesianas:
Abscisa = Eje X (horizontal)
Ordenada = Eje Y (vertical)
Definición formal
Para un sistema coordenado bidimensional:
La abscisa de un punto es la medida con signo de su proyección sobre el eje principal, cuyo valor absoluto es la distancia entre la proyección y el origen del eje, y cuyo signo viene dado por la ubicación de la proyección con respecto al origen (antes: negativo; después: positivo).
La ordenada de un punto es la medida con signo de su proyección sobre el eje secundario, cuyo valor absoluto es la distancia entre la proyección y el origen del eje, y cuyo signo viene dado por la ubicación de la proyección con respecto al origen (antes: negativo; después: positivo).
Ejemplos
Ejemplo 1
Para denotar lo que se denomina un par ordenado, se usa la notación (x, y), por ejemplo (2, 4), donde 2 representa la abscisa (x) y 4 la ordenada (y). Si pensamos en las posiciones que ocupan los pares ordenados (4, 2) y (2, 4) en el plano cartesiano (ver figura siguiente), entonces es inmediatamente evidente por qué el orden de la abscisa y ordenada es importante. El par ordenado (4, 2) simplemente no es lo mismo que el par ordenado (2, 4).
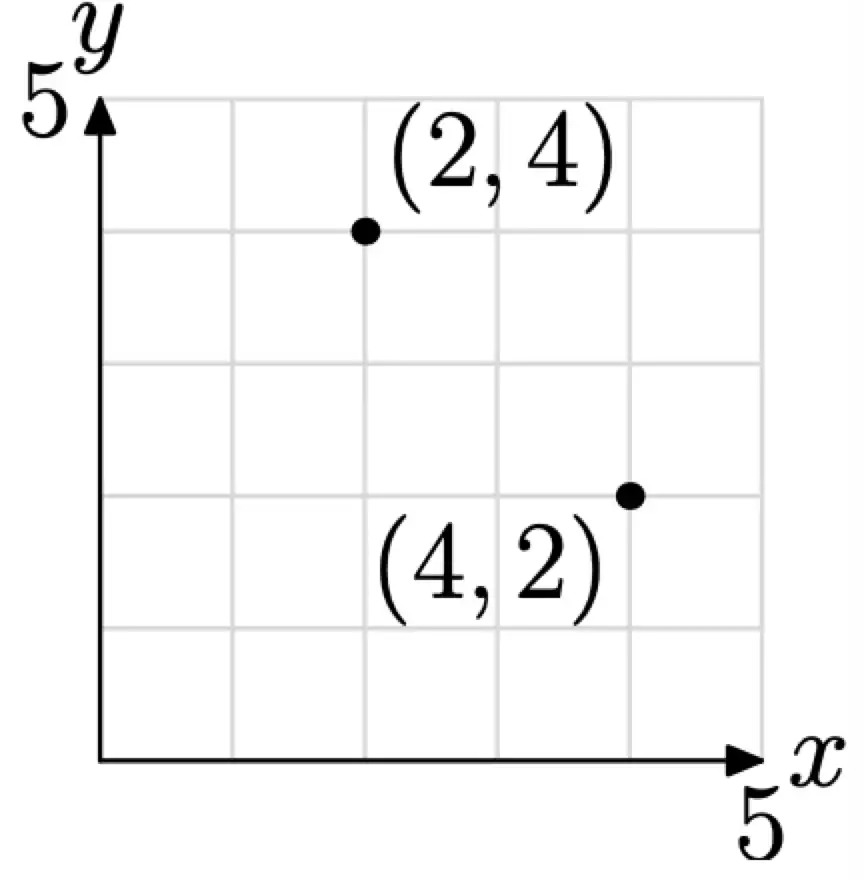
El primer elemento de un par ordenado se llama siempre su abscisa. El segundo elemento de un par ordenado se llama siempre su ordenada. Así, por ejemplo, para hallar la abscisa de (4, 2) simplemente separamos el primer elemento: 4, mientras que la ordenada de (4, 2) es el segundo: 2.
Ejemplo 2
Considérese la gráfica de la relación S que se muestra en la siguiente figura, hay cinco pares ordenados (puntos) trazados en la figura, ellos son (1, 2), (2, 1), (2, 4), (3, 3) y (4, 4).
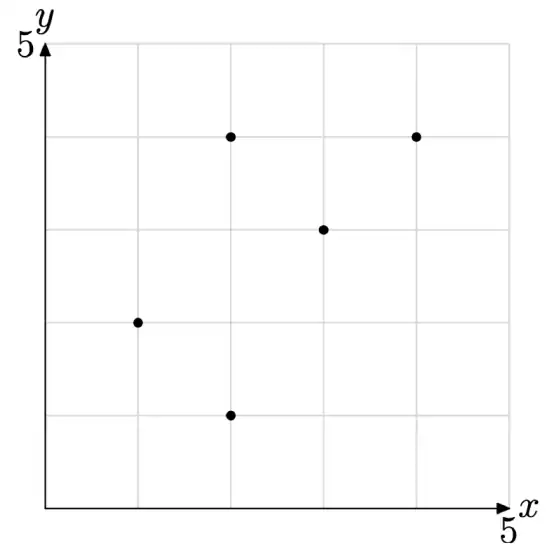
y = {1, 2, 3, 4}
Por lo tanto, la relación S con Dominio = {1, 2, 3, 4} y Rango = {1, 2, 3, 4} tiene el valor S = {(1, 2), (2, 1), (2, 4), (3, 3), (4, 4)}. En el caso del rango, observe cómo se han ordenado las ordenadas de cada par ordenado en orden ascendente, teniendo cuidado de no enumerar ninguna ordenada más de una vez.
Aplicaciones
En matemáticas, las abscisas y ordenadas son la base de la geometría analítica, permitiendo representar figuras geométricas mediante ecuaciones y fórmulas. Esto facilita el estudio de sus propiedades, como áreas, perímetros y distancias, además de posibilitar la resolución de problemas geométricos de manera algebraica. El sistema de coordenadas cartesianas también es esencial en el cálculo, donde se utiliza para graficar funciones y analizar su comportamiento, como máximos, mínimos y puntos de inflexión.
En física, las abscisas y ordenadas son fundamentales para describir el movimiento de los objetos y la relación entre diferentes magnitudes. Por ejemplo, en un gráfico de velocidad vs. tiempo, la abscisa representa el tiempo y la ordenada la velocidad, permitiendo visualizar cómo cambia la velocidad a lo largo del tiempo. Asimismo, en el estudio de la cinemática y la dinámica, las coordenadas cartesianas son esenciales para representar las posiciones, velocidades y aceleraciones de los cuerpos en movimiento.
En ingeniería, las abscisas y ordenadas son herramientas indispensables en el diseño y modelado de estructuras y sistemas. Por ejemplo, en ingeniería civil, se utilizan para representar la ubicación de puntos en un terreno y diseñar planos de construcción. En ingeniería mecánica, se emplean para analizar las fuerzas y tensiones en estructuras, como puentes y edificios. Además, en el diseño de software y sistemas de navegación, las coordenadas cartesianas son fundamentales para representar la ubicación de objetos en un espacio virtual o real.
En Ecuaciones paramétricas
En una variante de uso algo obsoleta, la abscisa de un punto también puede referirse a cualquier número que describa la ubicación del punto a lo largo de alguna ruta, p. el parámetro de una ecuación paramétrica. Usada de esta manera, la abscisa se puede considerar como una geometría de coordenadas análoga a la variable independiente en un modelo o experimento matemático (cualquier ordenada cumple un papel análogo a las variables dependientes).
Historia
Aunque la palabra abscissa (latín: "línea cortada") se ha utilizado al menos desde De Practica Geometrie publicado en 1220 por Fibonacci (Leonardo de Pisa), su uso en su sentido moderno puede deberse al matemático veneciano Stefano degli Angeli en su obra Miscellaneum Hyperbolicum, et Parabolicum de 1659.
En su obra de 1892 Vorlesungen über die Geschichte der Mathematik (Conferencias sobre historia de las matemáticas"), volumen 2, el historiador alemán de las matemáticas Moritz Cantor escribe:
Sin embargo, [Stefano degli Angeli] probablemente introdujo una palabra en el vocabulario matemático que ha demostrado ser prometedora, especialmente en geometría analítica. […] No conocemos un uso anterior de la palabra "abscisa" en escritos latinos originales. Quizás la palabra aparece en traducciones de las "Cónicas" de Apolonio, donde en el Libro I, Proposición 20, se menciona "ἀποτεμνομέναις", para lo cual difícilmente habría una palabra latina más adecuada que "abscisa".
El uso de la palabra "ordenadas" está relacionado con la frase latina "linea ordinata applicata", o "línea aplicada paralela".
Contenido relacionado
Conjunto vacío
Historia de la lógica
Función monótona
