Zona fresnel

Varios ejemplos de cómo las zonas de Fresnel pueden ser interrumpidas

Una zona de Fresnel (fray-NEL), llamada así por el físico Augustin-Jean Fresnel, es una de una serie de regiones elipsoidales alargadas confocales del espacio entre y alrededor de un transmisor y un receptor. La onda primaria viajará en una línea relativamente recta desde el transmisor hasta el receptor. Las ondas de radio, sonido o luz transmitidas de manera aberrante que se transmiten al mismo tiempo pueden seguir caminos ligeramente diferentes antes de llegar a un receptor, especialmente si hay obstrucciones u objetos que se desvían entre los dos. Las dos ondas pueden llegar al receptor en momentos ligeramente diferentes y la onda aberrante puede llegar fuera de fase con la onda primaria debido a las diferentes longitudes de trayectoria. Dependiendo de la magnitud de la diferencia de fase entre las dos ondas, las ondas pueden interferir de manera constructiva o destructiva. El tamaño de la zona de Fresnel calculada a cualquier distancia particular del transmisor y el receptor puede ayudar a predecir si las obstrucciones o discontinuidades a lo largo de la ruta causarán una interferencia significativa.

Importancia

En cualquier transmisión propulsada por onda entre un transmisor y receptor, cierta cantidad de la onda radiada se propaga fuera del eje (no en la línea de visión entre transmisor y receptor). Esto puede entonces desviar objetos y luego irradiar al receptor. Sin embargo, la onda de vía directa y la onda desviada pueden llegar fuera de fase, lo que conduce a una interferencia destructiva cuando la diferencia de fase es medio entero extraño (()2z+1)/2,z▪ ▪ Z{displaystyle {(2z+1)/2,zin mathbb {Z}}) múltiples del período. La zona n-th Fresnel se define como el lacus de puntos en el espacio 3D, de tal manera que un camino de 2 segmentos del transmisor al receptor que desvía un punto en esa superficie será entre n-1 y n media onda longitudes fuera de fase con el camino de línea recta. Los límites de estas zonas serán elipsoides con foci en el transmisor y receptor. Para garantizar una interferencia limitada, estas vías de transmisión están diseñadas con cierta distancia de limpieza determinada por un análisis de la zona de Fresnel.

La dependencia de la interferencia en el espacio libre es la causa del efecto de cercado cuando el transmisor de radio o el receptor están en movimiento, y las zonas de intensidad de señal alta y baja están por encima y por debajo del corte del receptor. límite. Las variaciones extremas de la intensidad de la señal en el receptor pueden causar interrupciones en el enlace de comunicaciones o incluso impedir que se reciba una señal.

Las zonas de Fresnel se ven en óptica, radiocomunicaciones, electrodinámica, sismología, acústica, radiación gravitacional y otras situaciones que involucran la radiación de ondas y la propagación de trayectos múltiples. Los cálculos de zona de Fresnel se utilizan para anticipar las distancias libres de obstáculos requeridas al diseñar sistemas altamente directivos, como los sistemas de antenas parabólicas de microondas. Aunque intuitivamente, una línea de visión clara entre el transmisor y el receptor puede parecer todo lo que se requiere para un sistema de antena fuerte, pero debido a la naturaleza compleja de las ondas de radio, las obstrucciones dentro de la primera zona de Fresnel pueden causar una debilidad significativa, incluso si esas obstrucciones no bloquean la ruta de la señal de línea de visión aparente. Por esta razón, es valioso hacer un cálculo del tamaño de la primera zona de Fresnel, o primaria, para un sistema de antena dado. Hacer esto permitirá que el instalador de la antena decida si un obstáculo, como un árbol, tendrá un impacto significativo en la intensidad de la señal. La regla general es que la zona principal de Fresnel estaría idealmente libre de obstáculos en un 80 %, pero debe estar libre de obstáculos al menos en un 60 %.

Estructura espacial

First Fresnel zone avoidance

Las zonas de Fresnel son regiones de forma elipsoidal alargada confocal en el espacio (por ejemplo, 1, 2, 3), centradas alrededor de la línea de la ruta de transmisión directa (ruta AB en el diagrama). La primera región incluye el espacio elipsoidal por el que pasa la señal de línea de visión directa. Si un componente perdido de la señal transmitida rebota en un objeto dentro de esta región y luego llega a la antena receptora, el cambio de fase será algo menor que un cuarto de longitud de onda, o menos de un cambio de 90º (ruta ACB en el diagrama). El efecto con respecto al cambio de fase solo será mínimo. Por lo tanto, esta señal rebotada puede potencialmente tener un impacto positivo en el receptor, ya que está recibiendo una señal más fuerte de lo que hubiera sido sin la deflexión, y la señal adicional potencialmente estará en su mayor parte en fase. Sin embargo, los atributos positivos de esta desviación también dependen de la polarización de la señal en relación con el objeto (consulte la sección sobre polarización en la pestaña Hablar).

La segunda región rodea a la primera pero la excluye. Si un objeto reflectante se encuentra en la segunda región, la onda sinusoidal perdida que ha rebotado en este objeto y ha sido capturada por el receptor se desplazará más de 90º pero menos de 270º debido al aumento de la longitud de la trayectoria y, potencialmente, será recibido fuera de fase. Generalmente esto es desfavorable. Pero, de nuevo, esto depende de la polarización (consulte la sección sobre polarización en la pestaña Hablar). El uso de la misma polarización circular (p. ej., la derecha) en ambos extremos eliminará un número impar de reflejos (incluido uno).

La tercera región rodea a la segunda región y las ondas desviadas capturadas por el receptor tendrán el mismo efecto que una onda en la primera región. Es decir, la onda sinusoidal se habrá desplazado más de 270º pero menos de 450º (lo ideal sería un desplazamiento de 360º) y por tanto llegará al receptor con el mismo desplazamiento que podría llegar una señal desde la 1ª región. Una onda desviada de esta región tiene el potencial de desplazarse con precisión una longitud de onda para que esté exactamente sincronizada con la onda de la línea de visión cuando llegue a la antena receptora.

La cuarta región rodea a la tercera región y es similar a la segunda región. Y así.

Si no hay obstrucciones y se encuentra en un entorno perfecto, las ondas de radio viajarán en una línea relativamente recta desde el transmisor hasta el receptor. Pero si hay superficies reflectantes que interactúan con una onda perdida transmitida, como masas de agua, terrenos lisos, techos, costados de edificios, etc., las ondas de radio que se desvían de esas superficies pueden llegar desfasadas o desfasadas. -fase con las señales que viajan directamente al receptor. A veces, esto da como resultado el hallazgo contrario a la intuición de que reducir la altura de una antena aumenta la relación señal-ruido en el receptor.

Aunque las ondas de radio generalmente viajan relativamente en línea recta, la niebla e incluso la humedad pueden hacer que parte de la señal en ciertas frecuencias se disperse o se doble antes de llegar al receptor. Esto significa que los objetos que están fuera de la línea de visión seguirán bloqueando potencialmente partes de la señal. Para maximizar la intensidad de la señal, es necesario minimizar el efecto de la pérdida de obstrucción eliminando los obstáculos tanto de la línea de visión directa de radiofrecuencia (RF LoS) como del área a su alrededor dentro de la zona principal de Fresnel. Las señales más fuertes están en la línea directa entre el transmisor y el receptor y siempre se encuentran en la primera zona de Fresnel.

A principios del siglo XIX, el científico francés Augustin-Jean Fresnel creó un método para calcular dónde están las zonas, es decir, si un obstáculo determinado causará desviaciones principalmente en fase o fuera de fase entre el transmisor y El receptor.

Cálculo de espacio libre

Zona de fresnel: D es la distancia entre el transmisor y el receptor; r es el radio de la primera zona de Fresnel (n=1) en el punto P. P está d1 lejos del transmisor, y d2 lejos del receptor.

El concepto de zona libre de Fresnel se puede utilizar para analizar la interferencia de obstáculos cerca de la trayectoria de un haz de radio. La primera zona debe mantenerse en gran parte libre de obstrucciones para evitar interferir con la recepción de radio. Sin embargo, a menudo se puede tolerar cierta obstrucción de las zonas de Fresnel. Como regla general, la obstrucción máxima permitida es del 40 %, pero la obstrucción recomendada es del 20 % o menos.

Para establecer zonas de Fresnel, primero determine la línea de vista de RF (RF LoS), que en términos simples es una línea recta entre las antenas transmisora y receptora. Ahora se dice que la zona que rodea el RF LoS es la zona de Fresnel. El radio de la sección transversal de cada zona de Fresnel es más largo en el punto medio de RF LoS, y se reduce a un punto en cada vértice, detrás de las antenas.

Formulación

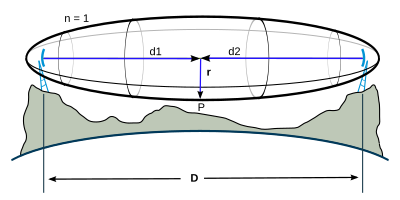
Considerar un punto arbitrario P en el LoS, a una distancia d1{displaystyle D_{1} y d2{displaystyle D_{2} con respecto a cada una de las dos antenas. Para obtener el radio rn{displaystyle R_{n} zona n{displaystyle n}, note que el volumen de la zona está delimitado por todos los puntos para los cuales la diferencia en distancias, entre la onda directa (D=d1+d2{displaystyle D=d_{1}+d_{2}) y la onda reflejada (AP̄ ̄ +PB̄ ̄ {displaystyle {fnMicrosoft Sans Serif} {fnK}} {fnMicrosoft Sans Serif}) es la constante nλ λ 2{displaystyle n{frac {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft\\\fnMicrosoft\\\\\fnMicrosoft\\\\\fnMicrosoft\\\\\\\\\\\\\\\\\fnMinMicrosoft\\\\\\\\\\\\\\\\\\\\\\\\\\\fnMicrosoft\\\\\\\\\\\\\\\\\\\\\fnMin } {2}} (multiples de media longitud de onda). Esto define efectivamente un elipsoide con el eje principal a lo largo AB̄ ̄ {displaystyle {fnMicrosoft}} y foci en las antenas (puntos A y B). Entonces:

AP̄ ̄ +PB̄ ̄ − − D=nλ λ 2{displaystyle {fnK}+{fn}-D=n{frac} {fnMicrode } {2}}

Reescribir la expresión con las coordenadas de punto P{displaystyle P} y la distancia entre las antenas D{displaystyle D}, da:

d12+rn2+d22+rn2− − ()d1+d2)=nλ λ 2{displaystyle {sqrt {fn} {fn} {fn} {fn}} {fn}}} {\fn}}}}} { sqrt}}}}} {\fn}}}}}}} {\fn}}} {\\fn}}}}}}}}}\\\n}}}}}}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ [d_{2} {2}+r_{n} {2}}-(d_{1}+d_{2}=n{frac} {fnMicrode } {2}}

d1()1+rn2/d12− − 1)+d2()1+rn2/d22− − 1)=nλ λ 2{displaystyle d_{1}left({sqrt {1+r_{2}/d_{1} {2}}-1right)+d_{2}left({sqrt) {1+r_{2}/d_{2} {2}}-1right)=n{frac} {fnMicrode } {2}}

Asumiendo las distancias entre las antenas y el punto P{displaystyle P} son mucho más grandes que el radio y aplicando la aproximación binomial para la raíz cuadrada, 1+x.. 1+x/2{displaystyle {sqrt {1+x}approx 1+x/2} (por x≪1), la expresión simplifica:

rn22()1d1+1d2).. nλ λ 2{displaystyle {frac {fn}{2}}left({frac} {fn} {fn} {fn} {fn}} {fn}}} {fn}}}}fn}}}f}fn}f}fn}fnKfn}fn}}f}fn}fn}fn}fn}fn}fnh}fn}fn}fn}fn}fn}fnh}fn}fn}fn}fn}fnh}fn}fn}fn}fnhn}fnh}fn}fn}fn}fn}fnh}fn}fn}fnh}fnh}fn}fn}fn}fnh}fn}fn {1}{d_{1}}+{frac} Vale. No. } {2}}

que se puede resolver para rn{displaystyle R_{n}:

rn.. nd1d2Dλ λ ,d1,d2≫ ≫ nλ λ ,{displaystyle r_{n}approx {fnMicroc} {d_{1} {2} {}lambda}quad d_{1},d_{2}gg nlambda}

Para un enlace de satélite a tierra, se simplifica aún más a:

rn.. nd1λ λ ,d1≫ ≫ nλ λ ,d2.. D{displaystyle r_{n}approx {fn}fn}fnK} D_{2}approx D}

Espacio máximo

Para aplicaciones prácticas, a menudo es útil conocer el radio máximo de la primera zona de Fresnel. Uso n=1{displaystyle n=1}, d1=d2=D/2{displaystyle D_{1}=d_{2}=D/2, y λ λ =c/f{displaystyle lambda =c/f} en la fórmula anterior

F1=12λ λ D=12cDf,{displaystyle F_{1}={1over 2}{sqrt {lambda D}={1 over 2}{sqrt {cD over f}}} {f}}

dónde

D{displaystyle D} es la distancia entre las dos antenas,

f{displaystyle f} es la frecuencia de la señal transmitida,

c{displaystyle c}. 2.997×10⁸m/s es la velocidad de la luz en el aire.

Sustitución del valor numérico para c{displaystyle c} seguido de una conversión de unidad resulta en una manera fácil de calcular el radio de la primera zona de Fresnel F1{displaystyle F_{1}, conocer la distancia entre las dos antenas D{displaystyle D} y la frecuencia de la señal transmitida f{displaystyle f}:

• F1[m]=8.656D[km]f[GHz]{displaystyle F_{1}mathrm {[m]} =8.656{sqrt {Dmathrm {[km]over fmathrm {[GHz]}}}}
• F1[ft]=36.03D[mi]f[GHz]{displaystyle F_{1}mathrm {} =36.03{sqrt {Dmathrm {[mi]} {}}