Unión cooperativa

Compartir Imprimir Citar

Mecanismo molecular

unión cooperativa se produce en sistemas de unión molecular que contienen más de un tipo o especie de molécula y en los que uno de los socios no es monovalente y puede unirse a más de una molécula del otro. especies. En general, la unión molecular es una interacción entre moléculas que da como resultado una asociación física estable entre esas moléculas.

La unión cooperativa se produce en un sistema de unión molecular en el que dos o más moléculas de ligando pueden unirse a una molécula de receptor. La vinculación puede considerarse "cooperativa" si la unión real de la primera molécula del ligando al receptor cambia la afinidad de unión de la segunda molécula del ligando. La unión de moléculas de ligando a los diferentes sitios de la molécula receptora no constituyen eventos mutuamente independientes. La cooperatividad puede ser positiva o negativa, lo que significa que es más o menos probable que las sucesivas moléculas de ligando se unan a la molécula receptora.

La unión cooperativa se observa en muchos biopolímeros, incluidas las proteínas y los ácidos nucleicos. Se ha demostrado que la unión cooperativa es el mecanismo subyacente a una amplia gama de procesos bioquímicos y fisiológicos.

Historia y formalismos matemáticos

Christian Bohr y el concepto de unión cooperativa

En 1904, Christian Bohr estudió la unión de la hemoglobina al oxígeno en diferentes condiciones. Al trazar la saturación de hemoglobina con oxígeno en función de la presión parcial de oxígeno, obtuvo una curva sigmoidea (o en forma de 'S'). Esto indica que cuanto más oxígeno se une a la hemoglobina, más fácil es que se una más oxígeno, hasta que todos los sitios de unión estén saturados. Además, Bohr notó que el aumento de la presión de CO2 desplazaba esta curva hacia la derecha, es decir, las concentraciones más altas de CO₂ dificultan que la hemoglobina se una al oxígeno. Este último fenómeno, junto con la observación de que la afinidad de la hemoglobina por el oxígeno aumenta al aumentar el pH, se conoce como efecto Bohr.

Figura original de Christian Bohr, mostrando el aumento sigmoidal de la oxihemoglobina como función de la presión parcial del oxígeno.

Se dice que una molécula receptora exhibe unión cooperativa si su unión a escalas de ligando no linealmente con concentración de ligando. La cooperación puede ser positiva (si la unión de una molécula de ligando aumenta la afinidad aparente del receptor, y por lo tanto aumenta la probabilidad de otra unión de molécula de ligando) o negativa (si la unión de una molécula de ligando disminuye la afinidad y por lo tanto hace menos probable la unión de otras moléculas de ligando). La ocupación fraccional ${bar {Y}}$ de un receptor con un ligando dado se define como la cantidad de sitios de unión de ligando divididos por la cantidad total de sitios de unión de ligando:

{bar {Y}}={frac {[{text{bound sites}}]}{[{text{bound sites}}]+[{text{unbound sites}}]}}={frac {[{text{bound sites}}]}{[{text{total sites}}]}}

Si ${bar {Y}}=0$ , entonces la proteína está completamente desbordada, y si ${bar {Y}}=1$ Está completamente saturada. Si la trama de ${bar {Y}}$ en el equilibrio como función de la concentración de ligando es en forma sigmoidal, como observa Bohr para la hemoglobina, esto indica la cooperación positiva. Si no lo es, no se puede hacer ninguna declaración sobre la cooperación de mirar esta parcela solo.

El concepto de unión cooperativa solo se aplica a moléculas o complejos con más de un sitio de unión a ligando. Si existen varios sitios de unión del ligando, pero la unión del ligando a cualquier sitio no afecta a los demás, se dice que el receptor no coopera. La cooperatividad puede ser homotrópica, si un ligando influye en la unión de ligandos del mismo tipo, o heterotrópica, si influye en la unión de otros tipos de ligandos. En el caso de la hemoglobina, Bohr observó una cooperatividad positiva homotrópica (la unión de oxígeno facilita la unión de más oxígeno) y una cooperatividad negativa heterotrópica (la unión de CO₂ reduce la capacidad de la hemoglobina para unir oxígeno).

A lo largo del siglo XX, se han desarrollado varios marcos para describir la unión de un ligando a una proteína con más de un sitio de unión y los efectos cooperativos observados en este contexto.

La ecuación de Hill

La primera descripción de la unión cooperativa a una proteína multisitio fue desarrollada por A.V. Colina. Basándose en las observaciones de la unión del oxígeno a la hemoglobina y la idea de que la cooperatividad surgió de la agregación de moléculas de hemoglobina, cada una de las cuales se une a una molécula de oxígeno, Hill sugirió una ecuación fenomenológica que desde entonces lleva su nombre:

Hill plot of the Hill ecuación en rojo, mostrando la pendiente de la curva siendo el coeficiente Hill y la interceptación con el eje x que proporciona la aparente constante de disociación. La línea verde muestra la curva no cooperativa.

{bar {Y}}={frac {Kcdot {}[X]^{n}}{1+Kcdot {}[X]^{n}}}={frac {[X]^{n}}{K^{*}+[X]^{n}}}={frac {[X]^{n}}{K_{d}^{n}+[X]^{n}}}

Donde $n$ es el "Coeficiente de Hill", $[X]$ denota concentración de ligando, $K$ denota una constante asociación aparente (utilizada en la forma original de la ecuación), $K^{*}$ es una constante de disociación empírica, y $K_{d}$ una constante de disociación microscópica (utilizada en formas modernas de la ecuación, y equivalente a una ${mathrm {EC}}_{{50}}$ ). Si $<math alttext="{displaystyle nn.1{displaystyle n made1} <img alt="n$ , el sistema exhibe la cooperación negativa, mientras que la cooperación es positiva si $1}" xmlns="http://www.w3.org/1998/Math/MathML">n■1{displaystyle n confía1}1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ee74e1cc07e7041edf0fcbd4481f5cd32ad17b64" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/>$ . El número total de sitios ligando es un límite superior para $n$ . La ecuación Hill puede ser linealizada como:

log {frac {{bar {Y}}}{1-{bar {Y}}}}=ncdot {}log[X]-ncdot {}log K_{d}

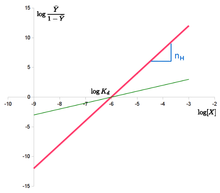
El "Hill plot" se obtiene trazando $log {frac {{bar {Y}}}{1-{bar {Y}}}}$ versus $log[X]$ . En el caso de la ecuación Hill, es una línea con pendiente $n_{H}$ e interceptación $log(K_{d})$ . Esto significa que la cooperación se supone que se fija, es decir, que no cambia con la saturación. También significa que los sitios de unión siempre exhiben la misma afinidad, y la cooperatividad no surge de una afinidad aumentando con la concentración de ligando.

La ecuación de Adair

G.S. Adair encontró que la trama de Hill para la hemoglobina no era una línea recta, e hipótesis de que la afinidad vinculante no era un término fijo, sino dependiente de la saturación de ligando. Habiendo demostrado que la hemoglobina contenía cuatro hemos (y por lo tanto sitios vinculantes para el oxígeno), trabajó desde la suposición de que la hemoglobina totalmente saturada se forma en etapas, con formas intermedias con una, dos o tres moléculas de oxígeno ligadas. La formación de cada etapa intermedia de la hemoglobina sin límites se puede describir utilizando una aparente constante de asociación macroscópica $K_{i}$ . La ocupación fraccional resultante puede expresarse como:

{bar {Y}}={frac {1}{4}}cdot {}{frac {K_{I}[X]+2K_{{II}}[X]^{2}+3K_{{III}}[X]^{3}+4K_{{IV}}[X]^{4}}{1+K_{I}[X]+K_{{II}}[X]^{2}+K_{{III}}[X]^{3}+K_{{IV}}[X]^{4}}}

O, para cualquier proteína con sitios de unión al ligando n:

{bar {Y}}={frac {1}{n}}{frac {K_{I}[X]+2K_{{II}}[X]^{2}+ldots +nK_{{n}}[X]^{n}}{1+K_{I}[X]+K_{{II}}[X]^{2}+ldots +K_{n}[X]^{n}}}

Donde n denota el número de sitios vinculantes y cada uno $K_{i}$ es una constante de asociación combinada, describiendo la unión de i moléculas de ligando. Al combinar el tratamiento de Adair con la trama Hill, se llega a la definición experimental moderna de la cooperación (Hill, 1985, Abeliovich, 2005). El resultado Coeficiente de colina, o más correctamente la pendiente de la parcela de Hill calculada a partir de la Ecuación de Adair, se puede demostrar que es la relación entre la variabilidad del número de unión a la varianza del número de unión en un sistema equivalente de sitios de unión no interaccionante. Así, el coeficiente Hill define la cooperatividad como una dependencia estadística de un sitio vinculante en el estado de otros sitios.

La ecuación de Klotz

Trabajando en proteínas de unión de calcio, Irving Klotz deconvolutó las constantes de asociación de Adair considerando la formación gradual de las etapas intermedias, e intentó expresar la unión cooperativa en términos de procesos elementales gobernados por la ley de acción masiva. En su marco, $K_{1}$ es la unión constante de unión de la primera molécula ligando, $K_{2}$ la unión constante de unión de la segunda molécula de ligando (una vez que la primera ya está ligada) etc. Para ${bar {Y}}$ , esto da:

{displaystyle {bar {Y}}={frac {1}{n}}{frac {K_{1}[X]+2K_{1}K_{2}[X]^{2}+ldots +nleft(K_{1}K_{2}ldots K_{n}right)[X]^{n}}{1+K_{1}[X]+K_{1}K_{2}[X]^{2}+ldots +left(K_{1}K_{2}ldots K_{n}right)[X]^{n}}}}

Vale la pena señalar que las constantes $K_{1}$ , $K_{2}$ y así sucesivamente no se relacionan con sitios de unión individuales. Ellos describen cuántos sitios vinculantes están ocupados, en lugar de cuáles. Esta forma tiene la ventaja de que la cooperación es fácilmente reconocida al considerar las constantes de la asociación. Si todos los sitios de unión ligand son idénticos con una constante de asociación microscópica $K$ , uno esperaría $K_{1}=nK,K_{2}={frac {n-1}{2}}K,ldots K_{n}={frac {1}{n}}K$ (Eso es $K_{i}={frac {n-i+1}{i}}K$ ) en ausencia de cooperación. Tenemos una cooperación positiva si $K_{i}$ sobre estos valores previstos $1}" xmlns="http://www.w3.org/1998/Math/MathML">i■1{displaystyle i confía1}1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/dea233301b9ca8fe5dde94824f918c0ceaf7fd5f" style="vertical-align: -0.338ex; width:5.063ex; height:2.176ex;"/>$ .

La ecuación de Klotz (que a veces también se denomina ecuación de Adair-Klotz) todavía se usa a menudo en la literatura experimental para describir las mediciones de la unión de ligandos en términos de constantes de unión aparentes secuenciales.

Ecuación de Pauling

A mediados del siglo XX, había un mayor interés en los modelos que no sólo describirían curvas vinculantes fenomenológicamente, sino que ofrecían un mecanismo bioquímico subyacente. Linus Pauling reinterpretó la ecuación proporcionada por Adair, asumiendo que sus constantes eran la combinación de la constante de unión para el ligand ( $K$ en la ecuación de abajo) y energía proveniente de la interacción entre subunidades de la proteína cooperativa ( $alpha$ infra). Pauling realmente obtuvo varias ecuaciones, dependiendo del grado de interacción entre subunidades. Basado en supuestos erróneos acerca de la localización de los hemas, optó por el equivocado para describir el oxigeno vinculante por la hemoglobina, asumiendo que la subunidad fue arreglada en un cuadrado. La ecuación a continuación proporciona la ecuación para una estructura tetraedral, que sería más precisa en el caso de la hemoglobina:

{bar {Y}}={frac {K[X]+3alpha {}K^{2}[X]^{2}+3alpha {}^{3}K^{3}[X]^{3}+alpha {}^{6}K^{4}[X]^{4}}{1+4K[X]+6alpha {}K^{2}[X]^{2}+4alpha {}^{3}K^{3}[X]^{3}+alpha {}^{6}K^{4}[X]^{4}}}

El modelo KNF

Basándose en los resultados que muestran que la estructura de las proteínas cooperativas cambió al unirse a su ligando, Daniel Koshland y sus colegas refinaron la explicación bioquímica del mecanismo descrito por Pauling. El modelo de Koshland-Némethy-Filmer (KNF) asume que cada subunidad puede existir en una de dos conformaciones: activa o inactiva. La unión del ligando a una subunidad induciría un cambio conformacional inmediato de esa subunidad de la conformación inactiva a la activa, un mecanismo descrito como "ajuste inducido". La cooperatividad, según el modelo KNF, surgiría de interacciones entre las subunidades, cuya fuerza varía dependiendo de las conformaciones relativas de las subunidades involucradas. Para una estructura tetraédrica (también consideraron estructuras lineales y cuadradas), propusieron la siguiente fórmula:

{bar {Y}}={frac {K_{{AB}}^{3}(K_{X}K_{t}[X])+3K_{{AB}}^{4}K_{{BB}}(K_{X}K_{t}[X])^{2}+3K_{{AB}}^{3}K_{{BB}}^{3}(K_{X}K_{t}[X])^{3}+K_{{BB}}^{6}(K_{X}K_{t}[X])^{4}}{1+4K_{{AB}}^{3}(K_{X}K_{t}[X])+6K_{{AB}}^{4}K_{{BB}}(K_{X}K_{t}[X])^{2}+4K_{{AB}}^{3}K_{{BB}}^{3}(K_{X}K_{t}[X])^{3}+K_{{BB}}^{6}(K_{X}K_{t}[X])^{4}}}

Donde $K_{X}$ es la constante de asociación para X, $K_{t}$ es la relación de B y A estados en ausencia de ligand ("transición"), $K_{{AB}}$ y $K_{{BB}}$ son las estabilidades relativas de pares de subunidades vecinas relativas a un par donde ambas subunidades están en el estado A (Nota que el papel KNF realmente presenta $N_s$ , el número de sitios ocupados, que está aquí 4 veces ${bar {Y}}$ ).

El modelo CMM

Monod-Wyman-Changeux esquema de reacción modelo de una proteína compuesta por dos protomers. El protomer puede existir bajo dos estados, cada uno con una afinidad diferente para el ligando. L es la proporción de estados en ausencia de ligand, c es la relación de afinidades.

Diagrama de energía de un modelo Monod-Wyman-Changeux de una proteína compuesta por dos protomers. La afinidad más grande del ligando para el estado R significa que este último está estabilizado preferentemente por la unión.

El modelo Monod-Wyman-Changeux (MWC) para transiciones alostéricas concertadas fue un paso más allá al explorar la cooperatividad basada en la termodinámica y las conformaciones tridimensionales. Originalmente se formuló para proteínas oligoméricas con subunidades idénticas dispuestas simétricamente, cada una de las cuales tiene un sitio de unión a ligando. Según este marco, dos (o más) estados conformacionales interconvertibles de una proteína alostérica coexisten en un equilibrio térmico. Los estados, a menudo denominados tenso (T) y relajado (R), difieren en la afinidad por la molécula del ligando. La relación entre los dos estados está regulada por la unión de moléculas de ligando que estabilizan el estado de mayor afinidad. Es importante destacar que todas las subunidades de una molécula cambian de estado al mismo tiempo, un fenómeno conocido como "transición concertada".

La constante de isomerización alosterica L describe el equilibrio entre ambos estados cuando ninguna molécula ligando está atada: $L={frac {left[T_{0}right]}{left[R_{0}right]}}$ . Si L es muy grande, la mayoría de la proteína existe en el estado T en ausencia de ligand. Si L es pequeño (cerca a uno), el estado R es casi tan poblado como el estado T. La relación de constantes de disociación para el ligando de los estados T y R se describe por la constante c: $c={frac {K_{d}^{R}}{K_{d}^{T}}}$ . Si $c=1$ , ambos estados R y T tienen la misma afinidad para el ligand y el ligand no afecta la isomerización. El valor de c también indica cuánto el equilibrio entre los estados T y R cambia sobre la unión ligando: el menor c, mientras más el equilibrio se desplaza hacia el estado R después de una unión. Con $alpha ={frac {[X]}{K_{d}^{R}}}$ , ocupación fraccional se describe como:

{bar {Y}}={frac {alpha (1+alpha)^{{n-1}}+Lcalpha (1+calpha)^{{n-1}}}{(1+alpha)^{n}+L(1+calpha)^{n}}}

El diagrama de Hill sigmoide de las proteínas alostéricas se puede analizar como una transición progresiva del estado T (baja afinidad) al estado R (alta afinidad) a medida que aumenta la saturación. La pendiente del Hill plot también depende de la saturación, con un valor máximo en el punto de inflexión. Las intersecciones entre las dos asíntotas y el eje y permiten determinar las afinidades de ambos estados por el ligando.

Hill plot of the MWC binding function in red, of the pure T and R state in green. A medida que la conformación cambia de T a R, también lo hace la función vinculante. Las interceptaciones con el eje x proporcionan la constante de disociación aparente, así como las constantes de disociación microscópica de los estados R y T.

En proteínas, el cambio conformacional se asocia con frecuencia con la actividad o la actividad hacia objetivos específicos. Tal actividad es a menudo lo que es fisiológicamente relevante o lo que se mide experimentalmente. El grado de cambio conformacional es descrito por la función estatal ${bar {R}}$ , que denota la fracción de proteína presente en la $R$ estado. Como ilustra el diagrama de energía, ${bar {R}}$ aumenta a medida que se unen más moléculas de ligando. La expresión ${bar {R}}$ es:

{bar {R}}={frac {(1+alpha)^{n}}{(1+alpha)^{n}+L(1+calpha)^{n}}}

Un aspecto crucial del modelo MWC es que las curvas ${bar {Y}}$ y ${bar {R}}$ no coinciden, es decir, la saturación fraccional no es un indicador directo de estado conformacional (y por lo tanto, de actividad). Además, las dimensiones de la cooperación de la unión y la cooperación de la activación pueden ser muy diferentes: un caso extremo es proporcionado por el motor bacteria flagella con un coeficiente Hill de 1.7 para la unión y 10.3 para la activación. La supra-linearidad de la respuesta se llama a veces ultrasensibilidad.

Si una proteína alostérica se une a un objetivo que también tiene una mayor afinidad por el estado R, la unión al objetivo estabiliza aún más el estado R y, por lo tanto, aumenta la afinidad del ligando. Si, por otro lado, un objetivo se une preferentemente al estado T, entonces la unión al objetivo tendrá un efecto negativo en la afinidad del ligando. Estos objetivos se denominan moduladores alostéricos.

Desde sus inicios, el marco del CMM se ha ampliado y generalizado. Se han propuesto variaciones, por ejemplo, para atender proteínas con más de dos estados, proteínas que se unen a varios tipos de ligandos o varios tipos de moduladores alostéricos y proteínas con subunidades o sitios de unión a ligandos no idénticos.

Ejemplos

La lista de ensamblajes moleculares que exhiben unión cooperativa de ligandos es muy grande, pero algunos ejemplos son particularmente notables por su interés histórico, sus propiedades inusuales o su importancia fisiológica.

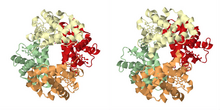
Representación de la hemoglobina de proteínas en sus dos conformaciones: "tensado (T)" en la izquierda correspondiente a la forma desoxidable (derivado de PDB id:11LFL) y "relajado (R)" en la derecha correspondiente a la forma oxi (derivado de PDB id:1LFT).

Como se describe en la sección histórica, el ejemplo más famoso de unión cooperativa es la hemoglobina. Su estructura cuaternaria, resuelta por Max Perutz mediante difracción de rayos X, exhibe un tetraedro pseudosimétrico que lleva cuatro sitios de unión (hemos) para el oxígeno. Se han estudiado con gran detalle muchos otros ensamblajes moleculares que exhiben unión cooperativa.

Enzimas multiméricas

La actividad de muchas enzimas está regulada por efectores alostéricos. Algunas de estas enzimas son multiméricas y llevan varios sitios de unión para los reguladores.

La treonina desaminasa fue una de las primeras enzimas sugeridas para comportarse como la hemoglobina y se demostró que se unía a los ligandos de manera cooperativa. Más tarde se demostró que era una proteína tetramérica.

Otra enzima que se sugirió anteriormente para unir ligandos de forma cooperativa es la aspartato trans-carbamilasa. Aunque los modelos iniciales eran consistentes con cuatro sitios de unión, William Lipscomb y sus colegas demostraron más tarde que su estructura era hexámera.

Canales iónicos

La mayoría de los canales iónicos están formados por varios monómeros o dominios idénticos o pseudoidénticos, dispuestos simétricamente en membranas biológicas. Varias clases de dichos canales cuya apertura está regulada por ligandos exhiben unión cooperativa de estos ligandos.

Ya en 1967 (cuando aún se desconocía la naturaleza exacta de esos canales) se sugirió que los receptores nicotínicos de acetilcolina se unían a la acetilcolina de manera cooperativa debido a la existencia de varios sitios de unión. La purificación del receptor y su caracterización demostraron una estructura pentamérica con sitios de unión ubicados en las interfases entre las subunidades, confirmado por la estructura del dominio de unión del receptor.

Los receptores de trifosfato de inositol (IP3) forman otra clase de canales iónicos activados por ligandos que muestran una unión cooperativa. La estructura de esos receptores muestra cuatro sitios de unión de IP3 dispuestos simétricamente.

Moléculas multisitio

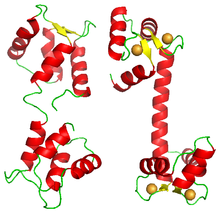
Aunque la mayoría de las proteínas que muestran unión cooperativa son complejos multiméricos de subunidades homólogas, algunas proteínas tienen varios sitios de unión para el mismo ligando en el mismo polipéptido. Un ejemplo de ello es la calmodulina. Una molécula de calmodulina se une cooperativamente a cuatro iones de calcio. Su estructura presenta cuatro dominios EF-hand, cada uno de los cuales se une a un ion de calcio. La molécula no muestra una estructura cuadrada o tetraédrica, sino que está formada por dos lóbulos, cada uno con dos dominios de mano EF.

Representación cartográfica de la proteína Calmodulina en su dos conformación: "cerrada" a la izquierda (derivada de PDB id: 1CFD) y "abierto" a la derecha (derivada de PDB id: 3CLN). La conformación abierta está representada ligada con 4 iones de calcio (esferas extrañas).

Factores de transcripción

También se ha demostrado la unión cooperativa de proteínas a ácidos nucleicos. Un ejemplo clásico es la unión del represor del fago lambda a sus operadores, que se produce de forma cooperativa. Otros ejemplos de factores de transcripción exhiben cooperatividad positiva al unirse a su diana, como el represor de las bombas TtgABC (n=1.6), así como cooperatividad condicional exhibida por los factores de transcripción HOXA11 y FOXO1.

Por el contrario, también se documentaron ejemplos de cooperatividad negativa para la unión de factores de transcripción, como para el represor homodimérico del operón hidroxilasa del citocromo P450cam de Pseudomonas putida (n=0,56).

Expansión conformacional y cooperatividad vinculante

Al principio, se ha argumentado que algunas proteínas, especialmente las que constan de muchas subunidades, podrían regularse mediante un mecanismo generalizado de MWC, en el que la transición entre el estado R y T no está necesariamente sincronizada en toda la proteína. En 1969, Wyman propuso un modelo de este tipo con "conformaciones mixtas" (es decir, algunos protómeros en estado R, algunos en estado T) para proteínas respiratorias en invertebrados.

Siguiendo una idea similar, el modelo de propagación conformacional de Duke y sus colegas subsume tanto el modelo KNF como el MWC como casos especiales. En este modelo, una subunidad no cambia automáticamente de conformación al unirse al ligando (como en el modelo KNF), ni todas las subunidades en un complejo cambian conformaciones juntas (como en el modelo MWC). Los cambios conformacionales son estocásticos con la probabilidad de que una subunidad cambie de estado dependiendo de si está o no unida al ligando y del estado conformacional de las subunidades vecinas. Por lo tanto, los estados conformacionales pueden "propagarse" alrededor de todo el complejo.

Impacto de los componentes aguas arriba y aguas abajo en la ultrasensibilidad del módulo

En una célula viva, los módulos ultrasensibles están integrados en una red más grande con componentes ascendentes y descendentes. Estos componentes pueden limitar el rango de entradas que recibirá el módulo, así como el rango de salidas del módulo que la red podrá detectar. La sensibilidad de un sistema modular se ve afectada por estas restricciones. Las limitaciones de rango dinámico impuestas por los componentes posteriores pueden producir sensibilidades efectivas mucho mayores que las del módulo original cuando se consideran de forma aislada.

Te puede interesar
Pirimidina
(leer más)
Te puede interesar
Ácido pirúvico
(leer más)
Te puede interesar
Roble
(leer más)
Más resultados...