Tronco

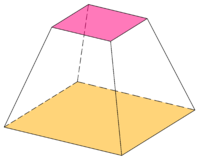
En geometría, un frustum (del latín 'bocado'; plural: frusta o frustums) es la parte de un sólido (normalmente una pirámide o un cono) que se encuentra entre dos planos paralelos que cortan este sólido. En el caso de una pirámide, las caras de la base son poligonales, las caras laterales son trapezoidales. Un tronco de árbol recto es una pirámide recta o un cono recto truncado perpendicularmente a su eje; de lo contrario, es un frustum oblicuo.

Si todas sus aristas son forzadas a tener la misma longitud, entonces un tronco se convierte en un prisma (posiblemente oblicuo y/o con bases irregulares).

En gráficos por computadora, el tronco de visualización es la región tridimensional que es visible en la pantalla. Está formado por una pirámide recortada; en particular, frustum culling es un método de determinación de superficie oculta.

En la industria aeroespacial, un tronco es el carenado entre dos etapas de un cohete de varias etapas (como el Saturno V), que tiene forma de cono truncado.

Elementos, casos especiales y conceptos relacionados

frusto cuadrado

Un octaedro regular se puede aumentar en 3 caras para crear un frusto triangular

El eje de un tronco es el del cono o pirámide original. Un tronco es circular si tiene bases circulares; es recto si el eje es perpendicular a ambas bases, y oblicuo en caso contrario.

La altura de un tronco es la distancia perpendicular entre los planos de las dos bases.

Los conos y las pirámides pueden verse como casos degenerados de frusta, donde uno de los planos de corte pasa por el vértice (de modo que la base correspondiente se reduce a un punto). Los troncos piramidales son una subclase de prismatoides.

Dos frusta con dos bases congruentes unidas en estas bases congruentes forman un bifrustum.

Fórmulas

Volumen

La fórmula para el volumen de un tronco piramidal cuadrado fue introducida por las matemáticas del antiguo Egipto en lo que se llama el Papiro Matemático de Moscú, escrito en la XIII dinastía (c.< span style="white-space:nowrap;"> 1850 aC):

${displaystyle V={frac}left(a^{2}+ab+b^{2}right),}$

donde a y b< /span> son las longitudes de la base y del lado superior, y h es la altura.

Los egipcios conocían la fórmula correcta para el volumen de una pirámide cuadrada truncada de este tipo, pero en el papiro de Moscú no se da ninguna prueba de esta ecuación.

El volumen de un tronco cónico o piramidal es el volumen del sólido antes de cortar su "ápice" apagado, menos el volumen de este "ápice":

${displaystyle V={frac {h_{1}B_{1}-h_{2} {3}}}}$

donde B₁ y B< sub>2 son las áreas base y superior, y h₁ y h₂ son las alturas perpendiculares desde el vértice hasta los planos base y superior.

Considerando que

${fnMicroc} {B_{1} {f}} {f}}} {f}}} {f}} {f}} {f}}} {f}}}}}} {f}}}}}} {f}}}}} {f}}}} {f}}}} {f}}} {f}}}}}}}}}}}}}}}}}}}}}}}} {\\f}}}}}}}}}}}}}}}}}}}}}} {\\\\\f}}}}}} {f}}}}}}}}} {f}}}} {f}} {f}}}} {f}} {f}}}}}} {f} {f} {f} {f} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {B_{2} {h_{2}}}={frac} {cHFF} {B_{1}}} {h_{1}h_{2}=alpha}} {cH}}}} {cH}}}}} {cH_}}}}} {cH}}}}}} {cH}} {}}}}}}}}} {}}}}}} {}}}}}} {}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {$

la fórmula para el volumen se puede expresar como el tercero del producto de esta proporcionalidad, ${displaystyle alpha }$, y de la diferencia de los cubos de las alturas h₁ y h₂ Sólo:

${displaystyle V={frac {h_{1}alpha {1} {2}-h_{2}alpha {fnMicroc} {fnMicroc} {fnMicroc} {fnK}}}} {fn}}} {fn}}}}\fnfnfn}fnfnfn\fnfnK}f}}\fnKfnK}}}}}}\\\\fn\\\\\\\fnK\\\fnKfnKfn\\\fnK\\fnK\fnK\\\\\fnK\\\\fnKfnK}fnh}\fnK\\fnK\fnK}\fn}\\\fn}fn}\\\\\fn}fn}\fn {h_{1}} {3} {3}}}} {3}}} {cH_}} {cH_} {cH_}} {cH_}}}}} {cH_}}}}} {cH_}}}} {ccH_}}}}} {cH_}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {cccccc}}}}}}}}}}}}}}}}}} {cccccccccccccccccccH_}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

Usando la identidad a³ − b³ = (a − b)(a² + ab + b²), se obtiene:

${displaystyle V=(h_{1}-h_{2}alpha {frac} {h_{1}} {2}}}}} {2}}}}} {2}} {3}}}}}$

donde h₁ − h₂ = h es la altura del tronco.

Distribución ${displaystyle alpha }$ y sustitución de su definición, la media heroniana de áreas B₁ y B₂ se obtiene:

${displaystyle {frac {B_{1}+{sqrt {B_{1}B_{2}}}+B_{2} {3}}}$

Por lo tanto, la fórmula alternativa es:

${displaystyle V={frac {h}{3}left(B_{1}+{sqrt ¿Qué?$

Heron of Alexandria se destaca por derivar esta fórmula y, con ella, encontrar la unidad imaginaria: la raíz cuadrada de uno negativo.

En particular:

• El volumen de un cono circular frustum es:

${displaystyle V={frac {fnMicroc} ¿Qué?$

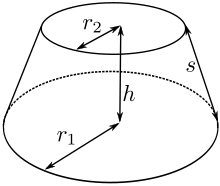
Donde r₁ y r₂ son la base y el radio superior.

• El volumen de un frusto piramidal cuyas bases son regulares n- es:

${displaystyle V={frac}left(a_{1}{2}+a_{1}a_{2}+a_{2}{2}{2}right)cot {fnMicroc} ♪♪$

Donde a₁ y a₂ son las longitudes laterales base y superior.

Superficie

frusto cónico

Modelo 3D de frusto cónico.

Para un tronco cónico circular recto

${displaystyle {begin{aligned}{text{Lateral surface area}} {=pipileft(r_{1}+r_{2}right)s\\\pileft(r_{1}+r_{2}right){sq} {sq} {}}}} {}} {}}}} {}}}}}}} {}}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}} {}}}}}}}}} {}}}}}} {}}}}}}}}}}}}}}}}} {}}} {}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}$

y

${2}} {2}}}} {2}}}}}}}i} {2}}i}}}i} {2}}}i}}i} {2}i}}}}}}i} {2}}}i}i} {2}}i}}}}}}i}}}}}\i}}}}}}}}}}}}\\\\2}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\]}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\\\]}}}}}}}}}}}}}}}}}$

donde r₁ y r₂ son los radios base y superior respectivamente, y s es la altura inclinada del tronco.

El área de superficie de un tronco de cono recto cuyas bases son polígonos regulares similares de n lados es

${displaystyle A={frac {n}{4}left [left(a_{1}{2}+a_{2}{2}right)cot {fnMicroc} ¿Qué? } {n}+4h^{2}left(a_{1}+a_{2}right)^{2}}}right]$

donde a₁ y a₂ son los lados de las dos bases.

Ejemplos

Los chocolates de la marca Rolo aproximan un frusto cónico circular derecho, aunque no plana en la parte superior.

• En la parte posterior (el reverso) de un proyecto de ley de un dólar de los Estados Unidos, un frusto piramidal aparece en el reverso del Gran Sello de los Estados Unidos, coronado por el Ojo de la Providencia.
• Ziggurats, pirámides escalonadas y algunos antiguos montículos nativos americanos también forman el frustum de una o más pirámides, con características adicionales como escaleras agregadas.
• pirámides chinas.
• El John Hancock Centro en Chicago, Illinois es un frustum cuyas bases son rectángulos.
• El Monumento de Washington es un estrecho frusto piramidal basado en cuadras rematado por una pequeña pirámide.
• El frustum visualizador en gráficos de computación 3D es un campo de visión virtual fotográfico o de videocámara modelado como un frusto piramidal.
• En la traducción al inglés de la colección de cuentos de Stanislaw Lem El Cyberiad, el poema Álgebra de amor y tensor afirma que "todo frustum anhela ser un cono".
• Los cubos y las típicas pantallas son ejemplos cotidianos de frustums cónicos.
• Beber vasos y algunas cápsulas espaciales también son algunos ejemplos.
• 

  Garsius Gaudyklė, Neringa, Lituania
  Estructura de madera o estatua de Garsulu Gaudyklė en Lituania.