Trisección de ángulo

Los ángulos pueden ser trisecados a través de una construcción de neusis utilizando herramientas más allá de una rectal sin marcar y una brújula. El ejemplo muestra la trisección de cualquier ángulo Рнели3π/4 por un gobernante con longitud igual al radio del círculo, dando ángulo trisecado φ=Silencio/3.

La trisección de ángulos es un problema clásico de construcción con regla y compás de las matemáticas griegas antiguas. Se trata de la construcción de un ángulo igual a un tercio de un ángulo arbitrario dado, usando solo dos herramientas: una regla sin marcar y un compás.

Pierre Wantzel demostró en 1837 que el problema, como se dijo, es imposible de resolver para ángulos arbitrarios. Sin embargo, aunque no hay forma de trisecar un ángulo en general con solo un compás y una regla, algunos ángulos especiales se pueden trisecar. Por ejemplo, es relativamente sencillo trisecar un ángulo recto (es decir, construir un ángulo de 30 grados).

Es posible trisecar un ángulo arbitrario utilizando otras herramientas además de la regla y el compás. Por ejemplo, la construcción de neusis, también conocida por los antiguos griegos, implica el deslizamiento y la rotación simultáneos de una regla marcada, lo que no se puede lograr con las herramientas originales. Otras técnicas fueron desarrolladas por matemáticos a lo largo de los siglos.

Debido a que se define en términos simples, pero complejos para demostrar que no tienen solución, el problema de la trisección de ángulos es un tema frecuente de intentos pseudomatemáticos de solución por parte de entusiastas ingenuos. Estas "soluciones" a menudo implican interpretaciones erróneas de las reglas, o simplemente son incorrectas.

Antecedentes y planteamiento del problema

La bisección de ángulos arbitrarios se ha resuelto desde hace mucho tiempo.

Usando solo una regla sin marcar y un compás, los matemáticos griegos encontraron medios para dividir una línea en un conjunto arbitrario de segmentos iguales, dibujar líneas paralelas, bisecar ángulos, construir muchos polígonos y construir cuadrados de igual o el doble de el área de un polígono dado.

Tres problemas resultaron difíciles de resolver, específicamente, trisecar el ángulo, duplicar el cubo y elevar al cuadrado el círculo. El problema de trisección de ángulos dice:

Construye un ángulo igual a un tercio de un ángulo arbitrario dado (o divídelo en tres ángulos iguales), usando solo dos herramientas:

1. una recta sin marcar, y
2. una brújula.

Prueba de imposibilidad

Reglas. Los mostrados están marcados: una recta ideal es sin marcar

Compases

Pierre Wantzel publicó una prueba de la imposibilidad de trisecar de forma clásica un ángulo arbitrario en 1837. La prueba de Wantzel, reformulada en terminología moderna, usa el concepto de extensiones de campo, un tema que ahora se combina típicamente con la teoría de Galois. Sin embargo, Wantzel publicó estos resultados antes que Évariste Galois (cuyo trabajo, escrito en 1830, se publicó recién en 1846) y no utilizó los conceptos introducidos por Galois.

El problema de construir un ángulo de una medida dada θ es equivalente a construir dos segmentos tales que la razón de sus longitudes sea cos θ. De una solución a uno de estos dos problemas, uno puede pasar a la solución del otro mediante una construcción con regla y compás. La fórmula del ángulo triple da una expresión que relaciona los cosenos del ángulo original y su trisección: cos θ = 4 cos³ θ/3 − 3 cos θ/3.

Se sigue que, dado un segmento que se define para tener una unidad de longitud, el problema de la trisección de un ángulo es equivalente a construir un segmento cuya longitud sea la raíz de un polinomio cúbico. Esta equivalencia reduce el problema geométrico original a un problema puramente algebraico.

Todo número racional es construible. Todo número irracional que se puede construir en un solo paso a partir de algunos números dados es una raíz de un polinomio de grado 2 con coeficientes en el campo generado por estos números. Por lo tanto, cualquier número que se pueda construir mediante una secuencia de pasos es una raíz de un polinomio mínimo cuyo grado es una potencia de dos. El ángulo π/3 radianes (60 grados, escrito 60°) es construible. El siguiente argumento muestra que es imposible construir un ángulo de 20°. Esto implica que un ángulo de 60° no puede trisecarse y, por lo tanto, un ángulo arbitrario no puede trisecarse.

Denote el conjunto de números racionales con Q. Si se pudiera trisecar 60°, el grado de un polinomio mínimo de cos 20° sobre Q sería una potencia de dos. Ahora sea x = cos 20°. Tenga en cuenta que cos 60° = cos π /3 = 1/2 . Luego, por la fórmula del triple ángulo, cos π/3 = 4x³ − 3x y así 4x³ − 3x = 1/2. Por lo tanto, 8x³ − 6x − 1 = 0. Defina p(t) como el polinomio p(t) = 8t³ − 6t − 1.

Dado que x = cos 20° es una raíz de p(t), el polinomio mínimo para cos 20° es un factor de p(t). Porque p(t) tiene grado 3, si es reducible por Q entonces tiene una raíz racional. Por el teorema de la raíz racional, esta raíz debe ser ±1, ±1/2, ±1/4 o ±1/8, pero ninguno de estos es una raíz. Por lo tanto, p(t) es irreducible por Q, y el polinomio mínimo para cos 20° es de grado 3.

Entonces un ángulo de medida 60° no se puede trisecar.

Ángulos que se pueden trisecar

Sin embargo, algunos ángulos se pueden trisecar. Por ejemplo, para cualquier ángulo construible θ, un ángulo de medida 3θ puede trisecarse de forma trivial ignorando el ángulo dado y construyendo directamente un ángulo de medida θ. Hay ángulos que no son construibles pero son trisectables (a pesar de que el ángulo de un tercio en sí mismo no es construible). Por ejemplo, 3π/7 es tal un ángulo: cinco ángulos de medida 3π/7 se combinan para formar un ángulo de medida 15π/7 , que es un círculo completo más el π/7.

Para un entero positivo N, un ángulo de medida 2π/N es trisecable si y solo si 3 no divide N. Por el contrario, 2π/N es construible si y solo si N es una potencia de 2 o el producto de una potencia de 2 con el producto de uno o más números primos de Fermat distintos.

Caracterización algebraica

De nuevo, denote el conjunto de números racionales con Q.

Teorema: Un ángulo de medida θ puede ser trisecado si y solo si q(t) = 4t³ − 3t − cos(θ) es reducible sobre la extensión de campo Q(cos(θ)).

La prueba es una generalización relativamente directa de la prueba anterior de que un ángulo de 60° no es trisecable.

Otras cantidades de piezas

Para cualquier entero distinto de cero N, un ángulo de medida 2π⁄N Los radianes se pueden dividir en n partes iguales con regla y compás si y solo si n es una potencia de 2 o es una potencia de 2 multiplicada por el producto de uno o más números primos de Fermat distintos, ninguno de los cuales divide N. En el caso de la trisección (n = 3, que es un primo de Fermat), esta condición se convierte en el requisito antes mencionado de que N no sea divisible por 3.

Otros métodos

El problema general de la trisección de ángulos se puede resolver usando herramientas adicionales y, por lo tanto, saliendo del marco griego original de compás y regla.

Se han propuesto muchos métodos incorrectos para trisectar el ángulo general. Algunos de estos métodos proporcionan aproximaciones razonables; otros (algunos de los cuales se mencionan a continuación) involucran herramientas no permitidas en el problema clásico. El matemático Underwood Dudley ha detallado algunos de estos intentos fallidos en su libro The Trisectors.

Aproximación por bisecciones sucesivas

La trisección se puede aproximar mediante la repetición del método del compás y la regla para bisecar un ángulo. La serie geométrica 1/3 = 1/4 + 1/16 + 1/64 + 1/256 + ⋯ o 1/3 = 1/2 − 1/4 + 1/8 − 1/16 + ⋯ se puede utilizar como base para las bisecciones. Se puede obtener una aproximación con cualquier grado de precisión en un número finito de pasos.

Usando papiroflexia

La trisección, como muchas construcciones imposibles con regla y compás, se puede lograr fácilmente mediante operaciones de plegado de papel u origami. Los axiomas de Huzita (tipos de operaciones de plegado) pueden construir extensiones cúbicas (raíces cúbicas) de longitudes dadas, mientras que la regla y el compás solo pueden construir extensiones cuadráticas (raíces cuadradas).

Usando un vínculo

Abanicos de Enlace de Sylvester

Hay una serie de enlaces simples que se pueden usar para hacer un instrumento para trisecar ángulos, incluido el trisector de Kempe y el ventilador de enlace de Sylvester o el isoklinostat.

Con una regla triangular recta

La trisección de Bieberbach de un ángulo (en azul) por medio de un gobernante triangular derecho (en rojo)

En 1932, Ludwig Bieberbach publicó en Journal für die reine und angewandte Mathematik su obra Zur Lehre von den kubischen Konstruktionen. Dice en él (traducción libre):

"Como se sabe... cada construcción cúbica se puede rastrear de nuevo a la trisección del ángulo y a la multiplicación del cubo, es decir, la extracción de la tercera raíz. Sólo necesito mostrar cómo estas dos tareas clásicas se pueden resolver por medio del gancho ángulo recto."

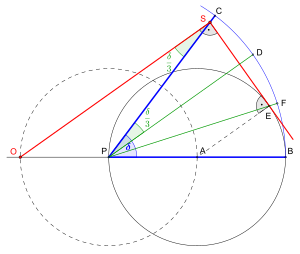
La construcción comienza dibujando un círculo que pasa por el vértice P del ángulo a trisecar, centrado en A en un borde de este ángulo, y que tiene B como su segunda intersección con el borde. Un círculo con centro en P y del mismo radio corta la línea que sostiene el borde en A y O.

Ahora la regla triangular recta se coloca en el dibujo de la siguiente manera: un cateto de su ángulo recto pasa a través de O; el vértice de su ángulo recto se coloca en un punto S de la línea PC de tal manera que el segundo tramo de la regla sea tangente en E al círculo centrado en A. Se sigue que el ángulo original es trisecado por la línea PE, y la línea PD perpendicular a SE y pasando por P. Esta línea se puede trazar usando nuevamente la regla triangular derecha o usando una regla tradicional y una construcción de compás. Con una construcción similar, se puede mejorar la ubicación de E, usando que es la intersección de la línea SE y su perpendicular pasando por A.

Prueba: Uno tiene que demostrar la igualdad de ángulo EPD^ ^ =DPS^ ^ {displaystyle {widehat {}={widehat {DPS}}} y BPE^ ^ =EPD^ ^ .{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} Las tres líneas OS, PD, y AE son paralelos. Como segmentos de línea OP y PA son iguales, estas tres líneas paralelas delimitan dos segmentos iguales en cada otra línea de secant, y en particular en su perpendicular común SE. Así SD' = D'E, donde D ' es la intersección de las líneas PD y SE. Sigue que los triángulos derecho PD'S y PD'E son congruentes, y así EPD^ ^ =DPS^ ^ ,{displaystyle {widehat {}={widehat {DPS}}} la primera igualdad deseada. Por otro lado, el triángulo PAE es isosceles, ya que todos los radios de un círculo son iguales; esto implica que APE^ ^ =AEP^ ^ .{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} Uno también tiene AEP^ ^ =EPD^ ^ ,{displaystyle {widehat {}={widehat {EPD}}} ya que estos dos ángulos son ángulos alternativos de una línea transversal a dos líneas paralelas. Esto demuestra la segunda igualdad deseada, y así la corrección de la construcción.

Con una curva auxiliar

• 

  Trisección usando la espiral arquímica

• 

  Trisección usando el trisectrix de Maclaurin

Hay ciertas curvas llamadas trisectrices que, si se dibujan en el plano usando otros métodos, se pueden usar para trisecar ángulos arbitrarios. Los ejemplos incluyen la trisectriz de Colin Maclaurin, dada en coordenadas cartesianas por la ecuación implícita

2x()x2+Sí.2)=a()3x2− − Sí.2),{displaystyle 2x(x^{2}+y^{2})=a(3x^{2}-y^{2}

y la espiral de Arquímedes. De hecho, la espiral se puede usar para dividir un ángulo en cualquier número de partes iguales. Arquímedes describió cómo trisecar un ángulo usando la espiral de Arquímedes en On Spirals alrededor del 225 a.

Con una regla marcada

Trisección del ángulo mediante regla marcada

Otra forma de trisecar un ángulo arbitrario por un "pequeño" El paso fuera del marco griego es a través de una regla con dos marcas separadas por una distancia determinada. La siguiente construcción se debe originalmente a Arquímedes, llamada construcción de Neusis, es decir, que utiliza herramientas distintas a una regla sin marcar. Los diagramas que usamos muestran esta construcción para un ángulo agudo, pero de hecho funciona para cualquier ángulo hasta 180 grados.

Esto requiere tres hechos de la geometría (a la derecha):

1. Cualquier conjunto completo de ángulos en línea recta añadir a 180°,
2. La suma de ángulos de cualquier triángulo es de 180°, y,
3. Cualquier dos lados iguales de un triángulo isosceles se reunirá con el tercer lado en el mismo ángulo.

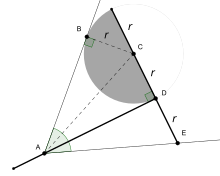
Sea l la línea horizontal en el diagrama adyacente. Ángulo a (a la izquierda del punto B) es el tema de la trisección. Primero, se dibuja un punto A en el rayo de un ángulo, una unidad aparte de B. Se dibuja un círculo de radio AB. Luego, la marca de la regla entra en juego: una marca de la regla se coloca en A y la otra en B. Mientras mantiene la regla (pero no la marca) tocando A, la regla se desliza y gira hasta que una marca está en el círculo y el otro está en la línea l. La marca en el círculo tiene la etiqueta C y la marca en la línea tiene la etiqueta D. Esto asegura que CD = AB. Se dibuja un radio BC para que sea obvio que los segmentos de línea AB, BC y CD todos tienen la misma longitud. Ahora, los triángulos ABC y BCD son isósceles, por lo tanto (por el Hecho 3 anterior) cada uno tiene dos ángulos iguales.

Hipótesis: Dada AD es una línea recta, y AB, BC y CD todos tienen la misma longitud,

Conclusión: ángulo b = a/3.

Prueba:

1. De hecho 1) arriba, e+c=180{displaystyle e+c=180}°.
2. Mirando el triángulo BCD, de hecho 2) e+2b=180{displaystyle e+2b=180}°.
3. De las dos últimas ecuaciones, c=2b{displaystyle c=2b}.
4. De hecho 2), d+2c=180{displaystyle d+2c=180}°, así d=180{displaystyle d=180}°− − 2c{displaystyle -2c}Así que desde el último, d=180{displaystyle d=180}°− − 4b{displaystyle -4b..
5. De hecho 1) arriba, a+d+b=180{displaystyle a+d+b=180}°, así a+()180{displaystyle a+(180)°− − 4b)+b=180{displaystyle -4b)+b=180}°.

Limpieza, a − 3b = 0, o a = 3b, y el teorema queda demostrado.

Nuevamente, esta construcción salió del marco de las construcciones permitidas al usar una regla marcada.

Con una cuerda

Thomas Hutcheson publicó un artículo en el Mathematics Teacher que usaba una cuerda en lugar de un compás y una regla. Una cuerda puede usarse como una regla (estirándola) o como un compás (fijando un punto e identificando otro), pero también puede enrollarse alrededor de un cilindro, la clave de la solución de Hutcheson.

Hutcheson construyó un cilindro a partir del ángulo a trisecar dibujando un arco a través del ángulo, completándolo como un círculo y construyendo a partir de ese círculo un cilindro en el que se inscribió, digamos, un triángulo equilátero (un ángulo de 360 grados dividido en tres). Esto fue luego "mapeado" sobre el ángulo a trisecar, con una prueba simple de triángulos semejantes.

Con un "tomahawk"

Un tomahawk recortando un ángulo. El tomahawk está formado por las líneas gruesas y el semicírculo sombreado.

Un "tomahawk" es una forma geométrica que consta de un semicírculo y dos segmentos de línea ortogonales, de modo que la longitud del segmento más corto es igual al radio del círculo. La trisección se ejecuta inclinando el extremo del segmento más corto del tomahawk en un rayo, el borde del círculo en el otro, de modo que el "mango" (segmento más largo) cruza el vértice del ángulo; la línea de trisección corre entre el vértice y el centro del semicírculo.

Si bien un tomahawk se puede construir con compás y regla, generalmente no es posible construir un tomahawk en la posición deseada. Por lo tanto, la construcción anterior no contradice la no trisectibilidad de los ángulos solo con regla y compás.

Dado que un tomahawk se puede usar como escuadra, también se puede usar para ángulos de trisección mediante el método descrito en § Con una regla triangular recta.

El tomahawk produce el mismo efecto geométrico que el método de plegado de papel: la distancia entre el centro del círculo y la punta del segmento más corto es el doble de la distancia del radio, lo que garantiza que haga contacto con el ángulo. También es equivalente al uso de una regla L de arquitectos (Carpenter's Square).

Con brújulas interconectadas

Se puede trisecar un ángulo con un dispositivo que es esencialmente una versión de cuatro puntas de una brújula, con conexiones entre las puntas diseñadas para mantener iguales los tres ángulos entre puntas adyacentes.

Usos de la trisección de ángulos

Una animación de una construcción neusis de un heptógono con radio de circuncircle OĀ ̄ =6{displaystyle {fnK}=6}, basado en Andrew M. Gleason, utilizando trisección de ángulo por medio del tomahawk

Una ecuación cúbica con coeficientes reales se puede resolver geométricamente con compás, regla y una trisectriz angular si y solo si tiene tres raíces reales.

Un polígono regular con n los lados se pueden construir con regla, brújula y trisector de ángulo si y sólo si n=2r3sp1p2⋯ ⋯ pk,{displaystyle ## #2# {r}3^{1}p_{2}cdots P_{k},} Donde r, s, k ≥ 0 y dónde p_i son primas diferentes superior a 3 de la forma 2t3u+1{displaystyle 2^{t}3^{u}+1} (es decir, Pierpont primas superiores a 3).