Triple pitagórico
Un triple pitagórico consta de tres números enteros positivos a, b, y c, tal que a 2 + b2 = c2. Tal triple se escribe comúnmente (a, b, c), y un pozo -un ejemplo conocido es (3, 4, 5). Si (a, b, c) es una terna pitagórica, entonces también lo es (ka, kb, kc) para cualquier entero positivo <span class="texhtml" k. Una terna pitagórica primitiva es aquella en la que a, b y c son coprimos (es decir, no tienen un divisor común mayor que 1). Por ejemplo, (3, 4, 5) es un triple pitagórico primitivo mientras que (6, 8, 10) no lo es. Un triángulo cuyos lados forman una terna pitagórica se llama triángulo pitagórico, y es necesariamente un triángulo rectángulo.
El nombre se deriva del teorema pitagórico, indicando que cada triángulo derecho tiene longitudes laterales que satisfacen la fórmula a2+b2=c2{displaystyle a^{2}+b^{2}=c^{2}; por lo tanto, los triples pitagóricos describen las tres longitudes del lado entero de un triángulo derecho. Sin embargo, los triángulos rectos con los lados no enteros no forman los triples pitagóricos. Por ejemplo, el triángulo con los lados a=b=1{displaystyle a=b=1} y c=2{displaystyle c={sqrt {2}} es un triángulo derecho, pero ()1,1,2){displaystyle (1,1,{sqrt {2}}} no es un triple pitagórico porque 2{displaystyle {sqrt {2}} no es un entero. Además, 1{displaystyle 1} y 2{displaystyle {sqrt {2}} no tiene un integer común múltiple porque 2{displaystyle {sqrt {2}} es irracional.
Las ternas pitagóricas se conocen desde la antigüedad. El registro más antiguo conocido proviene de Plimpton 322, una tablilla de arcilla babilónica de alrededor de 1800 a. C., escrita en un sistema numérico sexagesimal. Fue descubierto por Edgar James Banks poco después de 1900 y vendido a George Arthur Plimpton en 1922 por 10 dólares.
Al buscar soluciones enteras, la ecuación a2 + b2 = c2 es una ecuación diofántica. Así, las ternas pitagóricas se encuentran entre las soluciones conocidas más antiguas de una ecuación diofantiana no lineal.
Ejemplos
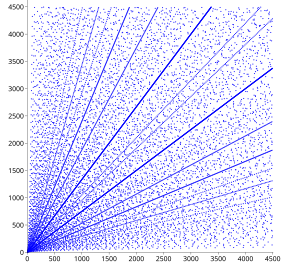
Hay 16 ternas pitagóricas primitivas de números hasta 100:
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
Otras pequeñas ternas pitagóricas como (6, 8, 10) no se enumeran porque no son primitivas; por ejemplo (6, 8, 10) es un múltiplo de (3, 4, 5).
Cada uno de estos puntos (con sus múltiplos) forma una línea radiante en el gráfico de dispersión de la derecha.
Además, estos son los restantes triples pitagóricos primitivos de números hasta 300:
| (20, 99, 101) | (60, 91, 109) | (15, 112, 113) | (44, 117, 125) |
| (88, 105, 137) | (17, 144, 145) | (24, 143, 145) | (51, 140, 149) |
| (85, 132, 157) | (119, 120, 169) | (52, 165, 173) | (19, 180, 181) |
| (57, 176, 185) | (104, 153, 185) | (95, 168, 193) | (28, 195, 197) |
| (84, 187, 205) | (133, 156, 205) | (21, 220, 221) | (140, 171, 221) |
| (60, 221, 229) | (105, 208, 233) | (120, 209, 241) | (32, 255, 257) |
| (23, 264, 265) | (96, 247, 265) | (69, 260, 269) | (115, 252, 277) |
| (160, 231, 281) | (161, 240, 289) | (68, 285, 293) |
Generando un triple
La fórmula de Euclides es una fórmula fundamental para generar ternas pitagóricas dado un par arbitrario de números enteros m y n con m > n > 0. La fórmula establece que los números enteros
- a=m2− − n2,b=2mn,c=m2+n2{displaystyle a=m^{2}-n^{2},\,b=2mn, ,c=m^{2}+n^{2}}
formar una terna pitagórica. El triple generado por la fórmula de Euclides es primitivo si y solo si m y n son coprimos y uno de ellos es par. Cuando tanto m como n son impares, entonces a, b y c será par, y el triple no será primitivo; sin embargo, dividir a, b y c por 2 generará un triple primitivo cuando m y n son coprimos.
Toda terna primitiva surge (después del intercambio de a y b, si a es par) de un par único de números coprimos m, n, uno de los cuales es par. De ello se deduce que hay infinitas ternas pitagóricas primitivas. Esta relación de a, b y c a m y n de la fórmula de Euclides se menciona en el resto de este artículo.
A pesar de generar todos los triples primitivos, la fórmula de Euclides no produce todos los triples; por ejemplo, (9, 12, 15) no se puede generar usando el número entero m y n. Esto se puede remediar insertando un parámetro adicional k en la fórmula. Lo siguiente generará todos los triples pitagóricos de forma única:
- a=k⋅ ⋅ ()m2− − n2),b=k⋅ ⋅ ()2mn),c=k⋅ ⋅ ()m2+n2){displaystyle a=kcdot (m^{2}-n^{2}), ,b=kcdot (2mn), ,c=kcdot (m^{2}+n^{2}}}
donde m, n y k son números enteros positivos con m > n, y con m y n coprimos y no ambos impares.
Que estas fórmulas generan ternas pitagóricas se puede verificar expandiendo a2 + b 2 usando álgebra elemental y verificando que el resultado es igual a c2. Dado que cada triple pitagórico se puede dividir por algún número entero k para obtener un triple primitivo, cada triple se puede generar de forma única usando la fórmula con m y n para generar su homólogo primitivo y luego multiplicar por k como en la última ecuación.
Elegir m y n de ciertas secuencias enteras da resultados interesantes. Por ejemplo, si m y n son números Pell consecutivos, a y b diferirán en 1.
Se han desarrollado muchas fórmulas para generar triples con propiedades particulares desde la época de Euclides.
Prueba de la fórmula de Euclides
Que la satisfacción de la fórmula de Euclides por a, b, c es suficiente para que el triángulo sea pitagórico es evidente por el hecho de que para los números enteros positivos m y n, m > n, a, b y c dados por la fórmula son todos números enteros positivos, y por el hecho de que
- a2+b2=()m2− − n2)2+()2mn)2=()m2+n2)2=c2.{displaystyle a^{2}+b^{2}=(m^{2}-n^{2})^{2}+(2mn)^{2}=(m^{2}+n^{2})^{2}=c^{2}}}}}}}
Una prueba de la necesidad de que a, b, c se expresen mediante la fórmula de Euclides para cualquier terna pitagórica primitiva es la siguiente. Todos estos triples primitivos se pueden escribir como (a, b, c) donde a2 + b2 = c2 y a, b, c son coprimos. Así a, b, c son coprimos por pares (si un número primo dividiera a dos de ellos, estaría obligado a dividir también al tercero). Como a y b son coprimos, al menos uno de ellos es impar, por lo que podemos suponer que a es impar, intercambiando, si es necesario, a y b. Esto implica que b es par y c es impar (si b fueran impares, c serían pares y c2 sería un múltiplo de 4, mientras que a 2 + b2 serían congruentes con 2 módulo 4, como un cuadrado impar es congruente con 1 módulo 4).
Desde a2+b2=c2{displaystyle a^{2}+b^{2}=c^{2} obtenemos c2− − a2=b2{displaystyle C^{2}-a^{2}=b^{2} y por consiguiente ()c− − a)()c+a)=b2{displaystyle (c-a)(c+a)=b^{2}. Entonces... ()c+a)b=b()c− − a){displaystyle {tfrac {}{b}={tfrac} {b}{(c-a)}}}. Desde ()c+a)b{displaystyle {tfrac {(c+a)}{b}} es racional, lo fijamos igual a mn{fnMicroc} {m} {n}} en términos más bajos. Así ()c− − a)b=nm{displaystyle {tfrac}{b}={tfrac {n} {m}}, siendo el recíproco de ()c+a)b{displaystyle {tfrac {(c+a)}{b}}. Entonces resolviendo
- cb+ab=mn,cb− − ab=nm{fnMicroc} {c}{b}+{frac} {a}{b}={frac} {m}{n},quad quad {frac} {c}{b}-{frac} {a}{b}={frac} {n} {m}}
para cb{fnMicroc} {c}{b}} y ab{displaystyle {tfrac {}{b}} da
- cb=12()mn+nm)=m2+n22mn,ab=12()mn− − nm)=m2− − n22mn.{fnMicroc} {c}{b}={frac} {1}{2}left({frac} {m}{n}+{frac} {n} {m}right)={frac {m^{2}+n^{2mn}}quad quad {frac {a}{b}={frac} {1}{2}left({frac} {m} {n}-{frac} {n} {m}right)={frac {m^{2}-n^{2mn}}}
As mn{fnMicroc} {m} {n}} se reduce plenamente, m y n son coprime, y no pueden ser ambos. Si ambos eran extraños, el numerador de m2− − n22mn{fnMicroc} {m^{2}-n^{2mn}} sería un múltiplo de 4 (porque un cuadrado extraño es congruente con 1 modulo 4), y el denominador 2mn no sería un múltiple de 4. Puesto que 4 sería el factor mínimo posible incluso en el numerador y 2 sería el factor máximo posible incluso en el denominador, esto implicaría a ser incluso a pesar de definirlo como extraño. Así uno de m y n es extraño y el otro es incluso, y los numeradores de las dos fracciones con denominador 2mn son extraños. Así estas fracciones se reducen completamente (una prima rara que divide este denominador divide uno de m y n pero no el otro; así no se divide m2 ± n2). Uno puede equiparar a numeradores con numeradores y denominadores con denominadores, dando la fórmula de Euclid
- a=m2− − n2,b=2mn,c=m2+n2{displaystyle a=m^{2}-n^{2},\,b=2mn, ,c=m^{2}+n^{2}} con m y n coprime y de paridades opuestas.
Maor (2007) y Sierpiński (2003) ofrecen una prueba más larga pero más común. Otra prueba se da en la ecuación diofántica § Ejemplo de ternas pitagóricas, como ejemplo de un método general que se aplica a toda ecuación diofántica homogénea de grado dos.
Interpretación de parámetros en la fórmula de Euclides
Suponga que los lados de un triángulo pitagórico tienen longitudes m2 − n2, 2mn, y m2 + n2, y suponer el ángulo entre la pierna de longitud m2 − n2 y la hipotenusa de la longitud m2 + n2 es denotado como β. Entonces... # β β 2=nm{displaystyle tan {tfrac {beta } {2}={tfrac {n} {m}} y los valores trigonométricos completos son pecado β β =2mnm2+n2{displaystyle sin {beta }={tfrac {2mn}{m^{2}+n^{2}}}, # β β =m2− − n2m2+n2{displaystyle cos {beta }={tfrac {m^{2}-n^{2} {m^{2}, y # β β =2mnm2− − n2{displaystyle tan {beta }={tfrac {2mn}{m^{2}-n^{2}}}.
Una variante
La siguiente variante de la fórmula de Euclides a veces es más conveniente, ya que es más simétrica en m y n (misma condición de paridad en m y n).
Si m y n son dos enteros impares tales que m > n, entonces
- a=mn,b=m2− − n22,c=m2+n22{displaystyle a=mn,\fnMicrosoft Sans {m^{2}-n^{2}}{2}}\,c={frac} {m^{2}+n^{2}} {2}}}}
son tres números enteros que forman una terna pitagórica, que es primitiva si y solo si m y n son coprimos. Por el contrario, cada terna pitagórica primitiva surge (después del intercambio de a y b, si a es par) de un par único m > n > 0 de enteros impares coprimos.
Propiedades elementales de las ternas pitagóricas primitivas
Propiedades generales
Las propiedades de una terna pitagórica primitiva (a, b, c) con a < b < c (sin especificar cuál de a o b es par y cuál es impar) incluyen:
- ()c− − a)()c− − b)2{displaystyle {tfrac {(c-a)(c-b)}{2}} es siempre un cuadrado perfecto. Como es sólo una condición necesaria pero no una suficiente, se puede utilizar en la comprobación si un triple dado de números es no a Pythagorean triple cuando fallan la prueba. Por ejemplo, los triples {6, 12, 18} y {1, 8, 9} cada uno pasa la prueba que ()c − a)c − b)/2 es un cuadrado perfecto, pero tampoco es un triple pitagórico.
- Cuando un triple de números a, b y c forma un primitivo Pythagorean triple, entonces ()c menos la pierna) y mitad de ()c menos la pierna extraña) son los dos cuadrados perfectos; sin embargo esto no es una condición suficiente, como los números {1, 8, 9} pasar la prueba de cuadrados perfectos pero no son un triple pitagórico desde 12 + 82 ل 92.
- En la mayoría de uno a, b, c es un cuadrado.
- El área de un triángulo pitagórico no puede ser el cuadrado o dos veces el cuadrado de un número natural.
- Exactamente uno de a, b es divisible por 2 (es incluso), pero nunca c.
- Exactamente uno de a, b es divisible por 3, pero nunca c.
- Exactamente uno de a, b es divisible por 4, pero nunca c (porque c nunca es ni siquiera).
- Exactamente uno de a, b, c es divisible por 5.
- El mayor número que siempre divide abc es 60.
- Cualquier número extraño de la forma 2m+ 1, donde m es un entero y m■ 1, puede ser la pierna extraña de un triple pitagórico primitivo [PPT]. Ver la sección PPT de casi isósceles a continuación. Sin embargo, sólo los números divisibles por 4 pueden ser incluso la pierna de un PPT. Esto es porque la fórmula de Euclid para la pierna incluso dada arriba es 2mn y uno de m o n Debe ser igual.
- La hipotenusa c es la suma de dos cuadrados. Esto requiere que todos sus factores principales sean los primeros de la forma 4n + 1. Por lo tanto, c es de la forma 4n + 1. Una secuencia de posibles números de hipotenusa para un PPT se puede encontrar en (secuencia A008846 en el OEIS).
- La zona ()K = ab/2) es un número congruente divisible por 6.
- En cada triángulo pitagórico, el radio del incircle y los radios de los tres excircles son números naturales. Específicamente, para un triple primitivo el radio del círculo es r = n()m − n), y el radio de los excircos frente a los lados m2 − n2, 2mn, y la hipotenusa m2 + n2 respectivamente m()m − n), n()m + n), y m()m + n).
- En cuanto a cualquier triángulo derecho, el converso del teorema de Thales dice que el diámetro del círculo equivale a la hipotenusa; por lo tanto, para los primitivos triples el circundiametro es m2 + n2, y el circunradius es la mitad de esto y por lo tanto es racional pero no-integer (desde m y n tienen paridad opuesta).
- Cuando el área de un triángulo pitagórico se multiplica por las curvaturas de su incircle y 3 excircles, el resultado es cuatro enteros positivos w ■ x ■ Sí. ■ z, respectivamente. Integers −w, x, Sí., z satisfacer la ecuación del círculo de Descartes. Equivalentemente, el radio del círculo exterior del Soddy de cualquier triángulo derecho es igual a su semiperímetro. El centro exterior de Soddy está situado en D, donde ACBD es un rectángulo, ACB el triángulo derecho y AB su hipotenusa.
- Sólo dos lados de un triple pitagórico primitivo pueden ser simultáneamente primeros porque por la fórmula de Euclid para generar un triple pitagórico primitivo, una de las piernas debe ser compuesta e incluso. Sin embargo, sólo un lado puede ser un entero de poder perfecto p≥ ≥ 2{displaystyle pgeq 2} porque si dos lados eran enteros de poderes perfectos con igual exponente p{displaystyle p} contradice el hecho de que no hay soluciones enteros a la ecuación Diofantina x2p± ± Sí.2p=z2{displaystyle x^{2p}pm ¿Qué?, con x{displaystyle x}, Sí.{displaystyle y} y z{displaystyle z} ser pareado coprime.
- No hay triángulos pitagóricos en los que la hipotenusa y una pierna son las piernas de otro triángulo pitagórico; esta es una de las formas equivalentes del teorema triángulo derecho de Fermat.
- Cada primitivo El triángulo pitagórico tiene una relación de área, K, a semiperímetro cuadrado, s, que es único a sí mismo y es dado por
- Ks2=n()m− − n)m()m+n)=1− − cs.{displaystyle {frac {K}{2}}={frac {n(m-n)}{m(m+n)}}=1-{frac {c}{s}}
- Ningún triángulo pitagórico primitivo tiene una altitud entero de la hipotenusa; es decir, cada triángulo pitagórico primitivo es indecomposible.
- El conjunto de todos los primitivos triples pitagóricos forma un árbol ternario arraigado de manera natural; vea Árbol de los primitivos triples pitagóricos.
- Ninguno de los ángulos agudos de un triángulo pitagórico puede ser un número racional de grados. (Esto sigue del teorema de Niven.)
Casos especiales
Además, se puede garantizar la existencia de ternas pitagóricas especiales con ciertas propiedades adicionales:
- Cada entero mayor que 2 que no es congruente con 2 mod 4 (en otras palabras, cada entero mayor que 2 que es no de la forma 4k + 2) es parte de un triple pitagórico primitivo. (Si el entero tiene la forma 4k, uno puede tomar n = 1 y m = 2k en la fórmula de Euclid; si el entero es 2k + 1, uno puede tomar n = k y m = k + 1.)
- Cada entero mayor de 2 es parte de un triple pitagórico primitivo o no primario. Por ejemplo, los enteros 6, 10, 14, y 18 no forman parte de los triples primitivos, sino que forman parte de los triples no primarios (6, 8, 10), (14, 48, 50) y (18, 80, 82).
- Existen infinitamente muchos triples pitagóricos en los que la hipotenusa y la pierna más larga difieren exactamente por uno. Tales triples son necesariamente primitivos y tienen la forma (22)n + 1, 2n2 + 2n, 2n2 + 2n +1). Esto resulta de la fórmula de Euclid señalando que la condición implica que el triple es primitivo y debe verificar ()m2 + n2- 2mn = 1. Esto implica ()m – n)2 = 1, y así m = n + 1. La forma anterior de los triples resultados así de sustitución m para n + 1 en la fórmula de Euclid.
- Existen infinitamente muchos primitivos triples pitagóricos en los que la hipotenusa y la pierna más larga difieren exactamente por dos. Todos son primitivos, y se obtienen poniendo n = 1 en la fórmula de Euclid. Más generalmente, por cada entero k ■ 0, existen infinitamente muchos primitivos triples pitagóricos en los que la hipotenusa y la pierna extraña difieren 2k2. Se obtienen poniendo n = k en la fórmula de Euclid.
- Existen infinitamente muchos triples pitagóricos en los que las dos piernas difieren exactamente por una. Por ejemplo, 202 + 212 = 292; estos son generados por la fórmula de Euclid cuando m− − nn{fnMicroc} {m-n}{n}} es una convergencia 2{displaystyle {sqrt {2}}.
- Para cada número natural k, existen k Pythagorean triples con diferentes hipotentas y la misma área.
- Para cada número natural k, hay al menos k diferentes primitivos Pythagorean triples con la misma pierna a, donde a es un número natural (la longitud de la pierna es 2mn, y basta elegir a con muchas factorizaciones, por ejemplo a = 4b, donde b es un producto de k diferentes primas extrañas; esto produce al menos 2k diferentes triples primitivos).
- Para cada número natural k, hay al menos k diferentes Pythagorean triples con la misma hipotenusa.
- Si c = pe es un poder primitivo, existe un triple pitagórico primitivo a2 + b2 = c2 si y sólo si la primera p tiene la forma 4n + 1; este triple es único hasta el intercambio de a y b.
- Más generalmente, un entero positivo c es la hipotenusa de un primitivo Pythagorean triple si y sólo si cada factor principal de c es congruente con 1 modulo 4; es decir, cada factor principal tiene la forma 4n + 1. En este caso, el número de trillizos pitagóricos primitivos ()a, b, c) con a. b es 2k−1, donde k es el número de factores principales distintos c.
- Existen infinitamente muchos triples pitagóricos con números cuadrados para ambos la hipotenusa c y la suma de las piernas a + b. Según Fermat, el más pequeña tal triple tiene lados a = 4,565,486,027.761; b = 1,061,652,293,520; y c = 4.687.298.610.289. Aquí. a + b = 2,372,1592 y c = 2.165.0172. Esto es generado por la fórmula de Euclid con valores de parámetro m = 2.150.905 y n = 246,792.
- Existen triángulos pitagóricos no primarios con altitud de entero de la hipotenusa. Tales triángulos pitagóricos son conocidos como descompuesto ya que pueden dividirse a lo largo de esta altitud en dos triángulos Pythagorean separados y más pequeños.
Geometría de la fórmula de Euclides
Puntos racionales en un círculo unitario
Fórmula de Euclides para un triple pitagórico
- a=m2− − n2,b=2mn,c=m2+n2{displaystyle a=m^{2}-n^{2},quad b=2mn,quad c=m^{2}+n^{2}
puede entenderse en términos de la geometría de puntos racionales en el círculo unitario (Trautman 1998).
De hecho, un punto en el plano cartesiano con coordenadas (x, y) pertenece al círculo unitario si x2 + y2 = 1. El punto es racional si x y y son números racionales, es decir, si hay enteros coprimos a, b, c tal que
- ()ac)2+()bc)2=1.{fnMicrosoft Sans Serif} {biggr}}}{2}+{biggl (}{frac}{frac}{biggr)} {biggr} {biggl}{biggl} {f}{biggl} {f}}} {fnMicroc} {b}{y}{2}=1.}
Al multiplicar ambos miembros por c2, se puede ver que los puntos racionales del círculo están en uno Correspondencia biunívoca con las ternas pitagóricas primitivas.
El círculo unitario también se puede definir mediante una ecuación paramétrica
- x=1− − t21+t2Sí.=2t1+t2.{displaystyle x={frac {1-t^{2}{1+t^{2}}quad Y... {2t}{1+t^{2}}}
Fórmula de Euclides para las ternas pitagóricas y la relación inversa t = y / (x + 1) significa que, a excepción de (−1, 0), un punto (x, y) en el círculo es racional si y solo si el valor correspondiente de t es un número racional. Tenga en cuenta que t = y / (x + 1) = b / (a + c) = n / m es también la tangente de la mitad del ángulo que está enfrente del lado del triángulo de longitud b.
Enfoque estereográfico

Existe una correspondencia entre puntos del círculo unitario con coordenadas racionales y ternas pitagóricas primitivas. En este punto, las fórmulas de Euclides se pueden derivar mediante métodos de trigonometría o, de manera equivalente, mediante el uso de la proyección estereográfica.
Para el enfoque estereográfico, suponga que P′ es un punto en la x-eje con coordenadas racionales
- P.=()mn,0).{displaystyle P'=left({frac {m} {n},0right).}
Entonces, se puede demostrar mediante álgebra básica que el punto P tiene coordenadas
- P=()2()mn)()mn)2+1,()mn)2− − 1()mn)2+1)=()2mnm2+n2,m2− − n2m2+n2).{displaystyle P=left({frac {2left({frac {}{n}right)}{left({frac {frac} {fn}fn} {fn}}} {fnfnh}}}} {fn} {fn} {fn}fn}} {fnfnfn}} {fnfn}}}} {fnm} {fnfnfnfnfnhnfnhnhnfnhnhnhnhnhnhnhnhnhnhn}}}}}}fnfnfnhn}fnh00fnhnhnhnfnfnfnhnhnfnhnhnhnhnhnhnhnhn}}}}}fnhnhnfnhnhnfnhnh00}fnfnhnhn}fnhnh}fnhnh00}fnhnh}}}fnh {m} {n}right)}{2}+1}right)=left({frac] {2mn}{m^{2}+n^{2}}} {frac {m^{2}-n^{2}} {m^{2}}derecha).}
Esto establece que cada punto racional del eje x pasa a un punto racional del círculo unitario. Lo contrario, que cada punto racional del círculo unitario proviene de tal punto del eje x, sigue aplicando la proyección estereográfica inversa. Suponga que P(x, y) es un punto del círculo unitario con x y y números racionales. Luego el punto P′ obtenido por proyección estereográfica sobre la x -el eje tiene coordenadas
- ()x1− − Sí.,0){displaystyle left({frac {x}{1-y}},0right)}
que es racional.
En términos de geometría algebraica, la variedad algebraica de puntos racionales en el círculo unitario es birracional a la línea afín sobre los números racionales. El círculo unitario se llama así una curva racional, y es este hecho el que permite una parametrización explícita de los puntos (número racional) en él por medio de funciones racionales.
Triángulos de Pitágoras en una red 2D
Una celosa 2D es un conjunto regular de puntos aislados donde si algún punto es elegido como el origen cartesiano (0, 0), entonces todos los otros puntos están en ()x, Sí.) Donde x y Sí. rango sobre todos los enteros positivos y negativos. Cualquier triángulo pitagórico con triple ()a, b, c) se puede dibujar dentro de una celosa 2D con vértices en coordenadas (0, 0), ()a, 0) y (0, b). El recuento de puntos de celo que mienten estrictamente dentro de los límites del triángulo es dado por ()a− − 1)()b− − 1)− − gcd()a,b)+12;{displaystyle {tfrac {(a-1)(b-1)-gcd {(a,b)}+1}{2}}} para los primitivos Pythagorean triples este recuento de celo interior es()a− − 1)()b− − 1)2.{displaystyle {tfrac {(a-1)}{2}} El área (por el teorema de Pick igual a uno menos que el recuento interior más la mitad del recuento de la rejilla límite) es igualab2{displaystyle {tfrac {ab}{2}}.
La primera aparición de dos ternas pitagóricas primitivas que comparten la misma área ocurre con triángulos con lados (20, 21, 29), (12, 35, 37) y área común 210 (secuencia A093536 en el OEIS). La primera aparición de dos ternas pitagóricas primitivas que comparten el mismo recuento de celosía interior ocurre con (18108, 252685, 253333), (28077, 162964, 165365) y el recuento de celosía interior 2287674594 (secuencia A225760 en el OEIS). Se han encontrado tres ternas pitagóricas primitivas compartiendo la misma área: (4485, 5852, 7373), (3059, 8580, 9109), (1380, 19019, 19069) con área 13123110. Hasta el momento, no se ha encontrado ningún conjunto de tres ternas pitagóricas primitivas que compartan el mismo número de redes interiores.
Enumeración de ternas pitagóricas primitivas
Por la fórmula de Euclides todos los primitivos trillizos pitagóricos pueden ser generados por enteros m{displaystyle m} y n{displaystyle n} con n>0}" xmlns="http://www.w3.org/1998/Math/MathML">m■n■0{displaystyle m confían confianza0}n>0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a80d02f2a5ba7e75d5878972baa2e8b4359e73c0" style="vertical-align: -0.338ex; width:10.794ex; height:2.176ex;"/>, m+n{displaystyle m+n} extraño gcd()m,n)=1{displaystyle gcd(m,n)=1}. Por lo tanto hay un mapa de 1 a 1 de los racionales (en términos más bajos) a los primitivos trillizos pitagóricos donde nm{displaystyle {tfrac {n} {fn}} {fn}} {fn}} {fn}}} {fn}}} está en el intervalo ()0,1){displaystyle (0,1)} y m+n{displaystyle m+n} extraño.
El mapeo inverso de un triple primitivo ()a,b,c){displaystyle (a,b,c)} Donde b>a>0}" xmlns="http://www.w3.org/1998/Math/MathML">c■b■a■0{displaystyle c]b confíaa confianza0}b>a>0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/67e24dccdef3826e12e7517d673eb7bb918bc049" style="vertical-align: -0.338ex; width:13.692ex; height:2.176ex;"/> a un criterio racional nm{displaystyle {tfrac {n} {fn}} {fn}} {fn}} {fn}}} {fn}}} se logra estudiando las dos sumas a+c{displaystyle a+c} y b+c{displaystyle b+c}. Una de estas sumas será un cuadrado que puede equipararse a ()m+n)2{displaystyle (m+n)} {2} y el otro será dos veces un cuadrado que se puede equiparar a 2m2{displaystyle 2m^{2}. Entonces es posible determinar el racional nm{displaystyle {tfrac {n} {fn}} {fn}} {fn}} {fn}}} {fn}}}.
Para enumerar primitivos Pythagorean triplica el racional se puede expresar como un par ordenado ()n,m){displaystyle (n,m)} y mapeado a un entero usando una función de emparejamiento como la función de emparejamiento de Cantor. Un ejemplo se puede ver en (sequence A277557 en el OEIS). Empieza
- 8,18,19,32,33,34,...... {displaystyle 8,18,19,32,33,34,} y da fundamentos
- 12,23,14,34,25,16,...... {fnMicroc {2},{tfrac {2}},{tfrac {2}} {tfrac {1}{4}}}},{tfrac {4}},{tfrac {2}{5}}},{tfrac {1}{6}}}}}}}}}}} {dots} estos, a su vez, generan triples primitivos
- ()3,4,5),()5,12,13),()8,15,17),()7,24,25),()20,21,29),()12,35,37),...... {displaystyle (3,4,5),(5,12,13),(8,15,17),(7,24,25),(20,21,29),(12,35,37),dots }
Spinors y el grupo modular
Las ternas pitagóricas también se pueden codificar en una matriz cuadrada de la forma
- X=[c+baac− − b].{displaystyle X={begin{bmatrix}c+b implicaa\a recurc-bend{bmatrix}}
Una matriz de esta forma es simétrica. Además, el determinante de X es
- DetX=c2− − a2− − b2{displaystyle det X=c^{2}-a^{2}-b^{2},}
que es cero precisamente cuando (a,b,c) es un terna pitagórica. Si X corresponde a una terna pitagórica, entonces como matriz debe tener rango 1.
Dado que X es simétrico, de un resultado en álgebra lineal se deduce que existe un vector columna ξ = [m n]T tal que el producto exterior
- X=2[mn][mn]=2.. .. T{displaystyle X=2{begin{bmatrix}mnend{bmatrix}[m n]=2xi xi ^{T},}
()1)
se mantiene, donde la T denota la transposición de la matriz. El vector ξ se llama espinor (por el grupo de Lorentz SO(1, 2)). En términos abstractos, la fórmula de Euclides significa que cada terna pitagórica primitiva puede escribirse como el producto exterior consigo mismo de un espinor con entradas enteras, como en (1).
El grupo modular Γ es el conjunto de matrices 2×2 con entradas enteras
- A=[α α β β γ γ δ δ ]{displaystyle A={begin{bmatrix}alpha &beta \gamma &delta end{bmatrix}}
con determinante igual a uno: αδ − βγ = 1. Este conjunto forma un grupo, ya que la inversa de una matriz en Γ está de nuevo en Γ, al igual que el producto de dos matrices en Γ. El grupo modular actúa sobre la colección de todos los espinores enteros. Además, el grupo es transitivo en la colección de espinores enteros con entradas relativamente primos. Porque si [m n]T tiene entradas relativamente principales, entonces
- [m− − vnu][10]=[mn]{begin {begin{bmatrix}m ventaja-v\nunci} {begin{bmatrix} {begin{bmatrix}1end{bmatrix}={begin{bmatrix}mnenend{bmatrix}}}}}}}}}}}}}}}
donde se seleccionan u y v (por el algoritmo euclidiano) de modo que mu + nv = 1.
Al actuar sobre el espinor ξ en (1), la acción de Γ pasa a una acción sobre las ternas pitagóricas, siempre que se permitan ternas con posibles componentes negativas. Por lo tanto, si A es una matriz en Γ, entonces
- 2()A.. )()A.. )T=AXAT{displaystyle 2(Axi)(Axi)}=AXA^{T},}
()2)
da lugar a una acción sobre la matriz X en (1). Esto no da una acción bien definida sobre los triples primitivos, ya que puede llevar un triple primitivo a uno imprimitivo. Es conveniente en este punto (según Trautman 1998) llamar a un triple (a,b,c) estándar si c > 0 y (a,b,c) son primos relativos o (a/2,b/2,c/2) son relativamente primos con a/2 impar. Si el espinor [m n]T tiene entradas relativamente primos, entonces el triple asociado (a,b,c) determinado por (1) es un triple estándar. De ello se deduce que la acción del grupo modular es transitiva sobre el conjunto de triples estándar.
Como alternativa, restrinja la atención a los valores de m y n para el cual m es impar y n es par. Sea el subgrupo Γ(2) de Γ el núcleo del homomorfismo de grupos
- .. =SL()2,Z)→ → SL()2,Z2){displaystyle Gamma =mathrm {SL} (2,mathbf {Z})to mathrm {SL} (2,mathbf {Z} _{2}}}
donde SL(2,Z2) es el grupo lineal especial sobre el campo finito Z2 de enteros módulo 2. Entonces Γ(2) es el grupo de transformaciones unimodulares que preservan la paridad de cada entrada. Por lo tanto, si la primera entrada de ξ es impar y la segunda entrada es par, entonces lo mismo se aplica a Aξ para todos los A ∈ Γ(2). De hecho, bajo la acción (2), el grupo Γ(2) actúa transitivamente sobre el conjunto de ternas pitagóricas primitivas (Alperin 2005).
El grupo Γ(2) es el grupo libre cuyos generadores son las matrices
- U=[1201],L=[1021].{displaystyle U={begin{bmatrix}1 tendría2 diez1end{bmatrix}qquad L={begin{bmatrix}1 ventaja02 limitada1end{bmatrix}}
En consecuencia, cada terna pitagórica primitiva se puede obtener de forma única como producto de copias de las matrices U y L.
Relaciones padre/hijo
Por un resultado de Berggren (1934), todas las ternas pitagóricas primitivas pueden generarse a partir del triángulo (3, 4, 5) usando las tres transformaciones lineales T1, T2 , T3 a continuación, donde a, b , c son lados de un triple:
| nuevo lado a | nuevo lado b | nuevo lado c | |
| T1: | a − 2b + 2c | 2a − b + 2c | 2a − 2b + 3c |
| T2: | a + 2b + 2c | 2a + b + 2c | 2a + 2b + 3c |
| T3: | −a + 2b + 2c | −2a + b + 2c | −2a + 2b + 3c |
En otras palabras, cada triple primitivo será un "padre" a tres triples primitivos adicionales. Comenzando desde el nodo inicial con a = 3, b = 4, y c = 5, la operación T1 produce el nuevo triple
- (3 − (2×4) + (2×5), (2×3) − 4 + (2×5), (2×3) − (2×4) + (3×5)) = (5, 12, 13),
y de manera similar T2 y T3 producen el triples (21, 20, 29) y (15, 8, 17).
Las transformaciones lineales T1, T2 y T3 tienen una interpretación geométrica en el lenguaje de las formas cuadráticas. Están estrechamente relacionados (pero no son iguales) a los reflejos que generan el grupo ortogonal de x2 + y2 − z2 sobre los enteros.
Relación con enteros gaussianos
Alternativamente, las fórmulas de Euclides se pueden analizar y probar usando los enteros gaussianos. Los enteros gaussianos son números complejos de la forma α = u + vi, donde u y v son números enteros ordinarios y i es la raíz cuadrada de uno negativo. Las unidades de los enteros gaussianos son ±1 y ±i. Los enteros ordinarios se denominan enteros racionales y se denotan como 'Z'. Los enteros gaussianos se indican como Z[i]. El lado derecho del teorema de Pitágoras se puede factorizar en enteros gaussianos:
- c2=a2+b2=()a+bi)()a+bi)̄ ̄ =()a+bi)()a− − bi).{displaystyle c^{2}=a^{2}+b^{2}=(a+bi){overline {(a+bi)}=(a+bi)(a-bi). }
Una terna pitagórica primitiva es aquella en la que a y b son coprimos, es decir, no comparten factores primos en los números enteros. Para tal triple, ya sea a o b es par, y el otro es impar; de esto, se deduce que c también es impar.
Los dos factores z:= a + bi y z*:= a − bi de un triple pitagórico primitivo, cada uno igual al cuadrado de un entero gaussiano. Esto se puede demostrar utilizando la propiedad de que cada entero gaussiano se puede factorizar de forma única en números primos gaussianos hasta las unidades. (Esta factorización única se deriva del hecho de que, en términos generales, se puede definir una versión del algoritmo euclidiano sobre ellos). La demostración consta de tres pasos. Primero, si a y b no comparten factores primos en el enteros, entonces tampoco comparten factores primos en los enteros gaussianos. (Suponga que a = gu y b = gv con enteros gaussianos g, u y v y g no son una unidad Entonces u y v se encuentran en la misma línea a través de la origen. Todos los enteros gaussianos en dicha línea son múltiplos enteros de algún entero gaussiano h. Pero entonces el entero gh ≠ ±1 divide tanto a como b). En segundo lugar, se deduce que z y z* tampoco comparten factores primos en los enteros gaussianos. Porque si lo hicieran, entonces su divisor común δ también dividiría z + z* = 2a y z − z* = 2ib. Dado que a y b son coprimos, eso implica que δ divide 2 = (1 + i)(1 − i) = i(1 − i)2 . De la fórmula c2 = zz*, eso a su vez implicaría que c es par, contrariamente a la hipótesis de una terna pitagórica primitiva. En tercer lugar, dado que c2 es un cuadrado, cada primo gaussiano en su factorización se duplica, es decir, parece un número par de tiempos Dado que z y z* no comparten factores primos, esta duplicación también es cierto para ellos. Por lo tanto, z y z* son cuadrados.
Por lo tanto, el primer factor se puede escribir
- a+bi=ε ε ()m+ni)2,ε ε ▪ ▪ {}± ± 1,± ± i}.{displaystyle a+bi=varepsilon left(m+niright)^{2},quad varepsilon in {pm 1,pm i}
Las partes real e imaginaria de esta ecuación dan las dos fórmulas:
- {}ε ε =+1,a=+()m2− − n2),b=+2mn;ε ε =− − 1,a=− − ()m2− − n2),b=− − 2mn;ε ε =+i,a=− − 2mn,b=+()m2− − n2);ε ε =− − i,a=+2mn,b=− − ()m2− − n2).{displaystyle {begin{cases}varepsilon =+1, limitquad a=+left(m^{2}-n^{2}right),quad b=+2mn;\varepsilon =-1, limitadaquad a=-left(m^{2}-n^{2}right),quad b=-2mn;\varepsilon =+i, pacientequad a=-2mn,quad b=+left(m^{2}-n^{2}right);\varepsilon =-i, limitquad a=+2mn,quad b=-left(m^{2}-n^{2}right)end{cases}}
Para cualquier terna pitagórica primitiva, debe haber números enteros m y n tales que estas dos ecuaciones se satisfacen. Por lo tanto, cada terna pitagórica puede generarse a partir de alguna elección de estos enteros.
Como enteros gaussianos cuadrados perfectos
Si consideramos el cuadrado de un entero gaussiano, obtenemos la siguiente interpretación directa de la fórmula de Euclides como representación del cuadrado perfecto de un entero gaussiano.
- ()m+ni)2=()m2− − n2)+2mni.{displaystyle (m+ni)}=(m^{2}-n^{2})+2mni.}
Usando los hechos que los enteros gausianos son un dominio euclidiano y que para un integer gaisiano p SilenciopSilencio2{displaystyle Новывый } es siempre un cuadrado es posible mostrar que un triple pitagórico corresponde a la plaza de un primer entero gausiano si la hipotenusa es primordial.
Si el entero Gaussiano no es primo entonces es el producto de dos enteros gausianos p y q con SilenciopSilencio2{displaystyle Новывый } y SilencioqSilencio2{displaystyle Silencioq habit^{2} enteros. Puesto que las magnitudes se multiplican en los enteros gausianos, el producto debe ser SilenciopSilencioSilencioqSilencio{displaystyle TENIDO RESPUESTA, que cuando cuadrado para encontrar un triple pitagórico debe ser compuesto. El contrapositivo completa la prueba.
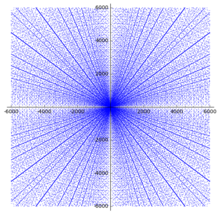
Distribución de triples
Hay una serie de resultados sobre la distribución de las ternas pitagóricas. En el diagrama de dispersión, ya son evidentes una serie de patrones obvios. Cada vez que los catetos (a,b) de un triple primitivo aparecen en el gráfico, todos los múltiplos enteros de (a,b) también debe aparecer en el diagrama, y esta propiedad produce la apariencia de líneas que irradian desde el origen en el diagrama.
Dentro de la dispersión, hay conjuntos de patrones parabólicos con una alta densidad de puntos y todos sus focos en el origen, abriéndose en las cuatro direcciones. Diferentes parábolas se cruzan en los ejes y parecen reflejarse fuera del eje con un ángulo de incidencia de 45 grados, con una tercera parábola entrando de forma perpendicular. Dentro de este cuadrante, cada arco centrado en el origen muestra la sección de la parábola que se encuentra entre su punta y su intersección con su semilato recto.
Estos patrones pueden explicarse como sigue. Si a2/4n{displaystyle a^{2}/4n} es un entero, entonces (a, Silencion− − a2/4nSilencio{displaystyle Silencio., n+a2/4n{displaystyle n+a^{2}/4n}Es un triple pitagórico. (De hecho cada triple pitagórico) ()a, b, c) puede ser escrito de esta manera con entero n, posiblemente después de intercambiar a y b, desde n=()b+c)/2{displaystyle n=(b+c)/2} y a y b ambos no pueden ser extraños.) Los triples pitagóricos se encuentran así en curvas dadas por b=Silencion− − a2/4nSilencio{displaystyle b= habitn-a^{2}/, es decir, parabolas reflejadas en a-eje, y las curvas correspondientes con a y b intercambiado. Si a es variado para un dado n (es decir, en una parabola dada), valores enteros b ocurre con frecuencia si n es un cuadrado o un pequeño múltiplo de un cuadrado. Si varios de estos valores se encuentran unidos, los parabolas correspondientes coinciden aproximadamente, y los triples se agrupan en una estrecha tira parabólica. Por ejemplo, 382 = 1444, 2 × 272 = 1458, 3 × 222 = 1452, 5 × 172 = 1445 y 10 × 122 = 1440; la correspondiente tira parabólica alrededor n ■ 1450 es claramente visible en la parcela de dispersión.
Las propiedades angulares descritas anteriormente se derivan inmediatamente de la forma funcional de las parábolas. Las parábolas se reflejan en el eje a en a = 2 n, y la derivada de b con respecto a a en este punto es –1; por tanto, el ángulo de incidencia es de 45°. Dado que los conglomerados, como todos los triples, se repiten en múltiplos enteros, el valor 2n también corresponde a un conglomerado. La parábola correspondiente se cruza con el eje b en ángulo recto en b = 2n, y por lo tanto su reflejo en el intercambio de a y b corta el eje a en ángulo recto en a = 2n, precisamente donde la parábola para n se refleja en el un-eje. (Por supuesto, lo mismo es cierto para a y b intercambiados.)
Albert Fässler y otros brindan información sobre la importancia de estas parábolas en el contexto de los mapeos conformes.
Casos especiales y ecuaciones relacionadas
La secuencia platónica
El caso n = 1 de la construcción más general de las ternas pitagóricas se conoce desde hace mucho tiempo. Proclo, en su comentario a la Proposición 47 del primer libro de los Elementos de Euclides, lo describe de la siguiente manera:
Ciertos métodos para el descubrimiento de triángulos de este tipo se entregan, uno que se refieren a Platón, y otro a Pitágoras. (Este último) comienza de números impares. Porque hace que el número impar más pequeño de los lados sobre el ángulo recto; luego toma el cuadrado de él, resta unidad y hace la mitad de la diferencia mayor de los lados sobre el ángulo recto; por último añade unidad a esto y así forma el lado restante, el hipotenusa.
... Para el método de Platón argumenta incluso de números. Toma el número dado y lo hace uno de los lados sobre el ángulo recto; luego, bisectando este número y equilibrando la mitad, añade unidad a la plaza para formar la hipotenusa, y resta unidad desde la plaza para formar el otro lado sobre el ángulo recto.... Así ha formado el mismo triángulo que fue obtenido por el otro método.
En forma de ecuación, esto se convierte en:
a es impar (Pitágoras, c. 540 a. C.):
- ladoa:ladob=a2− − 12:ladoc=a2+12.{displaystyle {text{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f}fnMicrosoft{f}fnMicrosoft {fnMicrosoft {f}f}fnMicro {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f}\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\\f}f}fnMicro {fnMicro {\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMi }a:{text{side {}b={a^{2}-1 over 2}:{text{side }c={a^{2}+1 over 2}
a es par (Platón, c. 380 a. C.):
- ladoa:ladob=()a2)2− − 1:ladoc=()a2)2+1{displaystyle {text{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f {fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {f}fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\f}fnMicrosoft {fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f}f}fnMicro {fnMicrosoft {f}fnMicrosoft {fnMicro {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicro {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicro }a:{text{side }b=left({a over 2}right)^{2}-1:{text{side }c=left({a over 2}right)^{2}+1}
Se puede demostrar que todas las ternas pitagóricas se pueden obtener, con el cambio de escala apropiado, a partir de la secuencia platónica básica (a, (a2 − 1)/2 y (a2 + 1)/2) al permitir que a tome valores racionales no enteros. Si a se reemplaza con la fracción m/n en la secuencia, el resultado es igual al 'estándar' generador triple (2mn, m2 − n2 ,m2 + n2 ) después de cambiar la escala. De ello se deduce que cada triple tiene un valor a racional correspondiente que se puede usar para generar un triángulo similar (uno con los mismos tres ángulos y con lados en las mismas proporciones que el original). Por ejemplo, el equivalente platónico de (56, 33, 65) es generado por a = m /n = 7/4 como (a, (a2 –1)/2, (a2+1)/2) = (56/32, 33/32, 65/32) . La secuencia platónica en sí se puede derivar siguiendo los pasos para 'dividir el cuadrado' descrito en Diofanto II.VIII.
La ecuación de Jacobi-Madden
La ecuación,
- a4+b4+c4+d4=()a+b+c+d)4{displaystyle a^{4}+b^{4}+c^{4}+d^{4}=(a+b+c+d)^{4}
es equivalente a la terna pitagórica especial,
- ()a2+ab+b2)2+()c2+cd+d2)2=()()a+b)2+()a+b)()c+d)+()c+d)2)2{displaystyle (a^{2}+ab+b^{2})^{2}+(c^{2}+cd+d^{2})^{2}=(a+b)^{2}+(a+b)(c+d)+(c+d)^{2})^{2}}}}
Hay un número infinito de soluciones para esta ecuación, ya que resolver las variables implica una curva elíptica. Los pequeños son,
- a,b,c,d=− − 2634,955,1770,5400{displaystyle a,b,c,d=-2634,955,1770,5400}
- a,b,c,d=− − 31764,7590,27385,48150{displaystyle a,b,c,d=-31764,7590,27385,48150}
Sumas iguales de dos cuadrados
Una manera de generar soluciones a2+b2=c2+d2{displaystyle a^{2}+b^{2}=c^{2}+d^{2} es parametrizar a, b, c, d en términos de enteros m, n, p, q como sigue:
- ()m2+n2)()p2+q2)=()mp− − nq)2+()np+mq)2=()mp+nq)2+()np− − mq)2.{displaystyle (m^{2}+n^{2})(p^{2}+q^{2})=(mp-nq)^{2}+(np+mq)^{2}=(mp+nq)^{2}+(np-mq)^{2}}}
Sumas iguales de dos cuartas potencias
Dados dos conjuntos de ternas pitagóricas,
- ()a2− − b2)2+()2ab)2=()a2+b2)2{displaystyle (a^{2}-b^{2})^{2}+(2ab)^{2}=(a^{2}+b^{2})}}
- ()c2− − d2)2+()2cd)2=()c2+d2)2{displaystyle (c^{2}-d^{2})^{2}+(2cd)^{2}=(c^{2}+d^{2}}}}
el problema de encontrar productos iguales de un lado sin hipotenusa y la hipotenusa,
- ()a2− − b2)()a2+b2)=()c2− − d2)()c2+d2){displaystyle (a^{2}-b^{2})(a^{2}+b^{2})=(c^{2}-d^{2})(c^{2}+d^{2})}
se ve fácilmente como equivalente a la ecuación,
- a4− − b4=c4− − d4{displaystyle a^{4}-b^{4}=c^{4}-d^{4}
y fue resuelto por Euler como a,b,c,d=133,59,158,134{displaystyle a,b,c,d=133,59,158,134}. Puesto que mostró esto es un punto racional en una curva elíptica, entonces hay un número infinito de soluciones. De hecho, también encontró una parametrización polinomio de 7o grado.
Descartes' Teorema del círculo
Para el caso de Descartes' teorema del círculo donde todas las variables son cuadrados,
- 2()a4+b4+c4+d4)=()a2+b2+c2+d2)2{displaystyle 2(a^{4}+b^{4}+c^{4}+d^{4})=(a^{2}+b^{2}+c^{2}+d^{2}}
Euler demostró que esto es equivalente a tres ternas pitagóricas simultáneas,
- ()2ab)2+()2cd)2=()a2+b2− − c2− − d2)2{displaystyle (2ab)^{2}+(2cd)^{2}=(a^{2}+b^{2}-c^{2}-d^{2})}
- ()2ac)2+()2bd)2=()a2− − b2+c2− − d2)2{displaystyle (2ac)^{2}+(2bd)^{2}=(a^{2}-b^{2}+c^{2}-d^{2})}}
- ()2ad)2+()2bc)2=()a2− − b2− − c2+d2)2{displaystyle (2ad)^{2}+(2bc)}=(a^{2}-b^{2}-c^{2}+d^{2}}} {2}}}}
También hay un número infinito de soluciones, y para el caso especial cuando a+b=c{displaystyle a+b=c}, entonces la ecuación simplifica,
- 4()a2+ab+b2)=d2{displaystyle 4(a^{2}+ab+b^{2}=d^{2}
con pequeñas soluciones a,b,c,d=3,5,8,14{displaystyle a,b,c,d=3,5,8,14} y puede ser resuelto como formas cuadráticas binarias.
Triples pitagóricos casi isósceles
Ninguna terna pitagórica es isósceles, porque la relación entre la hipotenusa y el otro lado es √2 , pero √2 no se puede expresar como la razón de 2 enteros.
Hay, sin embargo, triángulos rectángulos con lados enteros para los cuales las longitudes de los lados que no son hipotenusa difieren en uno, como por ejemplo,
- 32+42=52{displaystyle 3^{2}+4^{2}=5^{2}
- 202+212=292{displaystyle 20^{2}+21^{2}=29^{2}
y un número infinito de otros. Se pueden parametrizar completamente como,
- ()x− − 12)2+()x+12)2=Sí.2{displaystyle left({tfrac {x-1}{2}right)}{2}+left({tfrac {x+1}{2}}right)^{2}=y^{2}}}
Dondex, y} son las soluciones a la ecuación Pell x2− − 2Sí.2=− − 1{displaystyle x^{2}-2y^{2}=-1}.
Si a, b, c son los lados de este tipo de terna pitagórica primitiva (PPT), entonces la solución a la ecuación de Pell viene dada por la fórmula recursiva
- an=6an− − 1− − an− − 2+2{displaystyle a_{n}=6a_{n-1}-a_{n-2}+2} con a1=3{displaystyle A_{1}=3} y a2=20{displaystyle A_{2}=20}
- bn=6bn− − 1− − bn− − 2− − 2{displaystyle b_{n}=6b_{n-1}-b_{n-2}-2} con b1=4{displaystyle B_{1}=4} y b2=21{displaystyle B_{2}=21}
- cn=6cn− − 1− − cn− − 2{displaystyle C_{n}=6c_{n-1}-c_{n-2} con c1=5{displaystyle C_{1}=5} y c2=29{displaystyle C_{2}=29}.
Esta secuencia de PPT forma el tallo central (tronco) del árbol ternario enraizado de PPT.
Cuando son el lado más largo sin hipotenusa y la hipotenusa los que difieren en uno, como en
- 52+122=132{displaystyle 5^{2}+12^{2}=13^{2}}
- 72+242=252{displaystyle 7^{2}+24^{2}=25^{2}
entonces la solución completa para el PPT a, b, c es
- a=2m+1,b=2m2+2m,c=2m2+2m+1{displaystyle a=2m+1,quad b=2m^{2}+2m,quad c=2m^{2}+2m+1}
y
- ()2m+1)2+()2m2+2m)2=()2m2+2m+1)2{displaystyle (2m+1)^{2}+(2m^{2}+2m)}=(2m^{2m}+2m+1)}{2}}}
donde el entero 0}" xmlns="http://www.w3.org/1998/Math/MathML">m■0{displaystyle m confía0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/501173910e6da8425b4e9d44a4e8643620bc2464" style="vertical-align: -0.338ex; width:6.301ex; height:2.176ex;"/> es el parámetro generador.
Muestra que todos los números impares (mayores que 1) aparecen en este tipo de PPT casi isósceles. Esta secuencia de PPT forma el tallo exterior del lado derecho del árbol ternario enraizado de PPT.
Otra propiedad de este tipo de PPT casi isósceles es que los lados están relacionados de tal manera que
- ab+ba=Kc{displaystyle a^{b}+b^{a}=Kc}
para algunos enteros K{displaystyle K}. O en otras palabras ab+ba{displaystyle a^{b}+b^{a} es divisible por c{displaystyle c} tales como
- ()512+125)/13=18799189{displaystyle (5^{12}+12^{5})/13=18799189}.
Números de Fibonacci en ternas pitagóricas
A partir del 5, cada segundo número de Fibonacci es la longitud de la hipotenusa de un triángulo rectángulo de lados enteros, es decir, el mayor número de una terna pitagórica, obtenido de la fórmula
- (3,4,5), (5,12,13), (16,30,34), (39,80,89),...
El lado central de cada uno de estos triángulos es la suma de los tres lados del triángulo anterior.
Generalizaciones
Hay varias formas de generalizar el concepto de ternas pitagóricas.
N-tupla pitagórica
La expresión
- ()m12− − m22− − ...... − − mn2)2+.. k=2n()2m1mk)2=()m12+...... +mn2)2{displaystyle left(m_{1}{2}-m_{2}{2}-ldots -m_{n}^{2}right)^{2}+sum ¿Por qué? ¿Qué?
es una n-tupla pitagórica para cualquier tupla de enteros positivos ( m1,..., mn) con m2
1 > m2
2 +... + m2
n. La n-tupla de Pitágoras se puede volver primitiva dividiendo por el máximo común divisor de sus valores.
Además, cualquier pitagórico primitivo n-tupla a 2
1 +... + a2
n = c2 se puede encontrar con este enfoque. Utilice (m1,..., mn ) = (c + a1, a2,..., an) para obtener un pitagórico n-tuple por la fórmula anterior y se divide por el divisor entero común más grande, que es 2m1 = 2(c + a1). Dividiendo por el máximo común divisor de estos (m1,..., m n) valores da el mismo primitivo pitagórico n-tuple; y hay una correspondencia biunívoca entre tuplas de enteros positivos coprimos entre conjuntos (m1,..., mn) satisfaciendo m2
1 > m2
2 +... + m2
n y n-tuplas primitivas pitagóricas.
Ejemplos de la relación entre los valores de coprime ajustados m→ → {displaystyle {vec}} Pythagorean primitivo n-tuples include:
- m→ → =()1)Administración Administración 12=12m→ → =()2,1)Administración Administración 32+42=52m→ → =()2,1,1)Administración Administración 12+22+22=32m→ → =()3,1,1,1)Administración Administración 12+12+12+12=22m→ → =()5,1,1,2,3)Administración Administración 12+12+12+22+32=42m→ → =()4,1,1,1,1,2)Administración Administración 12+12+12+12+12+22=32m→ → =()5,1,1,1,2,2,2)Administración Administración 12+12+12+12+22+22+22=42{displaystyle {begin{aligned}{vec} {2}\c}==(2,1) âTMaleftrightarrow 3^{2}+4^{2}=5^{2} {2}\\\vec}=0}=0}=0}=0}=0} {2}=0}=0} {2}}=0}=0} {2}=0} {0}=0}}}} {0}=0}=0}=0}=0}}}}}=0}=0}=0}=0}=0} {0}}}=0} {0}=0}}}}}=0}}}}}}}}}}}}}}}}}}}}}}}}}}} {0} 1^{2}+1^{2}+1^{2}+1^{2}=2^{2}\{vec {m}=(5,1,2,3) 1^{2}+1^{2}+1^{2}+2^{2}+3^{2}=4^{2}\{vec {m}=(4,1,1,1,2) 1^{2}+1^{2}+1^{2}+1^{2}+1^{2}+2^{2}=3^{2}\{2}\\{m}=5,1,1,2,2)}Ponteleftrightarrow 1^{2}+1^{2}+1^{2}+2}+2^{2}+2^{2}+2^{2}=4^{2}end{aligned}
Cuadrados consecutivos
Dado que la suma F(k,m) de k cuadrados consecutivos que comienzan con m2 por la fórmula,
- F()k,m)=km()k− − 1+m)+k()k− − 1)()2k− − 1)6{displaystyle F(k,m)=km(k-1+m)+{frac {k(k-1)(2k-1)}{6}}}
uno puede encontrar valores (k, m) de modo que F(k,m) es un cuadrado, como uno de Hirschhorn donde el número de términos es en sí mismo un cuadrado,
- m=v4− − 24v2− − 2548,k=v2,F()m,k)=v5+47v48{displaystyle m={tfrac {4}-24v^{2}-25}{48};k=v^{2},;F(m,k)={tfrac {V^{5}+47v}{48}}}
y v ≥ 5 es cualquier número entero no divisible por 2 o 3. Para el caso más pequeño v = 5, por lo tanto k = 25, esto produce el conocido problema de apilamiento de balas de cañón de Lucas,
- 02+12+22+⋯ ⋯ +242=702{displaystyle 0^{2}+1^{2}+2^{2}+dots +24^{2}=70^{2}
un hecho que está conectado a la red Leech.
Además, si en una n-tupla pitagórica (n ≥ 4) todos los sumandos son consecutivos excepto uno, uno puede usar la ecuación,
- F()k,m)+p2=()p+1)2{displaystyle F(k,m)+p^{2}=(p+1)^{2}
Desde el segundo poder p cancela, esto es sólo lineal y fácil de resolver para p=F()k,m)− − 12{displaystyle p={tfrac {F(k,m)-1}{2}} Aunque k, m debe ser elegido para p es un entero, con un pequeño ejemplo siendo k = 5, m = 1 ceder,
- 12+22+32+42+52+272=282{displaystyle 1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+27^{2}=28^{2}}
Por lo tanto, una forma de generar n-tuplas pitagóricas es usando, para varias x ,
- x2+()x+1)2+⋯ ⋯ +()x+q)2+p2=()p+1)2,{displaystyle x^{2}+(x+1)^{2}+cdots +(x+q)^{2}+p^{2}=(p+1)^{2}}
donde q = n–2 y donde
- p=()q+1)x2+q()q+1)x+q()q+1)()2q+1)6− − 12.{displaystyle p={frac {(q+1)x^{2}+q(q+1)x+{frac {q(q+1)(2q+1)}{6}}{2}}}} {} {}} {f}} {f}
El último teorema de Fermat
Una generalización del concepto de ternas pitagóricas es la búsqueda de ternas de enteros positivos a, b, y c, tal que an + bn = cn, para algún n estrictamente mayor que 2. Pierre de Fermat en 1637 afirmó que no existe tal triple, una afirmación que se conoció como el último teorema de Fermat porque tomó más tiempo que cualquier otra conjetura de Fermat para ser probada o refutada. La primera prueba la dio Andrew Wiles en 1994.
N − 1 o n potencias n sumando una potencia n
Otra generalización es buscar secuencias de n + 1 enteros positivos para los que nésima potencia del último es la suma de las nésima potencias de los términos anteriores. Las secuencias más pequeñas para valores conocidos de n son:
- n = 3: {3, 4, 5; 6}.
- n = 4: {30, 120, 272, 315; 353}
- n = 5: {19, 43, 46, 47, 67; 72}
- n = 7: {127, 258, 266, 413, 430, 439, 525; 568}
- n = 8: {90, 223, 478, 524, 748, 1088, 1190, 1324; 1409}
Para el n = 3 caso, en el que x3+Sí.3+z3=w3,{displaystyle x^{3}+y^{3}+z^{3}=w^{3} llamado Fermat cubic, una fórmula general existe dando todas las soluciones.
Una generalización ligeramente diferente permite la suma de (k + 1) nésimas potencias para igualar la suma de (n − k) nésimas potencias. Por ejemplo:
- ()n = 3): 13 + 123 = 93 + 103, hecho famoso por el recuerdo de Hardy de una conversación con Ramanujan sobre el número 1729 siendo el número más pequeño que se puede expresar como una suma de dos cubos de dos maneras distintas.
También pueden existir n − 1 enteros positivos cuyo nth power suma a un nth power (aunque, según el último teorema de Fermat, no para n = 3); estos son contraejemplos de la conjetura de la suma de potencias de Euler. Los contraejemplos más pequeños conocidos son
- n = 4: (95800, 217519, 414560; 422481)
- n = 5: (27, 84, 110, 133; 144)
Triángulo heroniano triple
Un triángulo heroniano se define comúnmente como uno con lados enteros cuya área también es un número entero. Las longitudes de los lados de dicho triángulo forman un triple heroniano (a, b, c) para a ≤ b ≤ c. Todo triple pitagórico es un triple heroniano, porque al menos uno de los catetos a, b debe ser par en una terna pitagórica, por lo que el área ab/2 es un número entero. Sin embargo, no todas las ternas heronianas son ternas pitagóricas, como muestra el ejemplo (4, 13, 15) con el área 24.
Si (a, b, c) es una terna heroniana, entonces es (ka, kb, kc) donde k es cualquier entero positivo; su área será el entero que es k2 veces el área entera del (a, b, c) triángulo. El triple heroniano (a, b, c) es primitivo siempre que a, b, c sean coprimos en conjunto. (Con las ternas pitagóricas primitivas también se aplica la declaración más fuerte de que son coprimos por pares, pero con los triángulos heronianos primitivos la declaración más fuerte no siempre se cumple, como con (7, 15, 20)). Aquí están algunas de las ternas heronianas primitivas más simples que no son ternas pitagóricas:
- (4, 13, 15) con área 24
- (3, 25, 26) con área 36
- (7, 15, 20) con área 42
- (6, 25, 29) con área 60
- (11, 13, 20) con área 66
- (13, 14, 15) con área 84
- (13, 20, 21) con área 126
Por la fórmula de Heron, la condición extra para un triple de enteros positivos (a, b, c) con a < b < c ser heroniano es eso
- ()a2 + b2 + c2)2 − 2a4 + b4 + c4)
o equivalente
- 2(a2b2 + a2c2 + b2c2−a4 + b4 + c4)
sea un cuadrado perfecto distinto de cero divisible por 16.
Aplicación a la criptografía
Los triples pitagóricos primitivos se han utilizado en criptografía como secuencias aleatorias y para la generación de claves.
Contenido relacionado
Función zeta de Riemann
Axiomas de Peano
Elipsoide
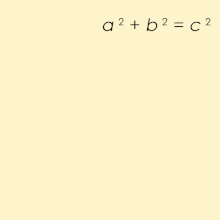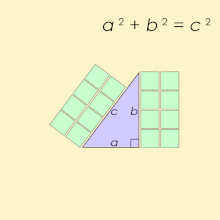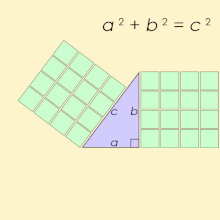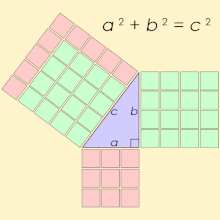
































































![X=2{begin{bmatrix}m\nend{bmatrix}}[m n]=2xi xi ^{T},](https://wikimedia.org/api/rest_v1/media/math/render/svg/248a4dd30e8590ddf33a9f53d452656dff6711ec)