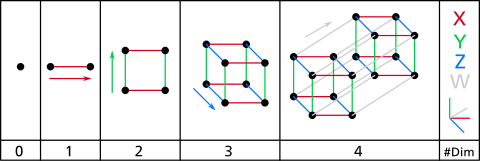Teseracto

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Analógico de cuatro dimensiones del cubo

La cruz Dalí, una red de un tesseract

El tesseract se puede desarrollar en ocho cubos en el espacio 3D, así como el cubo se puede desplegar en seis plazas en el espacio 2D.

En geometría, un tesseract es el análogo tetradimensional del cubo; el teseracto es al cubo lo que el cubo es al cuadrado. Así como la superficie del cubo consta de seis caras cuadradas, la hipersuperficie del tesseract consta de ocho celdas cúbicas. El teseracto es uno de los seis 4 politopos regulares convexos.

El tesseract también se llama 8 celdas, C₈, (regular) octachoron, octadoides, prisma cúbica, y tetracube. Es el cuatridimensional hipercube, o 4-cube como miembro de la familia dimensional de hipercubos o politopes de medida. Coxeter lo etiqueta ${displaystyle gamma _{4}}$ politopo. El término hipercube sin una referencia de dimensión se trata frecuentemente como sinónimo de este politopo específico.

El Oxford English Dictionary rastrea la palabra tesseract hasta el libro de Charles Howard Hinton de 1888 A New Era of Thought. El término deriva del griego téssara ( τέσσαρα 'cuatro') y de aktís (ἀκτίς 'ray'), refiriéndose a los cuatro bordes de cada vértice a otros vértices. Hinton originalmente deletreó la palabra como tessaract.

Geometría

Como un politopo regular con tres cubos plegados alrededor de cada borde, tiene el símbolo de Schläfli {4,3,3} con simetría hiperoctaédrica de orden 384. Construido como un hiperprisma 4D hecho de dos cubos paralelos, se puede nombrar como un símbolo de Schläfli compuesto {4,3} × { }, con un orden de simetría de 96. Como un duoprisma 4-4, un producto cartesiano de dos cuadrados, puede nombrarse mediante un símbolo de Schläfli compuesto {4}×{4}, con orden de simetría 64. Como ortotopo, se puede representar mediante el símbolo de Schläfli compuesto { } × { } × { } × { } o { }⁴, con orden de simetría 16.

Dado que cada vértice de un teseracto es adyacente a cuatro aristas, la figura del vértice del teseracto es un tetraedro regular. El politopo dual del teseracto es el de 16 celdas con el símbolo de Schläfli {3,3,4}, con el que se puede combinar para formar el compuesto de teseracto y 16 celdas.

Cada borde de un teseracto regular tiene la misma longitud. Esto es interesante cuando se usan teseractos como base para una topología de red para vincular múltiples procesadores en computación paralela: la distancia entre dos nodos es como máximo 4 y hay muchas rutas diferentes para permitir el equilibrio de peso.

Coordenadas

El tesseract estándar en el espacio euclidiano de 4 se da como el casco convexo de los puntos (±1, ±1, ±1, ±1). Es decir, consta de los puntos:

{(x_{1},x_{2},x_{3},x_{4})in mathbb {R} ^{4},:,-1leq x_{i}leq 1}

En este marco de referencia cartesiano, el teseracto tiene un radio de 2 y está delimitado por ocho hiperplanos (x_i = ±1). Cada par de hiperplanos no paralelos se cruzan para formar 24 caras cuadradas en un teseracto. Tres cubos y tres cuadrados se intersecan en cada borde. Hay cuatro cubos, seis cuadrados y cuatro aristas que se unen en cada vértice. En total, consta de 8 cubos, 24 cuadrados, 32 aristas y 16 vértices.

Neto

El despliegue de un politopo se denomina red. Hay 261 redes distintas del teseracto. Los despliegues del tesseract se pueden contar asignando las redes a árboles emparejados (un árbol junto con una combinación perfecta en su complemento).

Construcción

Una animación del cambio de dimensiones

La construcción de hipercubos se puede imaginar de la siguiente manera:

1-dimensional: Dos puntos A y B se pueden conectar para convertirse en una línea, dando un nuevo segmento de línea AB.
2-dimensional: Dos segmentos paralelos AB y CD separados por una distancia de AB se pueden conectar para convertirse en un cuadrado, con los rincones marcados como ABCD.
3-dimensional: Dos cuadrados paralelos ABCD y EFGH separados por una distancia de AB se pueden conectar para convertirse en un cubo, con las esquinas marcadas como ABCDEFGH.
4-dimensional: Dos cubos paralelos ABCDEFGH e IJKLMNOP separados por una distancia de AB se pueden conectar para convertirse en un tesseract, con los rincones marcados como ABCDEFGHIJKLMNOP. Sin embargo, este posicionamiento paralelo de dos cubos tales que sus 8 pares correspondientes de vértices están separados por una distancia de AB sólo se puede lograr en un espacio de 4 o más dimensiones.

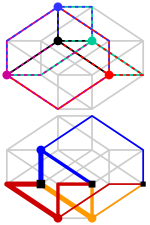
Las 8 celdas del teseracto pueden considerarse (de tres maneras diferentes) como dos anillos entrelazados de cuatro cubos.

El teseracto se puede descomponer en 4 politopos más pequeños. Es el casco convexo del compuesto de dos semiseractos (16 celdas). También se puede triangular en simples de 4 dimensiones (5 celdas irregulares) que comparten sus vértices con el teseracto. Se sabe que hay 92487256 de tales triangulaciones y que la menor cantidad de simples de 4 dimensiones en cualquiera de ellas es 16.

La disección de la tesseracta en casos de su característico simplex (un ortoscheme particular con el diagrama de Coxeter ) es la construcción directa más básica de la tesseract posible. El característica 5 celdas del 4-cubo es una región fundamental del grupo de simetría que define el tesseract, el grupo que genera los politópicos B4. El simplex característico del tesseract directamente genera el tesseract a través de las acciones del grupo, reflexionándose en sus propias facetas ligadas (su paredes espejo).

Simetría equilátera radial

El radio largo (del centro al vértice) del tesseract es igual a la longitud de su borde; por lo tanto, su diagonal a través del centro (vértice al vértice opuesto) es la longitud de 2 aristas. Solo unos pocos politopos uniformes tienen esta propiedad, incluido el teseracto de cuatro dimensiones y el de 24 celdas, el cuboctaedro tridimensional y el hexágono bidimensional. En particular, el tesseract es el único hipercubo (aparte de un punto de dimensión 0) que es radialmente equilátero. El diámetro de vértice a vértice más largo de un hipercubo n-dimensional de longitud de borde unitaria es √n, entonces para el cuadrado es √2, para el cubo es √3, y solo para el teseracto es √4, exactamente 2 longitudes de borde.

Fórmulas

Prueba sin palabras de que un gráfico hipercubo no es plano usando los teoremas de Kuratowski o Wagner y encontrar o K₅ (top) or K_3,3 subgrafos

Para un teseracto con longitud de lado $s$ :

Hypervolume: ${displaystyle H=s^{4}}$
Volumen de superficie: ${displaystyle SV=8s^{3}}$
Cara diagonal: ${displaystyle d_{mathrm {2} }={sqrt {2}}s}$
Celular diagonal: ${displaystyle d_{mathrm {3} }={sqrt {3}}s}$
4-espacio diagonal: ${displaystyle d_{mathrm {4} }=2s}$

Como configuración

Esta matriz de configuración representa el teseracto. Las filas y columnas corresponden a vértices, aristas, caras y celdas. Los números diagonales indican cuántos elementos de cada elemento se encuentran en el teseracto completo. Los números no diagonales indican cuántos elementos de la columna se encuentran en o en el elemento de la fila. Por ejemplo, el 2 en la primera columna de la segunda fila indica que hay 2 vértices en (es decir, en los extremos de) cada borde; el 4 en la segunda columna de la primera fila indica que 4 aristas se encuentran en cada vértice.

${displaystyle {begin{bmatrix}{begin{matrix}16&4&6&4\2&32&3&3\4&4&24&2\8&12&6&8end{matrix}}end{bmatrix}}}$

Proyecciones

Es posible proyectar teseractos en espacios tridimensionales y bidimensionales, de manera similar a proyectar un cubo en un espacio bidimensional.

Envolturas de proyección paralelas del tesseract (cada célula se dibuja con diferentes caras de color, las células invertidas no se dibujan)

El dodecaedro rhombic forma el casco convexo de la proyección paralela del vértice-primero del tesseract. El número de vértices en las capas de esta proyección es 1 4 6 4 1—la cuarta fila en el triángulo de Pascal.

La proyección paralela cell-first del tesseract en el espacio tridimensional tiene una envoltura cúbica. Las celdas más cercanas y más lejanas se proyectan en el cubo y las seis celdas restantes se proyectan en las seis caras cuadradas del cubo.

La proyección paralela de cara primero del tesseract en el espacio tridimensional tiene una envoltura cúbica. Dos pares de celdas se proyectan hacia las mitades superior e inferior de este sobre, y las cuatro celdas restantes se proyectan hacia las caras laterales.

La proyección paralela borde primero del teseracto en el espacio tridimensional tiene una envoltura en forma de prisma hexagonal. Seis celdas se proyectan sobre prismas rómbicos, que se disponen en el prisma hexagonal de manera análoga a cómo las caras del cubo 3D se proyectan sobre seis rombos en una envoltura hexagonal bajo proyección de vértice primero. Las dos celdas restantes se proyectan sobre las bases del prisma.

La proyección paralela primero el vértice del teseracto en el espacio tridimensional tiene una envoltura dodecaédrica rómbica. Dos vértices del tesseract se proyectan al origen. Hay exactamente dos formas de dividir un dodecaedro rómbico en cuatro romboedros congruentes, dando un total de ocho romboedros posibles, cada uno de los cuales es un cubo proyectado del teseracto. Esta proyección es también la de máximo volumen. Un conjunto de vectores de proyección son u=(1,1,-1,-1), v=(-1,1,-1,1), w=(1,-1,-1,1).

Animación mostrando cada cubo individual dentro del B₄ Coxeter proyección de plano de la tesseract

Proyecciones ortoográficas
Coxeter avión	B₄	B₄ -- A₃	A₃
Gráfico
Simetría Dihedral	[8]	[4]	[4]
Coxeter avión	Otros	B₃ D₄ / A₂	B₂ D₃
Gráfico
Simetría Dihedral	[2]	[6]	[4]

Una proyección 3D de un tesseract realizando una rotación simple sobre un plano en espacio 4dimensional. El avión biseca la figura de la parte delantera izquierda a la derecha trasera y arriba a abajo.	Una proyección 3D de un tesseract que realiza una doble rotación sobre dos planos ortogonales en espacio dimensional.

3D Proyección de tres tesseracts con y sin rostros	Perspectiva con Eliminación oculta del volumen. La esquina roja es la más cercana en 4D y tiene 4 celdas cúbicas reunidas a su alrededor.

El tetraedro forma el casco convexo de la proyección central centrada en el vértice del tesseract. Se muestran cuatro de 8 celdas cúbicas. El 16o vértice se proyecta a la infinidad y los cuatro bordes a él no se muestran.	Proyección estereográfica (Las erecciones se proyectan sobre la 3sfera)

Proyección 3D estereocópica de un tesseract (vista paralela)
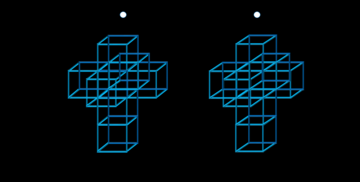Hipercubo desarmado estereoscopio 3D

Teselado

El teseracto, como todos los hipercubos, forma un teselado en el espacio euclidiano. El panal teseráctico autodual que consta de 4 teseractos alrededor de cada cara tiene el símbolo de Schläfli {4,3,3,4}. Por lo tanto, el teseracto tiene un ángulo diedro de 90°.

La simetría equilátera radial del teseracto hace que su teselación sea la única red cúbica regular centrada en el cuerpo de esferas de igual tamaño, en cualquier número de dimensiones.

Politopos y panales relacionados

El teseracto es el cuarto de una serie de hipercubos:

Proyecciones ortográficas de polígono Petrie

Serie de línea	Plaza	Cube	4-cube	5-cube	6-cube	7-cube	8-cube

El tesseract (8 celdas) es el tercero en la secuencia de 6 4 politopos regulares convexos (en orden de tamaño y complejidad).

Convexo regular 4-polytopes
Grupo de Symmetry	A4	B4		F4	H4
Nombre	5 celdas Hyper-tetrahedron 5 puntos	16 celdas Hyper-octahedron 8 puntos	8 celdas Hyper-cube 16 puntos	24 horas 24 puntos	600 celdas Hyper-icosahedron 120 puntos	120 celdas Hyper-dodecahedron 600 puntos
Símbolo Schläfli	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Espejos de hachater
Mirror dihedrals	π/3 π/3 π/3 π/2 π/2 π/2	π/3 π/3 π/4 π/2 π/2 π/2	π/4 π/3 π/3 π/2 π/2 π/2	π/3 π/4 π/3 π/2 π/2 π/2	π/3 π/3 π/5 π/2 π/2 π/2	π/5 π/3 π/3 π/2 π/2 π/2
Gráfico
Vertices	5 tetraedral	8 octadral	16 tetraedral	24 cúbicos	120 icosahedral	600 tetraedral
Edges	10 triangular	24 cuadrados	32 triangular	96 triangular	720 pentagonal	1200 triangular
Caras	10 triángulos	32 triángulos	24 plazas	96 triángulos	1200 triángulos	720 pentágonos
Celdas	5 tetrahedra	16 tetrahedra	8 cubos	24 octahedra	600 tetrahedra	120 dodecahedra
Tori	1 5-tetraedro	2 8-tetraedro	2 4-cubo	4 6-octaedron	20 30-tetraedro	12 10-dodecahedron
Inscritos	120 en 120 celdas	675 en 120 celdas	2 16 celdas	3 8 celdas	25 24 celdas	10 600 celdas
Grandes polígonos		2 π/2 cuadrados x 3	4 π/2 rectángulos x 3	4 π/3 hexágonos x 4	12 π/5 decagones x 6	50 π/15 dodecagons x 4
Petrie poligons	1 pentágono	1 octágono	2 octágonos	2 dodecagones	4 30-gones	20 30-gones
radio largo	$1$	$1$	$1$	$1$	$1$	$1$
Longitud del borde	${displaystyle {sqrt {tfrac {5}{2}}}approx 1.581}$	$sqrt{2} approx 1.414$	$1$	$1$	${displaystyle {tfrac {1}{phi }}approx 0.618}$	${displaystyle {tfrac {1}{phi ^{2}{sqrt {2}}}}approx 0.270}$
Breus corto	$tfrac{1}{4}$	${tfrac {1}{2}}$	${tfrac {1}{2}}$	${displaystyle {sqrt {tfrac {1}{2}}}approx 0.707}$	${displaystyle {sqrt {tfrac {phi ^{4}}{8}}}approx 0.926}$	${displaystyle {sqrt {tfrac {phi ^{4}}{8}}}approx 0.926}$
Zona	${displaystyle 10left({tfrac {5{sqrt {3}}}{8}}right)approx 10.825}$	${displaystyle 32left({sqrt {tfrac {3}{4}}}right)approx 27.713}$	$24$	${displaystyle 96left({sqrt {tfrac {3}{16}}}right)approx 41.569}$	${displaystyle 1200left({tfrac {sqrt {3}}{4phi ^{2}}}right)approx 198.48}$	${displaystyle 720left({tfrac {sqrt {25+10{sqrt {5}}}}{8phi ^{4}}}right)approx 90.366}$
Volumen	${displaystyle 5left({tfrac {5{sqrt {5}}}{24}}right)approx 2.329}$	${displaystyle 16left({tfrac {1}{3}}right)approx 5.333}$	$8$	${displaystyle 24left({tfrac {sqrt {2}}{3}}right)approx 11.314}$	${displaystyle 600left({tfrac {sqrt {2}}{12phi ^{3}}}right)approx 16.693}$	${displaystyle 120left({tfrac {15+7{sqrt {5}}}{4phi ^{6}{sqrt {8}}}}right)approx 18.118}$
4-Content	${displaystyle {tfrac {sqrt {5}}{24}}left({tfrac {sqrt {5}}{2}}right)^{4}approx 0.146}$	${displaystyle {tfrac {2}{3}}approx 0.667}$	$1$	$2$	${displaystyle {tfrac {{text{Short}}times {text{Vol}}}{4}}approx 3.863}$	${displaystyle {tfrac {{text{Short}}times {text{Vol}}}{4}}approx 4.193}$

Como duoprisma uniforme, el teseracto existe en una secuencia de duoprismas uniformes: {p}×{4}.

El teseracto regular, junto con el de 16 celdas, existe en un conjunto de 15 4 politopos uniformes con la misma simetría. El teseracto {4,3,3} existe en una secuencia de 4-politopos y panales regulares, {p,3,3} con figuras de vértice tetraédrico, {3,3}. El teseracto también está en una secuencia de 4 politopos regulares y panales, {4,3,p} con celdas cúbicas.

Ortogonal	Perspectiva

₄{4}₂, con 16 vértices y 8 4-edges, con los 8 4-edgos mostrados aquí como 4 cuadrados rojos y 4 azules

El politopeto complejo regular ₄{4}₂, , dentro $mathbb{C}^2$ tiene una representación real como un tesseract o 4-4 duoprismo en el espacio 4-dimensional. ₄{4}₂ tiene 16 vértices, y 8 4-edges. Su simetría es ₄[4]₂, orden 32. También tiene una construcción de simetría inferior, , o ₄{}₄Con simetría ₄[2]₄Orden 16. Esta es la simetría si los 4-edges rojos y azules se consideran distintos.

En la cultura popular

Desde su descubrimiento, los hipercubos de cuatro dimensiones han sido un tema popular en el arte, la arquitectura y la ciencia ficción. Los ejemplos notables incluyen:

"Y él construyó una Casa Crooked", historia de ciencia ficción de Robert Heinlein de 1940 con un edificio en la forma de una hipercubina cuadrienal. Este y el "Profesor No Sidido" de Martin Gardner, publicado en 1946, están entre los primeros en la ciencia ficción para introducir lectores a la banda Moebius, la botella Klein y el hipercubo (tesseract).
Crucifixión (Corpus Hypercubus), una pintura al óleo de 1954 por Salvador Dalí con un hipercubo de cuatro dimensiones se desarrolló en una cruz latina tridimensional.
El Grande Arche, monumento y edificio cerca de París, Francia, terminó en 1989. Según el ingeniero del monumento, Erik Reitzel, el Grande Arche fue diseñado para parecerse a la proyección de un hipercubo.
Fez, un videojuego donde uno juega un personaje que puede ver más allá de las dos dimensiones que otros personajes pueden ver, y debe utilizar esta habilidad para resolver puzzles de plataforma. Características "Dot", un tesseract que ayuda al jugador a navegar por el mundo y le dice cómo utilizar habilidades, ajustando el tema de ver más allá de la percepción humana del espacio dimensional conocido.

La palabra tesseract se adoptó más tarde para muchos otros usos en la cultura popular, incluso como recurso argumental en obras de ciencia ficción, a menudo con poca o ninguna conexión con el hipercubo de cuatro dimensiones de este artículo.. Ver Tesseract (desambiguación).

Contenido relacionado

Más resultados...