Teorema maestro (análisis de algoritmos)

En el análisis de algoritmos, el teorema maestro para las recurrencias de divide y vencerás proporciona un análisis asintótico (usando la notación O grande) para relaciones de recurrencia de tipos que ocurren en el análisis de muchas divisiones y conquistar algoritmos. El enfoque fue presentado por primera vez por Jon Bentley, Dorothea Blostein (de soltera Haken) y James B. Saxe en 1980, donde se describió como un "método unificador" para solucionar este tipo de recurrencias. El nombre "teorema maestro" fue popularizado por el libro de texto de algoritmos ampliamente utilizado Introducción a los algoritmos de Cormen, Leiserson, Rivest y Stein.

No todas las relaciones de recurrencia se pueden resolver con el uso de este teorema; sus generalizaciones incluyen el método Akra-Bazzi.

Introducción

Considere un problema que se puede resolver utilizando un algoritmo recursivo como el siguiente:

procedimiento p(input) x de tamaño n):
 si n Identificar una constante k:
Solve x directamente sin recursión
 más:
Crear a subproblemas de x, cada uno tiene tamaño n/bProcedimiento de llamada p recursivamente en cada subproblema
Combine los resultados de los subproblemas

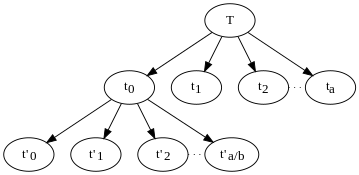
El algoritmo anterior divide el problema en una serie de subproblemas recursivamente, cada subproblema de tamaño n/b. Su árbol de solución tiene un nodo para cada llamada recursiva, siendo los niños de ese nodo las otras llamadas hechas de esa llamada. Las hojas del árbol son los casos de base de la recursión, los subproblemas (de tamaño inferior a kEso no se repite. El ejemplo anterior habría tenido a Nodos infantiles en cada nodo sin hojas. Cada nodo hace una cantidad de trabajo que corresponde al tamaño del subproblema n pasó a esa instancia de la llamada recursiva y dada por ${displaystyle f(n)}$. La cantidad total de trabajo realizado por todo el algoritmo es la suma del trabajo realizado por todos los nodos del árbol.

El tiempo de funcionamiento de un algoritmo como el p arriba en una entrada de tamaño n, generalmente denotado ${displaystyle T(n)}$, se puede expresar por la relación de recurrencia

${displaystyle T(n)=a;Tleft({frac {n}right)+f(n),}$

Donde ${displaystyle f(n)}$ es el momento de crear los subproblemas y combinar sus resultados en el procedimiento anterior. Esta ecuación puede sustituirse sucesivamente en sí misma y ampliarse para obtener una expresión de la cantidad total de trabajo realizado. El teorema maestro permite que muchas relaciones de recurrencia de esta forma se conviertan directamente a la anotación, sin hacer una expansión de la relación recursiva.

Forma genérica

El teorema maestro siempre produce ligaduras asintomáticamente ajustadas a recurrencias de algoritmos de división y conquista que dividen una entrada en subproblemas más pequeños de tamaños iguales, resuelven los subproblemas recursivamente, y luego combinan las soluciones de subproblema para dar una solución al problema original. El tiempo para tal algoritmo se puede expresar agregando el trabajo que realizan en el nivel superior de su recursión (para dividir los problemas en subproblemas y luego combinar las soluciones de subproblema) junto con el tiempo hecho en las llamadas recursivas del algoritmo. Si ${displaystyle T(n)}$ denota el tiempo total para el algoritmo en una entrada de tamaño ${displaystyle n}$, y ${displaystyle f(n)}$ denota la cantidad de tiempo tomado en el nivel superior de la recurrencia entonces el tiempo puede ser expresado por una relación recurrencia que toma el formulario:

${displaystyle T(n)=a;T!left({frac {n}right)+f(n)}$

Aquí. ${displaystyle n}$ es el tamaño de un problema de entrada, ${displaystyle a}$ es el número de subproblemas en la recursión, y ${displaystyle b}$ es el factor por el cual el tamaño del subproblema se reduce en cada llamada recursiva (b título1). Curiosamente, ${displaystyle a}$ y ${displaystyle b}$ no debe depender de ${displaystyle n}$. El teorema de abajo también supone que, como caso base para la recurrencia, ${displaystyle T(n)=Theta (1)}$ cuando ${displaystyle n}$ es menos que un límite ${displaystyle kappa }$, el tamaño de entrada más pequeño que conducirá a una llamada recursiva.

Las repeticiones de esta forma a menudo satisfacen uno de los tres siguientes regímenes, basados en cómo el trabajo para dividir/recombinar el problema ${displaystyle f(n)}$ relacionados con exponente crítico ${displaystyle ¿Qué?$. (La tabla de abajo utiliza la notación O grande estándar).

${displaystyle c_{operatorname {crit}=log ¿Por qué?$

Caso	Descripción	Estado ${displaystyle f(n)}$ en relación con ${displaystyle c_{fnMicrosoft}$, es decir. ${displaystyle log _{b}a}$	Maestro Teorema	Ejemplos notables
1	Trabajar para dividir/recombinar un problema está encadenado por subproblemas. i.e. the recursion tree is leaf-heavy	Cuando ${displaystyle f(n)=O(n^{c}}$ Donde ${displaystyle c$ (Arribado por un polinomio menos exponente)	Entonces... ${displaystyle T(n)=Theta left(n^{c_{operatorname {crit}}right)}}$ (El término de división no aparece; la estructura del árbol recurrente domina.)	Si ${displaystyle b=a^{2}$ y ${displaystyle f(n)=O(n^{1/2-epsilon }}$, entonces ${displaystyle T(n)=Theta (n^{1/2})}$.
2	Trabajar para dividir/recombinar un problema es comparable a los subproblemas.	Cuando ${displaystyle f(n)=Theta (n^{c_{operatorname {crit}log ^{k}n)}$ para un ${displaystyle kgeq 0}$ (recorrido por el polinomio de costos críticos, tiempos cero o más opcionales ${displaystyle log }$s)	Entonces... ${displaystyle T(n)=Theta left(n^{c_{operatorname {crit}log ^{k+1}nright)}$ (El límite es el término de división, donde el tronco es aumentado por una sola potencia.)	Si ${displaystyle b=a^{2}$ y ${displaystyle f(n)=Theta (n^{1/2})}$, entonces ${displaystyle T(n)=Theta (n^{1/2}log n)}$. Si ${displaystyle b=a^{2}$ y ${displaystyle f(n)=Theta (n^{1/2}log n)}$, entonces ${displaystyle T(n)=Theta (n^{1/2}log ^{2}n)}$.
3	Trabajar para dividir/recombinar un problema domina subproblemas. Es decir, el árbol de la recursión es arraigado.	Cuando ${displaystyle f(n)=Omega (n^{c}}$ Donde ${displaystyle c título.$ (más bajo contenido por un polinomio de mayor crecimiento)	... esto no produce necesariamente nada. Además, si ${displaystyle afleft({frac {n}right)leq kf(n)}$ para alguna constante ${displaystyle k won1}$ y suficientemente grandes ${displaystyle n}$ (a menudo llamado el condición de regularidad) entonces el total está dominado por el término de división ${displaystyle f(n)}$: ${displaystyle Tleft(nright)=Theta left(f(n)right)}$	Si ${displaystyle b=a^{2}$ y ${displaystyle f(n)=Omega (n^{1/2+epsilon)}$ y la condición de regularidad sostiene, entonces ${displaystyle T(n)=Theta (f(n)}$.

Una extensión útil de Case 2 maneja todos los valores de ${displaystyle k}$:

Caso	Estado ${displaystyle f(n)}$ en relación con ${displaystyle c_{fnMicrosoft}$, es decir. ${displaystyle log _{b}a}$	Maestro Teorema	Ejemplos notables
2a	Cuando ${displaystyle f(n)=Theta (n^{c_{operatorname {crit}log ^{k}n)}$ para cualquier ${displaystyle k]$	Entonces... ${displaystyle T(n)=Theta left(n^{c_{operatorname {crit}log ^{k+1}nright)}$ (El límite es el término de división, donde el tronco es aumentado por una sola potencia.)	Si ${displaystyle b=a^{2}$ y ${displaystyle f(n)=Theta (n^{1/2}/log ^{1/2}n)}$, entonces ${displaystyle T(n)=Theta (n^{1/2}log ^{1/2}n)}$.
2b	Cuando ${displaystyle f(n)=Theta (n^{c_{operatorname {crit}log ^{k}n)}$ para ${displaystyle k=-1}$	Entonces... ${displaystyle T(n)=Theta left(n^{c_{operatorname {crit}log log nright)}$ (El límite es el término de división, donde el log reciprocal es reemplazado por un tronco iterado.)	Si ${displaystyle b=a^{2}$ y ${displaystyle f(n)=Theta (n^{1/2}/log n)}$, entonces ${displaystyle T(n)=Theta (n^{1/2}log log n)}$.
2c	Cuando ${displaystyle f(n)=Theta (n^{c_{operatorname {crit}log ^{k}n)}$ para cualquier ${displaystyle k ordenados-1}$	Entonces... ${displaystyle T(n)=Theta left(n^{c_{operatorname {crit}}right)}}$ (El límite es el término de división, donde el tronco desaparece.)	Si ${displaystyle b=a^{2}$ y ${displaystyle f(n)=Theta (n^{1/2}/log ^{2}n)}$, entonces ${displaystyle T(n)=Theta (n^{1/2})}$.

Ejemplos

Ejemplo del caso 1

${displaystyle T(n)=8Tleft({frac {n}right)+1000n^{2}$

Como se puede ver en la fórmula anterior:

${displaystyle a=8,,b=2,,f(n)=1000n^{2}$Así que

${displaystyle f(n)=Oleft(n^{c}right)}$, donde ${displaystyle c=2}$

A continuación, vemos si cumplimos la condición del caso 1:

${displaystyle log _{b}a=log ¿Qué?$.

Se deduce del primer caso del teorema maestro que

${displaystyle T(n)=Theta left(n^{log _{b}a}right)= Theta left (n^{3}right)}$

(Este resultado es confirmado por la solución exacta de la relación de recurrencia, que es ${displaystyle T(n)=1001n^{3}-1000n^{2}$, suponiendo ${displaystyle T(1)=1}$).

Ejemplo de caso 2

${displaystyle T(n)=2Tleft({frac {n}right)+10n}$

Como podemos ver en la fórmula anterior, las variables obtienen los siguientes valores:

${displaystyle a=2,,b=2,,c=1,,f(n)=10n}$

${displaystyle f(n)=Theta left(n^{c}log ^{k}nright)}$ Donde ${displaystyle c=1,k=0}$

A continuación, vemos si cumplimos la condición del caso 2:

${displaystyle log _{b}a=log #2=1}$, y por lo tanto, c y ${displaystyle log _{b}a}$ son iguales

Así que sigue del segundo caso del teorema maestro:

${displaystyle T(n)=Theta left(n^{log _{b}a}log ^{k+1}nright)= Theta left(n^{1}log ^{1}nright)= Theta left(nlog nright)}$

Así la relación de recurrencia dada ${displaystyle T(n)}$ estaba dentro ${displaystyle Theta (nlog n)}$.

(Este resultado es confirmado por la solución exacta de la relación de recurrencia, que es ${displaystyle T(n)=n+10nlog _{2}n}$, suponiendo ${displaystyle T(1)=1}$).

Ejemplo 3

${displaystyle T(n)=2Tleft({frac {n}right)+n^{2}$

Como podemos ver en la fórmula anterior, las variables obtienen los siguientes valores:

${displaystyle a=2,,b=2,,f(n)=n^{2}$

${displaystyle f(n)=Omega left(n^{c}right)}$, donde ${displaystyle c=2}$

A continuación, vemos si satisfacemos el caso 3 condición:

${displaystyle log _{b}a=log #2=1}$, y por lo tanto, sí, ${displaystyle c]log _{b}a}$

La condición de regularidad también se cumple:

${displaystyle 2left {frac}{4}right)leq kn^{2}}$, elegir ${displaystyle k=1/2}$

Así se deduce del tercer caso del teorema maestro:

${displaystyle Tleft(nright)=Theta left(f(n)right)=Theta left(n^{2}right). }$

Así la relación de recurrencia dada ${displaystyle T(n)}$ estaba dentro ${displaystyle Theta (n^{2})}$, que cumple con el ${displaystyle f(n)}$ de la fórmula original.

(Este resultado es confirmado por la solución exacta de la relación de recurrencia, que es ${displaystyle T(n)=2n^{2}-n}$, suponiendo ${displaystyle T(1)=1}$.)

Ecuaciones inadmisibles

Las siguientes ecuaciones no se pueden resolver utilizando el teorema maestro:

• ${displaystyle T(n)=2^{n}Tleft({frac {n}right)+n^{n}$

  a no es una constante; el número de subproblemas debe ser fijo

• ${displaystyle T(n)=2Tleft({frac {n}right)+{frac {n}{log n}}}$

  diferencia no polinómica entre ${displaystyle f(n)}$ y ${displaystyle n^{log _{b}a}$ (véase infra; versión ampliada se aplica)

• ${displaystyle T(n)=0.5Tleft({frac {n}right)+n}$

  ${displaystyle a won1}$ no puede tener menos de un sub problema

• ${displaystyle T(n)=64Tleft({frac {n}right)-n^{2}log n}$

  ${displaystyle f(n)}$, que es el tiempo de combinación, no es positivo

• ${displaystyle T(n)=Tleft({frac {n}right)+n(2-cos n)}$

  caso 3 pero violación de la regularidad.

En el segundo ejemplo inadmisible anterior, la diferencia entre ${displaystyle f(n)}$ y ${displaystyle n^{log _{b}a}$ se puede expresar con la relación ${displaystyle {frac {f(n)}{n^{log ¿Qué? ¿Qué? {n}{nlog No. {1}{log n}}$. Está claro que ${displaystyle {frac {fn}{g} {epsilon} {fn}} {fn}} {fn} {fn}}}}}}} {fnK}}}}}} {fnK}}}} {fnK}}}}}}}}}}}}}}} {fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\\\\\\\fn}\\\\\\\\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\$ para cualquier constante ${displaystyle epsilon }$. Por lo tanto, la diferencia no es polinomio y la forma básica del Teorema Maestro no se aplica. La forma extendida (caso 2b) se aplica, dando la solución ${displaystyle T(n)=Theta (nlog log n)}$.

Aplicación a algoritmos comunes

Algoritm	Relación de repetición	Hora de correr	Comentario
Búsqueda binaria	${displaystyle T(n)=Tleft({frac {n}right)+O(1)}$	${displaystyle O(log n)}$	Apply Master theorem case ${displaystyle c=log _{b}a}$, donde ${displaystyle a=1,b=2,c=0,k=0}$
Traversal de árbol binario	${displaystyle T(n)=2Tleft({frac {n}right)+O(1)}$	${displaystyle O(n)}$	Apply Master theorem case ${displaystyle c madelog _{b}a}$ Donde ${displaystyle a=2,b=2,c=0}$
Búsqueda óptima de matriz clasificada	${displaystyle T(n)=2Tleft({frac {n}right)+O(log n)}$	${displaystyle O(n)}$	Aplica el teorema Akra–Bazzi para ${displaystyle p=1}$ y ${displaystyle g(u)=log(u)}$ para llegar ${displaystyle Theta (2n-log n)}$
Merge tipo	${displaystyle T(n)=2Tleft({frac {n}right)+O(n)}$	${displaystyle O(nlog n)}$	Apply Master theorem case ${displaystyle c=log _{b}a}$, donde ${displaystyle a=2,b=2,c=1,k=0}$