Tensión superficial

Flujo de agua de lluvia de un recipiente. Entre las fuerzas que gobiernan la formación de gotas: tensión superficial, cohesión, fuerza Van der Waals, meseta-Rayleigh inestabilidad.

Tensión superficial es la tendencia de las superficies líquidas en reposo a contraerse hasta la mínima superficie posible. La tensión superficial es lo que permite que los objetos con una densidad más alta que el agua, como hojas de afeitar e insectos (por ejemplo, zancudos de agua), floten en la superficie del agua sin sumergirse ni siquiera parcialmente.

En las interfases líquido-aire, la tensión superficial resulta de la mayor atracción de las moléculas líquidas entre sí (debido a la cohesión) que entre las moléculas del aire (debido a la adhesión).

Hay dos mecanismos principales en juego. Una es una fuerza hacia adentro sobre las moléculas de la superficie que hace que el líquido se contraiga. La segunda es una fuerza tangencial paralela a la superficie del líquido. Esta fuerza tangencial generalmente se denomina tensión superficial. El efecto neto es que el líquido se comporta como si su superficie estuviera cubierta por una membrana elástica estirada. Pero esta analogía no debe llevarse demasiado lejos ya que la tensión en una membrana elástica depende de la cantidad de deformación de la membrana mientras que la tensión superficial es una propiedad inherente del líquido–aire o líquido –interfaz de vapor.

Debido a la atracción relativamente alta de las moléculas de agua entre sí a través de una red de enlaces de hidrógeno, el agua tiene una tensión superficial más alta (72,8 milinewtons (mN) por metro a 20 °C) que la mayoría de los demás líquidos. La tensión superficial es un factor importante en el fenómeno de la capilaridad.

La tensión superficial tiene la dimensión de fuerza por unidad de longitud o de energía por unidad de área. Los dos son equivalentes, pero al referirse a la energía por unidad de área, es común usar el término energía superficial, que es un término más general en el sentido de que se aplica también a los sólidos.

En la ciencia de los materiales, la tensión superficial se utiliza para la tensión superficial o la energía superficial.

Causas

Diagrama de las fuerzas cohesivas sobre moléculas de un líquido

Debido a las fuerzas cohesivas, una molécula ubicada lejos de la superficie es atraída por igual en todas las direcciones por las moléculas líquidas vecinas, lo que resulta en una fuerza neta de cero. Las moléculas en la superficie no tienen las mismas moléculas en todos los lados y, por lo tanto, son atraídas hacia adentro. Esto crea algo de presión interna y obliga a las superficies líquidas a contraerse al mínimo.

También hay una tensión paralela a la superficie en la interfaz líquido-aire que resistirá una fuerza externa, debido a la naturaleza cohesiva de las moléculas de agua.

Las fuerzas de atracción que actúan entre moléculas del mismo tipo se denominan fuerzas cohesivas, mientras que las que actúan entre moléculas de diferente tipo se denominan fuerzas adhesivas. El equilibrio entre la cohesión del líquido y su adhesión al material del recipiente determina el grado de humectación, el ángulo de contacto y la forma del menisco. Cuando domina la cohesión (específicamente, la energía de adhesión es menos de la mitad de la energía de cohesión) la humectación es baja y el menisco es convexo en una pared vertical (como ocurre con el mercurio en un recipiente de vidrio). Por otro lado, cuando domina la adhesión (energía de adhesión más de la mitad de la energía de cohesión) la humectación es alta y el menisco similar es cóncavo (como en el agua en un vaso).

La tensión superficial es responsable de la forma de las gotas de líquido. Aunque se deforman fácilmente, las gotitas de agua tienden a adoptar una forma esférica debido al desequilibrio de las fuerzas cohesivas de la capa superficial. En ausencia de otras fuerzas, las gotas de prácticamente todos los líquidos serían aproximadamente esféricas. La forma esférica minimiza la necesaria "tensión de la pared" de la capa superficial según la ley de Laplace.

Una gota de agua en un damask. La tensión superficial es lo suficientemente alta como para evitar ver el textil

Otra forma de ver la tensión superficial es en términos de energía. Una molécula en contacto con una vecina se encuentra en un estado de energía más bajo que si estuviera sola. Las moléculas interiores tienen tantos vecinos como sea posible, pero a las moléculas de los límites les faltan vecinos (en comparación con las moléculas interiores) y, por lo tanto, tienen una energía más alta. Para que el líquido minimice su estado de energía, se debe minimizar el número de moléculas límite de mayor energía. El número minimizado de moléculas límite da como resultado un área de superficie mínima. Como resultado de la minimización del área superficial, una superficie asumirá la forma más suave posible (la prueba matemática de que las formas 'suaves' minimizan el área superficial se basa en el uso de la ecuación de Euler-Lagrange). Dado que cualquier curvatura en la forma de la superficie da como resultado un área mayor, también resultará una energía más alta.

Física

Unidades físicas

La tensión superficial, representada por el símbolo γ (alternativamente σ o T), se mide en fuerza por unidad de longitud. Su unidad SI es newton por metro, pero también se usa la unidad cgs de dina por centímetro. Por ejemplo,

$${displaystyle gamma =1~mathrm {frac {yn}{cm} =1~mathrm {frac}{cm^{2}} =1~mathrm {frac {10^{-7},mcdot N}{10^{-4},m^{2}} =0.001~mathrm {frac {N}{m} =0.001~mathrm {frac} {J}{m^{2}}}}$$

Definición

Este diagrama ilustra la fuerza necesaria para aumentar la superficie. Esta fuerza es proporcional a la tensión superficial.

La tensión superficial se puede definir en términos de fuerza o energía.

En términos de fuerza

La tensión superficial γ de un líquido es la fuerza por unidad de longitud. En la ilustración de la derecha, el marco rectangular, compuesto por tres lados inamovibles (negros) que forman una "U" forma, y un cuarto lado móvil (azul) que se puede deslizar hacia la derecha. La tensión superficial empujará la barra azul hacia la izquierda; la fuerza F requerida para sostener el lado móvil es proporcional a la longitud L del lado inmóvil. Por lo tanto, la relación F/L depende únicamente de las propiedades intrínsecas del líquido (composición, temperatura, etc.), no en su geometría. Por ejemplo, si el marco tuviera una forma más complicada, la relación F/L, con L la longitud del lado móvil y F se encuentra que la fuerza requerida para evitar que se deslice es la misma para todas las formas. Por lo tanto, definimos la tensión superficial como

$${displaystyle gamma ={frac {F}{2L}.}$$

En términos de energía

La tensión superficial γ de un líquido es la relación entre el cambio en la energía del líquido y el cambio en la superficie área del líquido (que condujo al cambio de energía). Esto se puede relacionar fácilmente con la definición anterior en términos de fuerza: si F es la fuerza requerida para detener el lado de comenzando a deslizarse, entonces esta es también la fuerza que mantendría el lado en el estado de deslizamiento a una velocidad constante (según la Segunda Ley de Newton). Pero si el lado se mueve hacia la derecha (en la dirección en que se aplica la fuerza), entonces el área superficial del líquido estirado aumenta mientras que la fuerza aplicada realiza trabajo sobre el líquido. Esto significa que al aumentar el área superficial aumenta la energía de la película. El trabajo realizado por la fuerza F al mover el lado por la distancia Δx es W = FΔx; al mismo tiempo, el área total de la película aumenta en ΔA = 2LΔx (el factor de 2 está aquí porque el líquido tiene dos lados, dos superficies). Por lo tanto, multiplicando tanto el numerador como el denominador de γ = 1 /2 F/L por Δx, obtenemos

$${displaystyle gamma ={frac {F}{2L}={frac} {FDelta x}{2LDelta x}={frac} {W}{fn} Delta A}}$$

Efectos

Agua

Se pueden observar varios efectos de la tensión superficial con el agua corriente:

• 

  A. Agua abatida en una hoja

• 

  B. Agua goteando de un grifo

• 

  C. Los conflictos de agua permanecen en la parte superior del líquido debido a la tensión superficial

• 

  D. Lámpara de lava con interacción entre líquidos disimilares: agua y cera líquida

• 

  E. Foto que muestra el fenómeno de "teares de vino".

Tensoactivos

La tensión superficial es visible en otros fenómenos comunes, especialmente cuando se usan surfactantes para disminuirla:

• Las burbujas de jabón tienen áreas de superficie muy grandes con muy poca masa. Las burbujas en agua pura son inestables. Sin embargo, la adición de surfactantes puede tener un efecto estabilizador en las burbujas (ver efecto Marangoni). Tenga en cuenta que los surfactantes realmente reducen la tensión superficial del agua por un factor de tres o más.
• Las emulsiones son un tipo de coloides en el que la tensión superficial juega un papel. Pequeños fragmentos de aceite suspendidos en agua pura se reunirán espontáneamente en masas mucho más grandes. Pero la presencia de un surfactante proporciona una disminución de la tensión superficial, lo que permite la estabilidad de gotas de aceite minutos en el grueso del agua (o viceversa).

Curvatura superficial y presión

Fuerza de tensión superficial actuando en un pequeño parche (diferencial) de superficie. δθ_x y δθ_Sí. indicar la cantidad de curva sobre las dimensiones del parche. Equilibrar las fuerzas de tensión con presión conduce a la ecuación Young-Laplace

Si ninguna fuerza actúa normal a una superficie tensionada, la superficie debe permanecer plana. Pero si la presión en un lado de la superficie difiere de la presión en el otro lado, la diferencia de presión multiplicada por el área de la superficie da como resultado una fuerza normal. Para que las fuerzas de tensión superficial cancelen la fuerza debida a la presión, la superficie debe ser curva. El diagrama muestra cómo la curvatura de la superficie de un pequeño parche de superficie conduce a un componente neto de las fuerzas de tensión superficial que actúan de manera normal al centro del parche. Cuando todas las fuerzas están equilibradas, la ecuación resultante se conoce como la ecuación de Young-Laplace:

$${displaystyle Delta p=gamma left({frac {1}{x}}+{frac} {1} {R_{y}} {}}} {}}}} {} {}} {}}} {}}}}} {}}}}}}} {}}} {}}}} {}} {} {} {}}} {}} {}}} {}}}}}}}} {}}}} {}}}}}} {}}}}}}}}} {}}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}} {}}}}}} {}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}$$

• Δp es la diferencia de presión, conocida como la presión de Laplace.
• γ es tensión superficial.
• R_x y R_Sí. son radios de curvatura en cada uno de los ejes que son paralelos a la superficie.

La cantidad entre paréntesis en el lado derecho es de hecho (el doble) de la curvatura media de la superficie (dependiendo de la normalización). Las soluciones a esta ecuación determinan la forma de las gotas de agua, charcos, meniscos, pompas de jabón y todas las demás formas determinadas por la tensión superficial (como la forma de las impresiones que los pies de un zancudo de agua hacen en la superficie de un estanque). La siguiente tabla muestra cómo aumenta la presión interna de una gota de agua con un radio decreciente. Para gotas no muy pequeñas el efecto es sutil, pero la diferencia de presión se vuelve enorme cuando el tamaño de las gotas se acerca al tamaño molecular. (En el límite de una sola molécula, el concepto pierde sentido).

Objetos flotantes

Corte transversal de una aguja flotando en la superficie del agua. F_w es el peso y F_s son las fuerzas resultantes de la tensión superficial.

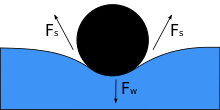
Cuando se coloca un objeto sobre un líquido, su peso F_w deprime la superficie, y si la tensión superficial y la fuerza hacia abajo se igualan, entonces se equilibra con las fuerzas de tensión superficial en ambos lados F_s, que son paralelas a la superficie del agua en los puntos donde entra en contacto con el objeto. Tenga en cuenta que un pequeño movimiento en el cuerpo puede hacer que el objeto se hunda. A medida que disminuye el ángulo de contacto, disminuye la tensión superficial. Los componentes horizontales de las dos flechas F_s apuntan en direcciones opuestas, por lo que se anulan entre sí, pero los componentes verticales apuntan en la misma dirección y, por lo tanto, se suman para equilibrar F_w. La superficie del objeto no debe ser humectable para que esto suceda, y su peso debe ser lo suficientemente bajo para que la tensión superficial lo soporte. Si m denota la masa de la aguja y g la aceleración debida a la gravedad, tenemos

$${displaystyle F_{mathrm {w}=2F_{mathrm {s}sin theta quad Leftrightarrow quad mg=2gamma Lsin theta }$$

Superficie líquida

Superficie mínima

Encontrar la forma de la superficie mínima delimitada por un marco de forma arbitraria usando medios estrictamente matemáticos puede ser una tarea abrumadora. Sin embargo, al hacer el marco con alambre y sumergirlo en una solución de jabón, aparecerá una superficie localmente mínima en la película de jabón resultante en cuestión de segundos.

La razón de esto es que la diferencia de presión a través de una interfaz de fluido es proporcional a la curvatura media, como se ve en la ecuación de Young-Laplace. Para una película de jabón abierta, la diferencia de presión es cero, por lo que la curvatura media es cero y las superficies mínimas tienen la propiedad de curvatura media cero.

Ángulos de contacto

La superficie de cualquier líquido es una interfaz entre ese líquido y algún otro medio. La superficie superior de un estanque, por ejemplo, es una interfaz entre el agua del estanque y el aire. La tensión superficial, entonces, no es una propiedad del líquido solamente, sino una propiedad de la interfaz del líquido con otro medio. Si hay un líquido en un recipiente, además de la interfaz líquido/aire en su superficie superior, también hay una interfaz entre el líquido y las paredes del recipiente. La tensión superficial entre el líquido y el aire suele ser diferente (mayor) que su tensión superficial con las paredes de un recipiente. Y donde las dos superficies se encuentran, su geometría debe ser tal que todas las fuerzas se equilibren.

Fuerzas en punto de contacto mostradas para ángulo de contacto superior a 90° (izquierda) y menos de 90° (derecha)

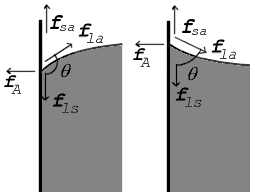
Donde las dos superficies se encuentran, forman un ángulo de contacto, θ, que es el ángulo que forma la tangente a la superficie con la superficie sólida. Tenga en cuenta que el ángulo se mide a través del líquido, como se muestra en los diagramas anteriores. El diagrama de la derecha muestra dos ejemplos. Las fuerzas de tensión se muestran para la interfaz líquido-aire, la interfaz líquido-sólido y la interfaz sólido-aire. El ejemplo de la izquierda es donde la diferencia entre la tensión superficial líquido-sólido y sólido-aire, γ_ls − γ _sa, es menor que la tensión superficial líquido-aire, γ_la, pero sin embargo es positivo, es decir

$${displaystyle gamma _{mathrm {la}gamma _{mathrm {ls} ¿Qué?$$

En el diagrama, tanto la fuerza vertical como la horizontal deben cancelarse exactamente en el punto de contacto, conocido como equilibrio. El componente horizontal de f_la es cancelado por la fuerza adhesiva, f_A.

$${displaystyle f_{mathrm {A}=f_{mathrm {la}sin theta }$$

Sin embargo, el equilibrio de fuerzas más revelador es el de la dirección vertical. La componente vertical de f_la debe cancelar exactamente la diferencia de fuerzas a lo largo de la superficie sólida, f_ls − f_sa.

$${displaystyle f_{mathrm} }-f_{mathrm {sa} }=-f_{mathrm {la}cos theta }$$

Dado que las fuerzas son directamente proporcionales a sus respectivas tensiones superficiales, también tenemos:

$${displaystyle gamma _{mathrm {ls} }-gamma _{mathrm {sa} }=-gamma _{mathrm {la} }cos theta }$$

dónde

• γ_Is es la tensión de superficie líquida-sólida,
• γ_la es la tensión de superficie líquida-aire,
• γ_sa es la tensión de la superficie del aire sólido,
• Silencio es el ángulo de contacto, donde un menisco concave tiene ángulo de contacto inferior a 90° y un menisco convexo tiene ángulo de contacto superior a 90°.

Esto significa que aunque la diferencia entre la tensión superficial líquido-sólido y sólido-aire, γ_ls − γ _sa, es difícil de medir directamente, se puede inferir de la tensión superficial líquido-aire, γ_la, y el ángulo de contacto de equilibrio, θ, que es una función de los ángulos de contacto de avance y retroceso fácilmente medibles (ver artículo principal ángulo de contacto).

Esta misma relación existe en el diagrama de la derecha. Pero en este caso vemos que debido a que el ángulo de contacto es menor a 90°, la diferencia de tensión superficial líquido-sólido/sólido-aire debe ser negativa:

$${displaystyle gamma _{mathrm {la} {]} Confío0gamma _{mathrm {ls} }-gamma _{mathrm {se}$$

Ángulos de contacto especiales

Observe que en el caso especial de una interfase agua-plata donde el ángulo de contacto es igual a 90°, la diferencia de tensión superficial líquido-sólido/sólido-aire es exactamente cero.

Otro caso especial es donde el ángulo de contacto es exactamente 180°. El agua con teflón especialmente preparado se acerca a esto. El ángulo de contacto de 180° ocurre cuando la tensión superficial líquido-sólido es exactamente igual a la tensión superficial líquido-aire.

$${displaystyle gamma _{mathrm {la} }=gamma _{mathrm {ls} }-gamma _{mathrm {sa} ################################################################################################################################################################################################################################################################$$

Líquido en un tubo vertical

Diagrama de un barómetro de mercurio

Un barómetro de mercurio de estilo antiguo consta de un tubo de vidrio vertical de aproximadamente 1 cm de diámetro parcialmente lleno de mercurio y con un vacío (llamado vacío de Torricelli) en el volumen vacío (ver diagrama a la derecha). Observe que el nivel de mercurio en el centro del tubo es más alto que en los bordes, lo que hace que la superficie superior del mercurio tenga forma de cúpula. El centro de masa de toda la columna de mercurio estaría ligeramente más bajo si la superficie superior del mercurio fuera plana en toda la sección transversal del tubo. Pero la parte superior en forma de cúpula le da un área de superficie ligeramente menor a toda la masa de mercurio. De nuevo, los dos efectos se combinan para minimizar la energía potencial total. Tal forma de superficie se conoce como menisco convexo.

Consideramos el área superficial de toda la masa de mercurio, incluida la parte de la superficie que está en contacto con el vidrio, porque el mercurio no se adhiere al vidrio en absoluto. Entonces, la tensión superficial del mercurio actúa sobre toda su superficie, incluso donde está en contacto con el vidrio. Si en lugar de vidrio, el tubo fuera de cobre, la situación sería muy diferente. El mercurio se adhiere agresivamente al cobre. Entonces, en un tubo de cobre, el nivel de mercurio en el centro del tubo será más bajo que en los bordes (es decir, sería un menisco cóncavo). En una situación en la que el líquido se adhiere a las paredes de su recipiente, consideramos que la parte de la superficie del fluido que está en contacto con el recipiente tiene tensión superficial negativa. Luego, el fluido trabaja para maximizar el área de la superficie de contacto. Entonces, en este caso, aumentar el área en contacto con el recipiente disminuye en lugar de aumentar la energía potencial. Esa disminución es suficiente para compensar el aumento de energía potencial asociado con el levantamiento del fluido cerca de las paredes del recipiente.

Ilustración de ascenso capilar y caída. Ángulo rojo=contacto inferior a 90°; azul=contacto superior a 90°

Si un tubo es lo suficientemente angosto y la adherencia del líquido a sus paredes es lo suficientemente fuerte, la tensión superficial puede hacer que el líquido suba por el tubo en un fenómeno conocido como acción capilar. La altura a la que se eleva la columna viene dada por la ley de Jurín:

$${displaystyle h={frac {2gamma _{mathrm {la} }cos theta } {rho gr}$$

dónde

• h es la altura que el líquido se levanta,
• γ_la es la tensión de superficie líquida-aire,
• *** es la densidad del líquido,
• r es el radio del capilar,
• g es la aceleración debido a la gravedad,
• Silencio es el ángulo de contacto descrito anteriormente. Si Silencio es mayor de 90°, como con mercurio en un recipiente de vidrio, el líquido será deprimido en lugar de levantarse.

Charcos en una superficie

Curva de perfil del borde de un charco donde el ángulo de contacto es de 180°. La curva es dada por la fórmula:

$${displaystyle ¿Qué? {}} {}}} {}}} {}}} {}}}}}} {}}}} {}}}}} {}}}}}}}}}}} {}}}}}} {}}} {}}}}}}}}} {}}}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}} {}}}}}}}}}} {}} {}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$$

Donde ${fnMiembro H=2{sqrt {gmma}/{grho}}}}}$

Los pequeños charcos de agua en una superficie limpia lisa tienen un espesor perceptible.

Verter mercurio sobre una hoja plana horizontal de vidrio da como resultado un charco que tiene un espesor perceptible. El charco se extenderá solo hasta el punto en que tenga un grosor de poco menos de medio centímetro, y no más delgado. De nuevo, esto se debe a la acción de la fuerte tensión superficial del mercurio. La masa líquida se aplana porque lleva la mayor cantidad de mercurio al nivel más bajo posible, pero la tensión superficial, al mismo tiempo, actúa para reducir el área superficial total. El resultado del compromiso es un charco de un espesor casi fijo.

La misma demostración de tensión superficial se puede hacer con agua, agua de cal o incluso solución salina, pero solo sobre una superficie hecha de una sustancia a la que no se adhiere el agua. La cera es una sustancia de este tipo. El agua vertida sobre una superficie de cera lisa, plana y horizontal, digamos una lámina de vidrio encerada, se comportará de manera similar al mercurio vertido sobre el vidrio.

El espesor de un charco de líquido sobre una superficie cuyo ángulo de contacto es de 180° viene dado por:

$${fnMicroc} {gamma} } {grho }}$$

dónde

• h es la profundidad del charco en centímetros o metros.
• γ es la tensión superficial del líquido en dines por centímetro o newtons por metro.
• g es la aceleración debido a la gravedad y es igual a 980 cm/s² 9.8 m/s²
• *** es la densidad del líquido en gramos por centímetro cúbico o kilogramos por metro cúbico

Ilustración de cómo el ángulo de contacto inferior conduce a la reducción de la profundidad del charco

En realidad, el grosor de los charcos será ligeramente inferior al previsto por la fórmula anterior porque muy pocas superficies tienen un ángulo de contacto de 180° con cualquier líquido. Cuando el ángulo de contacto es inferior a 180°, el espesor viene dado por:

$${displaystyle h={sqrt {frac {2gamma _{mathrm {la}left(1-cos theta right)}{grho }}}}$$

Para mercurio sobre vidrio, γ_Hg = 487 dyn/cm, ρ_Hg = 13,5 g/cm³ y θ = 140°, lo que da h_Hg = 0,36 cm. Para agua sobre parafina a 25 °C, γ = 72 dyn/cm, ρ = 1,0 g/cm³, y θ = 107° que da h_H2O = 0,44 cm.

La fórmula también predice que cuando el ángulo de contacto es de 0°, el líquido se extenderá en una capa microdelgada sobre la superficie. Se dice que dicha superficie es totalmente humectable por el líquido.

La fragmentación de los flujos en gotas

Romper una corriente alargada de agua en gotas debido a la tensión superficial.

En la vida cotidiana, todos observamos que un chorro de agua que sale de un grifo se descompone en gotitas, sin importar cuán suavemente salga el chorro del grifo. Esto se debe a un fenómeno llamado inestabilidad Plateau-Rayleigh, que es enteramente una consecuencia de los efectos de la tensión superficial.

La explicación de esta inestabilidad comienza con la existencia de pequeñas perturbaciones en la corriente. Estos siempre están presentes, sin importar qué tan fluido sea el flujo. Si las perturbaciones se resuelven en componentes sinusoidales, encontramos que algunos componentes crecen con el tiempo mientras que otros decaen con el tiempo. Entre los que crecen con el tiempo, algunos crecen a un ritmo más rápido que otros. Si un componente decae o crece, y qué tan rápido crece es completamente una función de su número de onda (una medida de cuántos picos y valles por centímetro) y los radios de la corriente cilíndrica original.

Galería

• 

  Romper una hoja de agua en movimiento rebotando de una cuchara.

• 

  Foto de flujo de agua adherida a una mano. La tensión superficial crea la hoja de agua entre el flujo y la mano.

• 

  Una burbuja de jabón equilibra las fuerzas de tensión superficial contra la presión neumática interna.

• 

  La tensión superficial evita que una moneda se hunda: la moneda es indiscutiblemente más densa que el agua, por lo que debe estar desplazando un volumen mayor que el suyo propio para el equilibrio de masa.

• 

  Una moneda de aluminio flota en la superficie del agua a 10 °C. Cualquier peso adicional caería la moneda al fondo.

• 

  Una margarita. La totalidad de la flor está por debajo del nivel de la superficie libre (inisturbed). El agua se eleva suavemente alrededor de su borde. La tensión superficial evita que el agua displace el aire entre los pétalos y posiblemente sumerge la flor.

• 

  Un clip de papel metálico flota sobre el agua. Por lo general, varios pueden añadirse cuidadosamente sin desbordamiento de agua.

• 

  Un clip metálico flotando en el agua. Una parrilla delante de la luz ha creado las 'líneas de contorno' que muestran la deformación en la superficie del agua causada por el clip de papel metálico.

Termodinámica

Teorías termodinámicas de la tensión superficial

J.W. Gibbs desarrolló la teoría termodinámica de la capilaridad basada sobre la idea de superficies de discontinuidad. Gibbs consideró el caso de una superficie matemática aguda que se coloca en algún lugar dentro de la interfaz física microscópicamente borrosa que existe entre dos sustancias homogéneas. Al darse cuenta de que la elección exacta de la ubicación de la superficie era algo arbitraria, lo dejó flexible. Puesto que la interfaz existe en equilibrio térmico y químico con las sustancias que la rodean (con temperaturas T y potenciales químicos μ_i), Gibbs consideró el caso donde la superficie puede tener exceso de energía, exceso de entropía y exceso de partículas, encontrando la función de energía libre natural en este caso para ser ${displaystyle U-TS-mu - No. - No.$, una cantidad más tarde llamada como el gran potencial y dado el símbolo ${displaystyle Omega }$.

La colocación de Gibbs de una superficie matemática precisa en una interfaz física borrosa.

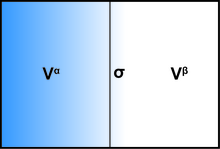
Considerando un subvolumen dado ${displaystyle V}$ que contiene una superficie de discontinuidad, el volumen se divide por la superficie matemática en dos partes A y B, con volúmenes ${displaystyle V_{text{A}}$ y ${displaystyle V_{text{B}}$, con ${displaystyle V=V_{text{A}+V_{text{B}$ exactamente. Ahora, si las dos partes A y B eran fluidos homogéneos (con presiones) ${displaystyle ¿Qué?$, ${displaystyle ¿Qué?$) y permaneció perfectamente homogéneo derecho hasta el límite matemático, sin ningún efecto superficial, el gran potencial total de este volumen sería simplemente ${displaystyle - ¿Qué?$. Los efectos superficiales del interés son una modificación a esto, y todos pueden ser recogidos en un término de energía libre de superficie ${displaystyle Omega _{text{S}}$ por lo que el gran potencial total del volumen se convierte en:

$${displaystyle Omega - Sí. Omega.$$

Para superficies lo suficientemente macroscópicas y suavemente curvadas, la energía libre de la superficie debe ser simplemente proporcional al área de la superficie:

$${displaystyle Omega _{text{S}=gamma A,}$$

${displaystyle gamma }$

${displaystyle A}$

Como se indicó anteriormente, ello implica el trabajo mecánico necesario para aumentar la superficie A es dW = γ dA, asumiendo que los volúmenes de cada lado no cambian. La termodinámica requiere que para los sistemas mantenidos con potencial químico constante y temperatura, todos los cambios espontáneos de estado se acompañan de una disminución de esta energía libre ${displaystyle Omega }$, es decir, un aumento de la entropía total teniendo en cuenta el posible movimiento de energía y partículas de la superficie a los fluidos circundantes. De esto es fácil entender por qué disminuir la superficie de una masa de líquido es siempre espontáneo, siempre que no se acopla a ningún otro cambio energético. De ahí que para aumentar la superficie, se debe añadir cierta cantidad de energía.

Gibbs y otros científicos han luchado con la arbitrariedad en la colocación microscópica exacta de la superficie. Para superficies microscópicas con curvaturas muy estrechas, no es correcto asumir que la tensión superficial es independiente del tamaño, y temas como la longitud Tolman entran en juego. Para una superficie de tamaño macroscópico (y superficies planas), la colocación de la superficie no tiene un efecto significativo en γ sin embargo tiene un efecto muy fuerte en los valores de la entropía superficial, densidades de masa superficial y energía interna superficial, que son los derivados parciales de la función de tensión superficial ${displaystyle gamma (T,mu _{1},mu _{2},cdots)}$.

Gibbs enfatizó que para los sólidos, la energía superficial libre puede ser completamente diferente del estrés superficial (lo que él llamó tensión superficial): la energía superficial libre es el trabajo requerido para formar la superficie, mientras que la superficie El estrés es el trabajo requerido para estirar la superficie. En el caso de una interfase de dos fluidos, no hay distinción entre formación y estiramiento porque los fluidos y la superficie recuperan completamente su naturaleza cuando se estira la superficie. Para un sólido, estirar la superficie, incluso elásticamente, da como resultado una superficie fundamentalmente cambiada. Además, la tensión superficial en un sólido es una cantidad direccional (un tensor de tensión), mientras que la energía superficial es escalar.

Quince años después de Gibbs, J.D. van der Waals desarrolló la teoría de los efectos capilares basados en la hipótesis de una variación continua de la densidad. Añadió a la densidad energética el término ${displaystyle c(nabla rho)}{2}$ Donde c es el coeficiente capilares y *** es la densidad. Para el multifase equilibria, los resultados del enfoque van der Waals prácticamente coinciden con la fórmula Gibbs, pero para modelar el dinámica el enfoque van der Waals es mucho más conveniente. La energía capilar de van der Waals ahora se utiliza ampliamente en los modelos de campo de fase de flujos multifase. Tales términos también se descubren en la dinámica de gases no equilibrios.

Termodinámica de burbujas

La presión dentro de una burbuja esférica ideal puede derivarse de consideraciones termodinámicas de energía libre. La energía libre anterior se puede escribir como:

$${displaystyle Omega =-Delta PV_{text{A}-p_{B}V+gamma A}$$

${displaystyle Delta P=p_{text{A}-p_{text{B}}$

${displaystyle V_{text{A}}$

$${displaystyle Delta P,dV_{text{A}=gamma,dA}$$

Para una burbuja esférica, el volumen y el área de superficie están dados simplemente por

$${displaystyle V_{text{A}={tfrac {4}{3}pi} R^{3}quad rightarrow quad dV_{text{A}=4pi R^{2},dR,}$$

$${displaystyle A=4pi R^{2}quad rightarrow quad dA=8pi R,dR.}$$

Sustituyendo estas relaciones en la expresión anterior, encontramos

$${displaystyle Delta P={frac {2} {R}gamma}$$

Influencia de la temperatura

Temperatura dependencia de la tensión superficial entre las fases de líquido y vapor de agua pura

Temperatura dependencia de la tensión superficial de benceno

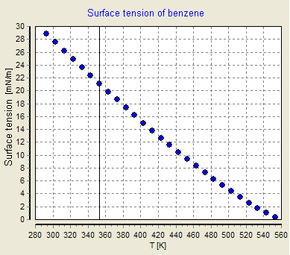
La tensión superficial depende de la temperatura. Por esa razón, cuando se da un valor para la tensión superficial de una interfase, se debe indicar explícitamente la temperatura. La tendencia general es que la tensión superficial disminuye con el aumento de la temperatura, alcanzando un valor de 0 a la temperatura crítica. Para más detalles, consulte la regla de Eötvös. Solo existen ecuaciones empíricas para relacionar la tensión superficial y la temperatura:

• Eötvös:
  $${displaystyle gamma V^{2/3}=k(T_{mathrm {C}-T).}$$

  
  Aquí. V es el volumen molar de una sustancia, T_C es la temperatura crítica y k es una constante válida para casi todas las sustancias. Un valor típico es k = 2.1×10⁻⁷J K⁻¹ mol^−2.3. Para el agua se puede utilizar más V = 18 ml/mol y T_C = 647 K (374 °C). Una variante en Eötvös es descrita por Ramay y Shields:
  $${displaystyle gamma V^{2/3}=kleft(T_{mathrm {C}-T-6right)}$$

  
  donde el offset de temperatura de 6 K proporciona la fórmula con un mejor ajuste a la realidad a temperaturas inferiores.
• Guggenheim-Katayama:
  $${displaystyle gamma =gamma ^{circ }left(1-{frac {T}{mathrm {C}}}right)} {n}$$

  
  γ° es una constante para cada líquido y n es un factor empírico, cuyo valor es 11/9 para líquidos orgánicos. Esta ecuación también fue propuesta por van der Waals, quien propuso además que γ° podría ser dada por la expresión
  $${displaystyle K_{2}T_{mathrm {C}{1/3}P_{mathrm {C}} {2/3}$$

  
  Donde K₂ es una constante universal para todos los líquidos, y P_C es la presión crítica del líquido (aunque experimentos posteriores encontrados K₂ variar en algún grado de un líquido a otro).

Tanto Guggenheim–Katayama como Eötvös tienen en cuenta el hecho de que la tensión superficial llega a 0 a la temperatura crítica, mientras que Ramay y Shields no logran igualar la realidad en este punto final.

Influencia de la concentración de soluto

Los solutos pueden tener diferentes efectos sobre la tensión superficial dependiendo de la naturaleza de la superficie y del soluto:

• Poco o ningún efecto, por ejemplo el azúcar en el agua sometidaair, la mayoría de compuestos orgánicos en aceite/aire
• Aumentar la tensión superficial, la mayoría de las sales inorgánicas en el agua
• Cambio no monotónico, la mayoría de ácidos inorgánicos en el agua
• Disminuir la tensión superficial progresivamente, como en la mayoría de los anfilos, por ejemplo, alcoholes en el agua
• Disminuir la tensión superficial hasta cierta concentración crítica, y ningún efecto después: surfactantes que forman células

Lo que complica el efecto es que un soluto puede existir en una concentración diferente en la superficie de un solvente que en su mayor parte. Esta diferencia varía de una combinación soluto-disolvente a otra.

La isoterma de Gibbs establece que:

$${displaystyle Gamma =-{frac {1}}left({frac {partial gamma }{partial ln C}}right)_{T,P}}$$

• . se conoce como concentración superficial, representa el exceso de soluto por área unidad de la superficie sobre lo que estaría presente si la concentración de vracs prevalecía hasta la superficie. Tiene unidades de mol/m²
• C es la concentración de la sustancia en la solución a granel.
• R es la constante del gas y T la temperatura

Se toman ciertas suposiciones en su deducción, por lo tanto, la isoterma de Gibbs solo se puede aplicar a soluciones ideales (muy diluidas) con dos componentes.

Influencia del tamaño de partícula en la presión de vapor

La relación Clausius-Clapeyron conduce a otra ecuación también atribuida a Kelvin, como la ecuación de Kelvin. Explica por qué, debido a la tensión superficial, la presión de vapor de las pequeñas gotas de líquido en suspensión es mayor que la presión de vapor estándar de ese mismo líquido cuando la interfase es plana. Es decir, cuando un líquido está formando pequeñas gotas, la concentración de equilibrio de su vapor en su entorno es mayor. Esto surge porque la presión en el interior de la gota es mayor que en el exterior.

$${displaystyle P_{mathrm {}{mathrm {fnMicrosoft} }=P_{mathrm {v} {circ }e^{V2gamma - Sí.$$

Molecules en la superficie de una pequeña gota (izquierda) tienen, en promedio, menos vecinos que los de una superficie plana (derecha). Por lo tanto están ligados más débilmente a la gota que las moléculas de superficie plana.

• P_v° es la presión de vapor estándar para ese líquido a esa temperatura y presión.
• V es el volumen molar.
• R es la constante del gas
• r_k es el radio Kelvin, el radio de las gotas.

El efecto explica la sobresaturación de los vapores. En ausencia de sitios de nucleación, se deben formar pequeñas gotas antes de que puedan evolucionar a gotas más grandes. Esto requiere una presión de vapor muchas veces la presión de vapor en el punto de transición de fase.

Esta ecuación también se utiliza en la química de catalizadores para evaluar la mesoporosidad de los sólidos.

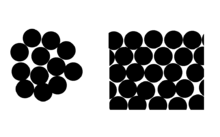
El efecto se puede ver en términos del número promedio de vecinos moleculares de las moléculas de la superficie (ver diagrama).

La tabla muestra algunos valores calculados de este efecto para el agua en diferentes tamaños de gota:

El efecto se vuelve claro para tamaños de gota muy pequeños, ya que una gota de 1 nm de radio tiene alrededor de 100 moléculas en su interior, que es una cantidad lo suficientemente pequeña como para requerir un análisis de mecánica cuántica.

Métodos de medición

Debido a que la tensión superficial se manifiesta en varios efectos, ofrece varios caminos para su medición. El método óptimo depende de la naturaleza del líquido que se mide, las condiciones bajo las cuales se mide su tensión y la estabilidad de su superficie cuando se deforma. Un instrumento que mide la tensión superficial se llama tensiómetro.

• Método de anillo Du Noüy: El método tradicional utilizado para medir la tensión superficial o interfacial. Las propiedades de tejido de la superficie o la interfaz tienen poca influencia en esta técnica de medición. Se mide el tirón máximo ejercido en el anillo por la superficie.
• Método de la placa Wilhelmy: Un método universal especialmente adecuado para comprobar la tensión superficial a largo plazo. Una placa vertical del perímetro conocido se une a un equilibrio, y la fuerza debido al desgaste se mide.
• Método de gota giratoria: Esta técnica es ideal para medir tensiones interfaciales bajas. El diámetro de una gota dentro de una fase pesada se mide mientras ambos se giran.
• Método de gota colgante: Esta técnica puede medir la tensión superficial e interfacial, incluso a temperaturas y presiones elevadas. La geometría de una gota se analiza ópticamente. Para el colgante baja el diámetro máximo y la relación entre este parámetro y el diámetro a la distancia del diámetro máximo del ápice de gota se ha utilizado para evaluar los parámetros de tamaño y forma para determinar la tensión superficial.
• Método de presión de burbujas (método de jaeger): Técnica de medición para determinar la tensión superficial a corta edad. Se mide la presión máxima de cada burbuja.
• Método de volumen de gota: Un método para determinar la tensión interfacial como función de la edad de interfaz. El líquido de una densidad se bombea en un segundo líquido de una densidad diferente y se mide el tiempo entre gotas producidas.
• Método de subida capilar: El final de un capilar está inmerso en la solución. La altura en la que la solución alcanza dentro del capilar está relacionada con la tensión superficial por la ecuación discutida a continuación.]]]
• Método estalagmométrico: Un método de ponderación y lectura de una gota de líquido.
• Método de gota de sesil: Un método para determinar la tensión superficial y la densidad colocando una gota en un sustrato y midiendo el ángulo de contacto (ver técnica de gota Sessile).
• Método Du Noüy-Padday: Una versión minimizada del método Du Noüy utiliza una aguja de metal de diámetro pequeño en lugar de un anillo, en combinación con un microbalance de alta sensibilidad para grabar el máximo tirador. La ventaja de este método es que los volúmenes de muestras muy pequeños (abajo de pocas decenas de microlitros) se pueden medir con muy alta precisión, sin la necesidad de corregir para la flotabilidad (para una aguja o más bien, varilla, con geometría adecuada). Además, la medición se puede realizar muy rápidamente, mínimamente en unos 20 segundos.
• Frecuencia vibracional de gotas levitadas: La frecuencia natural de oscilaciones vibracionales de gotas levitadas magnéticamente se ha utilizado para medir la tensión superficial de superfluidas ⁴Él. Este valor se estima en 0,375 dina/cm T = 0 K.
• oscilaciones resonantes de gota de líquido esférico y hemisférico: La técnica se basa en la medición de la frecuencia resonante de gotas colgante esféricas y hemisféricas impulsadas en oscilaciones por un campo eléctrico modulado. La tensión superficial y la viscosidad se pueden evaluar a partir de las curvas resonantes obtenidas.
• Método de rebote: Este método se basa en la levitación aerodinámica con un diseño de boquillas. Después de dejar caer una gota levitada en una plataforma, la muestra deforma y rebota hacia atrás, oscilando en el aire medio mientras intenta minimizar su superficie. A través de este comportamiento de oscilación, se puede medir la tensión superficial y la viscosidad del líquido.
• Por teléfono inteligente: Algunos teléfonos inteligentes se pueden utilizar para medir la tensión superficial de un líquido transparente. El método se basa en la medición de la longitud de onda de ondas capilares de frecuencia conocida. El smartphone se coloca encima de una taza con el líquido. Luego las ondas capilares vibro-motor del smartphone (a través de la taza) en la superficie del líquido, que son capturadas por la cámara del smartphone.

Valores

Tabla de datos

Tensión superficial del agua

La tensión superficial del agua líquida pura en contacto con su vapor ha sido dada por IAPWS como

$${displaystyle gamma _{text{w}=235.8left(1-{frac {T}{T_{text{C}}}right)}{1.256}left[1-0.625left(1-{frac] Bueno...$$

donde tanto T como la temperatura crítica T< sub>C = 647,096 K se expresan en kelvin. La región de validez de toda la curva de saturación vapor-líquido, desde el punto triple (0,01 °C) hasta el punto crítico. También proporciona resultados razonables cuando se extrapola a condiciones metaestables (sobreenfriadas), hasta al menos -25 °C. Esta formulación fue adoptada originalmente por IAPWS en 1976 y se ajustó en 1994 para ajustarse a la Escala Internacional de Temperatura de 1990.

La incertidumbre de esta formulación se da en todo el rango de temperatura por IAPWS. Para temperaturas inferiores a 100 °C, la incertidumbre es de ±0,5 %.

Tensión superficial del agua de mar

Nayar et al. datos de referencia publicados para la tensión superficial del agua de mar en el rango de salinidad de 20 ≤ S ≤ 131 g/kg y un rango de temperatura de 1 ≤ t ≤ 92 °C a presión atmosférica. El rango de temperatura y salinidad abarca tanto el rango oceanográfico como el rango de condiciones encontradas en las tecnologías de desalinización térmica. La incertidumbre de las mediciones varió de 0,18 a 0,37 mN/m, siendo la incertidumbre media de 0,22 mN/m.

Nayar et al. correlacionó los datos con la siguiente ecuación

$${displaystyle gamma _{mathrm {sw} }=gamma _{mathrm {w}left(1+3.766times 10^{-4}S+2.347times 10^{-6}Stright)}$$

La Asociación Internacional para las Propiedades del Agua y el Vapor (IAPWS) ha adoptado esta correlación como una guía estándar internacional.

Notas explicativas