Sistema de coordenadas polares

Puntos en el sistema de coordenadas polares con polo O y eje polar L. En verde, el punto con coordenadas radiales 3 y coordenadas angulares 60 grados o (3,60°). En azul, el punto (4,210°).

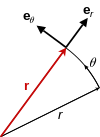
En matemáticas, el sistema de coordenadas polares es un sistema de coordenadas bidimensional en el que cada punto en un plano está determinado por una distancia desde un punto de referencia y un ángulo desde una dirección de referencia. El punto de referencia (análogo al origen de un sistema de coordenadas cartesianas) se denomina polo, y el rayo del polo en la dirección de referencia es el eje polar. La distancia desde el polo se llama coordenada radial, distancia radial o simplemente radio, y el ángulo se llama coordenada angular, ángulo polar o azimut. Los ángulos en notación polar generalmente se expresan en grados o radianes (2π rad es igual a 360°).

Grégoire de Saint-Vincent y Bonaventura Cavalieri introdujeron los conceptos de forma independiente a mediados del siglo XVII, aunque el término actual "coordenadas polares" ha sido atribuida a Gregorio Fontana en el siglo XVIII. La motivación inicial para la introducción del sistema polar fue el estudio del movimiento circular y orbital.

Las coordenadas polares son más apropiadas en cualquier contexto donde el fenómeno que se está considerando está ligado inherentemente a la dirección y la longitud desde un punto central en un plano, como espirales. Los sistemas físicos planos con cuerpos que se mueven alrededor de un punto central, o los fenómenos que se originan en un punto central, suelen ser más simples e intuitivos de modelar utilizando coordenadas polares.

El sistema de coordenadas polares se extiende a tres dimensiones de dos maneras: los sistemas de coordenadas cilíndricas y esféricas.

Historia

Hipparchus

Los conceptos de ángulo y radio ya eran utilizados por los pueblos antiguos del primer milenio antes de Cristo. El astrónomo y astrólogo griego Hipparchus (190-120 a. C.) creó una tabla de funciones de cuerda que proporciona la longitud de la cuerda para cada ángulo, y hay referencias a su uso de coordenadas polares para establecer posiciones estelares. En Sobre las espirales, Arquímedes describe la espiral de Arquímedes, una función cuyo radio depende del ángulo. El trabajo griego, sin embargo, no se extendió a un sistema de coordenadas completo.

Desde el siglo VIII d. C. en adelante, los astrónomos desarrollaron métodos para aproximar y calcular la dirección a La Meca (qibla) y su distancia desde cualquier lugar de la Tierra. Desde el siglo IX en adelante, utilizaron trigonometría esférica y métodos de proyección de mapas para determinar estas cantidades con precisión. El cálculo es esencialmente la conversión de las coordenadas polares ecuatoriales de La Meca (es decir, su longitud y latitud) a sus coordenadas polares (es decir, su qibla y distancia) en relación con un sistema cuyo meridiano de referencia es el gran círculo a través de la ubicación dada y la Tierra. 39;s polos y cuyo eje polar es la línea que pasa por la ubicación y su punto antípoda.

Hay varios relatos de la introducción de coordenadas polares como parte de un sistema de coordenadas formal. La historia completa del tema se describe en Origin of Polar Coordinates del profesor de Harvard Julian Lowell Coolidge. Grégoire de Saint-Vincent y Bonaventura Cavalieri introdujeron los conceptos de forma independiente a mediados del siglo XVII. Saint-Vincent escribió sobre ellos en privado en 1625 y publicó su trabajo en 1647, mientras que Cavalieri publicó el suyo en 1635 con una versión corregida que apareció en 1653. Cavalieri utilizó por primera vez las coordenadas polares para resolver un problema relacionado con el área dentro de una espiral de Arquímedes. Posteriormente, Blaise Pascal utilizó coordenadas polares para calcular la longitud de los arcos parabólicos.

En Method of Fluxions (escrito en 1671, publicado en 1736), Sir Isaac Newton examinó las transformaciones entre coordenadas polares, a las que se refirió como la "séptima manera; Para espirales" y otros nueve sistemas de coordenadas. En la revista Acta Eruditorum (1691), Jacob Bernoulli utilizó un sistema con un punto en una línea, llamado polo y eje polar respectivamente. Las coordenadas se especificaron por la distancia desde el polo y el ángulo desde el eje polar. El trabajo de Bernoulli se extendió a encontrar el radio de curvatura de las curvas expresadas en estas coordenadas.

El término actual coordenadas polares se ha atribuido a Gregorio Fontana y fue utilizado por escritores italianos del siglo XVIII. El término apareció en inglés en la traducción de George Peacock de 1816 del Differential and Integral Calculus de Lacroix. Alexis Clairaut fue el primero en pensar en coordenadas polares en tres dimensiones, y Leonhard Euler fue el primero en desarrollarlas.

Convenios

Una rejilla polar con varios ángulos, aumentando en orientación en sentido contrario y etiquetado en grados

La coordenada radial a menudo se denota por r o ρ, y la coordenada angular por φ, θ o t. La coordenada angular se especifica como φ según la norma ISO 31-11. Sin embargo, en la literatura matemática, el ángulo a menudo se denota con θ.

Los ángulos en notación polar generalmente se expresan en grados o radianes (2π rad equivale a 360°). Los grados se usan tradicionalmente en navegación, topografía y muchas disciplinas aplicadas, mientras que los radianes son más comunes en matemáticas y física matemática.

El ángulo φ se define para comenzar en 0° desde una dirección de referencia, y para aumentar para rotaciones en la dirección de las manecillas del reloj (cw) o en sentido contrario a las manecillas del reloj (ccw). Por ejemplo, en matemáticas, la dirección de referencia generalmente se dibuja como un rayo desde el polo horizontalmente hacia la derecha, y el ángulo polar aumenta a ángulos positivos para rotaciones a la izquierda, mientras que en navegación (rumbo, rumbo) se dibuja el rumbo 0°. verticalmente hacia arriba y el ángulo aumenta para rotaciones en sentido horario. Los ángulos polares disminuyen hacia valores negativos para rotaciones en las orientaciones opuestas respectivamente.

Singularidad de las coordenadas polares

Agregar cualquier número de vueltas completas (360°) a la coordenada angular no cambia la dirección correspondiente. De manera similar, cualquier coordenada polar es idéntica a la coordenada con el componente radial negativo y la dirección opuesta (sumando 180 ° al ángulo polar). Por lo tanto, un mismo punto (r, φ) se puede expresar con un número infinito de coordenadas polares diferentes (r, φ + n × 360°) y (−r, φ + 180° + n × 360°) = (−r, φ + (2n + 1) × 180°), donde n es un número entero arbitrario. Además, el polo mismo se puede expresar como (0, φ) para cualquier ángulo φ.

Cuando se necesita una representación única para cualquier punto además del polo, se suele limitar r a números positivos (r > 0) y φ al intervalo [0, 360°) o al intervalo (−180°, 180°], que en radianes son [0, 2π) o (−π, π]</ otra convención, en referencia al codominio habitual de la función arctan, es permitir valores reales arbitrarios distintos de cero del componente radial y restringir el ángulo polar a (−90°, 90°]. En todos los casos, se debe elegir un acimut único para el polo (r = 0), por ejemplo, φ = 0.

Conversión entre coordenadas polares y cartesianas

Un diagrama que ilustra la relación entre coordenadas polares y cartesianas.

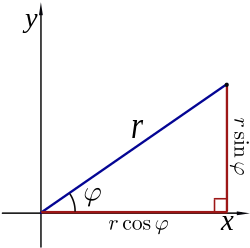
Las coordenadas polares r y φ se pueden convertir a las coordenadas cartesianas x y y usando el funciones trigonométricas seno y coseno:

x=r#⁡ ⁡ φ φ ,Sí.=rpecado⁡ ⁡ φ φ .{displaystyle {begin{aligned}x limit=rcos varphi\y pulsa=rsin varphi.end{aligned}}}

Las coordenadas cartesianas x e y se pueden convertir a coordenadas polares r y φ con r ≥ 0 y φ en el intervalo (−π, π] por:

r=x2+Sí.2=hipotético⁡ ⁡ ()x,Sí.)φ φ =atan2⁡ ⁡ ()Sí.,x),{displaystyle {begin{aligned}r {x^{2}+y^{2}}=operatorname {hypot} (x,y)\varphi &=operatorname {atan2} (y,x),end{aligned}}

0\arctan left({frac {y}{x}}right)+pi &{mbox{if }}x<0{mbox{ and }}ygeq 0\arctan left({frac {y}{x}}right)-pi &{mbox{if }}x<0{mbox{ and }}y0\-{frac {pi }{2}}&{mbox{if }}x=0{mbox{ and }}yatan2⁡ ⁡ ()Sí.,x)={}arctan⁡ ⁡ ()Sí.x)six■0arctan⁡ ⁡ ()Sí.x)+π π six.0ySí.≥ ≥ 0arctan⁡ ⁡ ()Sí.x)− − π π six.0ySí..0π π 2six=0ySí.■0− − π π 2six=0ySí..0indefinidossix=0ySí.=0.{displaystyle operatorname {atan2} (y,x)={begin{cases}arctan left({frac {y}{x}right) ########### {frac {y}{x}right)+pi &mbox{if }x {0{mbox{ and }ygeq 0\\arctan left({frac {y}{x}}}}right)-pi > {mbox} {mboxmbox} {mbox}{0} {mbox} {}}mboxm}m}m}} {c}mbox} {c}c}c} {c}c}c}c}c}c}c}c}c}cc}cc}cc}c}cc}cccccc}c}c}c}c}cccc}cc}c}cc}c}c} }{2}} {mbox{if}x=0{mbox{ y }y {fn\fnfn\fn\fnMicroc {pi} }{2} {mbox{if} }x=0{mbox{ and }}y 0{text{undefinido} {mbox{if }x=0{mbox{ and }y=0end{cases}}}

0\arctan left({frac {y}{x}}right)+pi &{mbox{if }}x<0{mbox{ and }}ygeq 0\arctan left({frac {y}{x}}right)-pi &{mbox{if }}x<0{mbox{ and }}y0\-{frac {pi }{2}}&{mbox{if }}x=0{mbox{ and }}y

Si r se calcula primero como se indicó anteriormente, entonces esta fórmula para φ se puede establecer de manera más simple usando la función arcocoseno:

Números complejos

Una ilustración de un número complejo z trazado en el plano complejo

Una ilustración de un número complejo trazado en el plano complejo usando la fórmula de Euler

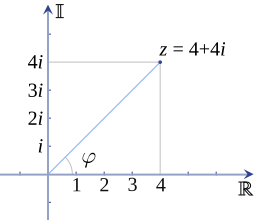
Cada número complejo se puede representar como un punto en el plano complejo y, por lo tanto, se puede expresar especificando las coordenadas cartesianas del punto (llamada forma rectangular o cartesiana) o las coordenadas polares del punto (llamada forma polar). El número complejo z se puede representar en forma rectangular como

z=x+iSí.{displaystyle z=x+iy}

z=r()#⁡ ⁡ φ φ +ipecado⁡ ⁡ φ φ ){displaystyle z=r(cos varphi +isin varphi)}

z=reiφ φ =rexp⁡ ⁡ iφ φ .{displaystyle z=re^{ivarphi }=rexp ivarphi.}

z=rcis⁡ ⁡ φ φ =r∠ ∠ φ φ .{displaystyle z=roperatorname {mathrm {cis} varphi =rangle varphi.}

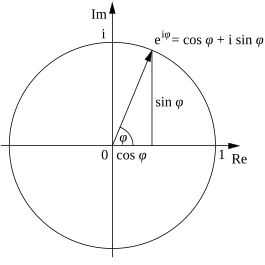
Para las operaciones de multiplicación, división, exponenciación y extracción de raíces de números complejos, generalmente es mucho más simple trabajar con números complejos expresados en forma polar en lugar de forma rectangular. De las leyes de la exponenciación:

Multiplicación

r0eiφ φ 0r1eiφ φ 1=r0r1ei()φ φ 0+φ φ 1){displaystyle r_{0}e^{ivarphi ¿Qué? ## {1}=r_{0}r_{1}e^{ileft(varphi) _{0}+varphi _{1}right)}

División

r0eiφ φ 0r1eiφ φ 1=r0r1ei()φ φ 0− − φ φ 1){displaystyle {frac {f}e^{ivarphi} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} ¿Qué? {fnh} {fnh} {fnh00}}}} {cH00}} {cHFF}}} {cHFF}}}}} {cH00}}}}}}}} {cH00}}}}}} {ccH}}}}} {cH00}}}}}}}}}}}}}}}}}}}}}} {\\\\\cH}}}}}}}}}}}} {cH}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\cH _{0}-varphi - Sí.

Exposición (fórmula de De Moivre)

()reiφ φ )n=rneinφ φ {displaystyle left(re^{ivarphi }right)} {n}=r^{n}e^{invarphi }

Extracción de raíz (raíz principal)

reiφ φ n=rneiφ φ n{displaystyle {sqrt}{re^{ivarphi {fn} {fn} {fn} {fn}}} {fn}}}} {fn}}}}} {fn}}}}}} {fn}}}}}}}}}} {fn}}}} {\fn}}}}}}}} {\\\\\\fn}\\\\\\fn}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\shn}\shn}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Ecuación polar de una curva

Una curva en el plano cartesiano se puede mapear en coordenadas polares. En esta animación, Sí.=pecado⁡ ⁡ ()6x)+2{displaystyle y=sin(6x)+2} se mapea en r=pecado⁡ ⁡ ()6Silencio Silencio )+2{displaystyle r=sin(6theta)+2}. Haga clic en la imagen para obtener detalles.

La ecuación que define una curva algebraica expresada en coordenadas polares se conoce como ecuación polar. En muchos casos, dicha ecuación puede especificarse simplemente definiendo r como una función de φ. La curva resultante consta entonces de puntos de la forma (r(φ), φ) y puede considerarse como el gráfico de la función polar r. Tenga en cuenta que, en contraste con las coordenadas cartesianas, la variable independiente φ es la segunda entrada en el par ordenado.

Se pueden deducir diferentes formas de simetría a partir de la ecuación de una función polar r:

• Si r() -φ) r()φ) la curva será simétrica sobre el rayo horizontal (0°/180°);
• Si r()π − φ) r()φ) será simétrico sobre el rayo vertical (90°/270°):
• Si r()φ − α) = r()φ) será simétrico rotacionalmente por α en sentido de reloj y en sentido contrario sobre el polo.

Debido a la naturaleza circular del sistema de coordenadas polares, muchas curvas pueden describirse mediante una ecuación polar bastante simple, mientras que su forma cartesiana es mucho más compleja. Entre las más conocidas de estas curvas se encuentran la rosa polar, la espiral de Arquímedes, la lemniscata, la limaçon y la cardioide.

Para el círculo, la línea y la rosa polar a continuación, se entiende que no hay restricciones en el dominio y el rango de la curva.

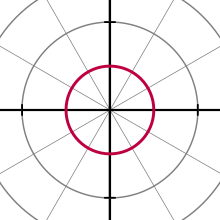
Círculo

Un círculo con ecuación r()φ) = 1

La ecuación general para un círculo con un centro en ()r0,γ γ ){displaystyle (r_{0},gamma)} y radio a es

r2− − 2rr0#⁡ ⁡ ()φ φ − − γ γ )+r02=a2.{displaystyle r^{2}-2rr_{0}cos(varphi -gamma)+r_{0}=a^{2}

Esto se puede simplificar de varias maneras, para adaptarse a casos más específicos, como la ecuación

r()φ φ )=a{displaystyle r(varphi)=a}

Cuando r₀ = a o el origen se encuentra en el círculo, el la ecuación se convierte en

r=2a#⁡ ⁡ ()φ φ − − γ γ ).{displaystyle r=2acos(varphi -gamma).}

En el caso general, la ecuación se puede resolver para r, dando

r=r0#⁡ ⁡ ()φ φ − − γ γ )+a2− − r02pecado2⁡ ⁡ ()φ φ − − γ γ ){displaystyle.

Línea

Radiales (aquellas que atraviesan el poste) están representadas por la ecuación

φ φ =γ γ ,{displaystyle varphi =gamma}

γ γ {displaystyle gamma }

φ φ =arctan⁡ ⁡ m{displaystyle varphi =arctan m}

m{displaystyle m}

φ φ =γ γ {displaystyle varphi =gamma }

()r0,γ γ ){displaystyle (r_{0},gamma)}

r()φ φ )=r0sec⁡ ⁡ ()φ φ − − γ γ ).{displaystyle r(varphi)=r_{0}sec(varphi -gamma).}

De lo contrario declarado ()r0,γ γ ){displaystyle (r_{0},gamma)} es el punto en el que el tangente intersecciona el círculo imaginario del radio r0{displaystyle R_{0}

Rosa polar

Una rosa polar con ecuación r()φ) = 2 pecado 4φ

Una rosa polar es una curva matemática que parece una flor con pétalos y que se puede expresar como una simple ecuación polar,

r()φ φ )=a#⁡ ⁡ ()kφ φ +γ γ 0){displaystyle r(varphi)=acos left(kvarphi +gamma _{0}right)}

para cualquier constante γ₀ (incluido 0). Si k es un número entero, estas ecuaciones producirán una rosa de pétalos k si k es impar, o un 2k-rosa de pétalos si k es par. Si k es racional, pero no un número entero, se puede formar una forma de rosa pero con pétalos superpuestos. Tenga en cuenta que estas ecuaciones nunca definen una rosa con 2, 6, 10, 14, etc. pétalos. La variable a representa directamente la longitud o amplitud de los pétalos de la rosa, mientras que k se relaciona con su frecuencia espacial. La constante γ₀ puede considerarse como un ángulo de fase.

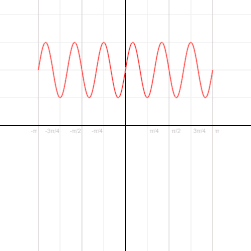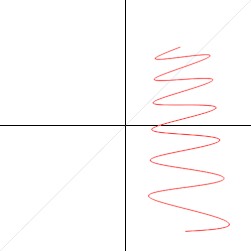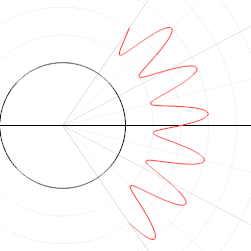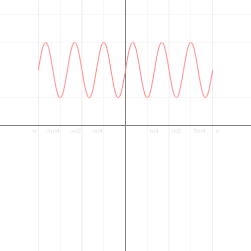
Espiral de Arquímedes

Un brazo de una espiral arquímica con ecuación r()φ) φ / 2π para 0 φ 6πpi

La espiral de Arquímedes es una espiral descubierta por Arquímedes que también se puede expresar como una ecuación polar simple. está representado por la ecuación

r()φ φ )=a+bφ φ .{displaystyle r(varphi)=a+bvarphi.}

Elipse, mostrando recto semi-latus

Secciones cónicas

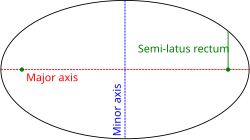
Una sección cónica con un foco en el polo y el otro en algún lugar del rayo 0° (de modo que el eje mayor de la cónica se encuentre a lo largo del eje polar) viene dada por:

r=l l 1− − e#⁡ ⁡ φ φ {displaystyle r={ell over {1-ecos varphi }

l l {displaystyle ell }

l l {displaystyle ell }

Intersección de dos curvas polares

Los gráficos de dos funciones polares r=f()Silencio Silencio ){displaystyle r=f(theta)} y r=g()Silencio Silencio ){displaystyle r=g(theta)} tienen posibles intersecciones de tres tipos:

1. En el origen, si las ecuaciones f()Silencio Silencio )=0{displaystyle f(theta)=0} y g()Silencio Silencio )=0{displaystyle g(theta)=0} tienen al menos una solución cada uno.
2. Todos los puntos [g()Silencio Silencio i),Silencio Silencio i]{displaystyle [g(theta _{i}),theta _{i}} Donde Silencio Silencio i{displaystyle theta _{i} son soluciones a la ecuación f()Silencio Silencio +2kπ π )=g()Silencio Silencio ){displaystyle f(theta +2kpi)=g(theta)} Donde k{displaystyle k} es un entero.
3. Todos los puntos [g()Silencio Silencio i),Silencio Silencio i]{displaystyle [g(theta _{i}),theta _{i}} Donde Silencio Silencio i{displaystyle theta _{i} son soluciones a la ecuación f()Silencio Silencio +()2k+1)π π )=− − g()Silencio Silencio ){displaystyle f(theta +(2k+1)pi)=-g(theta)} Donde k{displaystyle k} es un entero.

Cálculo

El cálculo se puede aplicar a ecuaciones expresadas en coordenadas polares.

La coordenada angular φ se expresa en radianes a lo largo de esta sección, que es la opción convencional al hacer cálculos.

Cálculo diferencial

Utilizando x = r cos φ y y = r sin φ, se puede derivar una relación entre derivadas en coordenadas cartesianas y polares. Para una función dada, u(x,y), se sigue que (al calcular sus derivadas totales) o

rdudr=r∂ ∂ u∂ ∂ x#⁡ ⁡ φ φ +r∂ ∂ u∂ ∂ Sí.pecado⁡ ⁡ φ φ =x∂ ∂ u∂ ∂ x+Sí.∂ ∂ u∂ ∂ Sí.,dudφ φ =− − ∂ ∂ u∂ ∂ xrpecado⁡ ⁡ φ φ +∂ ∂ u∂ ∂ Sí.r#⁡ ⁡ φ φ =− − Sí.∂ ∂ u∂ ∂ x+x∂ ∂ u∂ ∂ Sí..{fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}

Por lo tanto, tenemos las siguientes fórmulas:

rddr=x∂ ∂ ∂ ∂ x+Sí.∂ ∂ ∂ ∂ Sí.ddφ φ =− − Sí.∂ ∂ ∂ ∂ x+x∂ ∂ ∂ ∂ Sí..{displaystyle {begin{aligned}r{frac} {dr} {dr} {fnMicroc} {partial }{partial ¿Qué? ♪♪♪ {partial }{partial x}+x{frac {partial }{partial y}}end{aligned}}}}

Usando la transformación de coordenadas inversas, se puede derivar una relación recíproca análoga entre las derivadas. Dada una función u(r,φ), se sigue que

dudx=∂ ∂ u∂ ∂ r∂ ∂ r∂ ∂ x+∂ ∂ u∂ ∂ φ φ ∂ ∂ φ φ ∂ ∂ x,dudSí.=∂ ∂ u∂ ∂ r∂ ∂ r∂ ∂ Sí.+∂ ∂ u∂ ∂ φ φ ∂ ∂ φ φ ∂ ∂ Sí.,{displaystyle {begin{aligned}{frac {du}{dx} {frac {partial u}{partial r}}{frac {partial r}{partial x}}+{frac {partial u}{partial varphi}{bi}}}{f}}}}}} {f} {f}}f}}}}}}}}f}}}f}f}f}f}}f}f}f}f}}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f} {f}f}f}f}f}f}}f}f}f}f}f}f}f}f}f}f}} {fnMicroc {cHFF}{partial x}},[2pt]{frac {}{y}} {f} {f}} {f}} {fnMicroc}}} {fnMicroc} {f}} {fnf}}}} {fnMicroc} {f}}}} {f}}}}}}} {\fn\\fnMicrocfnfnMicroc}fnfnfnfnfnfnfnKfnfnfn\fnfnfnfn\fnMicrocfnKfnMicroc}}}}}\\fn\\fnKfnfnfnK\\fnMicroc\fnfnMicrocfnMicroc}}}\fn {partial u}{partial r}{partial r}{partial y}}+{frac {partial u}{partial varphi }{frac {partial varphi } {partial y}}end{aligned}}

dudx=∂ ∂ u∂ ∂ rxx2+Sí.2− − ∂ ∂ u∂ ∂ φ φ Sí.x2+Sí.2=#⁡ ⁡ φ φ ∂ ∂ u∂ ∂ r− − 1rpecado⁡ ⁡ φ φ ∂ ∂ u∂ ∂ φ φ ,dudSí.=∂ ∂ u∂ ∂ rSí.x2+Sí.2+∂ ∂ u∂ ∂ φ φ xx2+Sí.2=pecado⁡ ⁡ φ φ ∂ ∂ u∂ ∂ r+1r#⁡ ⁡ φ φ ∂ ∂ u∂ ∂ φ φ .{displaystyle {begin{aligned}{}{dx} {begin{aligned}{frac {f}{f} {f} {f} {f}}}} {fn}}} {fnf}} {fnf}f}fnfnKf} {f}f}}}}}}}}}}}}}}}}}}}}}}b9b9}}}}}}}}}}}}}}} {b}}}}}}}}}}}}}}}}}}}}}} {b} {b}}}}}}}} {b9b}}}}}}}}}}}}}}}}}}}}}}}}b}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m}}}}}}}}}} {fnMicroc {x} {fnMicrosoft} {fnMicrosoft} {fnK}} {fn}} {fn}} {fn} {fnK}}} {fn}} {fn} {fnK}} {f}}} {fnK}}}} {f}f}f}f}f}f}f}f}f}f}fn}f}f}f}f}fn}f}fnfnfnfnfnfnf}fnf}fnfnfnfnKfnfnfnfnfnfnfnfnfnfnfnfnfnKfn}fnfnfnfn}fnfnh}fnfn {fnMicroc} {partial u}{partial varphi } {frac {y}{2}+y^{2}}\[2pt] Con=cos varphi {frac {partial u}{partial r}-{frac {1}{r}sin varphi {frac {partial u}{partial varphi }\[2pt]{frac {du}{y} {} {frac} {frac} {f}{f}} {f}} {f} {f} {f}fnKf}f}f}f}f}f}f}fnKf}fnfnKfnfnKfnKfnfnKfnfnKfnfnKfnfnfnf}fnf}fnfnKfnKfnKfnfnfnfnfnfnfnKfnfnKfnfnKfnfnfnfnfnfnKfnfnf}fn {partial u}{partial {fnMicroc {y} {fnMicrosoft} {fnMicroc} {fnMicroc} {fn} {fn}} {fn}} {fn} {fn}} {fn}} {fn}} {fn}} {fn}}} {fn}}} {f}f}f}f}f}f}f}f}f}fn}f}fn}f}f}fn}f}fnfnfn}fnfn}f}fnfnfn}fnfn}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfn}fnfn}fnfn}fnfn}}}}fn {fnMicroc} {partial u}{partial varphi }{frac {x}{2}+y^{2}}[2pt] Con=sin varphi {frac {partial u}{partial}{2pt] r}+{frac {1} {cos varphi {frac {partial u}{partial varphi }}}end{aligned}}}}}

Por lo tanto, tenemos las siguientes fórmulas:

ddx=#⁡ ⁡ φ φ ∂ ∂ ∂ ∂ r− − 1rpecado⁡ ⁡ φ φ ∂ ∂ ∂ ∂ φ φ ddSí.=pecado⁡ ⁡ φ φ ∂ ∂ ∂ ∂ r+1r#⁡ ⁡ φ φ ∂ ∂ ∂ ∂ φ φ .{displaystyle {begin{aligned}{frac} {fnK} {fnK} {fnK}} {fn}}} {fn}} {fn}} {c}}}}}}}}} {cc}} {fn}}}}}} {cc}}}}ccccccccc}}}}} {c}}}}}}}}}ccc}}}}ccccccccccccccccccccccc}}}}}}}}}}}ccccccccccccccccccccccccccccccccc}}}}}}}}}}}} }{partial. {1}{}sin varphi {frac {partial }{partial varphi }\[2pt]{frac {d} {d} {d} {} {fn} {fn} {fn} {fn}} {fn} {f}}}} {fn} {fn} {f}}}}}}\fn}}\\\\\fn}fn}fn}fn}fn}fn}fn}fn}fn}fn}\fn}fn}\\\\\\\\\\\\fn}\fn}\\fn}\\\\\\\\\\\\\\\\\\\\fn}\fn} varphi {frac {partial }{partial r}+{frac {1}}cos varphi {frac {partial }{partial varphi }}}end{aligned}}}}

Para encontrar la pendiente cartesiana de la recta tangente a una curva polar r(φ) en cualquier punto dado, primero se expresa la curva como un sistema de ecuaciones paramétricas.

x=r()φ φ )#⁡ ⁡ φ φ Sí.=r()φ φ )pecado⁡ ⁡ φ φ {displaystyle {begin{aligned}x limit=r(varphi)cos varphi \y paciente=r(varphi)sin varphi end{aligned}}

Derivando ambas ecuaciones con respecto a φ se obtiene

dxdφ φ =r.()φ φ )#⁡ ⁡ φ φ − − r()φ φ )pecado⁡ ⁡ φ φ dSí.dφ φ =r.()φ φ )pecado⁡ ⁡ φ φ +r()φ φ )#⁡ ⁡ φ φ .{displaystyle {begin{aligned}{frac {dx}{dvarphi } {=r'(varphi)cos varphi -r(varphi)sin varphi \[2pt]{frac {}{dvarphi }} {varphi}varphi]sin varphi +r {f}{varphialf}}}}}}}} {f}}}}}}}}} {f} {f} {f}f}fnMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMientras, miren, miren, miren, miren, miren, miren, miren, miren, miren, miren, miren, miren, miren, miren, miren, miren, miren, miren, miren, mi

Dividiendo la segunda ecuación por la primera se obtiene la pendiente cartesiana de la recta tangente a la curva en el punto (r(φ), φ):

dSí.dx=r.()φ φ )pecado⁡ ⁡ φ φ +r()φ φ )#⁡ ⁡ φ φ r.()φ φ )#⁡ ⁡ φ φ − − r()φ φ )pecado⁡ ⁡ φ φ .{displaystyle {frac {y}={frac {r'(varphi)sin varphi +r(varphi)cos varphi }{r'(varphi)cos varphi -r(varphi)sin varphi }}

Para otras fórmulas útiles, como divergencia, gradiente y laplaciana en coordenadas polares, consulte coordenadas curvilíneas.

Cálculo integral (longitud de arco)

La longitud del arco (longitud de un segmento de línea) definida por una función polar se encuentra mediante la integración sobre la curva r(φ). Sea L esta longitud a lo largo de la curva que comienza desde los puntos A hasta el punto B, donde estos puntos corresponden a φ = a y φ = b tales que 0 < b − a < 2π. La longitud de L viene dada por la siguiente integral

L=∫ ∫ ab[r()φ φ )]2+[dr()φ φ )dφ φ ]2dφ φ {displaystyle L=int _{a}{b}{sqrt {left[r(varphi)right]^{2}+left[{tfrac {dr(varphi)}{dvarphi }right]} {2}dvarphi }}}}}}dvarphi }}} {} {dvarphi}}}}}}}}}}}}}}}} {dddvarphi}}}}}}}}}}}}}}}}}} {ddvarphi}}}}}}}}}}}}}}}}}}}}}}}}}}}} {ddvarphi}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {h}}}}}}}} {h}}}}}}}}} {h}}}}}}}}}}}} {

Cálculo integral (área)

La región de integración R está atado por la curva r()φ) y los rayos φ = a y φ = b.

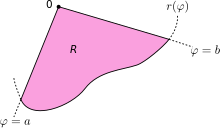
Sea R la región encerrada por una curva r(φ) y los rayos φ = a y φ = b, donde 0 < b − a ≤ 2π. Entonces, el área de R es

12∫ ∫ ab[r()φ φ )]2dφ φ .{displaystyle {frac {2}int_{a}b}left[r(varphi)right]^{2},dvarphi.}

La región R es aproximado por n sectores (aquí, n = 5).

Un plano, que computa mecánicamente integrales polares

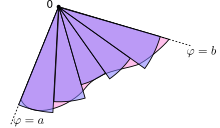
Este resultado se puede encontrar de la siguiente manera. Primero, el intervalo [a, b] se divide en n subintervalos, donde n es un entero positivo. Por lo tanto, Δφ, la medida del ángulo de cada subintervalo, es igual a b − a (la medida del ángulo total del intervalo), dividida por n, el número de subintervalos. Para cada subintervalo i = 1, 2,..., n, sea φ_i sea el punto medio del subintervalo, y construya un sector con el centro en el polo, radio r(φ_i ), ángulo central Δφ y longitud de arco r(φ_i)Δφ. El área de cada sector construido es por lo tanto igual a

[r()φ φ i)]2π π ⋅ ⋅ Δ Δ φ φ 2π π =12[r()φ φ i)]2Δ Δ φ φ .{displaystyle left[r(varphi _{i})right]^{2}pi cdot {frac {Delta varphi }{2pi Delta varphi.

.. i=1n12r()φ φ i)2Δ Δ φ φ .{displaystyle sum Delta varphi.

A medida que aumenta el número de subintervalos n, mejora la aproximación del área. Tomando n → ∞, la suma se convierte en la suma de Riemann para la integral anterior.

Un dispositivo mecánico que calcula integrales de área es el planímetro, que mide el área de figuras planas trazándolas: esto replica la integración en coordenadas polares agregando una articulación para que el enlace de 2 elementos efectúe el teorema de Green., convirtiendo la integral polar cuadrática en una integral lineal.

Generalización

Usando coordenadas cartesianas, un elemento de área infinitesimal se puede calcular como dA = dx dy. La regla de sustitución para integrales múltiples establece que, al usar otras coordenadas, se debe considerar el determinante jacobiano de la fórmula de conversión de coordenadas:

J=Det∂ ∂ ()x,Sí.)∂ ∂ ()r,φ φ )=Silencio∂ ∂ x∂ ∂ r∂ ∂ x∂ ∂ φ φ ∂ ∂ Sí.∂ ∂ r∂ ∂ Sí.∂ ∂ φ φ Silencio=Silencio#⁡ ⁡ φ φ − − rpecado⁡ ⁡ φ φ pecado⁡ ⁡ φ φ r#⁡ ⁡ φ φ Silencio=r#2⁡ ⁡ φ φ +rpecado2⁡ ⁡ φ φ =r.{displaystyle J=det {frac {partial (x,y)}{partial (r,varphi)}={begin{vmatrix}{frac {partial x}{partial r} {frac {partial x}{partialvarphi}}}}[2pt]{frac} {f} {f} {f}}f}}}}}f}f}f}f}f}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f }end{vmatrix}={begin{vmatrix}cos varphi &-rsin varphi \sin varphi &rcos varphi end{vmatrix}=rcos ^{2}varphi +rsin ^{2}varphi =r.}

Por lo tanto, un elemento de área en coordenadas polares se puede escribir como

dA=dxdSí.=Jdrdφ φ =rdrdφ φ .{fnMicrosoft Sans Serif}

Ahora, una función, que se da en coordenadas polares, se puede integrar de la siguiente manera:

∫ ∫ Rf()x,Sí.)dA=∫ ∫ ab∫ ∫ 0r()φ φ )f()r,φ φ )rdrdφ φ .{displaystyle iint _{R}f(x,y),dA=int _{a}^{b}int _{0}^{r(varphi)}f(r,varphi),r,dr,dvarphi.}

Aquí, R es la misma región que arriba, es decir, la región encerrada por una curva r(φ) y los rayos φ = a y φ = b. La fórmula para el área de R se recupera tomando f igual a 1.

Un gráfico de f()x)=e− − x2{displaystyle f(x)=e^{-x^{2}} y el área entre la función y la x{displaystyle x}-eje, que es igual a π π {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\\\\\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn\\\\\\\\\\\\\\\\\\\\\\\\\\\fn }.

Una aplicación más sorprendente de este resultado produce la integral de Gauss:

∫ ∫ − − JUEGO JUEGO JUEGO JUEGO e− − x2dx=π π .{displaystyle int _{-infty }e^{-x^{2},dx={sqrt {pi}}

Cálculo vectorial

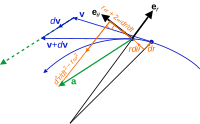
El cálculo vectorial también se puede aplicar a las coordenadas polares. Para un movimiento planificador, deja r{displaystyle mathbf {r} ser el vector de posición ()r Porque...φ), r pecado(φ), con r y φ dependiendo del tiempo t.

Definimos los vectores unitarios

r^ ^ =()#⁡ ⁡ ()φ φ ),pecado⁡ ⁡ ()φ φ )){displaystyle {hat {mathbf {r}}=(cos(varphi),sin(varphi)}

r{displaystyle mathbf {r}

φ φ ^ ^ =()− − pecado⁡ ⁡ ()φ φ ),#⁡ ⁡ ()φ φ ))=k^ ^ × × r^ ^ ,{displaystyle {hat {boldsymbol {varphi }}=(sin(varphi),cos(varphi)={hat {mathbf {k} }times {hat {mathbf {r} }

k^ ^ {displaystyle {hat {mathbf} }

Entonces

r=()x,Sí.)=r()#⁡ ⁡ φ φ ,pecado⁡ ⁡ φ φ )=rr^ ^ ,rÍ Í =()xÍ Í ,Sí.Í Í )=rÍ Í ()#⁡ ⁡ φ φ ,pecado⁡ ⁡ φ φ )+rφ φ Í Í ()− − pecado⁡ ⁡ φ φ ,#⁡ ⁡ φ φ )=rÍ Í r^ ^ +rφ φ Í Í φ φ ^ ^ ,r.. =()x.. ,Sí... )=r.. ()#⁡ ⁡ φ φ ,pecado⁡ ⁡ φ φ )+2rÍ Í φ φ Í Í ()− − pecado⁡ ⁡ φ φ ,#⁡ ⁡ φ φ )+rφ φ .. ()− − pecado⁡ ⁡ φ φ ,#⁡ ⁡ φ φ )− − rφ φ Í Í 2()#⁡ ⁡ φ φ ,pecado⁡ ⁡ φ φ )=()r.. − − rφ φ Í Í 2)r^ ^ +()rφ φ .. +2rÍ Í φ φ Í Í )φ φ ^ ^ =()r.. − − rφ φ Í Í 2)r^ ^ +1rddt()r2φ φ Í Í )φ φ ^ ^ .{fnMicrosoft Sans Serif} {f} {f} {f} {f} {f}f} {f}f} {f}f} {f}f}f} {f}f}f}f} {f}f}f}f}cH00}f}f}f} {f}f}f} ### {f} {f} {f} {f}f} {f}f} {f} {f} {f}f}f} {f}f} {f}f}f}f}f} {f}f} {f}cH00}f}f}f}f}f}f}f}f}f}f}f}f}f}f} {f}f}f}f}f} {cH00}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f} }+left(r{ddot [varphi }}+2{dot {dot { dot {varphi }right){hat {boldsymbol {varphi {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {}};{frac {d}}left(r^{2}{dot {varphi }}right){hat {boldsymbol {varphi }}}end{aligned}}}}}}}}}}}}}}}} {fnf}} {f}}f}}}}}}}}}}}}}f}}\f} {f}f}}f}f}}f}f}}f}f}f} {f}f}f}f}}f}}}}}f}}\f}f}}}}f}}}fnf}}fnf}}fnfnf}f}}}}}}}fnf}}fnf}fnfn\\f}}}}}}}}}

Esta ecuación se puede obtener tomando derivadas de la función y derivadas de los vectores de base unitaria.

Para una curva en 2D con el parámetro es Silencio Silencio {displaystyle theta } la ecuación anterior simplifica:

r→ → =r()Silencio Silencio )e^ ^ rdr→ → dSilencio Silencio =drdSilencio Silencio e^ ^ r+re^ ^ Silencio Silencio d2r→ → dSilencio Silencio 2=()d2rdSilencio Silencio 2− − r)e^ ^ r+drdSilencio Silencio e^ ^ Silencio Silencio {displaystyle {begin{aligned}{vec {r} {theta){hat {fnMicroc} {d {fnK} {d} {d}theta ♪♪♪♪♪♪frac {dtheta }{hat {fnh} {fnh} {fnh} {fnh}} {fnh} {fnh}} {fnh}}fn}fn}fn}fn} {fnfn}}\fnh}f}}\fnh}fnf}fn}}}}}}\\\\\fn}}}}}}}}}}}\\\\\\\fn}}}}}\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {e}_{theta ♫{frac {fnK} {fnK}} {fnK}} {fnK}} {fnMic {f} {f}} {fn}} {fnK}} {fnK}} {fnK}}} {f}} {f}}}}} {fnKf}}} {f}}}}}}}}}}}} {f}f}}}}}}f}}}}}}}}}} {f} {f}} {f}f}}}}}}}}}} {f}}}}} {f} {f}}}} {f} {f}}}}} {f}}}} {f}}}} {f}}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {fnMicroc} {dr}{dtheta {fnK} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fn}} {f}}} {fn} {fn}} {fn}}}} {fn}} {f} {fnf}}}} {fnf}} {f}}} {f} {f} {f}} {f}}}}}}} {f} {f} {f}}}}} {f}}}}}}}}}}} {f} {f} {f} {f}}}}} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}} {f} {f} {f} {f} {f} {f} {f} {f} {f}}} {f}} }end{aligned}}

Términos centrífugos y de Coriolis

Cargo r, siempre apunta radialmente desde el origen.

Velocity vector vSiempre tangente al camino del movimiento.

vector de aceleración a, no paralelo al movimiento radial, sino compensado por las aceleraciones angular y coriolis, ni tangente al camino, sino compensado por las aceleraciones centrípetas y radiales.

vectores Kinematic en coordenadas polares de avión. Observe que la configuración no está restringida al espacio 2d, sino un plano en cualquier dimensión superior.

El término rφ φ Í Í 2{displaystyle r{dot {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {\\fnMicrosoft {\\\fnMicrosoft\\\\\\\fnMicrosoft\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ } {2} a veces se conoce como aceleración centrípeta, y el término 2rÍ Í φ φ Í Í {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft} {f}}}} {fnMicrosoft} {fnMicrosoft}}}} {fnMicrosoft}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}f}f}}}}}}}}}}}}}}}}}} { } como Aceleración de Coriolis. Por ejemplo, vea Shankar.

Nota: estos términos, que aparecen cuando la aceleración se expresa en coordenadas polares, son una consecuencia matemática de la diferenciación; aparecen siempre que se utilizan coordenadas polares. En la dinámica de partículas planas, estas aceleraciones aparecen cuando se establece la segunda ley del movimiento de Newton en un marco de referencia giratorio. Aquí, estos términos adicionales a menudo se denominan fuerzas ficticias; ficticios porque son simplemente el resultado de un cambio en el marco de coordenadas. Eso no significa que no existan, sino que solo existen en el marco giratorio.

Marco de referencia inercial S y marco de co-rotación instantánea no inercial S′. El marco co-rotante gira a velocidad angular Ω igual a la tasa de rotación de la partícula sobre el origen de la S′ en el momento particular t. La partícula se encuentra en posición vectorial r()t) y vectores de unidad se muestran en la dirección radial a la partícula desde el origen, y también en la dirección del ángulo creciente φ normal a la dirección radial. Estos vectores de unidad no necesitan estar relacionados con el tangente y normal al camino. Además, la distancia radial r no debe estar relacionado con el radio de curvatura del camino.

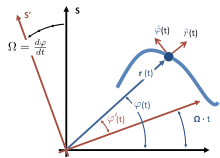
Marco co-rotatorio

Para una partícula en movimiento plano, un enfoque para otorgar significado físico a estos términos se basa en el concepto de un marco de referencia co-rotatorio instantáneo. Para definir un marco co-rotante, primero se selecciona un origen desde el cual se define la distancia r(t) a la partícula. Se establece un eje de rotación que es perpendicular al plano de movimiento de la partícula y que pasa por este origen. Luego, en el momento seleccionado t, la velocidad de rotación del marco corrotante Ω se hace coincidir con la velocidad de rotación de la partícula sobre este eje, dφ/ dt. A continuación, los términos de la aceleración en el marco inercial se relacionan con los del marco co-rotatorio. Sea la ubicación de la partícula en el marco inercial (r(t), φ(t)), y en el marco de co-rotación sea (r′(t), φ′(t)). Debido a que el marco corrotante gira a la misma velocidad que la partícula, dφ′/dt = 0. La fuerza centrífuga ficticia en el marco corrotante es mrΩ², radialmente hacia afuera. La velocidad de la partícula en el marco de co-rotación también es radialmente hacia afuera, porque dφ′/dt = 0. La fuerza de Coriolis ficticia por lo tanto tiene un valor −2m(dr/dt)Ω, apuntando en la dirección de aumento de φ solamente. Así, usando estas fuerzas en la segunda ley de Newton encontramos:

F+Fcf+FCor=mr.. ,{displaystyle {boldsymbol {F}+{boldsymbol {F}_{text{cf}+{boldsymbol {F}_{text{Cor}=m{ddot {fnK}}

Fr+mrΩ Ω 2=mr.. Fφ φ − − 2mrÍ Í Ω Ω =mrφ φ .. ,{displaystyle {begin{aligned}F_{r}+mrOmega ^{2} {r}fn}\fn\\fnMicrosoft Sans Serif} 2m{dot {r} Omega.

Fr=mr.. − − mrφ φ Í Í 2Fφ φ =mrφ φ .. +2mrÍ Í φ φ Í Í .{displaystyle {begin{aligned}F_{r} {}-mr{dot {fnh}. }=mr{ddot {varphi }+2m{dot { dot { dot {varphi }.end{aligned}}}

Esta comparación, más el reconocimiento de que por la definición del marco de co-rotación en el tiempo t tiene una tasa de rotación Ω = dφ/dt , muestra que podemos interpretar los términos de la aceleración (multiplicada por la masa de la partícula) que se encuentran en el marco inercial como el negativo de las fuerzas centrífugas y de Coriolis que se verían en el instante, no inercial marco co-rotatorio.

Para el movimiento general de una partícula (a diferencia del movimiento circular simple), las fuerzas centrífugas y de Coriolis en el marco de referencia de una partícula comúnmente se refieren al círculo osculador instantáneo de su movimiento, no a un centro fijo de coordenadas polares. Para más detalles, véase fuerza centrípeta.

Geometría diferencial

En la terminología moderna de geometría diferencial, las coordenadas polares proporcionan gráficos de coordenadas para la variedad diferenciable R² {(0,0)}, el plano menos el origen. En estas coordenadas, el tensor métrico euclidiano viene dado por

ds2=dr2+r2dSilencio Silencio 2.{displaystyle ds^{2}=dr^{2}+r^{2}dtheta ^{2}

er=∂ ∂ ∂ ∂ r,eSilencio Silencio =1r∂ ∂ ∂ ∂ Silencio Silencio ,{displaystyle e_{r}={frac {partial }{partial r}quad e_{theta {fnMicroc {} {fnMicroc {partial}{partial theta}}}}

er=dr,eSilencio Silencio =rdSilencio Silencio .{displaystyle e^{r}=dr,quad e^{theta - Sí.

⋅ ⋅ ij=()0− − dSilencio Silencio dSilencio Silencio 0){displaystyle {omega }_{j}={begin{pmatrix}0 ventaja-dtheta {fnK}

Extensiones en 3D

El sistema de coordenadas polares se extiende a tres dimensiones con dos sistemas de coordenadas diferentes, el sistema de coordenadas cilíndrico y esférico.

Aplicaciones

Las coordenadas polares son bidimensionales y, por lo tanto, solo se pueden usar cuando las posiciones de los puntos se encuentran en un único plano bidimensional. Son más apropiados en cualquier contexto donde el fenómeno que se está considerando está ligado inherentemente a la dirección y la longitud desde un punto central. Por ejemplo, los ejemplos anteriores muestran cómo las ecuaciones polares elementales son suficientes para definir curvas, como la espiral de Arquímedes, cuya ecuación en el sistema de coordenadas cartesianas sería mucho más compleja. Además, muchos sistemas físicos, como los relacionados con cuerpos que se mueven alrededor de un punto central o con fenómenos que se originan en un punto central, son más simples e intuitivos de modelar usando coordenadas polares. La motivación inicial para la introducción del sistema polar fue el estudio del movimiento circular y orbital.

Posición y navegación

Las coordenadas polares se utilizan a menudo en la navegación, ya que el destino o la dirección de viaje se pueden dar como un ángulo y una distancia desde el objeto que se está considerando. Por ejemplo, los aviones utilizan una versión ligeramente modificada de las coordenadas polares para la navegación. En este sistema, el que generalmente se usa para cualquier tipo de navegación, el rayo 0° generalmente se denomina rumbo 360, y los ángulos continúan en el sentido de las agujas del reloj, en lugar de en el sentido contrario a las agujas del reloj, como en el sistema matemático. El rumbo 360 corresponde al norte magnético, mientras que los rumbos 90, 180 y 270 corresponden al este, sur y oeste magnéticos, respectivamente. Por lo tanto, un avión que viaja 5 millas náuticas hacia el este viajará 5 unidades en el rumbo 90 (léase cero-nueve-cero por el control de tráfico aéreo).

Modelado

Los sistemas que muestran simetría radial proporcionan configuraciones naturales para el sistema de coordenadas polares, con el punto central actuando como el polo. Un buen ejemplo de este uso es la ecuación de flujo de agua subterránea cuando se aplica a pozos radialmente simétricos. Los sistemas con una fuerza radial también son buenos candidatos para el uso del sistema de coordenadas polares. Estos sistemas incluyen campos gravitatorios, que obedecen la ley del inverso del cuadrado, así como sistemas con fuentes puntuales, como antenas de radio.

Los sistemas radialmente asimétricos también se pueden modelar con coordenadas polares. Por ejemplo, el patrón de captación de un micrófono ilustra su respuesta proporcional a un sonido entrante desde una dirección determinada, y estos patrones se pueden representar como curvas polares. La curva de un micrófono cardioide estándar, el micrófono unidireccional más común, se puede representar como r = 0,5 + 0,5sin(ϕ) a su frecuencia de diseño de destino. El patrón cambia hacia la omnidireccionalidad en frecuencias más bajas.