Sistema de coordenadas cilíndricas

Un sistema de coordenadas cilíndricas con origen O, eje polar A, y eje longitudinal L. El punto es el punto con distancia radial *** = 4, coordinación angular φ = 130°, y altura z = 4.

Un sistema de coordenadas cilíndricas es un sistema de coordenadas tridimensional que especifica posiciones de puntos por la distancia desde un eje de referencia elegido (eje L en la imagen opuesta), el dirección desde el eje relativo a una dirección de referencia elegida (eje A), y la distancia desde un plano de referencia elegido perpendicular al eje (plano que contiene la sección morada). La última distancia se da como un número positivo o negativo según el lado del plano de referencia que enfrenta el punto.

El origen del sistema es el punto donde las tres coordenadas se pueden dar como cero. Esta es la intersección entre el plano de referencia y el eje. El eje se denomina eje cilíndrico o longitudinal, para diferenciarlo del eje polar, que es el rayo que se encuentra en el plano de referencia., comenzando en el origen y apuntando en la dirección de referencia. Otras direcciones perpendiculares al eje longitudinal se denominan líneas radiales.

La distancia desde el eje puede llamarse distancia radial o radio, mientras que la coordenada angular a veces se denomina posición angular o como el azimut. El radio y el acimut se denominan conjuntamente coordenadas polares, ya que corresponden a un sistema de coordenadas polares bidimensionales en el plano que pasa por el punto, paralelo al plano de referencia. La tercera coordenada puede denominarse altura o altitud (si el plano de referencia se considera horizontal), posición longitudinal o posición axial .

Las coordenadas cilíndricas son útiles en relación con objetos y fenómenos que tienen cierta simetría rotacional sobre el eje longitudinal, como el flujo de agua en una tubería recta con sección transversal redonda, la distribución de calor en un cilindro de metal, los campos electromagnéticos producidos por un corriente en un cable largo y recto, discos de acreción en astronomía, etc.

A veces se les llama "coordenadas polares cilíndricas" y "coordenadas cilíndricas polares", y a veces se utilizan para especificar la posición de las estrellas en una galaxia ("coordenadas polares cilíndricas galactocéntricas").

Definición

Las tres coordenadas (ρ, φ, z) de un punto P se definen como:

• El distancia axial o distancia radial *** es la distancia euroclidiana de la z-eje al punto P.
• El azimuth φ es el ángulo entre la dirección de referencia en el plano elegido y la línea desde el origen a la proyección de P en el avión.
• El coordinación axial o altura z es la distancia firmada desde el plano elegido hasta el punto P.

Coordenadas cilíndricas únicas

Como en coordenadas polares, el mismo punto con coordenadas cilíndricas (ρ, φ, z) tiene infinitas coordenadas equivalentes, a saber, (ρ, φ ± n×360°, z) y (−ρ, φ ± (2n + 1)×180°, z), donde n es cualquier entero. Además, si el radio ρ es cero, el acimut es arbitrario.

En situaciones en las que alguien quiere un conjunto único de coordenadas para cada punto, se puede restringir el radio para que no sea negativo (ρ ≥ 0) y el acimut φ para estar en un intervalo específico que abarca 360°, como [− 180°,+180°] o [0,360°].

Convenios

La notación para coordenadas cilíndricas no es uniforme. La norma ISO 31-11 recomienda (ρ, φ, z), donde ρ es la coordenada radial, φ el acimut y z la altura. Sin embargo, el radio también se suele indicar r o s, el acimut por θ o t, y la tercera coordenada por h o (si el eje cilíndrico se considera horizontal) x, o cualquier letra específica del contexto.

Las superficies de coordenadas de las coordenadas cilíndricas ()***, φ, z). El cilindro rojo muestra los puntos con *** = 2, el plano azul muestra los puntos con z = 1, y el medio plano amarillo muestra los puntos con φ = 60°. El z-eje es vertical y el x-eje se destaca en verde. Las tres superficies se intersectan en el punto P con esas coordenadas (shown como esfera negra); las coordenadas cartesianas de P son aproximadamente (1.0, 1,732, 1.0).

Superficies de coordenadas cilíndricas. Los tres componentes ortogonales, *** (verde) φ (red), and z (azul), cada aumento a un ritmo constante. El punto está en la intersección entre las tres superficies de colores.

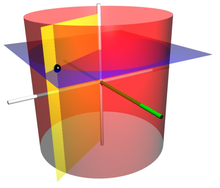
En situaciones concretas y en muchas ilustraciones matemáticas, una coordenada angular positiva se mide en sentido antihorario visto desde cualquier punto con altura positiva.

Conversiones del sistema de coordenadas

El sistema de coordenadas cilíndricas es uno de los muchos sistemas de coordenadas tridimensionales. Las siguientes fórmulas se pueden utilizar para convertir entre ellos.

Coordenadas cartesianas

Para la conversión entre coordenadas cilíndricas y cartesianas, es conveniente asumir que el plano de referencia de las primeras es el cartesiano xy-plano (con ecuación z = 0), y el eje cilíndrico es el cartesiano z-eje. Entonces la coordenada z es la misma en ambos sistemas, y la correspondencia entre (ρ, φ, z) y cartesiano (x, y, z) son los mismos que para las coordenadas polares, es decir

x=*** *** #⁡ ⁡ φ φ Sí.=*** *** pecado⁡ ⁡ φ φ z=z{displaystyle {begin{aligned}x limit=rho varphi \y tro=rho sin varphi \z limit=zend{aligned}}

Mediante el uso de la función arctangente que devuelve también un ángulo en el rango [-π/2, +π/2] = [90 - 90°, +90°], uno también puede calcular φ φ {displaystyle varphi } sin computación *** *** {displaystyle rho } primero

0\arctan left({frac {y}{x}}right)+pi &{mbox{if }}x<0{text{ and }}ygeq 0\arctan left({frac {y}{x}}right)-pi &{mbox{if }}x<0{text{ and }}yφ φ ={}indeterminadosix=0ySí.=0π π 2Sí.SilencioSí.Silenciosix=0ySí.ل ل 0arctan⁡ ⁡ ()Sí.x)six■0arctan⁡ ⁡ ()Sí.x)+π π six.0ySí.≥ ≥ 0arctan⁡ ⁡ ()Sí.x)− − π π six.0ySí..0{displaystyle {begin{aligned}varphi > {begin{cases}{text{indeterminate}} {text{if{if} }x=0{text{ y }y=0\{frac {pi {fnK} {fnK} {fnK} {fnK}} {fnK}} {fnK}} {f}}}}} {f}}} {fn}}}}} {fn}}} {f}}} {f}}}} {fnfnf}}}}} {f} {f}f}}}}}}f}f}f}fn}fnf}f}f}f}fnf}fnfnfnfnfnfnf}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfn}fnfnfnfnfnfnfn}fnfn }x=0{text{ and }}yneq 0\\\arctan left({frac {y}{x}right) ################################################################################################################################################################################################################################################################

0\arctan left({frac {y}{x}}right)+pi &{mbox{if }}x<0{text{ and }}ygeq 0\arctan left({frac {y}{x}}right)-pi &{mbox{if }}x<0{text{ and }}y

Muchos lenguajes de programación modernos proporcionan una función que calculará el azimut correcto φ, en el rango (−π, π), dados x e y, sin necesidad de realizar un análisis de casos como el anterior. Por ejemplo, esta función es llamada por atan2(y, x) en el lenguaje de programación C, y (atan y x) en Common Lisp.

Coordenadas esféricas

Coordenadas esféricas (radio r, elevación o inclinación θ, acimut φ), puede convertirse en coordenadas cilíndricas mediante:

Silencio es la elevación:	Silencio es la inclinación:
*** *** =r#⁡ ⁡ Silencio Silencio φ φ =φ φ z=rpecado⁡ ⁡ Silencio Silencio {displaystyle {begin{aligned}rho < rcos theta \varphi > \varphi \z recur=rsin theta end{aligned}}	*** *** =rpecado⁡ ⁡ Silencio Silencio φ φ =φ φ z=r#⁡ ⁡ Silencio Silencio {displaystyle {begin{aligned}rho < rsin theta \varphi > \varphi \z recur=rcos theta end{aligned}}

Las coordenadas cilíndricas se pueden convertir en coordenadas esféricas mediante:

Silencio es la elevación:	Silencio es la inclinación:
r=*** *** 2+z2Silencio Silencio =arctan⁡ ⁡ ()z*** *** )φ φ =φ φ {fnMicrosoft }Thetat 'arctan left({tfrac {z}{rho }right)\varphi ' varphi end{aligned}}	r=*** *** 2+z2Silencio Silencio =arctan⁡ ⁡ ()*** *** z)φ φ =φ φ {fnMicrosoft Sans Serif}\Theta > 'arctan left({tfrac {rho }{z}right)\varphi &=varphi end{aligned}} {f} {f}f}\fnMicros}f}\fnMicros}f}f}f}\fnMinun}fnMinun}p]

Elementos de línea y volumen

Ver múltiples integrales para detalles de integración de volumen en coordenadas cilíndricas, y Del en coordenadas cilíndricas y esféricas para fórmulas de cálculo vectorial.

En muchos problemas que involucran coordenadas polares cilíndricas, es útil conocer los elementos de línea y volumen; estos se utilizan en integración para resolver problemas que involucran trayectorias y volúmenes.

El elemento de línea es

dr=d*** *** *** *** ^ ^ +*** *** dφ φ φ φ ^ ^ +dzz^ ^ .{displaystyle mathrm {d} {}=mathrm {d} rho ,{boldsymbol {hat {rho }}+rho ,mathrm {d} varphi ,{boldsymbol {hat {varphi }}}+mathrm {d} z,{boldsymbol {hat {hat {}}}}}}}

El elemento de volumen es

dV=*** *** d*** *** dφ φ dz.{displaystyle mathrm {d} V=rho ,mathrm {d} rho ,mathrm {d} varphi ,mathrm {d} z.}

El elemento de superficie en una superficie de radio constante ρ (un cilindro vertical) es

dS*** *** =*** *** dφ φ dz.{displaystyle mathrm {d} S_{rho }=rho ,mathrm {d} varphi ,mathrm {d} z.}

El elemento de superficie en una superficie de acimut constante φ (un semiplano vertical) es

dSφ φ =d*** *** dz.{displaystyle mathrm {d} S_{varphi }=mathrm {d} rho ,mathrm {d} z.}

El elemento de superficie en una superficie de altura constante z (un plano horizontal) es

dSz=*** *** d*** *** dφ φ .{displaystyle mathrm {d} S_{z}=rho ,mathrm {d} rho ,mathrm {d} varphi.}

El operador del en este sistema conduce a las siguientes expresiones para gradiente, divergencia, rotacional y laplaciano:

Silencio Silencio f=∂ ∂ f∂ ∂ *** *** *** *** ^ ^ +1*** *** ∂ ∂ f∂ ∂ φ φ φ φ ^ ^ +∂ ∂ f∂ ∂ zz^ ^ Silencio Silencio ⋅ ⋅ A=1*** *** ∂ ∂ ∂ ∂ *** *** ()*** *** A*** *** )+1*** *** ∂ ∂ Aφ φ ∂ ∂ φ φ +∂ ∂ Az∂ ∂ zSilencio Silencio × × A=()1*** *** ∂ ∂ Az∂ ∂ φ φ − − ∂ ∂ Aφ φ ∂ ∂ z)*** *** ^ ^ +()∂ ∂ A*** *** ∂ ∂ z− − ∂ ∂ Az∂ ∂ *** *** )φ φ ^ ^ +1*** *** ()∂ ∂ ∂ ∂ *** *** ()*** *** Aφ φ )− − ∂ ∂ A*** *** ∂ ∂ φ φ )z^ ^ Silencio Silencio 2f=1*** *** ∂ ∂ ∂ ∂ *** *** ()*** *** ∂ ∂ f∂ ∂ *** *** )+1*** *** 2∂ ∂ 2f∂ ∂ φ φ 2+∂ ∂ 2f∂ ∂ z2{displaystyle {begin{aligned}nabla f sensible={frac {partial f}{boldsymbol {hat {f} {f} {f}f} {fnf} {fnf} {f}fnf}fnfnKfnKf}f}f}}f}f}}}fnfnf}}fnKfnKfnKfnKfnKfnKf}f}}f}fnKfnfnKf}}}}}}}}}}}}}}}}} { {f} {f} {f} {f} {f}f} {f} {f} {f} {f}}} {f}}}} {f} {f}} {f}f}f} {f} {f} {f} {f}} {f}f}f}f}f}}}}}f}}}}}}f} {f} {f}f}}}}}}}} {f} {f} {f} {f} {f}f}}f}f}}}}f} {f}f} {f} {f} {f} {f}f} {f}f} {\f}f}f}f}f}f}f}}f}f}f}f}f}}}}f}f}}}f} }{boldsymbol {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f} {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnfnMicrosoft {f}fnfnMicrosoft {f}fn\fnfnfnfnfnfnfnfnfnfnfnfnfnfnfn\fnfnfn\\fnfnfnfn\fnfn\\\fnfn\fn\\fnfn\fn\fnfn\\fn\\fnfnfn\\\\\fn\\\\fn {fnK} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {f}}}} {fnMicrosoft} {fnMicrosoft} {fnK} {f}}}}} {f}fnMicroc}} {f}}}}}f} {f} {f}f}}}f}f}f}f}f}f}f}f}f}f} {f}f} {f}f}f}f}f}f}}f}f}}f}f}f}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}}f}fn }{partial varphi }+{frac {partial A_{z}{partial z}[8px]nabla times {boldsymbol {A} {=left({frac {1}{rho {fnMicroc {partial A_{z}}{partial varphi }-{frac {partial A_{varphi}}{partial z}}right){boldsymbol {hat {rho - ¿Qué? {fnMicrosoft Sans} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {f} {f} {f}f} {f}f} {f}f} {f} {f}}}f} {f} {f}f} {f}f}f} {f}f} {f}}f}f}f}f}f}f}f}f}f}f}}f} {f}f} {f}f}f}}}f}f}f}f}f}f}f}f}f}f}f}}f} {f}f} {f}f} {f}f} {f}}f}f}f} {f}f}f}f} {f}f}f}f}f}}f}f}f}f}f}f}f}

Armónicos cilíndricos

Las soluciones de la ecuación de Laplace en un sistema con simetría cilíndrica se denominan armónicos cilíndricos.

Cinemática

En un sistema de coordenadas cilíndricas, la posición de una partícula se puede escribir como

r=*** *** *** *** ^ ^ +zz^ ^ .{fnMicrosoft Sans Serif}+z, {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}

v=drdt=*** *** Í Í *** *** ^ ^ +*** *** φ φ Í Í φ φ ^ ^ +zÍ Í z^ ^ ,{fnK} {fncipi} {fnh} {fnh} {fnh}} {m} {m}} {fn}} {fnh}}fnfnh}, {fnfnfnh00fnfnfnh00fnh00}fn\fnfnfnfnfnfnh00}fnh00fnfnfnfnfnfnfnh00fnh00fnfnfnh00fnfnh00fnh00fnh00}fnhnh00fnfnh00}fnh00}fnh00\fnh00fnh00fnfnh00}fnh00fnfnh00}fnfnh00}\fn }}+rho ,{dot {varphi },{hat {boldsymbol {varphi }+{dot {z},{hat {boldsymbol {Z}}}

*** *** φ φ Í Í φ φ ^ ^ {displaystyle rho {dot {fnfafo }{hat {varphi }

d*** *** ^ ^ dt=φ φ Í Í z^ ^ × × *** *** ^ ^ {displaystyle {frac {mathrm} {fnh} {fnh} {fnh}} {fnh} {fnh} {fnh}}fncipes {fn}}} {fnh}}} {fnfnh00}}}} {fnh00}}}} {fnfnH00}}}} {f}}}}}}}}}}}} {f}}}}}}}}}} {f}}}}} {f} {f}}}}}}} {f}}}} {f}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}} {m}}} {m}}}}}}} {m}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m}}}}}

a=dvdt=()*** *** .. − − *** *** φ φ Í Í 2)*** *** ^ ^ +()2*** *** Í Í φ φ Í Í +*** *** φ φ .. )φ φ ^ ^ +z.. z^ ^ {fnhm} {fnhm} {fnhm {fnhm} {fnhm}} {mhhm {}}}}=lft({ddot {rho }-rho ,{dot {cH00} {ccH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00}cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00}}cH00cH00cH00}cH00cH00cH00cH00cH00}cH00}cH00cH00cH00}cH00cH00cH00cH00cH00 {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnK}} {fnK}} {fnMicrosoft}}