Sistema autónomo (matemáticas)

En matemáticas, un sistema autónomo o ecuación diferencial autónoma es un sistema de ecuaciones diferenciales ordinarias que no depende explícitamente de la variable independiente. Cuando la variable es el tiempo, también se denominan sistemas invariantes en el tiempo.

Muchas leyes de la física, en las que se suele suponer que la variable independiente es el tiempo, se expresan como sistemas autónomos porque se supone que las leyes de la naturaleza que se cumplen ahora son idénticas a las de cualquier punto del pasado o del futuro.

Definición

Un sistema autónomo es un sistema de ecuaciones diferenciales ordinarias de la forma

ddtx()t)=f()x()t)){displaystyle {frac {d}x(t)=f(x(t)}

Se distingue de los sistemas de ecuaciones diferenciales de la forma

ddtx()t)=g()x()t),t){displaystyle {frac {d}{dt}x(t)=g(x(t),t)}

Propiedades

Las soluciones son invariantes bajo traslaciones horizontales:

Vamos x1()t){displaystyle x_{1}(t)} ser una solución única del problema de valor inicial para un sistema autónomo

ddtx()t)=f()x()t)),x()0)=x0.{displaystyle {frac {d}{dt}x(t)=f(x(t)),quad x(0)=x_{0}

x2()t)=x1()t− − t0){displaystyle x_{2}(t)=x_{1}(t-t_{0}

ddtx()t)=f()x()t)),x()t0)=x0.{displaystyle {frac {d}{dt}x(t)=f(x(t)),quad x(t_{0})=x_{0}

s=t− − t0{displaystyle S=t-t_{0}

x1()s)=x2()t){displaystyle x_{1}(s)=x_{2}(t)}

ds=dt{displaystyle ds=dt}

ddtx2()t)=ddtx1()t− − t0)=ddsx1()s)=f()x1()s))=f()x2()t)).{displaystyle {frac {d} {dt}x_{2}(t)={frac {d} {dt}x_{1}(t-t_{0})={frac {d}x_{1}(s)=f(x_{1}(s)=f(x_{2}(t)). }

x2()t0)=x1()t0− − t0)=x1()0)=x0.{displaystyle x_{2}(t_{0})=x_{1}(t_{0}-t_{0})=x_{1}(0)=x_{0}

Ejemplo

La ecuación Sí..=()2− − Sí.)Sí.{displaystyle y'=left(2-yright)y} es autónomo, ya que la variable independiente (x{displaystyle x}) no aparece explícitamente en la ecuación. Para trazar el campo de la pendiente y la isoclina para esta ecuación, se puede utilizar el siguiente código en GNU Octave/MATLAB

Ffun = @(X, Y)2 - Y) . * Y; % función f(x,y)=(2-y)y[X, Y] = meshgrid()0:.2:6, -1:.2:3); % elegir los tamaños de la parcelaDY = Ffun()X, Y); DX = uno()tamaño()DY)); % genera los valores de tramaQuinto()X, Y, DX, DY, 'k '); % trazar el campo de dirección en negroEspera. on;contorno()X, Y, DY, [0 1 2] 'g'); % añadir las isoclines(0 1 2) en verdeTítulo()Campo de pendiente e isoclinas para f(x,y)=(2-y)y ')

Uno puede observar desde la parcela que la función ()2− − Sí.)Sí.{displaystyle left(2-yright)y} es x{displaystyle x}- invariante, y también la forma de la solución, es decir. Sí.()x)=Sí.()x− − x0){displaystyle y(x)=y(x-x_{0} para cualquier cambio x0{displaystyle x_{0}.

Resolviendo la ecuación simbólicamente en MATLAB, ejecutando

Síntesis y(x);ecuación = ()diff()Sí.) == ()2 - Sí.) * Sí.);% resolver la ecuación para una solución general simbólicamenteY_general = dsolve()ecuación);

obtiene dos soluciones de equilibrio, Sí.=0{displaystyle y=0} y Sí.=2{displaystyle y=2}, y una tercera solución que implica una constante desconocida C3{displaystyle C_{3}, -2 / (exp(C3 - 2 * x) - 1).

Recogiendo algunos valores específicos para la condición inicial, uno puede agregar la gráfica de varias soluciones

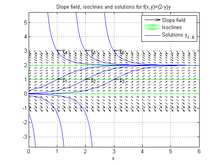
% resolver el problema de valor inicial simbólicamente% para diferentes condiciones inicialesy1 = dsolve()ecuación, Sí.()1) == 1); y2 = dsolve()ecuación, Sí.()2) == 1);y3 = dsolve()ecuación, Sí.()3) == 1); y4 = dsolve()ecuación, Sí.()1) == 3);Y5 = dsolve()ecuación, Sí.()2) == 3); y6 = dsolve()ecuación, Sí.()3) == 3);% trazar las solucionesezplot()y1, [0 6]); ezplot()y2, [0 6]); ezplot()y3, [0 6]);ezplot()y4, [0 6]); ezplot()Y5, [0 6]); ezplot()y6, [0 6]);Título()'Slope field, isoclines and solutions for f(x,y)=(2-y)y ')leyenda()Campo de pendiente ', 'Isoclines ', 'Solutions y_{1..6} ');texto[1 2 3] [1 1 1] strcat()'Leftarrow ', {}'y_1 ', 'y_2 ', 'y_3 '}));texto[1 2 3] [3 3 3] strcat()'Leftarrow ', {}'y_4 ', 'y_5 ', 'y_6 '}));cuadrícula on;

Análisis cualitativo

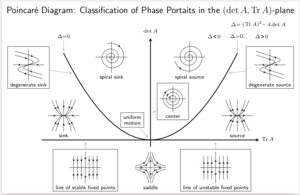
Los sistemas autónomos se pueden analizar cualitativamente utilizando el espacio de fase; en el caso de una variable, esta es la línea de fase.

Técnicas de solución

Las siguientes técnicas se aplican a ecuaciones diferenciales autónomas unidimensionales. Cualquier ecuación unidimensional del orden n{displaystyle n} es equivalente a un n{displaystyle n}- sistema de primer orden dimensional (como se describe en la reducción a un sistema de primer orden), pero no necesariamente viceversa.

Primer pedido

La ecuación autónoma de primer orden

dxdt=f()x){displaystyle {frac {dx}=f(x)}

t+C=∫ ∫ dxf()x){displaystyle t+C=int {f}}}

Segunda orden

La ecuación autónoma de segundo orden

d2xdt2=f()x,x.){displaystyle {frac {d^{2}x}{dt}=f(x,x)}

v=dxdt{displaystyle v={frac {dx} {dt}}

x{displaystyle x}

d2xdt2=dvdt=dxdtdvdx=vdvdx{displaystyle {frac {f}x}{dt^{2}={frac}}={frac} {fn} {fnK} {f}} {fnK}} {f}}}=v{frac {dx}} {f}}} {f}}} {f}}} {f}} {f}}} {f}}} {f}}}}}} {f}}}}} {f}}}}}} {f}}}}}} {f}}}}} {f}}}}}}}}}} {f} {f}}}}} {f}}} {f}}}}}}} {f}}}}}}}} {f}}}}}}}} {f}}}}}}}}}}}} {f}}}} {f}} {f}}}} {f}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}

vdvdx=f()x,v){displaystyle v{frac {dx}=f(x,v)}

t{displaystyle t}

v{displaystyle v}

x{displaystyle x}

v{displaystyle v}

dxdt=v()x)⇒ ⇒ t+C=∫ ∫ dxv()x){displaystyle {frac {dx}{dt}=v(x)quad Rightarrow quad t+C=int {frac {dx}{v(x)}}}

que es una solución implícita.

Caso especial: x″ = f(x)

El caso especial donde f{displaystyle f} es independiente de x.{displaystyle x'}

d2xdt2=f()x){displaystyle {frac {d^{2}x}{dt}=f(x)}

beneficios del tratamiento por separado. Este tipo de ecuaciones son muy comunes en la mecánica clásica porque siempre son sistemas hamiltonianos.

La idea es hacer uso de la identidad

dxdt=()dtdx)− − 1{displaystyle {frac {dx}{dt}=left({frac {dt}right)}{-1}}

que se deriva de la regla de la cadena, salvo cualquier problema debido a la división por cero.

Al invertir ambos lados de un sistema autónomo de primer orden, se puede integrar inmediatamente con respecto a x{displaystyle x}:

dxdt=f()x)⇒ ⇒ dtdx=1f()x)⇒ ⇒ t+C=∫ ∫ dxf()x){displaystyle {frac {dx}=f(x)quad Rightarrow quad {frac {dt}{dx}={frac {1}{f(x)}quad Rightarrow quad t+C=int {frac {dx}{f(x)}}}

que es otra manera de ver la separación de la técnica de variables. El segundo derivado debe ser expresado como un derivado con respecto a x{displaystyle x} en lugar de t{displaystyle t}:

d2xdt2=ddt()dxdt)=ddx()dxdt)dxdt=ddx()()dtdx)− − 1)()dtdx)− − 1=− − ()dtdx)− − 2d2tdx2()dtdx)− − 1=− − ()dtdx)− − 3d2tdx2=ddx()12()dtdx)− − 2){displaystyle {begin{aligned}{2}x}{dt^{2}}} {frac}{frac} {f}}} {f}}}}} {f}} {fnK}} {f}}} {f}}} {d} {dt}left({frac {dx} {dt}right)={frac} {fnMicroc} {fnMicroc {fnMicroc} {fnMicroc {dx}}[4pt] {dx}dx}left({frac {dt}right)^{-1}right)left({frac {dt}{dx}right)^{-1}[4pt] â=-left({dt}{dx}right)}{-2}{}{-2}{dx}{}{dx}{}}}}{}{}}}}}}{}{}}}{}{dx}{}}}}}}}{}}}}}}{}}{}{dx}}}}}}}}{}}}}}}}}}}}}}{}}}}}}}{}{}}{}}{}}{}}}}{}}}}{dx}}}}}{}}}}}}}}}}}}}}}}}{}}}}}}}}}}}}{}}}}}}}}}}}}}}} {fnK} {fnMicroc} {fnK}} {fnMicroc}} {fnK}} {f}} {fn} {f}}}} {fnK}}}}}} {f}}} {f}}}} {f}}} {f}}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}p}}}}}}}}}}}}}}ppppppppppb}b}}}}}}}}}}ppppppppppppb}pppppppppppppppb}pppppb}pb} {fnMicroc {fnMicroc}}right)}{-3}{frac {fnMicroc}}right)}{-3}{frac {fnMicrosoft Sans Serif} {dx}left({frac} {1}{2}left({frac {dt}right)}end{aligned}}}}

Para volver a enfatizar: lo que se ha logrado es que el segundo derivado con respecto a t{displaystyle t} ha sido expresado como un derivado de x{displaystyle x}. La ecuación original de segundo orden ahora se puede integrar:

d2xdt2=f()x)ddx()12()dtdx)− − 2)=f()x)()dtdx)− − 2=2∫ ∫ f()x)dx+C1dtdx=± ± 12∫ ∫ f()x)dx+C1t+C2=± ± ∫ ∫ dx2∫ ∫ f()x)dx+C1{displaystyle {begin{aligned}{frac {d^{2}{2}}} {f(x)\\\\fnMic} {dx}left({frac} {1}{2}}left({frac {dx}right)}{-2}right) â=f(x)\\\left({frac {dt}}right)}{-2} {=2int f(x)dx+C_{1}\{f} {dx}}}} {f}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}} {p}}}}}}}}}} {c}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}c}}}c}c}c}}}}}}}}}}}}c}}}}}}}}}}c}}}}}}}}}}}}}}}} {fnMicroc {1}\t+C_{2}} {fnMicroc {dx} {f} {fn} {fnK} {fnMicroc {sqrt {2int f(x)dx+C_{1}}}}}}}end{aligned}}}}}}}}}} {f}}}}}}}}}} {f}}}}}}}} {f}}}}}}} {f} {f}}}}}} {f}}} {f}}}}}}} {f}}}}}}}} {f}}}}}}} {f}}}}}}}}}}}}}}}}}}} {f}}} {f}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Esta es una solución implícita. El mayor problema potencial es la incapacidad para simplificar las integrales, lo que implica dificultad o imposibilidad en la evaluación de las constantes de integración.

Caso especial: x″ = x′n f(x)

Usando el enfoque anterior, la técnica puede extenderse a la ecuación más general

d2xdt2=()dxdt)nf()x){displaystyle {frac {d^{2}x}{dt^{2}=left({frac {dx}{dt}}right)}{n}f(x)}

Donde n{displaystyle n} es un parámetro no igual a dos. Esto funcionará ya que el segundo derivado se puede escribir en una forma que implica un poder x.{displaystyle x'}. Reescribir el segundo derivado, reorganizar y expresar el lado izquierdo como un derivado:

− − ()dtdx)− − 3d2tdx2=()dtdx)− − nf()x)− − ()dtdx)n− − 3d2tdx2=f()x)ddx()12− − n()dtdx)n− − 2)=f()x)()dtdx)n− − 2=()2− − n)∫ ∫ f()x)dx+C1t+C2=∫ ∫ ()()2− − n)∫ ∫ f()x)dx+C1)1n− − 2dx{displaystyle {begin{aligned} âTMa âTMa {frac {dt}right)}{-3}{frac {fnK} {fnMicroc}=fnMicroc {dt}{dx}right)}{-n}f(x)[4pt] limitada-left({frac {dt}{dx}}right)}{n-3}{frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {}}left({frac] {1}{2-n}left({frac {dt}{dx}right)=f(x)[4pt] âleft({frac {dt}dx}derecha)}{n-2}=(2-n)int f(x)dx+C_{1}{2}{2}cc}{2}c}}c}}{2}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}cc}ccc}c}c}cccc}ccc}c}c}c}cc}c}ccc}c}ccc}cc {1}{n-2}dxend{aligned}}}

La derecha tendrá +/ - si n{displaystyle n} es incluso. El tratamiento debe ser diferente si n=2{displaystyle n=2}:

− − ()dtdx)− − 1d2tdx2=f()x)− − ddx()In⁡ ⁡ ()dtdx))=f()x)dtdx=C1e− − ∫ ∫ f()x)dxt+C2=C1∫ ∫ e− − ∫ ∫ f()x)dxdx{displaystyle {begin{aligned}-left({frac {dt}right)}{-1}{frac {d^{2}t}{dx^{2}} {f(x)\ {d}{dx}left(lnleft({frac {dt}{dx}right)right) {f(x)\\\{fracf} {dt}{dx} {=C_{1}e^{-int f(x)dx}\t+C_{2} {=C_{1}int e^{-int f(x)dx}dxend{aligned}}

Órdenes superiores

No existe un método análogo para resolver ecuaciones autónomas de orden superior o tercero. Tales ecuaciones solo se pueden resolver exactamente si tienen alguna otra propiedad simplificadora, por ejemplo, linealidad o dependencia del lado derecho de la ecuación solo de la variable dependiente (es decir, no de sus derivadas). Esto no debería sorprender, considerando que los sistemas autónomos no lineales en tres dimensiones pueden producir un comportamiento verdaderamente caótico como el atractor de Lorenz y el atractor de Rössler.

Del mismo modo, las ecuaciones generales no autónomas de segundo orden son irresolubles explícitamente, ya que estas también pueden ser caóticas, como en un péndulo periódicamente forzado.

Caso multivariante

In x.()t)=Ax()t){displaystyle mathbf {x} '(t)=Amathbf {x} (t)}, donde x()t){displaystyle mathbf {x} (t)} es un n{displaystyle n}-dimensional vector de columna dependiente t{displaystyle t}.

La solución es x()t)=eAtc{displaystyle mathbf {x} (t)=e^{At}mathbf {c} Donde c{displaystyle mathbf {c} es un n× × 1{displaystyle ntimes 1} vector constante.

Duración finita

Para las EDO autónomas no lineales, es posible, bajo algunas condiciones, desarrollar soluciones de duración finita, lo que significa que, a partir de su propia dinámica, el sistema alcanzará el valor cero en un tiempo final y permanecerá allí en cero para siempre. Estas soluciones de duración finita no pueden ser funciones analíticas en toda la línea real, y debido a que no serán funciones de Lipschitz en el tiempo final, no soportan la unicidad de las soluciones de las ecuaciones diferenciales de Lipschitz.

Como ejemplo, la ecuación:

Sí..=− − Sgn()Sí.)SilencioSí.Silencio,Sí.()0)=1{displaystyle y'=-{text{sgn}(y){sqrt ¿Qué?

Admite la solución de duración finita:

Sí.()x)=14()1− − x2+Silencio1− − x2Silencio)2{displaystyle y(x)={4}left(1-{frac] {x}{2}+left habit1-{frac {x}{2}right sobre la vidaright)} {2}}