Silogismo hipotético

En lógica clásica, un silogismo hipotético es una forma de argumento válida, un silogismo con una declaración condicional para una o ambas de sus premisas.

Hay cuatro posibles formas de silogismos hipotéticos, dos de los cuales son válidos, mientras que dos son inválidos. Considerando un ejemplo muy simple puede ayudarle a entender por qué estas formas son válidas o inválidas. Si "p" representa "Candiru es un pez" y "q" representa "Candiru tiene ginebras", trate de convencerse a sí mismo reemplazando estas declaraciones por p y q en la tabla anterior.

Un ejemplo en inglés:

Si no me despierto, entonces no puedo ir al trabajo.

Si no puedo ir al trabajo, entonces no me pagarán.

Por lo tanto, si no despierto, entonces no me pagarán.

El término se originó con Teofrasto.

Un silogismo hipotético puro es un silogismo en el que tanto las premisas como las conclusiones son condicionales. El antecedente de una premisa debe coincidir con el consecuente de la otra para que el condicional sea válido. En consecuencia, los condicionales contienen antecedente permanecido como antecedente y consecuente permanecido como consecuente.

Si p, entonces q.

Si q, entonces r.

▪ Si p, entonces r.

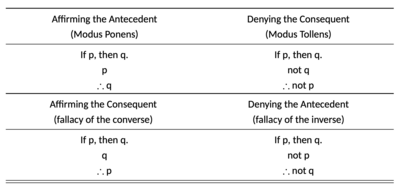
Un silogismo hipotético mixto consta de un enunciado condicional y un enunciado que expresa afirmación o negación con el antecedente o la consecuencia de ese condicional. Por lo tanto, tal silogismo hipotético mixto tiene cuatro formas posibles, de las cuales dos son válidas, mientras que las otras dos no son válidas (Ver Tabla). La primera forma de obtener una conclusión válida es afirmar el antecedente. Un silogismo hipotético válido niega el consecuente (modus tollens) o afirma el antecedente (modus ponens).

Lógica proposicional

En lógica proposicional, silogismo hipotético es el nombre de una regla de inferencia válida (a menudo abreviada HS y a veces también llamada argumento en cadena, regla de la cadena, o el principio de transitividad de la implicación). La regla puede enunciarse:

P→ → Q,Q→ → R▪ ▪ P→ → R{displaystyle {frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}f}f}f}f}fnMicrocfnMicrosoft Sansigual}f}fnMicrosoft Sansigual}f}fnMicrosoft Sansigual}fnMicrosoft Sansigual vez {f}fnMicrosoft Sansigual}fnMicrosoft Sansigual vez {fnKf}}fnMicrosoft Sansigual vez {fnMicrosoft Sansigual vez {fnMicrosoft Sansigually}f}f}f}}f}fn Pto R}

donde la regla es que cada instancia de "P→ → Q{displaystyle Pto Q}", y "Q→ → R{displaystyle Qto R}"parecen en líneas de una prueba, "P→ → R{displaystyle Pto R}"se puede colocar en una línea posterior.

El silogismo hipotético está estrechamente relacionado y es similar al silogismo disyuntivo, ya que también es un tipo de silogismo y también el nombre de una regla de inferencia.

Aplicabilidad

La regla del silogismo hipotético se mantiene en la lógica clásica, la lógica intuicionista, la mayoría de los sistemas de lógica de relevancia y muchos otros sistemas de lógica. Sin embargo, no se cumple en todas las lógicas, incluidas, por ejemplo, la lógica no monótona, la lógica probabilística y la lógica por defecto. La razón de esto es que estas lógicas describen un razonamiento rebatible, y los condicionales que aparecen en contextos del mundo real generalmente permiten excepciones, suposiciones predeterminadas, condiciones ceteris paribus o simplemente incertidumbre.

Un ejemplo, derivado de Ernest W. Adams,

1. Si Jones gana la elección, Smith se retirará después de la elección.
2. Si Smith muere antes de la elección, Jones ganará la elección.
3. Si Smith muere antes de la elección, Smith se retirará después de la elección.

Claramente, (3) no se sigue de (1) y (2). (1) es cierto por defecto, pero no se cumple en las circunstancias excepcionales de la muerte de Smith. En la práctica, los condicionales del mundo real siempre tienden a implicar supuestos o contextos predeterminados, y puede ser inviable o incluso imposible especificar todas las circunstancias excepcionales en las que podrían no ser ciertos. Por razones similares, la regla del silogismo hipotético no se cumple para los condicionales contrafácticos.

Notación formal

La regla de inferencia del silogismo hipotético puede escribirse en notación secuencial, lo que equivale a una especialización de la regla de corte:

P⊢ ⊢ QQ⊢ ⊢ RP⊢ ⊢ R{fnK}

Donde ⊢ ⊢ {displaystyle vdash } es un símbolo metalógico y A⊢ ⊢ B{displaystyle Avdash B} significa que B{displaystyle B} es una consecuencia sintáctica de A{displaystyle A} en algún sistema lógico;

y expresado como una tautología funcional veritativa o teorema de lógica proposicional:

()()P→ → Q)∧ ∧ ()Q→ → R))→ → ()P→ → R){displaystyle (Pto Q)land (Qto R)to (Pto R)}

Donde P{displaystyle P}, Q{displaystyle Q}, y R{displaystyle R. son propuestas expresadas en algún sistema formal.

Prueba

Paso	Proposición	Derivación
1	P→ → Q{displaystyle Pto Q}	Dado
2	Q→ → R{displaystyle Qto R}	Dado
3	P{displaystyle P}	Hipótesis de prueba condicional
4	Q{displaystyle Q}	Modus ponens (1,3)
5	R{displaystyle R.	Modus ponens (2,4)
6	P→ → R{displaystyle Pto R}	Prueba condicional (3-5)

Formas alternativas

Una forma alternativa de silogismo hipotético, más útil para los sistemas clásicos de cálculo proposicional con implicación y negación (es decir, sin el símbolo de la conjunción), es la siguiente:

(HS1) ()Q→ → R)→ → ()()P→ → Q)→ → ()P→ → R)){displaystyle (Qto R)to (Pto Q)to (Pto R)}

Otra forma más es:

(HS2) ()P→ → Q)→ → ()()Q→ → R)→ → ()P→ → R)){displaystyle (Pto Q)to (Qto R)to (Pto R)}

Prueba

A continuación se proporciona un ejemplo de las demostraciones de estos teoremas en tales sistemas. Usamos dos de los tres axiomas usados en uno de los sistemas populares descritos por Jan Łukasiewicz. Las pruebas se basan en dos de los tres axiomas de este sistema:

(A1) φ φ → → ()↑ ↑ → → φ φ ){displaystyle phi to left(psi to phi right)}

(A2) ()φ φ → → ()↑ ↑ → → .. ))→ → ()()φ φ → → ↑ ↑ )→ → ()φ φ → → .. )){displaystyle left(phi to left(psi rightarrow xi right)right)to left(left(phi to psi right)to left(phi to xi right)right)}

La prueba de (HS1) es la siguiente:

1) ()()p→ → ()q→ → r))→ → ()()p→ → q)→ → ()p→ → r)))→ → ()()q→ → r)→ → ()()p→ → ()q→ → r))→ → ()()p→ → q)→ → ()p→ → r)))){displaystyle ((pto (qto r)))to ((pto q)to (pto r))))to ((qto r)to ((pto (qto r))))to ((pto q)to (pto r)))))}}} (instancia de (A1))

2) ()p→ → ()q→ → r))→ → ()()p→ → q)→ → ()p→ → r)){displaystyle (pto (qto r))to (pto q)to (pto r)} (A2))

3) ()q→ → r)→ → ()()p→ → ()q→ → r))→ → ()()p→ → q)→ → ()p→ → r))){displaystyle (qto r)to (pto (qto r))to (pto q)to (pto r))} (de (1) y 2) por modus ponens)

4) ()()q→ → r)→ → ()()p→ → ()q→ → r))→ → ()()p→ → q)→ → ()p→ → r))))→ → ()()()q→ → r)→ → ()p→ → ()q→ → r)))→ → ()()q→ → r)→ → ()()p→ → q)→ → ()p→ → r)))){displaystyle ((qto r)to (pto (qto r))to ((pto q)to (pto r)))))to (((qto r)to (pto (qto r))))))to ((qto r)to ((pto q)to (pto r) (A2))

5) ()()q→ → r)→ → ()p→ → ()q→ → r)))→ → ()()q→ → r)→ → ()()p→ → q)→ → ()p→ → r))){displaystyle (qto r)to (pto (qto r))))to ((qto r)to ((pto q)to (pto r))} (de 3) y 4) por modus ponente)

(6) ()q→ → r)→ → ()p→ → ()q→ → r)){displaystyle (qto r)to (pto (qto r)} (instancia de (A1))

(7) ()q→ → r)→ → ()()p→ → q)→ → ()p→ → r)){displaystyle (qto r)to (pto q)to (pto r)} (de 5) y (6) por modus ponens)

La prueba de (HS2) se proporciona aquí.

Como metateorema

Cada vez que tenemos dos teoremas de la forma T1=()Q→ → R){displaystyle T_{1}=(Qto R)} y T2=()P→ → Q){displaystyle T_{2}=(Pto Q)}, podemos probar ()P→ → R){displaystyle (Pto R)} por los siguientes pasos:

1) ()Q→ → R)→ → ()()P→ → Q)→ → ()P→ → R))){displaystyle (Qto R)to (Pto Q)to (Pto R)} (Posición del teorema probada arriba)

2) Q→ → R{displaystyle Qto R} (instancia de (T1))

3) ()P→ → Q)→ → ()P→ → R){displaystyle (Pto Q)to (Pto R)} (de (1) y 2) por modus ponens)

4) P→ → Q{displaystyle Pto Q} (instancia de (T2))

5) P→ → R{displaystyle Pto R} (de 3) y 4) por modus ponente)