Series de Fourier
Una serie de Fourier () es una suma de funciones sinusoidales armónicamente relacionadas, también conocidas como componentes o armónicos. El resultado de la suma es una función periódica cuya forma funcional está determinada por las opciones de duración del ciclo (o período), el número de componentes y sus amplitudes y parámetros de fase. Con las opciones adecuadas, se puede hacer que un ciclo (o período) de la suma se aproxime a una función arbitraria en ese intervalo (o la función completa si también es periódica). El número de componentes es teóricamente infinito, en cuyo caso se pueden elegir los otros parámetros para hacer que la serie converja a casi cualquier función periódica de buen comportamiento (consulte Prueba patológica y de Dirichlet-Jordan). Los componentes de una función particular están determinados por las técnicas de análisis descritas en este artículo. A veces, primero se conocen los componentes y se sintetiza la función desconocida. por una serie de Fourier. Tal es el caso de una transformada de Fourier en tiempo discreto.
La convergencia de la serie de Fourier significa que a medida que se suman más y más componentes de la serie, cada suma sucesiva de serie parcial de Fourier se aproximará mejor a la función y la igualará con un número potencialmente infinito de componentes Las pruebas matemáticas para esto pueden denominarse colectivamente como el Teorema de Fourier (ver § Convergencia). Las siguientes figuras ilustran algunos resultados de series de Fourier parciales para los componentes de una onda cuadrada.
Una onda cuadrada (representada como el punto azul) se aproxima por su sexta suma parcial (representada como el punto púrpura), formada por resumir los primeros seis términos (representados como flechas) de la serie Fourier de la onda cuadrada. Cada flecha comienza en la suma vertical de todas las flechas a su izquierda (es decir, la suma parcial anterior).
Otra técnica de análisis (no cubierta aquí), adecuada tanto para funciones periódicas como no periódicas, es la transformada de Fourier, que proporciona un continuo de frecuencia de información de componentes. Pero cuando se aplica a una función periódica, todos los componentes tienen amplitud cero, excepto en las frecuencias armónicas. La transformada inversa de Fourier es un proceso de síntesis (como la serie de Fourier), que convierte la información del componente (a menudo conocida como representación en el dominio de la frecuencia) nuevamente en su representación en el dominio del tiempo.
Desde la época de Fourier, se han descubierto muchos enfoques diferentes para definir y comprender el concepto de serie de Fourier, todos los cuales son coherentes entre sí, pero cada uno de los cuales enfatiza diferentes aspectos del tema. Algunos de los enfoques más poderosos y elegantes se basan en ideas y herramientas matemáticas que no estaban disponibles en la época de Fourier. Fourier definió originalmente la serie de Fourier para funciones de valores reales de argumentos reales y utilizó las funciones de seno y coseno como base para la descomposición. Desde entonces, se han definido muchas otras transformadas relacionadas con Fourier, extendiendo su idea inicial a muchas aplicaciones y dando origen a un área de las matemáticas llamada análisis de Fourier.
Proceso de análisis
Esta sección describe el proceso de análisis que deriva los parámetros de una serie Fourier que aproxima una función conocida, Un ejemplo de sintetización de una función desconocida de los parámetros conocidos es la transformación de Fourier discreta.
Formas comunes
La serie Fourier se puede representar en diferentes formas. El amplitud-fase formulario, sine-cosina forma, y exponencial forma se utilizan comúnmente y se expresan aquí para una función de valor real . (Ver § Funciones de valor complejo y § Otras notaciones comunes para formas alternativas).
El número de términos resumidos, , es un número potencialmente infinito. Incluso así, la serie podría no converger o exactamente equipararse a en todos los valores de (como una discontinuidad de un solo punto) en el intervalo de análisis. Para las funciones bien interpretadas típicas de los procesos físicos, la igualdad se asume habitualmente, y las condiciones Dirichlet proporcionan condiciones suficientes.
El índice entero, , es también el número de ciclos el armónico hace en el período de la función . Por lo tanto:
- El la longitud de onda de armónico es y en unidades .
- El frecuencia armónica es y en unidades recíprocas de .

Forma amplitud-fase
La serie de Fourier en forma de fase de amplitud es:
()Eq.1) |
- Es... armónico .
- es la amplitud y la amplitud armónica es su cambio de fase.
- La frecuencia fundamental es el término para cuando iguales 1, y puede ser referido como armónico.
- a veces se llama componente armónico o DC. Es el valor medio de .
Claramente Eq.1 puede representar funciones que son sólo una suma de una o más de las frecuencias armónicas. Lo notable, para aquellos que aún no conocen este concepto, es que también puede representar las frecuencias intermedias y/o funciones no sinusoidales debido al número potencialmente infinito de términos ().

Los coeficientes y puede ser entendido y derivado en términos de la cruz-correlación entre y un sinusoide a frecuencia . Para una frecuencia general y un intervalo de análisis la función transversal-correlación:
()Eq.2) |
es esencialmente un filtro igualado, con plantilla . El máximo es una medida de la amplitud de frecuencia en la función , y el valor de al máximo determina la fase de esa frecuencia. La Figura 2 es un ejemplo, donde es una onda cuadrada (no mostrada), y frecuencia es armónico. También es un ejemplo de derivar el máximo de sólo dos muestras, en lugar de buscar toda la función. Esto es posible por una identidad trigonométrica:
()Eq.3) |
Combinando esto con Eq.2 da:
que introduce las definiciones de y . Y tomamos nota para referencia posterior que y se puede simplificar:
Por lo tanto y son las coordenadas rectangulares de un vector con coordenadas polares y
Forma seno-coseno
Sustituyendo Ec.3 en Eq.1 da:
En términos de las cantidades fácilmente calculadas, y , recuerde que:
Por lo tanto, una forma alternativa de la serie de Fourier, utilizando las coordenadas rectangulares, es la forma seno-coseno:
()Eq.4) |
Forma exponencial
Otra identidad aplicable es la fórmula de Euler:
(Nota: el ∗ denota conjugación compleja).
Por lo tanto, con definiciones:
el resultado final es:
()Eq.5) |
Esta es la forma consuetudinaria para generalizar a § Funciones de valor complejo. Valores negativos de corresponde a la frecuencia negativa (explicada en Fourier transforma § Uso de sinusoides complejos para representar verdaderos sinusoides).
Ejemplo
Considere una función de diente de sierra:
En este caso, los coeficientes de Fourier vienen dados por
Se puede demostrar que la serie Fourier converge a en cada punto Donde es diferente, y por lo tanto:
()Eq.6)
Cuando , la serie Fourier converge a 0, que es la mitad de la suma del límite izquierdo y derecho de s a . Este es un caso particular del teorema Dirichlet para la serie Fourier.
Este ejemplo conduce a una solución del problema de Basilea.
Convergencia
Una demostración de que una serie de Fourier es una representación válida de cualquier función periódica (que satisfaga las condiciones de Dirichlet) se describe en § Teorema de Fourier que demuestra la convergencia de la serie de Fourier.
En aplicaciones de ingeniería, la serie Fourier generalmente se presume que converge casi en todas partes (las excepciones que están en discontinuidades discretas) ya que las funciones encontradas en la ingeniería son mejores que las funciones que los matemáticos pueden proporcionar como contra-examples a esta presunción. En particular, si es continuo y el derivado de (que puede no existir en todas partes) es cuadrado integrador, luego la serie Fourier converge absolutamente y uniformemente a . Si una función es cuadrada-integrable en el intervalo , entonces la serie Fourier converge a la función en casi todos los puntos. Es posible definir coeficientes Fourier para funciones o distribuciones más generales, en tales casos la convergencia en la norma o la convergencia débil es generalmente de interés.
Funciones de valores complejos
Si es una función de valor complejo de una variable real ambos componentes (parte real e imaginaria) son funciones de valor real que pueden ser representadas por una serie Fourier. Los dos conjuntos de coeficientes y la suma parcial son dados por:
- y
Definición rendimientos:
()Eq.7) |
Esto es idéntico a Eq.5 excepto y ya no son conjugados complejos. La fórmula para es también invariable:
Otras notaciones comunes
La notación es insuficiente para discutir los coeficientes Fourier de varias funciones diferentes. Por lo tanto, es reemplazado por una forma modificada de la función (, en este caso), como o , y notación funcional a menudo reemplaza subscripting:
En ingeniería, especialmente cuando la variable representa tiempo, la secuencia de coeficiente se llama una representación de dominio de frecuencia. Los corchetes se utilizan a menudo para enfatizar que el dominio de esta función es un conjunto discreto de frecuencias.
Otra representación de dominio de frecuencia de uso común utiliza los coeficientes de la serie de Fourier para modular un peine de Dirac:
Donde representa un dominio de frecuencia continua. Cuando variable tiene unidades de segundos, tiene unidades de hertz. Los "tetos" del peine son espaciados en múltiplos (es decir, armónicos) de , que se llama la frecuencia fundamental. puede ser recuperado de esta representación por un inverso Fourier transform:
La función construida es, por lo tanto, comúnmente conocido como Transformación de Fourier, aunque el Fourier integral de una función periódica no es convergente en las frecuencias armónicas.
Historia
La serie de Fourier recibe su nombre en honor a Jean-Baptiste Joseph Fourier (1768–1830), quien hizo importantes contribuciones al estudio de las series trigonométricas, después de las investigaciones preliminares de Leonhard Euler, Jean le Rond d'Alembert y Daniel Bernoulli. Fourier introdujo la serie con el propósito de resolver la ecuación del calor en una placa de metal, publicando sus resultados iniciales en su Mémoire sur la propagation de la chaleur dans les corps solides de 1807 (Tratado sobre la propagación del calor en cuerpos sólidos), y publicando su Théorie analytique de la chaleur (Teoría analítica del calor) en 1822. La Mémoire introdujo el análisis de Fourier, específicamente las series de Fourier. A través de la investigación de Fourier se estableció el hecho de que una función arbitraria (al principio, continua y luego generalizada a cualquier parte suave) puede ser representada por una serie trigonométrica. El primer anuncio de este gran descubrimiento lo hizo Fourier en 1807, ante la Academia Francesa. Las primeras ideas de descomponer una función periódica en la suma de funciones oscilantes simples se remontan al siglo III a. C., cuando los antiguos astrónomos propusieron un modelo empírico de movimientos planetarios, basado en deferentes y epiciclos.
La ecuación del calor es una ecuación diferencial parcial. Antes del trabajo de Fourier, no se conocía ninguna solución a la ecuación del calor en el caso general, aunque sí se conocían soluciones particulares si la fuente de calor se comportaba de manera simple, en particular, si la fuente de calor era una onda seno o coseno.. Estas soluciones simples ahora a veces se llaman soluciones propias. La idea de Fourier era modelar una fuente de calor complicada como una superposición (o combinación lineal) de ondas seno y coseno simples, y escribir la solución como una superposición de las soluciones propias correspondientes. Esta superposición o combinación lineal se denomina serie de Fourier.
Desde un punto de vista moderno, los resultados de Fourier son algo informales, debido a la falta de una noción precisa de función e integral a principios del siglo XIX. Posteriormente, Peter Gustav Lejeune Dirichlet y Bernhard Riemann expresaron los resultados de Fourier con mayor precisión y formalidad.
Aunque la motivación original era resolver la ecuación del calor, más tarde se hizo evidente que las mismas técnicas se podían aplicar a una amplia gama de problemas matemáticos y físicos, y especialmente a aquellos que involucraban ecuaciones diferenciales lineales con coeficientes constantes, para los cuales las soluciones propias son sinusoides. La serie de Fourier tiene muchas aplicaciones de este tipo en ingeniería eléctrica, análisis de vibraciones, acústica, óptica, procesamiento de señales, procesamiento de imágenes, mecánica cuántica, econometría, teoría de capas, etc.
Comienzos
Joseph Fourier escribió:
Multiplicar ambos lados por , y luego la integración de a rendimientos:
—Joseph Fourier, Mémoire sur la propagation de la chaleur dans les corps solides. (1807)
Esto da inmediatamente cualquier coeficiente ak de la serie trigonométrica para φ(y) para cualquier función que tenga tal expansión. Funciona porque si φ tiene tal expansión, entonces (bajo supuestos de convergencia adecuados) la integral
En estas pocas líneas, que se acercan al formalismo moderno utilizado en las series de Fourier, Fourier revolucionó tanto las matemáticas como la física. Aunque Euler, d'Alembert, Daniel Bernoulli y Gauss utilizaron previamente series trigonométricas similares, Fourier creía que tales series trigonométricas podían representar cualquier función arbitraria. En qué sentido eso es realmente cierto es una cuestión un tanto sutil y los intentos durante muchos años por aclarar esta idea han llevado a importantes descubrimientos en las teorías de convergencia, espacios funcionales y análisis armónico.
Cuando Fourier presentó un ensayo de competencia posterior en 1811, el comité (que incluía a Lagrange, Laplace, Malus y Legendre, entre otros) concluyó: ... la forma en que el autor llega a estas ecuaciones no está exenta de dificultades y... su análisis para integrarlas todavía deja algo que desear en cuanto a generalidad e incluso rigor.
La motivación de Fourier
La expansión de la serie Fourier de la función de la sierra (arriba) se ve más complicada que la fórmula simple , por lo que no es inmediatamente evidente por qué uno necesita la serie Fourier. Mientras hay muchas aplicaciones, la motivación de Fourier fue en resolver la ecuación de calor. Por ejemplo, considere una placa de metal en forma de un cuadrado cuya medida metros, con coordenadas . Si no hay fuente de calor dentro de la placa, y si tres de los cuatro lados se sostienen a 0 grados Celsius, mientras que el cuarto lado, dado por , se mantiene en el gradiente de temperatura grados Celsius, para dentro , entonces se puede demostrar que la distribución de calor estacionaria (o la distribución de calor después de un largo período de tiempo ha pasado)
Aquí, sinh es la función sine hiperbólica. Esta solución de la ecuación de calor se obtiene multiplicando cada término de Eq.6 por . Mientras nuestra función de ejemplo Parece tener una serie Fourier innecesariamente complicada, la distribución de calor no es trivial. La función no puede ser escrito como una expresión de forma cerrada. Este método de resolver el problema del calor fue posible por el trabajo de Fourier.
Animación de series complejas de Fourier
Un ejemplo de la capacidad de la serie compleja de Fourier para trazar cualquier figura cerrada bidimensional se muestra en la animación adyacente de la serie compleja de Fourier que traza la letra 'e' (para exponencial). Tenga en cuenta que la animación utiliza la variable 't' para parametrizar la letra 'e' en el plano complejo, lo que equivale a utilizar el parámetro 'x' en la subsección de este artículo sobre funciones de valores complejos.
En el plano posterior de la animación, los vectores giratorios se agregan en un orden que alterna entre un vector que gira en sentido positivo (en sentido contrario a las agujas del reloj) y un vector que gira en la misma frecuencia pero en sentido negativo (en sentido horario). dirección, lo que resulta en un solo brazo trazador con muchos zigzags. Esta perspectiva muestra cómo la suma de cada par de vectores giratorios (uno que gira en dirección positiva y otro en dirección negativa) empuja el trazo anterior (que se muestra como una línea punteada de color gris claro) más cerca de la forma de la letra 'e'.
En el plano frontal de la animación, los vectores giratorios se agregan en dos conjuntos, el conjunto de todos los vectores giratorios positivos y el conjunto de todos los vectores giratorios negativos (el componente no giratorio se divide uniformemente entre el dos), lo que da como resultado dos brazos trazadores que giran en direcciones opuestas. El pequeño círculo de la animación indica el punto medio entre los dos brazos y también el punto medio entre el origen y el punto de rastreo actual indicado por '+'. Esta perspectiva muestra cómo la serie compleja de Fourier es una extensión (la suma de un brazo) de la serie geométrica compleja que tiene un solo brazo. También muestra cómo los dos brazos se coordinan entre sí. Por ejemplo, como el punto de rastreo gira en la dirección positiva, el brazo de la dirección negativa permanece estacionado. De manera similar, cuando el punto de rastreo gira en dirección negativa, el brazo de dirección positiva permanece estacionado.
Entre los planos posterior y frontal de la animación hay trapecios giratorios cuyas áreas representan los valores de los términos complejos de la serie de Fourier. Esta perspectiva muestra la amplitud, la frecuencia y la fase de los términos individuales de la serie compleja de Fourier en relación con la suma de la serie que converge espacialmente a la letra 'e' en los planos trasero y delantero. Los canales izquierdo y derecho de la pista de audio corresponden respectivamente a los componentes real e imaginario del punto de rastreo actual '+' pero aumentado en frecuencia por un factor de 3536 para que la frecuencia fundamental de la animación (n=1) sea un tono de 220 Hz (A220).
Otras aplicaciones
La transformada de Fourier en tiempo discreto es un ejemplo de una serie de Fourier.
Otra aplicación es resolver el problema de Basilea usando el teorema de Parseval. El ejemplo se generaliza y se puede calcular ζ(2n), para cualquier entero positivon.
Tabla de series comunes de Fourier
En la siguiente tabla se muestran algunos pares comunes de funciones periódicas y sus coeficientes de serie de Fourier.
- designa una función periódica definida en .
- designar los coeficientes de la serie Fourier (forma sina-cosina) de la función periódica .
| Dominio de tiempo | Parcela | Dominio de frecuencia (forma sina-cosina) | Observaciones | Referencia |
|---|---|---|---|---|























![{displaystyle [x_{0},x_{0}+P],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74358f52e616039efc9b1fcc9568f99f6ae93463)
![{displaystyle mathrm {X} _{f}(tau)={tfrac {2}{P}}int _{x_{0}}^{x_{0}+P}s(x)cdot cos left(2pi f(x-tau)right),dx;quad tau in left[0,{tfrac {2pi }{f}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5240eaa70571932d715193314ccebab98f25b305)








![{displaystyle {begin{aligned}mathrm {X} _{n}(varphi)&={tfrac {2}{P}}int _{P}s(x)cdot cos left({tfrac {2pi }{P}}nx-varphi right),dx;quad varphi in [0,2pi ]\&=cos(varphi)cdot underbrace {{tfrac {2}{P}}int _{P}s(x)cdot cos left({tfrac {2pi }{P}}nxright),dx} _{triangleq a_{n}}+sin(varphi)cdot underbrace {{tfrac {2}{P}}int _{P}s(x)cdot sin left({tfrac {2pi }{P}}nxright),dx} _{triangleq b_{n}}\&=cos(varphi)cdot a_{n}+sin(varphi)cdot b_{n}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b65590f785d22d6b81e65752068b5555a7af90a)









![{displaystyle {displaystyle s_{scriptscriptstyle N}(x)={frac {A_{0}}{2}}+sum _{n=1}^{N}left[A_{n}cos(varphi _{n})cdot cos left({tfrac {2pi }{P}}nxright)+A_{n}sin(varphi _{n})cdot sin left({tfrac {2pi }{P}}nxright)right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e904306df1ed48e64053b1f579c8bfab5508157)




![{displaystyle {begin{aligned}cos left({tfrac {2pi }{P}}nx-varphi _{n}right)&{}equiv {tfrac {1}{2}}e^{ileft(2pi nx/P-varphi _{n}right)}+{tfrac {1}{2}}e^{-ileft(2pi nx/P-varphi _{n}right)}\[6pt]&=left({tfrac {1}{2}}e^{-ivarphi _{n}}right)cdot e^{i2pi (+n)x/P}+left({tfrac {1}{2}}e^{-ivarphi _{n}}right)^{*}cdot e^{i2pi (-n)x/P}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ccce1b987630c62705a4a1c8750077d2cd2ade7)




![(-pipi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)



![{displaystyle {begin{aligned}a_{n}&={frac {1}{pi }}int _{-pi }^{pi }s(x)cos(nx),dx=0,quad ngeq 0.\[4pt]b_{n}&={frac {1}{pi }}int _{-pi }^{pi }s(x)sin(nx),dx\[4pt]&=-{frac {2}{pi n}}cos(npi)+{frac {2}{pi ^{2}n^{2}}}sin(npi)\[4pt]&={frac {2,(-1)^{n+1}}{pi n}},quad ngeq 1.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cd645b661c531998472837b4709b23bf2d2c939)

![{displaystyle {begin{aligned}s(x)&={frac {a_{0}}{2}}+sum _{n=1}^{infty }left[a_{n}cos left(nxright)+b_{n}sin left(nxright)right]\[4pt]&={frac {2}{pi }}sum _{n=1}^{infty }{frac {(-1)^{n+1}}{n}}sin(nx),quad mathrm {for} quad x-pi notin 2pi mathbb {Z}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c051045100b8d31eada1c7fcfd414759404ed25b)

![{displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)
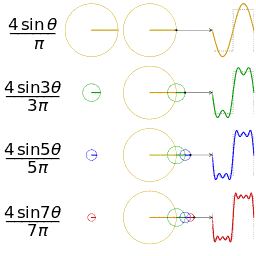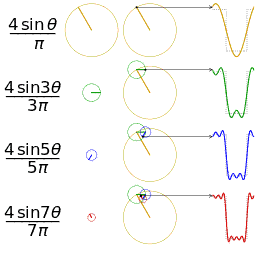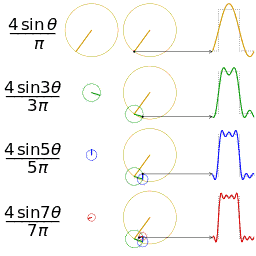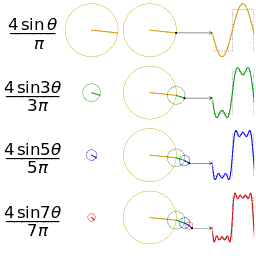










![{displaystyle {begin{aligned}c_{n}&={tfrac {1}{P}}int _{P}operatorname {Re} {s(x)}cdot e^{-i{frac {2pi }{P}}nx} dx+icdot {tfrac {1}{P}}int _{P}operatorname {Im} {s(x)}cdot e^{-i{tfrac {2pi }{P}}nx} dx\[4pt]&={tfrac {1}{P}}int _{P}left(operatorname {Re} {s(x)}+icdot operatorname {Im} {s(x)}right)cdot e^{-i{tfrac {2pi }{P}}nx} dx = {tfrac {1}{P}}int _{P}s(x)cdot e^{-i{tfrac {2pi }{P}}nx} dx.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2f3a7cab08bd95f922c1fbc2f921addb4edfcd3)
![{displaystyle {hat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4759449679108f08a78be5a080c3db89dc27ffea)
![{displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
![{displaystyle {begin{aligned}s_{infty }(x)&=sum _{n=-infty }^{infty }{hat {s}}[n]cdot e^{i,2pi nx/P}\[6pt]&=sum _{n=-infty }^{infty }S[n]cdot e^{i,2pi nx/P}&&scriptstyle {mathsf {common engineering notation}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1a1ac253b5d7a763eff884963eb5efbc5dd0879)
![{displaystyle S(f) triangleq sum _{n=-infty }^{infty }S[n]cdot delta left(f-{frac {n}{P}}right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)


![{displaystyle {begin{aligned}{mathcal {F}}^{-1}{S(f)}&=int _{-infty }^{infty }left(sum _{n=-infty }^{infty }S[n]cdot delta left(f-{frac {n}{P}}right)right)e^{i2pi fx},df,\[6pt]&=sum _{n=-infty }^{infty }S[n]cdot int _{-infty }^{infty }delta left(f-{frac {n}{P}}right)e^{i2pi fx},df,\[6pt]&=sum _{n=-infty }^{infty }S[n]cdot e^{i,2pi nx/P} triangleq s_{infty }(x).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/446316db0d563e8ceac0da5d5d078b67f0c0f4e5)











![{displaystyle (x,y)in [0,pi ]times [0,pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610)











