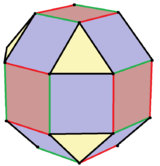
Rombicuboctaedro
| Rhombicuboctahedron | |
|---|---|
 (Haga clic aquí para el modelo giratorio) | |
| Tipo | Arquitecto sólido Uniform polyhedron |
| Elementos | F = 26, E = 48, V = 24 (χ = 2) |
| Caras por lados | 8{3}+(6+12){4} |
| Notación de Conway | eC o aaC aaaa |
| Símbolos de Schläfli | o r{}43}{displaystyle r{begin{Bmatrix}43end{Bmatrix}} |
| t0,2{4,3} | |
| Signatura Wythoff | 3 4 Silencio 2 |
| Coxeter diagrama |     |
| Grupo de Symmetry | Oh, B3, [4,3], (*432), orden 48 |
| Grupo de rotación | O, [4,3]+, (432), orden 24 |
| Ángulo Dihedral | 3-4: 144°44′08′′ (144.74°) 4-4: 135° |
| Referencias | U10, C22, W13 |
| Propiedades | Convex semiregular |
 Caras de colores |  3.4.4.4 (Vertex figure) |
 Deltoidal icositetraedro (poliedro dual) |  Cifras netas |
En geometría, el rombicuboctaedro, o pequeño rombicuboctaedro, es un poliedro con ocho caras triangulares, seis cuadradas y doce rectangulares. Hay 24 vértices idénticos, con un triángulo, un cuadrado y dos rectángulos que se encuentran en cada uno. Si todos los rectángulos son cuadrados (equivalentemente, todos los bordes tienen la misma longitud, asegurando que los triángulos sean equiláteros), es un sólido de Arquímedes. El poliedro tiene simetría octaédrica, como el cubo y el octaedro. Su dual se llama icositetraedro deltoidal o icositetraedro trapezoidal, aunque sus caras no son realmente trapezoides.
Nombres
Johannes Kepler en Harmonices Mundi (1618) llamó a este poliedro rombicuboctaedro, que es la abreviatura de rombo cuboctaédrico truncado, siendo rombo cuboctaédrico su nombre de un dodecaedro rómbico. Hay diferentes truncamientos de un dodecaedro rómbico en un rombicuboctaedro topológico: Destaca su rectificación (izquierda), la que crea el sólido uniforme (centro), y la rectificación del cuboctaedro dual (derecha), que es el núcleo del compuesto dual.
También se le puede llamar cubo u octaedro expandido o cantelado, a partir de operaciones de truncamiento en cualquiera de los poliedros uniformes.
Desde su inclusión en Wings 3D como un "octosapo" este apodo no oficial se está extendiendo.
Relaciones geométricas
Hay distorsiones del rombicuboctaedro que, si bien algunas de las caras no son polígonos regulares, aún tienen vértice uniforme. Algunos de estos se pueden hacer tomando un cubo u octaedro y cortando los bordes, luego recortando las esquinas, de modo que el poliedro resultante tenga seis caras cuadradas y doce rectangulares. Estos tienen simetría octaédrica y forman una serie continua entre el cubo y el octaedro, análoga a las distorsiones del rombicosidodecaedro o las distorsiones tetraédricas del cuboctaedro. Sin embargo, el rombicuboctaedro también tiene un segundo conjunto de distorsiones con seis caras rectangulares y dieciséis trapezoidales, que no tienen simetría octaédrica sino simetría Th, por lo que son invariantes bajo las mismas rotaciones que el tetraedro pero reflexiones diferentes.
Las líneas a lo largo de las cuales se puede girar un cubo de Rubik se proyectan sobre una esfera, similar, topológicamente idéntica, a las aristas de un rombicuboctaedro. De hecho, se han producido variantes que utilizan el mecanismo del cubo de Rubik que se parecen mucho al rombicuboctaedro.
El rombicuboctaedro se usa en tres teselaciones uniformes que llenan el espacio: el panal cúbico cantelado, el panal cúbico truncado y el panal cúbico alternado.
Disección
El rombicuboctaedro se puede dividir en dos cúpulas cuadradas y un prisma octogonal central. Una rotación de una cúpula de 45 grados crea el pseudorrombicuboctaedro. Ambos poliedros tienen la misma figura de vértice: 3.4.4.4.
Hay tres pares de planos paralelos que se cruzan con el rombicuboctaedro en un octágono regular. El rombicuboctaedro se puede dividir a lo largo de cualquiera de estos para obtener un prisma octogonal con caras regulares y dos poliedros adicionales llamados cúpulas cuadradas, que cuentan entre los sólidos de Johnson; es por tanto una ortobicúpula cuadrada alargada. Estas piezas se pueden volver a ensamblar para dar un nuevo sólido llamado girobicúpula cuadrada alargada o pseudorombocuboctaedro, con la simetría de un antiprisma cuadrado. En este los vértices son todos localmente iguales a los de un rombicuboctaedro, con un triángulo y tres cuadrados juntándose en cada uno, pero no todos son idénticos con respecto a todo el poliedro, ya que algunos están más cerca del eje de simetría que otros.
 |  Rhombicuboctahedron |
 Pseudorhombicuboctahedron |
Proyecciones ortogonales
El rombicuboctaedro tiene seis proyecciones ortogonales especiales, centradas, en un vértice, en dos tipos de aristas, y tres tipos de caras: triángulos y dos cuadrados. Los dos últimos corresponden a los planos B2 y A2 de Coxeter.
| Centrado por | Vertex | Edge 3-4 | Edge 4-4 | Cara Plaza-1 | Cara Plaza-2 | Cara Triángulo |
|---|---|---|---|---|---|---|
| Sólido |  |  |  | |||
| Wireframe |  |  |  |  |  |  |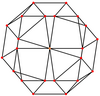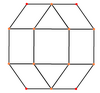
| Projective simetría | [2] | [2] | [2] | [2] | [4] | [6] |
| Doble |  |  |  |  |  |  |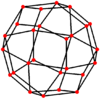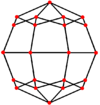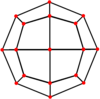
Alicatados esféricos
El rombicuboctaedro también puede representarse como un mosaico esférico y proyectarse en el plano a través de una proyección estereográfica. Esta proyección es conforme, preservando ángulos pero no áreas o longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.
 |  (6) cuadrado centrado |  (6) cuadrado centrado |  (8) triángulo centrado |
| Proyección ortogonal | Proyecciones estereográficas | ||
|---|---|---|---|
Simetría piritoédrica
Una forma media de simetría del rhombicuboctaedro, , existe con simetría piritoedral, [4,3+], (3*2) como diagrama de Coxeter 
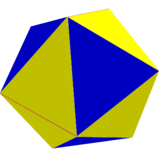
, símbolo Schläfli s2{3,4}, y se puede llamar un cantic snub octahedron. Esta forma se puede visualizar mediante la coloración alterna de los bordes de los 6 cuadrados. Estos cuadrados pueden entonces ser distorsionados en rectángulos, mientras que los 8 triángulos permanecen equiláteros. Las 12 caras cuadradas diagonales se convertirán en isosceles trapezoids. En el límite, los rectángulos se pueden reducir a los bordes, y los trapezoides se convierten en triángulos, y un icosahedro se forma, por un snub octahedron construcción, , s{3,4}. (El compuesto de dos icosahedra se construye a partir de ambas posiciones alternadas.)
| Variaciones de la simetría piritohedral | |||||||||
|---|---|---|---|---|---|---|---|---|---|
 Geometría uniforme |  Geometría no uniforme |  Geometría no uniforme |  En el límite, un icosahedron snub octaedron, ,de una de dos posiciones. |  Compuesto de dos icosahedra de ambas posiciones alternadas. | |||||
Propiedades algebraicas
Coordenadas cartesianas
Las coordenadas cartesianas de los vértices de un rombicuboctaedro centrado en el origen, con arista de longitud 2 unidades, son todas las permutaciones pares de
- (±1, ± 1, ± 1 + √2)).
Si el rombicuboctaedro original tiene una longitud de arista unitaria, su icositetraedro estrombico dual tiene longitudes de arista
- 2710− − 2y4− − 22.{fnMicroc {2} {fnK}}fnuncio {4-2{sqrt {2}}}quad {text{y}}quad {4-2{sqrt {2}}}}}}}}} {f} {fnK} {f}}}} {fnKf}}}} {f}}}}}}}}}}}}}}}}} {f}}}}}}}}}}} {f} {f} {f}}} {f} {f} {f}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}f}} {\f}}}}}f}}}}}}}}}}}}}}}}}f}}}}}}}} {f} {f} {f}}}
Área y volumen
El área A y el volumen V del rombicuboctaedro de longitud de arista a son:
- A=()18+23)a2.. 21.4641016a2V=12+1023a3.. 8.71404521a3.{displaystyle {begin{aligned}A paciente=left(18+2{sqrt {3}right)a^{2} limitándoseapprox 21.464,1016a^{2}V rest={12+10{sqrt {2}}{3}a} {3} {3} {3}} {045,21a^{3}end{aligned}}}}
Densidad de empaquetado compacto
La fracción de empaquetamiento óptima de los rombicuboctaedros viene dada por
- .. =43()42− − 5){displaystyle eta ={tfrac {4}{3}left(4{sqrt {2}-5right)}.
Se notó que este valor óptimo se obtiene en una red de Bravais por de Graaf (2011). Dado que el rombicuboctaedro está contenido en un dodecaedro rómbico cuya esfera inscrita es idéntica a su propia esfera inscrita, el valor de la fracción de empaquetamiento óptima es un corolario de la conjetura de Kepler: se puede lograr colocando un rombicuboctaedro en cada celda del dodecaedro rómbico. nido de abeja, y no se puede superar, ya que en caso contrario se podría superar la densidad óptima de empaquetamiento de esferas poniendo una esfera en cada rombicuboctaedro del hipotético empaquetamiento que lo supera.
En las artes
El Retrato de Luca Pacioli de 1495, tradicionalmente atribuido a Jacopo de' Barbari, incluye un rombicuboctaedro de vidrio medio lleno de agua, que puede haber sido pintado por Leonardo da Vinci. La primera versión impresa del rombicuboctaedro fue de Leonardo y apareció en la Divinaproporcione de Pacioli (1509).
Se puede proyectar una panorámica esférica de 180° × 360° en cualquier poliedro; pero el rombicuboctaedro proporciona una aproximación bastante buena de una esfera y es fácil de construir. Este tipo de proyección, llamada Philosphere, es posible desde algún software de ensamblaje de panoramas. Se compone de dos imágenes que se imprimen por separado y se cortan con tijera dejando unas solapas para el montaje con cola.
Objetos
Los juegos de Freescape Driller y Dark Side tenían un mapa de juego en forma de rombicuboctaedro.
La "Galaxia de prisas y prisas" y "Galaxia del tobogán marino" en el videojuego Super Mario Galaxy tienen planetas en forma similar a un rombicuboctaedro.
La Icecap Zone de Sonic the Hedgehog 3 presenta pilares rematados con rombicuboctaedros.
Durante la moda del cubo de Rubik de la década de 1980, al menos dos rompecabezas retorcidos vendidos tenían la forma de un rombicuboctaedro (el mecanismo era similar al de un cubo de Rubik).
Sundial (1596)
Sundial
Lámpara de calle en Mainz
Muere con 18 caras etiquetadas
El objetivo de disparo de Cabela
La serpiente de Rubik
Variación de Cubo de Rubik
Cristal de pirita
Poliedros relacionados
El rombicuboctaedro es uno de una familia de poliedros uniformes relacionados con el cubo y el octaedro regular.
| Uniform octaedral polyhedra | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Simetría: [4,3], (*432) | [4,3]+ (432) | [1]+,4,3] = [3,3] (*332) | [3]+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31.1} | t{3,4} t{31.1} | {3,4} {3}1.1} | rr{4,3} s2{3,4} | tr{4,3} | sr{4,3} | h{4,3} {3,3} | h2{4,3} t{3,3} | S{3,4} s{31.1} |
| | | | | | | | | ||
 =   | = | =  | |  = o  | = o | =  | ||||
 |  |   |   |   |  |  |  |   |   |   |
| Duals to uniform polyhedra | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
 | | | | | | |  | | | |
| | | | | | | ||||
 |  |  |  |  |  |  |  |  |  |  |
Mutaciones de simetría
Este poliedro está relacionado topológicamente como parte de una secuencia de poliedros cantelados con figura de vértice (3.4.n.4), y continúa como mosaicos del plano hiperbólico. Estas figuras de vértice transitivo tienen (*n32) simetría de reflexión.
| *n32 mutación simetría de los revestimientos ampliados: 3.4.n.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Simmetría *n32 [n,3] | Spherical | Euclid. | Hiperb compacto. | Paracomp. | ||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | |
| Gráfico |  |  | |  |  |  |  |  |
| Config. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4. |
| *n42 mutación simetría de los revestimientos ampliados: n.4.4.4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Simmetría [n,4], (*n42) | Spherical | Euclidean | Hiperbólico compacto | Paracomp. | |||||||
| *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4] | * [∞,4] | |||||
| Ampliación cifras | |  |  |  |  |  |  | ||||
| Config. | 3.4.4.4 | 4.4.4 | 5.4.4 | 6.4.4.4 | 7.4.4.4 | 8.4.4 | ∞.4.4 | ||||
| Rhombic cifras Config. |  V3.4.4.4 |  V4.4.4.4 |  V5.4.4.4 |  V6.4.4.4 |  V7.4.4.4 |  V8.4.4.4 |  V∞.4.4.4 | ||||
Disposición de vértices
Comparte su disposición de vértices con tres poliedros uniformes no convexos: el hexaedro truncado estrellado, el rombihexaedro pequeño (que tiene las caras triangulares y seis caras cuadradas en común) y el cuboctaedro cúbico pequeño (que tiene doce caras cuadradas en común).
Rhombicuboctahedron |  Pequeño cuboctaedro |  Pequeño rhombihexahedron |  Hexahedron truncado estelar |
Gráfico de rombicuboctaedro
El grafo rombicuboctaédrico es el gráfico de vértices y aristas del rombicuboctaedro. Tiene 24 vértices y 48 aristas, y es un grafo de Arquímedes cuartico.
Contenido relacionado
Hiperplano
Isotropía
Cuboctaedro