Cuboctaedro

Cuboctahedron
(Haga clic aquí para el modelo giratorio)
Tipo	Arquitecto sólido Uniform polyhedron
Elementos	F = 14, E = 24, V = 12 (χ = 2)
Caras por lados	8{3}+6{4}
Notación de Conway	aC aaT
Símbolos de Schläfli	o {}43}{displaystyle {begin{Bmatrix}43end{Bmatrix}} o r{}33}{displaystyle r{begin{Bmatrix}33end{Bmatrix}}
	t1{4,3} o t0,2{3,3}
Signatura Wythoff	2 Silencio 3 4 3 3 Silencio 2
Coxeter diagrama	o o
Grupo de Symmetry	Oh, B3, [4,3], (*432), orden 48 Td, [3,3], (*332), orden 24
Grupo de rotación	O, [4,3]+, (432), orden 24
Ángulo Dihedral	125,26° arcsec(−√3)
Referencias	U07, C19, W11
Propiedades	Semiregular convex quasiregular
Caras de colores	3.4.3.4 (Vertex figure)
Rhombic dodecahedron (poliedro dual)	Cifras netas

Modelo 3D de un cuboctaedro

Un cuboctaedro es un poliedro de 8 caras triangulares y 6 caras cuadradas. Un cuboctaedro tiene 12 vértices idénticos, con 2 triángulos y 2 cuadrados que se encuentran en cada uno, y 24 aristas idénticas, cada una de las cuales separa un triángulo de un cuadrado. Como tal, es un poliedro cuasiregular, es decir, un sólido de Arquímedes que no solo es transitivo de vértice sino también transitivo de borde. Es radialmente equilátero.

Su poliedro dual es el dodecaedro rómbico.

El cuboctaedro probablemente era conocido por Platón: las Definiciones de Heron citan a Arquímedes diciendo que Platón conocía un sólido formado por 8 triángulos y 6 cuadrados.

Sinónimos

• Vector Equilibrium (Buckminster Fuller) porque su radio centro-a-vertex equivale a su longitud de borde (tiene simetría equilateral radial). Fuller también llamado cuboctaedro construido de struts rígidos y vértices flexibles a jitterbug; este objeto se puede transformar progresivamente en un icosahedro, octaedro y tetraedro doblando a lo largo de las diagonales de sus lados cuadrados.
• Con O_h simetría, orden 48, es una cubo rectificado o octaedro rectificado (Norman Johnson)
• Con T_d simetría, orden 24, es una tetraedro o rhombitetratetrahedron.
• Con D_3d simetría, orden 12, es una gyrobicupola triangular.

Proyecciones ortogonales

El cuboctaedro tiene cuatro proyecciones ortogonales especiales, centradas en un vértice, una arista y los dos tipos de caras, triangular y cuadrada. Los dos últimos corresponden a los planos B₂ y A₂ de Coxeter. Las proyecciones oblicuas muestran un cuadrado y un hexágono que pasan por el centro del cuboctaedro.

Cuboctahedron (proyecciones ortogonales)

Plaza Cara	Triangular Cara	Vertex	Edge	Skew
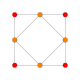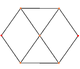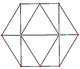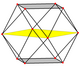[4]	[6]	[2]	[2]
Rhombic dodecahedron (Dual polyhedron)

Alicatados esféricos

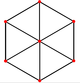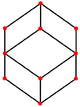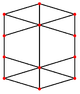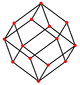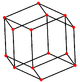El cuboctaedro también se puede representar como un mosaico esférico y proyectarse en el plano a través de una proyección estereográfica. Esta proyección es conforme, preservando ángulos pero no áreas o longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.

proyección ortográfico	cuadrado centrado	triángulo centrado	Vertex centrado
	Proyección estereográfica

Estructura

Coordenadas

Las coordenadas cartesianas de los vértices de un cuboctaedro (de longitud de arista √2 ) centrados en el origen son:

(±1,±1,0)

(±1,0,±1)

(0,±1,±1)

Se puede crear un conjunto alternativo de coordenadas en 4 espacios, como 12 permutaciones de:

(0,1,1,2)

Esta construcción existe como una de las 16 facetas ortantes de las 16 celdas canteladas.

Vectores raíz

Los 12 vértices del cuboctaedro pueden representar los vectores raíces del grupo de Lie simple A₃. Con la adición de 6 vértices del octaedro, estos vértices representan los 18 vectores raíz del grupo de Lie simple B₃.

Propiedades métricas

El área A y el volumen V del cuboctaedro de longitud de arista a son:

A=()6+23)a2.. 9.4641016a2V=532a3.. 2.3570226a3.{displaystyle {begin{aligned}A paciente=left(6+2{sqrt {3}right)a^{2} limiteapprox 9.464,1016a^{2}V diez={tfrac {5}{3} {2}a} {3} 2.357,0226a^{3}

Disección

Tetraedros y Octaedros

El cuboctaedro se puede dividir en 6 pirámides cuadradas y 8 tetraedros que se encuentran en un punto central. Esta disección se expresa en el panal tetraédrico-octaédrico donde los pares de pirámides cuadradas se combinan en octaedros.

Poliedros irregulares

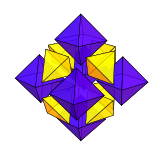
El cuboctaedro se puede dividir en dos cúpulas triangulares mediante un hexágono común que pasa por el centro del cuboctaedro. Si estas dos cúpulas triangulares se tuercen de modo que los triángulos y los cuadrados se alineen, se crea el sólido Johnson J₂₇, la ortobicúpula triangular.

Relaciones geométricas

Progresión entre un tetraedro, expandido en un cuboctaedro, y reverso expandido en el doble tetraedro

Simetría equilátera radial

En un cuboctaedro, el radio mayor (del centro al vértice) es igual a la longitud de la arista; por lo tanto, su diámetro largo (vértice al vértice opuesto) es 2 longitudes de borde. Su centro es como el vértice apical de una pirámide: un borde alejado de todos los otros vértices. (En el caso del cuboctaedro, el centro es de hecho el vértice de 6 pirámides cuadradas y 8 triangulares). Esta simetría equilátera radial es una propiedad de solo unos pocos politopos uniformes, incluido el hexágono bidimensional, el cuboctaedro tridimensional y el teseracto de cuatro dimensiones de 24 celdas y 8 celdas. Los politopos radialmente equiláteros son aquellos que pueden construirse, con sus radios largos, a partir de triángulos equiláteros que se encuentran en el centro del politopo, aportando cada uno dos radios y una arista. Por lo tanto, todos los elementos interiores que se encuentran en el centro de estos politopos tienen caras internas de triángulos equiláteros, como en la disección del cuboctaedro en 6 pirámides cuadradas y 8 tetraedros.

Cada uno de estos politopos radialmente equiláteros también se presenta como células de una característica teselación que llena el espacio: el mosaico de hexágonos regulares, el panal cúbico rectificado (de cuboctaedros y octaedros alternados), el panal de 24 celdas y el panal teseractico, respectivamente. Cada mosaico tiene un mosaico dual; los centros de celda en una teselación son vértices de celda en su teselación dual. El empaque de esfera regular más denso conocido en dos, tres y cuatro dimensiones utiliza los centros de las celdas de una de estas teselaciones como centros de esfera.

Un cuboctaedro tiene simetría octaédrica. Su primera estelación es el compuesto de un cubo y su octaedro dual, con los vértices del cuboctaedro ubicados en los puntos medios de los bordes de cualquiera.

Construcciones

Se puede obtener un cuboctaedro tomando una sección transversal ecuatorial de una celda tetradimensional de 24 o 16 celdas. Se puede obtener un hexágono o un cuadrado tomando una sección transversal ecuatorial de un cuboctaedro.

El cuboctaedro es un cubo rectificado y también un octaedro rectificado.

También es un tetraedro cantellado. Con esta construcción se da el símbolo Wythoff: 3 3 Silencio 2.

Una cantelación oblicua del tetraedro produce un sólido con caras paralelas a las del cuboctaedro, es decir, ocho triángulos de dos tamaños y seis rectángulos. Si bien sus bordes son desiguales, este sólido permanece vertex-uniforme: el sólido tiene el grupo de simetría tetraédrica completa y sus vértices son equivalentes en ese grupo.

Las aristas de un cuboctaedro forman cuatro hexágonos regulares. Si el cuboctaedro se corta en el plano de uno de estos hexágonos, cada mitad es una cúpula triangular, uno de los sólidos de Johnson; el propio cuboctaedro, por lo tanto, también puede llamarse girobicúpula triangular, el más simple de una serie (aparte del girobifastigium o "girobicúpula digonal"). Si las mitades se vuelven a juntar con un giro, de modo que los triángulos se unan a los triángulos y los cuadrados se unan a los cuadrados, el resultado es otro sólido de Johnson, la ortobicúpula triangular, también llamada anticuboctaedro.

Ambas bicúpulas triangulares son importantes en el empaquetamiento de esferas. La distancia desde el centro del sólido hasta sus vértices es igual a la longitud de su borde. Cada esfera central puede tener hasta doce vecinos, y en una red cúbica centrada en las caras, estos toman las posiciones de los vértices de un cuboctaedro. En una red hexagonal compacta, corresponden a las esquinas de la ortobicúpula triangular. En ambos casos la esfera central toma la posición del centro del sólido.

Los cuboctaedros aparecen como células en tres de los panales uniformes convexos y en nueve de los 4 politopos uniformes convexos.

El volumen del cuboctaedro es 5/6 del cubo que lo encierra y 5/8 del octaedro envolvente.

Disposición de vértices

Debido a que es radialmente equilátero, el centro del cuboctaedro se puede tratar como un 13.° vértice apical canónico, una longitud de borde distante de los 12 vértices ordinarios, como el vértice de una pirámide canónica. es la longitud de una arista equidistante de sus otros vértices.

El cuboctaedro comparte sus aristas y disposición de vértices con dos poliedros uniformes no convexos: el cubohemioctaedro (que tiene las caras cuadradas en común) y el octahemioctaedro (que tiene las caras triangulares en común), ambos tienen cuatro hexágonos. También sirve como tetraedro cantelado, como un tetratetraedro rectificado.

Cuboctahedron

su Ecuador

Cubohemioctaedron

Octahemioctaedron

El cuboctaedro 2-cubre el tetrahemihexaedro, que en consecuencia tiene la misma figura de vértice abstracto (dos triángulos y dos cuadrados: 3.4.3.4) y la mitad de vértices, aristas y caras. (La figura real del vértice del tetrahemihexaedro es 3.4.3/2.4, con un/2 factor debido al cruce).

Cuboctahedron

Tetrahemihexahedron

Cinemática

Progresiones entre un octaedro, pseudoicosaedro y cuboctaedro. El cuboctaedro puede flexionar de esta manera incluso si sus bordes (pero no sus caras) son rígidos.

Cuando se interpreta como un marco de caras planas rígidas, conectadas a lo largo de los bordes por bisagras, el cuboctaedro es una estructura rígida, como lo son todos los poliedros convexos, según el teorema de Cauchy. Sin embargo, cuando se eliminan las caras, dejando solo bordes rígidos conectados por juntas flexibles en los vértices, el resultado no es un sistema rígido. (a diferencia de los poliedros cuyas caras son todos triángulos, a los que se aplica el teorema de Cauchy a pesar de las caras que faltan).

Al agregar un vértice central, conectado por aristas rígidas a todos los demás vértices, se subdivide el cuboctaedro en pirámides cuadradas y tetraedros, que se unen en el vértice central. A diferencia del propio cuboctaedro, el sistema resultante de aristas y uniones es rígido y forma parte de la estructura de celosía de octetos infinitos.

Polítopos relacionados

Poliedros regulares

El cuboctaedro es uno de una familia de poliedros uniformes relacionados con el cubo y el octaedro regular.

Uniform octaedral polyhedra
Simetría: [4,3], (*432)							[4,3]+ (432)	[1]+,4,3] = [3,3] (*332)		[3]+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31.1}	t{3,4} t{31.1}	{3,4} {3}1.1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	S{3,4} s{31.1}
		=	=	=				= o	= o	=
Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

El cuboctaedro también tiene simetría tetraédrica con dos colores de triángulos.

Familia de polihedra de tetraedral uniforme
Simetría: [3,3], (*332)							[3,3]+, (332)
{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duals to uniform polyhedra
V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3

Poliedros cuasiregulares y mosaicos

El cuboctaedro existe en una secuencia de simetrías de poliedros cuasiregulares y mosaicos con configuraciones de vértice (3.n)², progresando desde mosaicos de la esfera hasta el plano euclidiano y en el plano hiperbólico. Con la simetría de notación orbifold de *n32, todas estas teselaciones son construcciones Wythoff dentro de un dominio fundamental de simetría, con puntos generadores en la esquina del ángulo derecho del dominio.

* n32 simetrías orbifold de baldosas cuasiregulares: (3.n)2
Construcción	Spherical			Euclidean	Hiperbólico
	*332	*432	*532	*632	*732	*832...	*∞32
Quasiregular cifras
Vertex	(3.3)2	(3.4)2	(3.5)2	(3.6)2	(3.7)2	(3.8)2	(3.

*n42 mutaciones de simetría de los revestimientos cuasiregulares: (4.n)2 v t e
Simmetría *4n2 [n,4]	Spherical	Euclidean	Hiperbólico compacto				Paracompactar	No
	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	* [∞,4]	[ni,4]
Gráficos
Config.	(4.3)2	(4.4)2	(4.5)2	(4.6)2	(4.7)2	(4.8)2	(4.	(4.ni)2

Este poliedro está relacionado topológicamente como parte de una secuencia de poliedros cantelados con figura de vértice (3.4.n.4), y continúa como mosaicos del plano hiperbólico. Estas figuras de vértice transitivo tienen (*n32) simetría de reflexión.

*n32 mutación simetría de los revestimientos ampliados: 3.4.n.4
Simmetría *n32 [n,3]	Spherical				Euclid.	Hiperb compacto.		Paracomp.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Gráfico
Config.	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.4	3.4.8.4	3.4.

Politopos de 4 dimensiones

Proyecciones ortogonales de 24 celdas

El cuboctaedro se puede descomponer en un octaedro regular y ocho octaedros irregulares pero iguales en la forma del casco convexo de un cubo con dos vértices opuestos eliminados. Esta descomposición del cuboctaedro se corresponde con la primera proyección paralela de celda de las 24 celdas en tres dimensiones. Bajo esta proyección, el cuboctaedro forma la envolvente de proyección, que se puede descomponer en seis caras cuadradas, un octaedro regular y ocho octaedros irregulares. Estos elementos se corresponden con las imágenes de seis de las celdas octaédricas en las 24 celdas, las celdas más cercanas y más lejanas desde el punto de vista 4D y los ocho pares de celdas restantes, respectivamente.

Gráfico cuboctaédrico

En el campo matemático de la teoría de grafos, un grafo cuboctaédrico es el gráfico de vértices y aristas del cuboctaedro, uno de los sólidos de Arquímedes. También se puede construir como el gráfico lineal del cubo. Tiene 12 vértices y 24 aristas, es localmente lineal y es un grafo de Arquímedes cuartico.

proyección ortogonal

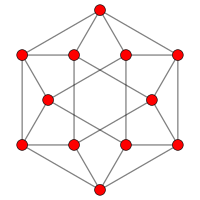Simetría de 6 veces