Relación transitiva (matemáticas)

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

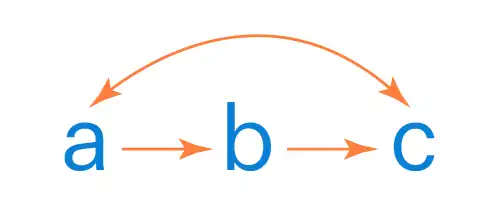
Ejemplificación de la relación transitiva — Si a se relaciona con b y b con c, entonces a con c

Una relación transitiva es un tipo de relación binaria formada cuando un elemento se relaciona con un segundo elemento y este con un tercer elemento, por lo que se crea una relación entre el primero y el tercero.

Matemáticamente, una relación binaria R en un conjunto X se define como transitiva cuando cumple una condición específica: si para cualquier trío de elementos a, b, c pertenecientes a X, se da que R relaciona a con b y a su vez b se relaciona con c, entonces R también relaciona directamente a con c.

Este tipo de relación es un pilar en diversas estructuras matemáticas. Por ejemplo, tanto los órdenes parciales como las relaciones de equivalencia son ejemplos clásicos de relaciones transitivas. Estas estructuras son esenciales para entender la organización y jerarquía dentro de los conjuntos matemáticos.

Un caso ilustrativo de la relación transitiva se observa en las operaciones de desigualdad e igualdad entre números reales. Tomemos, por ejemplo, una desigualdad: si tenemos que a < b y b < c, entonces, siguiendo la propiedad transitiva, se deduce que a < c. De manera similar, en el caso de la igualdad, si x = m y m = z, entonces necesariamente x = z. La transitividad ayuda a establecer conexiones lógicas y coherentes entre diferentes elementos de un conjunto.

HSD

Definición

Una relación homogénea R sobre el conjunto X es una relación transitiva si,para todo a, b, c ∈ X, si a R b y b R c, entonces a R c.

O en términos de lógica de primer orden: $para todo a,b,cen X:(aRbcuña bRc)Rightarrow aRc$ ,

donde a R b es la notación infija para (a, b) ∈ R.

Ejemplos

Como ejemplo no matemático, la relación "es un antepasado de" es transitiva. Por ejemplo, si Amy es antepasada de Becky y Becky es antepasada de Carrie, Amy también es antepasada de Carrie.

Por otro lado, "es la madre biológica de" no es una relación transitiva, porque si Alice es la madre biológica de Brenda y Brenda es la madre biológica de Claire, entonces Alice no es la madre biológica de Claire. Es más, es antitransitivo: Alice nunca puede ser la madre biológica de Claire.

"Es mayor que", "es al menos tan grande como" y "es igual a" (igualdad) son relaciones transitivas en varios conjuntos, por ejemplo, el conjunto de números reales o el conjunto de números naturales:siempre que x > y y y > z, entonces también x > zsiempre que x ≥ y y y ≥ z, entonces también x ≥ zsiempre que x = y y y = z, entonces también x = z.

Más ejemplos de relaciones transitivas:

"es un subconjunto de" (inclusión de conjuntos, una relación en conjuntos)
"divide" (divisibilidad, una relación de números naturales)
"implica" (implicación, simbolizada por "⇒", una relación sobre proposiciones)

Ejemplos de relaciones no transitivas:

"es el sucesor de" (una relación sobre números naturales)
"es un miembro del conjunto" (simbolizado como "∈")
"es perpendicular a" (una relación sobre líneas en geometría euclidiana)

La relación vacía en cualquier conjunto $X$ es transitiva porque no hay elementos ${ estilo de visualización a, b, c en X}$ tales que ${displaystyle aRb}$ y ${displaystyle bRc}$ , y por lo tanto la condición de transitividad es vacíamente verdadera. Una relación R que contiene solo un par ordenado también es transitiva: si el par ordenado es de la forma $(x,x)$ para algunos $xen X$ , los únicos elementos de este tipo ${ estilo de visualización a, b, c en X}$ son ${ estilo de visualización a = b = c = x}$ , y de hecho en este caso ${displaystyle arco}$ , mientras que si el par ordenado no es de la forma $(x,x)$ , entonces no existen tales elementos. ${ estilo de visualización a, b, c en X}$ y por tanto $R$ es vacuamente transitiva.

Propiedades

Propiedades de cierre

El converso (inverso) de una relación transitiva es siempre transitiva. Por ejemplo, sabiendo que "es un subconjunto de" es transitivo y "es un superconjunto de" es su recíproco, se puede concluir que este último también es transitivo.
La intersección de dos relaciones transitivas es siempre transitiva. Por ejemplo, sabiendo que "nació antes" y "tiene el mismo nombre que" son transitivos, se puede concluir que "nació antes y también tiene el mismo nombre que" también es transitivo.
La unión de dos relaciones transitivas no necesita ser transitiva. Por ejemplo, "nació antes o tiene el mismo nombre que" no es una relación transitiva, ya que, por ejemplo, Herbert Hoover está relacionado con Franklin D. Roosevelt, que a su vez está relacionado con Franklin Pierce, mientras que Hoover no está relacionado con Franklin Pierce..
El complemento de una relación transitiva no necesita ser transitivo. Por ejemplo, mientras que "igual a" es transitivo, "no igual a" solo es transitivo en conjuntos que tienen como máximo un elemento.

Otras propiedades

Una relación transitiva es asimétrica si y sólo si es irreflexiva.

Una relación transitiva no necesita ser reflexiva. Cuando lo es, se llama preorden. Por ejemplo, en el conjunto X = {1,2,3}:

R = { (1,1), (2,2), (3,3), (1,3), (3,2) } es reflexivo, pero no transitivo, ya que el par (1,2) está ausente,
R = {(1,1), (2,2), (3,3), (1,3) } es tanto reflexivo como transitivo, por lo que es un preorden,
R = {(1,1), (2,2), (3,3) } es tanto reflexivo como transitivo, otro preorden.

Extensiones transitivas y cierre transitivo

Sea R una relación binaria en el conjunto X. La extensión transitiva de R, denotada por R ₁, es la relación binaria más pequeña en X tal que R ₁ contiene R, y si (a, b) ∈ R y (b, c) ∈ R entonces (a, c) ∈ R ₁. Por ejemplo, supongamos que X es un conjunto de pueblos, algunos de los cuales están conectados por carreteras. DejarSea R la relación de los pueblos donde (A, B) ∈ R si hay una carretera que une directamente el pueblo A y el pueblo B. Esta relación no necesita ser transitiva. La extensión transitiva de esta relación se puede definir por (A, C) ∈ R ₁ si se puede viajar entre los pueblos A y C utilizando como máximo dos caminos.

Si una relación es transitiva entonces su extensión transitiva es ella misma, es decir, si R es una relación transitiva entonces R ₁ = R.

La extensión transitiva de R ₁ se denotaría por R ₂, y siguiendo así, en general, la extensión transitiva de R _i sería R _{i + 1}. La clausura transitiva de R, denotada por R * o R es la unión de conjuntos de R, R ₁, R ₂,....

La clausura transitiva de una relación es una relación transitiva.

La relación "es el padre biológico de" sobre un conjunto de personas no es una relación transitiva. Sin embargo, en biología a menudo surge la necesidad de considerar la paternidad biológica sobre un número arbitrario de generaciones: la relación "es un antepasado biológico de" es una relación transitiva y es el cierre transitivo de la relación "es el padre biológico de".

Para el ejemplo de pueblos y carreteras anterior, (A, C) ∈ R * siempre que pueda viajar entre los pueblos A y C utilizando cualquier cantidad de caminos.

Propiedades de relación que requieren transitividad

Preorder – una relación reflexiva y transitiva
Orden parcial: un preorden antisimétrico
Pedido anticipado total: un pedido anticipado conectado (anteriormente llamado total)
Relación de equivalencia: un preorden simétrico
Ordenamiento débil estricto: un orden parcial estricto en el que la incomparabilidad es una relación de equivalencia
Ordenamiento total: una relación conectada (total), antisimétrica y transitiva

Contando relaciones transitivas

No se conoce ninguna fórmula general que cuente el número de relaciones transitivas en un conjunto finito (secuencia A006905 en la OEIS). Sin embargo, existe una fórmula para encontrar el número de relaciones que son simultáneamente reflexivas, simétricas y transitivas, es decir, relaciones de equivalencia (secuencia A000110 en la OEIS), las que son simétricas y transitivas, las que son simétricas, transitivas, y antisimétricos, y los que son totales, transitivos y antisimétricos. Pfeiffer ha hecho algunos progresos en esta dirección, expresando las relaciones con combinaciones de estas propiedades en términos de cada uno, pero todavía es difícil calcular cualquiera. Véase también Brinkmann y McKay (2005).Mala demostró que ningún polinomio con coeficientes enteros puede representar una fórmula para el número de relaciones transitivas en un conjunto y encontró ciertas relaciones recursivas que proporcionan límites inferiores para ese número. También demostró que ese número es un polinomio de grado dos si el conjunto contiene exactamente dos pares ordenados.

{estilo de texto sum _{k=0}^{n}k!S(n,k)}

Elementos	Ningún	Transitivo	Reflexivo	Simétrico	Hacer un pedido	Orden parcial	Reserva total	Orden total	Relación de equivalencia
0	1	1	1	1	1	1	1	1	1
1	2	2	1	2	1	1	1	1	1
2	dieciséis	13	4	8	4	3	3	2	2
3	512	171	64	64	29	19	13	6	5
4	65,536	3,994	4,096	1,024	355	219	75	24	15
norte	2		2	2			${estilo de texto sum _{k=0}^{n}k!S(n,k)}$	n !	${estilo de texto sum _{k=0}^{n}S(n,k)}$
OEIS	A002416	A006905	A053763	A006125	A000798	A001035	A000670	A000142	A000110

Tenga en cuenta que S (n, k) se refiere a los números de Stirling del segundo tipo.

Propiedades relacionadas

Una relación R se llama intransitiva si no es transitiva, es decir, si xRy y yRz, pero no xRz, para alguna x, y, z. En contraste, una relación R se llama antitransitiva si xRy e yRz siempre implican que xRz no se cumple. Por ejemplo, la relación definida por xRy si xy es un número par es intransitiva, pero no antitransitiva. La relación definida por xRy si x es par yy es impar es tanto transitivo como antitransitivo. La relación definida por xRy si x es el número sucesor de y es tanto intransitiva como antitransitiva. Surgen ejemplos inesperados de intransitividad en situaciones tales como cuestiones políticas o preferencias de grupo.

Generalizado a versiones estocásticas (transitividad estocástica), el estudio de la transitividad encuentra aplicaciones en la teoría de la decisión, la psicometría y los modelos de utilidad.

Una relación cuasitransitiva es otra generalización; se requiere que sea transitivo solo en su parte no simétrica. Tales relaciones se utilizan en la teoría de la elección social o en la microeconomía.

Proposición: Si R es univalente, entonces R;R es transitivo.prueba: Supongamos ${displaystyle xR;R^{T}yR;R^{T}z.}$ que entonces hay ayb tales que Como R es univalente, yRb y aR y implican a = b . Por lo tanto x R a R z de modo que x R;R z y R;R es transitivo. ${displaystyle xRaR^{T}yRbR^{T}z.}$

Corolario: si R es univalente, entonces R;R es una relación de equivalencia en el dominio de R.prueba: R;R es simétrico y reflexivo en su dominio. Con la univalencia de R, se cumple el requisito transitivo de equivalencia.

Contenido relacionado

Más resultados...