Relación antisimétrica

Relaciones binarias transitivas
Simétrico Antisymmetric Conectado Bien fundada Has joineds Has meets Reflexivo Irreflexivo Asimétrica Total, Semiconnex Anti- reflexivo Equivalencia relación Y ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Preorden (Quasiorder) ✗ ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Orden parcial ✗ Y ✗ ✗ ✗ ✗ Y ✗ ✗ Total preordenado ✗ ✗ Y ✗ ✗ ✗ Y ✗ ✗ Orden total ✗ Y Y ✗ ✗ ✗ Y ✗ ✗ Prewellordering ✗ ✗ Y Y ✗ ✗ Y ✗ ✗ Bien ordenado ✗ ✗ ✗ Y ✗ ✗ Y ✗ ✗ Bien ordenado ✗ Y Y Y ✗ ✗ Y ✗ ✗ Lattice ✗ Y ✗ ✗ Y Y Y ✗ ✗ Join-semilattice ✗ Y ✗ ✗ Y ✗ Y ✗ ✗ Meet-semilattice ✗ Y ✗ ✗ ✗ Y Y ✗ ✗ Orden parcial estricta ✗ ✗ ✗ ✗ ✗ ✗ ✗ Y Y Orden débil estricto ✗ ✗ ✗ ✗ ✗ ✗ ✗ Y Y Orden total estricta ✗ ✗ Y ✗ ✗ ✗ ✗ Y Y Simétrico Antisymmetric Conectado Bien fundada Has joineds Has meets Reflexivo Irreflexivo Asimétrica Definiciones, para todos ${displaystyle a,b}$ y ${displaystyle Sneq varnothing:}$ ${displaystyle {begin{aligned}ducaRb\\\\\\\\\\\\\\\\\\\}}}}}$ ${displaystyle {begin{aligned}aRb{text{ and } {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn}}}}}}}}$ ${displaystyle {begin{aligned}aneq {} {fn}} {fn} {fn}} {fn}} {fn}}}} {fn}}}}}} {fn}}}}$ ${displaystyle {begin{aligned}min} S\{text{exists}end{aligned}}$ ${displaystyle {begin{aligned}avee b{text{exists}end{aligned}}}$ ${displaystyle {begin{aligned}awedge b\{text{exists}end{aligned}}}$ ${displaystyle aRa}$ ${displaystyle {text{not }a Ra.$ ${displaystyle {begin{aligned}aRb Rightarrow Raend{aligned}}$
Y indica que la propiedad de la columna es requerida por la definición del término de la fila (a la izquierda). Por ejemplo, la definición de una relación de equivalencia requiere que sea simétrica. ✗ indica que la propiedad puede, o no puede retener. Todas las definiciones requieren tácitamente la relación homogénea ${displaystyle R.$ ser transitivo: para todos ${displaystyle a,b,c,}$ si ${displaystyle ARb!$ y ${displaystyle bRc}$ entonces ${displaystyle ARc,}$ y hay propiedades adicionales que una relación homogénea puede satisfacer.

En matemáticas, una relación binaria ${displaystyle R.$ en un set ${displaystyle X}$ es antisimétrico si no hay par de diferencia elementos ${displaystyle X}$ cada uno de los cuales está relacionado ${displaystyle R.$ al otro. Más formalmente, ${displaystyle R.$ es antisimétrico precisamente si ${displaystyle a,bin X,}$

$${displaystyle {text{if},aRb,{text{ with },aneq b,{text{ then },bRa,{text{ must not hold}}}$$

$${displaystyle {text{if},aRb,{text{ and },bRa,{text{ then },a=b}$$

${displaystyle aRa}$

${displaystyle a}$

${displaystyle R.$

${displaystyle X}$

${displaystyle aRa}$

${displaystyle ain X}$

${displaystyle aRa}$

${displaystyle ain X}$

Ejemplos

La relación de divisibilidad sobre los números naturales es un ejemplo importante de una relación antisimétrica. En este contexto, la antisimetría significa que la única manera de que cada uno de dos números pueda ser divisible por el otro es si los dos son, de hecho, el mismo número; equivalente, si ${displaystyle n}$ y ${displaystyle m}$ son distintos ${displaystyle n}$ es un factor ${displaystyle m,}$ entonces ${displaystyle m}$ no puede ser un factor ${displaystyle n.}$ Por ejemplo, 12 es divisible por 4, pero 4 no es divisible por 12.

La relación de orden habitual ${displaystyle ,leq ,}$ en los números reales es antisimétrico: si para dos números reales ${displaystyle x}$ y ${displaystyle y}$ ambas desigualdades ${displaystyle xleq y}$ y ${displaystyle yleq x}$ Espera, entonces ${displaystyle x}$ y ${displaystyle y}$ Debe ser igual. Análogamente, el orden del subconjunto ${displaystyle ,subseteq ,}$ en los subconjuntos de cualquier conjunto dado es antisimétrico: dado dos conjuntos ${displaystyle A}$ y ${displaystyle B,}$ si cada elemento en ${displaystyle A}$ también está en ${displaystyle B}$ y cada elemento en ${displaystyle B}$ también está ${displaystyle A,}$ entonces ${displaystyle A}$ y ${displaystyle B}$ debe contener todos los mismos elementos y por lo tanto ser igual:

$${displaystyle Asubseteq B{text{ and }Bsubseteq A{text{ implies }A=B}$$

Propiedades

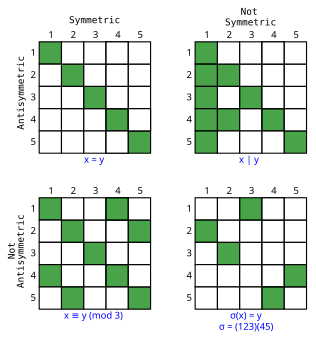
Relaciones simétricas y antisimétricas

Los pedidos parciales y totales son antisimétricos por definición. Una relación puede ser tanto simétrica como antisimétrica (en este caso, debe ser correflexiva), y hay relaciones que no son ni simétricas ni antisimétricas (por ejemplo, la relación "presas de" sobre especies biológicas).

La antisimetría es diferente de la asimetría: una relación es asimétrica si y solo si es antisimétrica e irreflexiva.