Regla de cálculo

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Computación analógica mecánica

Una típica regla de diapositivas de estudiantes de 10 pulgadas (25 cm) (Pickett N902-T simplex trig), también conocido coloquialmente en los Estados Unidos como un palillo

La regla de cálculo es una computadora analógica mecánica que se utiliza principalmente para la multiplicación y la división, y para funciones como exponentes, raíces, logaritmos y trigonometría. Por lo general, no está diseñado para sumar o restar, que generalmente se realiza utilizando otros métodos. La precisión máxima para las reglas de cálculo lineales estándar es de aproximadamente tres dígitos significativos decimales, mientras que la notación científica se utiliza para realizar un seguimiento del orden de magnitud de los resultados.

Las reglas de cálculo existen en una amplia gama de estilos y generalmente aparecen en forma lineal, circular o cilíndrica, con escalas de reglas de cálculo inscritas con marcas graduadas estandarizadas. Las reglas de cálculo fabricadas para campos especializados como la aviación o las finanzas suelen presentar escalas adicionales que ayudan en los cálculos especializados particulares de esos campos. La regla de cálculo está estrechamente relacionada con los nomogramas utilizados para cálculos específicos de aplicaciones. Aunque es similar en nombre y apariencia a una regla estándar, la regla de cálculo no está diseñada para medir longitudes o dibujar líneas rectas.

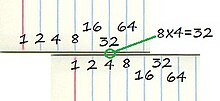
En su forma más simple, cada número que se va a multiplicar está representado por una longitud en un par de reglas paralelas que se pueden deslizar una al lado de la otra. Como las reglas tienen cada una una escala logarítmica, es posible alinearlas para leer la suma de los números' logaritmos, y por lo tanto calcular el producto de los dos números.

El matemático y clérigo inglés Reverendo William Oughtred y otros desarrollaron la regla de cálculo en el siglo XVII basándose en el trabajo emergente sobre logaritmos de John Napier. Antes de la llegada de la calculadora electrónica, era la herramienta de cálculo más utilizada en ciencia e ingeniería. La facilidad de uso, la disponibilidad inmediata y el bajo costo de la regla de cálculo hicieron que su uso siguiera creciendo durante las décadas de 1950 y 1960, incluso cuando las computadoras electrónicas se introducían gradualmente. La introducción de la calculadora científica electrónica portátil alrededor de 1974 hizo que las reglas de cálculo quedaran obsoletas y la mayoría de los proveedores abandonaron el negocio.

Conceptos básicos

Cursor en una regla de diapositivas

En su forma más básica, la regla de cálculo utiliza dos escalas logarítmicas para realizar multiplicaciones y divisiones rápidas de números. Estas operaciones comunes pueden llevar mucho tiempo y ser propensas a errores cuando se realizan en papel. Las reglas de cálculo más elaboradas pueden realizar otros cálculos, como raíces cuadradas, exponenciales, logaritmos y funciones trigonométricas.

Las escalas se pueden agrupar en décadas, que son números que van del 1 al 10 (es decir, 10ⁿ a 10^{n+ 1}). Por lo tanto, las escalas C y D de una sola década van de 1 a 10 en toda la longitud de la regla de cálculo, mientras que las escalas A y B de dos décadas van de 1 a 100 en toda la longitud de la regla de cálculo.

En general, los cálculos matemáticos se realizan alineando una marca en la tira central deslizante con una marca en una de las tiras fijas y luego observando las posiciones relativas de otras marcas en las tiras. Los números alineados con las marcas dan el valor aproximado del producto, cociente u otro resultado calculado.

El usuario determina la ubicación del punto decimal en el resultado, basándose en una estimación mental. La notación científica se usa para rastrear el punto decimal en cálculos más formales. Los pasos de suma y resta en un cálculo generalmente se realizan mentalmente o en papel, no en la regla de cálculo.

Marcar un par de tarjetas de índice e introducir la base 2 con esta regla de diapositiva casera.

La mayoría de las reglas de cálculo constan de tres partes:

Marco o base – dos tiras lineales de la misma longitud mantenidas paralelamente con una brecha entre.
Diapositiva – una tira central entrelazada con el marco que puede mover longitudinalmente en relación con el marco.
Corredor o vidrio – una pieza deslizante exterior con una línea de pelo, también conocida como el "cursor".

Algunas reglas de cálculo (modelos "dúplex") tienen escalas en ambos lados de la regla y la tira deslizante, otras en un lado de las tiras exteriores y en ambos lados de la tira deslizante (que generalmente se puede tirar hacia afuera, volteada y reinsertada para mayor comodidad), y otras en un solo lado (reglas "simple"). Se utiliza un cursor deslizante con una línea de alineación vertical para encontrar los puntos correspondientes en escalas que no son adyacentes entre sí o, en modelos dúplex, están al otro lado de la regla. El cursor también puede registrar un resultado intermedio en cualquiera de las escalas.

Operación

Esta regla de diapositivas está posicionada para producir varios valores: De escala C a escala D (multiply by 2), de escala D a escala C (divide by 2), escalas A y B (multiply and divide by 4), escalas A y D (squares y raíces cuadradas).

Un logaritmo transforma las operaciones de multiplicación y división a adición y resta según las reglas $log(xy) = log(x) + log(y)$ y $log(x/y) = log(x) - log(y)$ . Mover la escala superior a la derecha por una distancia $log(x)$ , al igualar el comienzo de la escala superior con la etiqueta $x$ en el fondo, alinea cada número $y$ , en posición $log(y)$ en la escala superior, con el número en posición $log(x) + log(y)$ en la escala inferior. Porque... $log(x) + log(y) = log(xy)$ , esta posición en la escala inferior da $xy$ , el producto de $x$ y $y$ .

Multiplicación

Para multiplicar 3×2, el 1 de la escala superior se mueve al 2 de la escala inferior. La respuesta, 6, se lee en la escala inferior donde 3 está en la escala superior.

Para multiplicar 7×2, el 1 de la escala superior se mueve al 2 de la escala inferior. La respuesta, 14, se lee en la escala inferior donde 7 está en la escala superior. Dado que el 7 está por encima del segundo conjunto de números, el resultado debe multiplicarse por 10. Por lo tanto, aunque la respuesta sea directamente 1,4, la respuesta correcta es 1,4 x 10 = 14

Para multiplicar 88x20, el 1 de la escala superior se mueve al 2 de la escala inferior. Dado que 2 representa 20, todos los números de esa escala se multiplican por 10, por lo que cualquier respuesta en el segundo conjunto de números se multiplica por 100. Dado que 8,8 en la escala superior representa 88, la respuesta debe multiplicarse adicionalmente por 10. La respuesta respuesta directamente lee 1,76. Multiplique por 100 y luego por 10 para obtener la respuesta real: 1,760.

En general, el 1 en la parte superior se mueve a un factor en la parte inferior y la respuesta se lee en la parte inferior donde el otro factor está en la parte superior. Esto funciona porque las distancias desde el "1" son proporcionales a los logaritmos de los valores marcados.

División

La siguiente ilustración muestra el cálculo de 5,5/2. El 2 en la escala superior se coloca sobre el 5,5 en la escala inferior. El 1 en la escala superior se encuentra por encima del cociente, 2,75. Hay más de un método para hacer la división, y el método presentado aquí tiene la ventaja de que el resultado final no puede estar fuera de escala, porque uno tiene la opción de usar el 1 en cualquier extremo.

Con cálculos más complejos que involucran múltiples factores en el numerador y el denominador de una expresión, el movimiento de las escalas se puede minimizar alternando divisiones y multiplicaciones. Así (5,5×3)/2 se calcularía como (5,5/2)×3 y el resultado, 8,25, se puede leer debajo del 3 en la escala superior de la figura anterior, sin necesidad de registrar el resultado intermedio de 5,5 /2.

Otras operaciones

Además de las escalas logarítmicas, algunas reglas de cálculo tienen otras funciones matemáticas codificadas en otras escalas auxiliares. Los más populares son trigonométricos, generalmente seno y tangente, logaritmo común (log10) (para tomar el logaritmo de un valor en una escala multiplicadora), natural escalas logarítmicas (ln) y exponenciales (e^x). Algunas reglas incluyen una escala pitagórica ("P") para resolver triángulos. Otros cuentan con escalas para calcular funciones hiperbólicas. En las reglas lineales, las escalas y su etiquetado están altamente estandarizados, y la variación generalmente ocurre solo en términos de qué escalas se incluyen y en qué orden:

A, B	escalas logarítmicas de dos décadas, dos secciones cada una de las cuales es la mitad de la longitud de las escalas C y D, utilizadas para encontrar raíces cuadradas y cuadrados de números
C, D	escalas logarítmicas de una década, secciones únicas de la misma longitud, utilizadas juntas para la multiplicación y división, y generalmente una de ellas se combina con otra escala para otros cálculos
K	escala logarítmica de tres décadas, tres secciones cada una de las cuales es un tercio de la longitud de las escalas C y D, utilizado para encontrar raíces cubo y cubos de números
CF, DF	versiones "plegadas" de las escalas C y D que comienzan desde π en lugar de unidad; éstas son convenientes en dos casos. En primer lugar, cuando el usuario adivina que un producto estará cerca de 10 y no está seguro de si será ligeramente inferior o ligeramente superior a 10, las escalas plegadas evitan la posibilidad de salir de la escala. En segundo lugar, haciendo el inicio π en lugar de la raíz cuadrada de 10, multiplicando o dividiendo por π (como es común en las fórmulas de ciencia e ingeniería) es simplificado.
CI, DI, CIF, DIF	escalas "invertidas", que corren de derecha a izquierda, utilizadas para simplificar 1/x pasos
S	usado para encontrar pecados y cosines en la escala C (o D)
T, T1, T2	utilizado para encontrar tangentes y cotangentes en las escalas C y CI (o D y DI)
R1, R2	escalas de raíz cuadradas – establecer el cursor a cualquier valor $r$ en R1 o R2, encontrar ${displaystyle {pi }r^{2}}$ (área de un círculo de radio $r$ ) bajo el cursor en la escala DF
ST, SRT	utilizado para los pecados y tangentes de pequeños ángulos y conversión de grado-radiano
Sh, Sh1, Sh2	usado para encontrar pecados hiperbólicos en la escala C (o D)
Ch	utilizado para encontrar cosines hiperbólicos en la escala C (o D)
Th	utilizado para encontrar tangentes hiperbólicos en la escala C (o D)
L	una escala lineal, utilizada junto con las escalas C y D para encontrar logaritmos base-10 y poderes de 10
LL0N (o LL/N) y LLN	el log-log plegado $e^{-x}$ y $e^{x}$ escalas, para trabajar con logaritmos de cualquier base y exponentes arbitrarios. 4, 6, o 8 escalas de este tipo se ven comúnmente.
Ln	una escala lineal, utilizada junto con las escalas C y D para encontrar natural (base $e$ Logaritmos y $e^{x}$

Las escalas en la parte delantera y trasera de una regla de deslizamiento Keuffel y Esser (K PulE) 4081-3

La regla de cálculo binaria fabricada por Gilson en 1931 realizaba una función de suma y resta limitada a fracciones.

Raíces y poderes

Hay escalas de dos décadas (C y D), de dos décadas (A y B) y de tres décadas (K). Para calcular $x^{2}$ , por ejemplo, localizar x en la escala D y leer su cuadrado en la escala A. Invertir este proceso permite encontrar raíces cuadradas, y de forma similar para los poderes 3, 1/3, 2/3 y 3/2. Debe tomarse cuidado cuando la base, x, se encuentra en más de un lugar en su escala. Por ejemplo, hay dos nueves en la escala A; para encontrar la raíz cuadrada de nueve, utilice el primero; el segundo da la raíz cuadrada de 90.

Para $x^y$ problemas, use las escalas LL. Cuando varias escalas LL están presentes, use el x en ella. Primero, alinear la izquierda 1 en la escala C con x en la escala LL. Entonces, encuentra Sí. en la escala C y bajar a la escala LL con x en ella. Esa escala indicará la respuesta. Si Sí. es "de la escala", localizar $x^{y/2}$ y cuadrado utilizando las escalas A y B como se describe anteriormente. Alternativamente, use la más derecha 1 en la escala C, y lea la respuesta de la siguiente escala LL superior. Por ejemplo, alineando la más derecha 1 en la escala C con 2 en la escala LL2, 3 en la escala C hasta 8 en la escala LL3.

Para extraer una raíz cúbica usando una regla de cálculo con solo escalas C/D y A/B, alinee el 1 en el cursor B con el número base en la escala A (cuidando como siempre distinguir entre las mitades inferior y superior de la escala A). Deslice la diapositiva hasta que el número en la escala D que está contra 1 en el cursor C sea el mismo que el número en el cursor B que está contra el número base en la escala A. (Ejemplos: A 8, B 2, C 1, D 2; A 27, B 3, C 1, D 3.)

Raíces de ecuaciones cuadráticas

Ecuaciones cuadráticas de la forma $ax^{2}+bx+c=0$ se puede resolver reduciendo primero la ecuación a la forma ${displaystyle x^{2}-px+q=0}$ (donde) ${displaystyle p=-b/a}$ y $q = c/a$ ), y luego alinear el índice ("1") de la escala C al valor $q$ en la escala D. El cursor se mueve a lo largo de la regla hasta que se encuentra una posición donde los números de las escalas CI y D se suman a las $p$ . Estos dos valores son las raíces de la ecuación.

Trigonometría

Las escalas S, T y ST se utilizan para funciones trigonométricas y múltiplos de funciones trigonométricas, para ángulos en grados.

Para ángulos de alrededor de 5.7 hasta 90 grados, los pecados se encuentran comparando la escala S con escala C (o D). (En muchas reglas del cuerpo cerrado la escala S se relaciona con las escalas A y B y cubre ángulos de alrededor de 0,57 a 90 grados; lo que sigue debe ajustarse adecuadamente.) La escala S tiene un segundo conjunto de ángulos (a veces en un color diferente), que se ejecutan en la dirección opuesta, y se utilizan para cosines. Los tangentes se encuentran comparando la escala T con la escala C (o D) para ángulos inferiores a 45 grados. Para ángulos superiores a 45 grados se utiliza la escala CI. Formas comunes tales como $ksin x$ se puede leer directamente desde x en la escala S al resultado en la escala D, cuando el índice de escala C se establece enk. Para ángulos inferiores a 5.7 grados, los pecados, tangentes y radianos son aproximadamente iguales, y se encuentran en la escala ST o SRT (sines, radianos y tangentes), o simplemente divididos por 57.3 grados/radian. Las funciones trigonométricas inversas se encuentran revirtiendo el proceso.

Muchas reglas de cálculo tienen escalas S, T y ST marcadas con grados y minutos (por ejemplo, algunos modelos de Keuffel y Esser (modelos Doric dúplex de 5", por ejemplo), reglas de tipo Teledyne-Post Mannheim de último modelo). Los llamados modelos decitrig utilizan fracciones decimales de grados en su lugar.

Logaritmos y exponenciales

Los logaritmos y exponenciales de base 10 se calculan mediante la escala L, que es lineal. Algunas reglas de cálculo tienen una escala Ln, que es para la base e. Los logaritmos en cualquier otra base se pueden calcular invirtiendo el procedimiento para calcular potencias de un número. Por ejemplo, los valores de log2 se pueden determinar alineando el 1 más a la izquierda o más a la derecha en la escala C con el 2 en la escala LL2, encontrando el número cuyo logaritmo se calculará en la escala LL correspondiente y leyendo el valor log2 en la escala C. escala.

Sumas y restas

Normalmente, las reglas de cálculo no se usan para sumas y restas. Es posible hacerlo mediante dos técnicas diferentes.

El primer método para realizar sumas y restas en C y D (o cualquier escala comparable) requiere convertir el problema en uno de división. Para la suma, el cociente de las dos variables más uno por el divisor es igual a su suma:

{displaystyle x+y=left({frac {x}{y}}+1right)y.}

Para la resta, el cociente de las dos variables menos uno por el divisor es igual a su diferencia:

{displaystyle x-y=left({frac {x}{y}}-1right)y.}

Este método es similar a la técnica de suma/resta utilizada para circuitos electrónicos de alta velocidad con el sistema numérico logarítmico en aplicaciones informáticas especializadas como la supercomputadora Gravity Pipe (GRAPE) y los modelos ocultos de Markov.

El segundo método utiliza una escala L lineal deslizante disponible en algunos modelos. La suma y la resta se realizan deslizando el cursor hacia la izquierda (para la resta) o hacia la derecha (para la suma) y luego regresando la diapositiva a 0 para leer el resultado.

Generalizaciones

Escalas cuadráticas y recíprocas

Usando (casi) cualquier escala estrictamente monotónica, otros cálculos también se pueden hacer con un movimiento. Por ejemplo, las escalas recíprocas pueden utilizarse para la igualdad ${displaystyle {frac {1}{x}}+{frac {1}{y}}={frac {1}{z}}}$ (calculando resistencias paralelas, medios armónicos, etc.), y escalas cuadráticas se pueden utilizar para resolver ${displaystyle x^{2}+y^{2}=z^{2}}$ .

Diseño físico

Reglas lineales estándar

Una regla de deslizamiento de 7 pies (2,1 m) comparado con un modelo normal

El ancho de la regla de cálculo se expresa en términos del ancho nominal de las escalas. Escalas en el más común "10 pulgadas" los modelos miden en realidad 25 cm, ya que se fabricaron según los estándares métricos, aunque algunas reglas ofrecen escalas ligeramente más amplias para simplificar la manipulación cuando un resultado se desborda. Las reglas de bolsillo suelen ser de 5 pulgadas (12 cm). Se realizaron maquetas de un par de metros de ancho para ser colgadas en las aulas con fines didácticos.

Por lo general, las divisiones marcan una escala con una precisión de dos cifras significativas y el usuario estima la tercera cifra. Algunas reglas de cálculo de gama alta tienen cursores de aumento que facilitan la visualización de las marcas. Dichos cursores pueden duplicar efectivamente la precisión de las lecturas, lo que permite que una regla de cálculo de 10 pulgadas sirva tan bien como un modelo de 20 pulgadas.

Se han desarrollado otras comodidades. Las escalas trigonométricas a veces tienen doble etiqueta, en negro y rojo, con ángulos complementarios, el llamado "Darmstadt" estilo. Las reglas de cálculo dúplex a menudo duplican algunas de las escalas en la parte posterior. Las escalas a menudo se "dividen" para obtener mayor precisión.

Reglas de cálculo circulares

Las reglas de cálculo circulares vienen en dos tipos básicos, una con dos cursores y otra con un plato libre y un cursor. Las versiones de doble cursor realizan multiplicaciones y divisiones manteniendo un ángulo constante entre los cursores a medida que giran alrededor del dial. La versión de cursor de un solo pliegue funciona más como la regla de cálculo estándar a través de la alineación adecuada de las escalas.

La ventaja básica de una regla de cálculo circular es que la dimensión más ancha de la herramienta se redujo en un factor de aproximadamente 3 (es decir, por π). Por ejemplo, una circular de 10 cm tendría una precisión máxima aproximadamente igual a una regla de cálculo ordinaria de 31,4 cm. Las reglas de cálculo circulares también eliminan los errores "fuera de escala" cálculos, porque las escalas fueron diseñadas para "envolverse"; nunca tienen que ser reorientados cuando los resultados están cerca de 1.0—la regla siempre está a escala. Sin embargo, para escalas no espirales no cíclicas como S, T y LL's, el ancho de la escala se reduce para dejar espacio para los márgenes finales.

Las reglas de cálculo circulares son mecánicamente más resistentes y de movimiento más suave, pero la precisión de alineación de su escala es sensible al centrado de un pivote central; un minuto de 0,1 mm (0,0039 in) fuera del centro del pivote puede dar como resultado un error de alineación de 0,2 mm (0,0079 in) en el peor de los casos. El pivote evita que se raye la cara y los cursores. Las escalas de mayor precisión se colocan en los anillos exteriores. En lugar de "dividir" escalas, las reglas circulares de gama alta usan escalas espirales para operaciones más complejas como escalas logarítmicas. Una regla circular premium de ocho pulgadas tenía una escala logarítmica en espiral de 50 pulgadas. Alrededor de 1970, un modelo económico de B. C. Boykin (Modelo 510) presentaba 20 escalas, incluidas C-D (multiplicación) de 50 pulgadas y escalas logarítmicas. RotaRule presentaba un freno de fricción para el cursor.

Las principales desventajas de las reglas de cálculo circulares son la dificultad para ubicar figuras a lo largo de un plato y el número limitado de escalas. Otro inconveniente de las reglas de cálculo circulares es que las escalas menos importantes están más cerca del centro y tienen precisiones más bajas. La mayoría de los estudiantes aprendieron el uso de la regla de cálculo en las reglas de cálculo lineales y no encontraron motivos para cambiar.

Una regla de cálculo que aún se usa a diario en todo el mundo es la E6B. Esta es una regla de cálculo circular creada por primera vez en la década de 1930 para ayudar a los pilotos de aviones con la navegación a estima. Con la ayuda de escalas impresas en el marco, también ayuda con tareas diversas como convertir valores de tiempo, distancia, velocidad y temperatura, errores de brújula y calcular el uso de combustible. La llamada "rueda de oración" todavía está disponible en las tiendas de vuelos y sigue siendo ampliamente utilizado. Si bien el GPS ha reducido el uso de la navegación a estima para la navegación aérea y las calculadoras portátiles se han hecho cargo de muchas de sus funciones, el E6B sigue siendo ampliamente utilizado como dispositivo principal o de respaldo y la mayoría de las escuelas de vuelo exigen que sus estudiantes tengan algún grado de competencia. en su uso.

Las ruedas de proporción son reglas de cálculo circulares simples que se utilizan en el diseño gráfico para calcular las relaciones de aspecto. Al alinear los valores de tamaño original y deseado en las ruedas internas y externas, se mostrará su proporción como un porcentaje en una pequeña ventana. Aunque no son tan comunes desde la llegada del diseño computarizado, todavía se fabrican y utilizan.

En 1952, la empresa relojera suiza Breitling presentó un reloj de pulsera para piloto con una regla de cálculo circular integrada especializada en cálculos de vuelo: el Breitling Navitimer. La regla circular Navitimer, a la que Breitling se refiere como una 'computadora de navegación', presentaba funciones de velocidad aerodinámica, velocidad/tiempo de ascenso/descenso, tiempo de vuelo, distancia y consumo de combustible, así como kilómetro, milla náutica y funciones de conversión de cantidad de combustible en galones—litros.

Una simple regla circular de diapositivas, hecha por Concise Co., Ltd., Tokio, Japón, con escalas inversas, cuadradas y cúbicas. En el reverso hay una lista útil de 38 factores de conversión métrica/imperial.
Una regla de deslizamiento circular rusa construida como un reloj de bolsillo que funciona como regla de deslizamiento del cursor único, ya que las dos agujas están juntas
Una regla de deslizamiento de dos escalas construida en un anillo
Regla de diapositiva circular Pickett con dos cursores. (4.25 en/10.9 cm de ancho) El reverso tiene escala adicional y un cursor.
Breitling Navitimer reloj de pulsera con regla de diapositiva circular
El lado frontal de un modelo Boykin RotaRule 510
La parte trasera de un modelo Boykin RotaRule 510

Reglas de cálculo cilíndricas

Hay dos tipos principales de reglas de cálculo cilíndricas: las que tienen escalas helicoidales, como la calculadora Fuller, la regla de cálculo Otis King y Bygrave, y las que tienen barras, como la Thacher y algunos modelos de Loga. En cualquier caso, la ventaja es una escala mucho más larga y, por lo tanto, una precisión potencialmente mayor que la que ofrece una regla recta o circular.

Calculadora completa, 1928
Otis King Model K
Regla de diapositivas Bygrave
Regla de diapositivas Thacher, alrededor de 1890

Materiales

Tradicionalmente, las reglas de cálculo se fabricaban con madera dura, como caoba o boj, con cursores de vidrio y metal. Al menos un instrumento de alta precisión estaba hecho de acero.

En 1895, una empresa japonesa, Hemmi, comenzó a fabricar reglas de cálculo con bambú revestido de celuloide, que tenía la ventaja de ser dimensionalmente estable, fuerte y naturalmente autolubricante. Estas reglas de cálculo de bambú se introdujeron en Suecia en septiembre de 1933 y probablemente un poco antes en Alemania.

Las escalas también estaban hechas de celuloide u otros polímeros, o impresas en aluminio. Los cursores posteriores se moldearon con acrílicos o policarbonato, a veces con superficies de soporte de teflón.

Todas las reglas de cálculo premium tenían números y escalas profundamente grabados y luego se rellenaban con pintura u otra resina. Las reglas de cálculo pintadas o impresas se consideraban inferiores porque las marcas podían desgastarse o dañarse químicamente. Sin embargo, Pickett, una empresa estadounidense de reglas de cálculo, solo fabricaba reglas de escala impresas. Las reglas de cálculo premium incluían capturas inteligentes para que la regla no se desmoronara por accidente y parachoques para proteger la balanza y el cursor del roce con las mesas.

Historia

William Oughtred (1575-1660), inventor de la regla de la diapositiva

1763 ilustración de una regla de diapositivas

La regla de cálculo se inventó entre 1620 y 1630, poco después de la publicación del concepto de logaritmo por parte de John Napier. En 1620, Edmund Gunter de Oxford desarrolló un dispositivo de cálculo con una única escala logarítmica; con herramientas de medición adicionales podría usarse para multiplicar y dividir. Cª. 1622, William Oughtred de Cambridge combinó dos reglas portátiles de Gunter para crear un dispositivo que es reconociblemente la regla de cálculo moderna. Oughtred se vio envuelto en una controversia vitriólica sobre la prioridad, con su antiguo alumno Richard Delamain y los reclamos anteriores de Wingate. Las ideas de Oughtred solo se hicieron públicas en las publicaciones de su alumno William Forster en 1632 y 1653.

En 1677, Henry Coggeshall creó una regla plegable de dos pies para medir la madera, llamada regla de cálculo de Coggeshall, que amplió el uso de la regla de cálculo más allá de la investigación matemática.

En 1722, Warner introdujo las escalas de dos y tres décadas, y en 1755 Everard incluyó una escala invertida; una regla de cálculo que contiene todas estas escalas generalmente se conoce como "polifase" regla.

En 1815, Peter Mark Roget inventó la regla de cálculo log log, que incluía una escala que mostraba el logaritmo del logaritmo. Esto permitió al usuario realizar cálculos directamente con raíces y exponentes. Esto fue especialmente útil para potencias fraccionarias.

En 1821, Nathaniel Bowditch, describió en el American Practical Navigator una "regla de cálculo" que contenía funciones trigonométricas escaladas en la parte fija y una línea de log-sines y log-tans en el control deslizante utilizado para resolver problemas de navegación.

En 1845, Paul Cameron de Glasgow introdujo una regla de cálculo náutica capaz de responder preguntas de navegación, incluidas la ascensión recta y la declinación del sol y las estrellas principales.

Forma moderna

Ingeniero utilizando una regla de diapositivas, con calculadora mecánica en segundo plano, a mediados del siglo XX

Una forma más moderna de regla de cálculo fue creada en 1859 por el teniente de artillería francés Amédée Mannheim, quien tuvo la suerte de que una firma de reputación nacional hiciera su regla y la adoptara la artillería francesa. La regla de Mannheim tuvo dos modificaciones importantes que la hicieron más fácil de usar que las reglas de cálculo de uso general anteriores. Tales reglas tenían cuatro escalas básicas, A, B, C y D, y D era la única escala logarítmica de una sola década; C tenía dos décadas, como A y B. La mayoría de las operaciones se realizaron en las escalas A y B; D solo se usó para encontrar cuadrados y raíces cuadradas. Mannheim cambió la escala C a una escala de una sola década y realizó la mayoría de las operaciones con C y D en lugar de A y B. Debido a que las escalas C y D eran de una sola década, se podían leer con mayor precisión, por lo que la regla los resultados podrían ser más precisos. El cambio también facilitó la inclusión de cuadrados y raíces cuadradas como parte de un cálculo más amplio. La regla de Mannheim también tenía un cursor, a diferencia de casi todas las reglas anteriores, por lo que cualquiera de las escalas se podía comparar fácilmente en la cara de la regla. La "regla de Mannheim" se convirtió en el arreglo de regla de cálculo estándar para finales del siglo XIX y siguió siendo un estándar común a lo largo de la era de la regla de cálculo.

El crecimiento de la profesión de la ingeniería a finales del siglo XIX impulsó el uso generalizado de la regla de cálculo, comenzando en Europa y, finalmente, afianzándose también en los Estados Unidos. La regla dúplex fue inventada por William Cox en 1891 y fue producida por Keuffel and Esser Co. de Nueva York.

En 1881, el inventor estadounidense Edwin Thacher introdujo su regla cilíndrica, que tenía una escala mucho más larga que las reglas lineales estándar y, por lo tanto, podía calcular con mayor precisión, entre cuatro y cinco dígitos significativos. Sin embargo, la regla de Thacher era bastante costosa, además de no ser portátil, por lo que se usó en cantidades mucho más limitadas que las reglas de cálculo convencionales.

El trabajo astronómico también requería cálculos precisos y, en la Alemania del siglo XIX, se usaba una regla de cálculo de acero de unos dos metros de largo en un observatorio. Tenía un microscopio adjunto, lo que le daba una precisión de seis decimales.

En la década de 1920, el novelista e ingeniero Nevil Shute Noruega (llamó a su autobiografía Regla de cálculo) fue Jefe de cálculo en el diseño del dirigible británico R100 para Vickers Ltd. a partir de 1924. Los cálculos de tensión para cada marco transversal se requirieron cálculos por parte de un par de calculadoras (personas) usando las reglas de cálculo cilíndricas de Fuller durante dos o tres meses. La ecuación simultánea contenía hasta siete cantidades desconocidas, tomó alrededor de una semana para resolverse y tenía que repetirse con una selección diferente de cables flojos si la suposición sobre cuál de los ocho cables radiales estaba flojo era incorrecta y uno de los cables se suponía que estaba flojo. ser flojo no era flojo. Después de meses de trabajo llenando quizás cincuenta hojas de papel con cálculos 'la verdad quedó revelada' (y) produjo una satisfacción casi equivalente a una experiencia religiosa".

Durante las décadas de 1950 y 1960, la regla de cálculo fue el símbolo de la profesión de ingeniero de la misma manera que el estetoscopio lo es de la profesión médica.

El científico espacial alemán Wernher von Braun compró dos reglas de cálculo Nestler en la década de 1930. Diez años después, los trajo consigo cuando se mudó a los EE. UU. después de la Segunda Guerra Mundial para trabajar en el esfuerzo espacial estadounidense. A lo largo de su vida nunca utilizó ninguna otra regla de cálculo. Usó sus dos Nestler mientras dirigía el programa de la NASA que llevó a un hombre a la Luna en julio de 1969.

Las reglas de cálculo de la marca Pickett de aluminio se llevaron a cabo en las misiones espaciales del Proyecto Apolo. El modelo N600-ES propiedad de Buzz Aldrin que voló con él a la Luna en el Apolo 11 se vendió en una subasta en 2007. El modelo N600-ES que se llevó en el Apolo 13 en 1970 es propiedad del Museo Nacional del Aire y el Espacio.

Algunos estudiantes de ingeniería e ingenieros llevaban reglas de cálculo de diez pulgadas en fundas de cinturón, algo común en los campus incluso a mediados de la década de 1970. Hasta la llegada de la calculadora digital de bolsillo, los estudiantes también podían tener una regla de diez o veinte pulgadas para trabajos de precisión en casa o en la oficina mientras llevaban consigo una regla de cálculo de bolsillo de cinco pulgadas.

En 2004, los investigadores en educación David B. Sher y Dean C. Nataro concibieron un nuevo tipo de regla de cálculo basada en la prostaféresis, un algoritmo para calcular rápidamente productos que es anterior a los logaritmos. Sin embargo, ha habido poco interés práctico en construir uno más allá del prototipo inicial.

Calculadoras especializadas

Las reglas de cálculo a menudo se han especializado en diversos grados para su campo de uso, como impuestos especiales, cálculo de prueba, ingeniería, navegación, etc., y algunas reglas de cálculo son extremadamente especializadas para aplicaciones muy limitadas. Por ejemplo, John Rabone & El catálogo de Sons 1892 enumera una "Cinta métrica y calibre de ganado", un dispositivo para estimar el peso de una vaca a partir de sus medidas.

Había muchas reglas de cálculo especializadas para aplicaciones fotográficas; por ejemplo, el actinógrafo de Hurter y Driffield era un dispositivo de dos correderas de madera de boj, latón y cartón para estimar la exposición a partir de la hora del día, la época del año y la latitud.

Se inventaron reglas de cálculo especializadas para diversas formas de ingeniería, negocios y banca. Estos a menudo tenían cálculos comunes expresados directamente como escalas especiales, por ejemplo, cálculos de préstamos, cantidades de compra óptimas o ecuaciones de ingeniería particulares. Por ejemplo, la empresa Fisher Controls distribuyó una regla de cálculo personalizada adaptada para resolver las ecuaciones utilizadas para seleccionar el tamaño adecuado de las válvulas de control de flujo industrial.

Los meteorólogos de los servicios meteorológicos utilizaron las reglas de cálculo de los globos piloto para determinar las velocidades superiores del viento de un globo piloto ascendente lleno de hidrógeno o helio.

La E6-B es una regla de cálculo circular utilizada por pilotos y navegantes.

Las reglas de cálculo circulares para estimar las fechas de ovulación y la fertilidad se conocen como calculadoras de ruedas.

Una publicación del Departamento de Defensa de 1962 incluía una regla de cálculo circular de propósito especial para calcular los efectos de la explosión, la sobrepresión y la exposición a la radiación de una bomba atómica dada.

Un ordenador de aviación E6-B
John Rabone " Sons 1892 ganadero
El actinógrafo de Hurter y Driffield
Regla de diapositiva críptográfica utilizada por el ejército suizo entre 1914 y 1940

Rechazar

La calculadora científica TI-30, presentada por menos de US$25 en 1976

La importancia de la regla de cálculo comenzó a disminuir a medida que las computadoras electrónicas, un recurso nuevo pero escaso en la década de 1950, estuvieron más disponibles para los trabajadores técnicos durante la década de 1960.

Otro paso para alejarse de las reglas de cálculo fue la introducción de calculadoras científicas electrónicas de escritorio relativamente económicas. El primero incluyó Wang Laboratories LOCI-2, introducido en 1965, que usaba logaritmos para la multiplicación y la división; y el Hewlett-Packard HP 9100A, presentado en 1968. Ambos eran programables y proporcionaban funciones exponenciales y logarítmicas; el HP tenía funciones trigonométricas (seno, coseno y tangente) y también funciones trigonométricas hiperbólicas. El HP usó el algoritmo CORDIC (computadora digital de rotación de coordenadas), que permite el cálculo de funciones trigonométricas usando solo operaciones de cambio y suma. Este método facilitó el desarrollo de calculadoras científicas cada vez más pequeñas.

Al igual que con la computación central, la disponibilidad de estas máquinas no afectó significativamente el uso ubicuo de la regla de cálculo hasta que las calculadoras electrónicas científicas de mano baratas estuvieron disponibles a mediados de la década de 1970, momento en el cual disminuyó rápidamente. La calculadora científica de bolsillo Hewlett-Packard HP-35 fue el primer dispositivo portátil de este tipo, pero costó 395 dólares en 1972. Esto era justificable para algunos profesionales de la ingeniería pero demasiado caro para la mayoría de los estudiantes.

Alrededor de 1974, la calculadora científica electrónica portátil dejó obsoletas las reglas de cálculo. Para 1975, las calculadoras electrónicas básicas de cuatro funciones se podían comprar por menos de $50, y para 1976, la calculadora científica TI-30 se vendía por menos de $25 ($119 ajustados por inflación).

1980 fue el último año en la escuela de Texas U.I.L. competencia para usar concurso de regla de cálculo. La Liga Interescolar Universitaria se organizó en 1910. Originalmente, la U.I.L. se formó para administrar eventos literarios, pero también se convirtió en el órgano rector de los eventos deportivos escolares.

Comparación con calculadoras digitales electrónicas

Diciembre de 1951 anuncio para el IBM 604 Electronic Calculating Punch comparando explícitamente computadoras electrónicas con ingenieros calculando con reglas de diapositivas

Incluso durante su apogeo, las reglas de cálculo nunca se hicieron populares entre el público en general. La suma y la resta no son operaciones compatibles con las reglas de cálculo y hacer un cálculo con una regla de cálculo tiende a ser más lento que con una calculadora. Esto llevó a los ingenieros a usar ecuaciones matemáticas que favorecían las operaciones que eran fáciles con una regla de cálculo en lugar de funciones más precisas pero complejas; estas aproximaciones podrían dar lugar a inexactitudes y errores. Por otro lado, la operación manual espacial de las reglas de cálculo cultiva en el usuario una intuición para las relaciones numéricas y la escala que a menudo les falta a las personas que solo han usado calculadoras digitales. Una regla de cálculo también mostrará todos los términos de un cálculo junto con el resultado, eliminando así la incertidumbre sobre qué cálculo se realizó realmente.

Una regla de cálculo requiere que el usuario calcule por separado el orden de magnitud de la respuesta para colocar el punto decimal en los resultados. Por ejemplo, 1,5 × 30 (que equivale a 45) mostrará el mismo resultado que 1 500 000 × 0,03 (que equivale a 45 000). Este cálculo separado obliga al usuario a realizar un seguimiento de la magnitud en la memoria a corto plazo (que es propensa a errores), tomar notas (lo que es engorroso) o razonar al respecto en cada paso (lo que lo distrae de los otros requisitos de cálculo).

La precisión aritmética típica de una regla de cálculo es de unos tres dígitos significativos, en comparación con los muchos dígitos de las calculadoras digitales. Como el orden de magnitud adquiere la mayor importancia cuando se usa una regla de cálculo, es menos probable que los usuarios cometan errores de falsa precisión.

Al realizar una secuencia de multiplicaciones o divisiones por el mismo número, la respuesta a menudo se puede determinar simplemente mirando la regla de cálculo sin ninguna manipulación. Esto puede ser especialmente útil al calcular porcentajes (p. ej., para puntajes de exámenes) o al comparar precios (p. ej., en dólares por kilogramo). Se pueden realizar múltiples cálculos de velocidad-tiempo-distancia con manos libres de un vistazo con una regla de cálculo. Otras conversiones lineales útiles, como libras a kilogramos, se pueden marcar fácilmente en la regla y usar directamente en los cálculos.

Al ser totalmente mecánica, una regla de cálculo no depende de la red eléctrica ni de las baterías. Sin embargo, la imprecisión mecánica en las reglas de cálculo mal construidas o deformadas por el calor o el uso dará lugar a errores.

Muchos navegantes mantienen reglas de cálculo como respaldo para la navegación en caso de falla eléctrica o agotamiento de la batería en segmentos de ruta largos. Las reglas de cálculo todavía se usan comúnmente en la aviación, particularmente para aviones más pequeños. Están siendo reemplazadas solo por computadoras de vuelo integradas, de propósito especial y costosas, y no por calculadoras de propósito general. La regla de cálculo circular E6B utilizada por los pilotos ha estado en producción continua y sigue estando disponible en una variedad de modelos. Algunos relojes de pulsera diseñados para uso en la aviación todavía cuentan con escalas de regla de cálculo para permitir cálculos rápidos. El Citizen Skyhawk AT y el Seiko Flightmaster SNA411 son dos ejemplos notables.

Uso contemporáneo

Regla de diapositivas Faber-Castell con bolsa

Incluso en el siglo XXI, algunas personas prefieren una regla de cálculo a una calculadora electrónica como dispositivo informático práctico. Otros conservan sus viejas reglas de cálculo por nostalgia o las coleccionan como pasatiempo.

Un modelo coleccionable popular es el Keuffel & Esser Deci-Lon, una regla de cálculo científica y de ingeniería de primera calidad disponible en formato de diez pulgadas (25 cm) "regular" (Deci-Lon 10) y un "bolsillo" de cinco pulgadas; (Deci-Lon 5) variante. Otro modelo estadounidense preciado es la regla circular de Scientific Instruments de ocho pulgadas (20 cm). De las normas europeas, los modelos de gama alta de Faber-Castell son los más populares entre los coleccionistas.

Aunque circulan muchas reglas de cálculo en el mercado, los especímenes en buenas condiciones tienden a ser costosos. Muchas reglas que se encuentran a la venta en los sitios de subastas en línea están dañadas o les faltan piezas, y es posible que el vendedor no sepa lo suficiente como para proporcionar la información pertinente. Las piezas de repuesto son escasas, caras y, por lo general, solo están disponibles para su compra por separado en coleccionistas individuales. sitios web Las reglas de Keuffel y Esser desde el período hasta alrededor de 1950 son particularmente problemáticas, porque los extremos de los cursores, hechos de celuloide, tienden a descomponerse químicamente con el tiempo.

Todavía hay un puñado de fuentes para nuevas reglas de cálculo. The Concise Company of Tokyo, que comenzó como fabricante de reglas de cálculo circulares en julio de 1954, continúa fabricándolas y vendiéndolas en la actualidad. En septiembre de 2009, el minorista en línea ThinkGeek introdujo su propia marca de reglas de cálculo directas, descritas como "réplica[s] fiel[s]" que son "elaborados a mano individualmente". Estos ya no estaban disponibles en 2012. Además, Faber-Castell tenía varias reglas de cálculo en inventario, disponibles para compra internacional a través de su tienda web, hasta mediados de 2018. Las ruedas proporcionales todavía se usan en diseño gráfico.

Hay varias aplicaciones de simulación de reglas de cálculo disponibles para teléfonos inteligentes y tabletas basados en Android e iOS.

Las reglas de cálculo especializadas, como la E6B que se usa en la aviación, y las reglas de cálculo de artillería que se usan para colocar artillería, todavía se usan, aunque ya no de manera rutinaria. Estas reglas se usan como parte del proceso de enseñanza e instrucción ya que al aprender a usarlas el estudiante también aprende sobre los principios detrás de los cálculos, también le permite al estudiante poder usar estos instrumentos como respaldo en caso de que los modernos la electrónica de uso general falla.

Colecciones

Una regla de diapositiva grande que se muestra en el Museo MIT

El Museo del MIT en Cambridge, Massachusetts, tiene una colección de cientos de reglas de cálculo, nomogramas y calculadoras mecánicas. La colección de Keuffel and Esser Company, del fabricante de reglas de cálculo anteriormente ubicado en Brooklyn, Nueva York, fue donada al MIT alrededor de 2005. Los artículos seleccionados de la colección generalmente se exhiben en el Museo.

Se dice que el Museo Internacional de Reglas de Cálculo es "[el mundo's] recurso más extenso para todo lo relacionado con reglas de cálculo y calculadoras logarítmicas". La página web del museo incluye literatura relacionada con las reglas de cálculo en su "Biblioteca de reglas de cálculo" sección.

Contenido relacionado

Más resultados...