Reconstrucción iterativa

Reconstrucción iterativa se refiere a algoritmos iterativos utilizados para reconstruir imágenes 2D y 3D en determinadas técnicas de imagen. Por ejemplo, en la tomografía computarizada se debe reconstruir una imagen a partir de proyecciones de un objeto. En este caso, las técnicas de reconstrucción iterativa suelen ser una alternativa mejor, pero computacionalmente más costosa, al método común de retroproyección filtrada (FBP), que calcula directamente la imagen en un solo paso de reconstrucción. En trabajos de investigación recientes, los científicos han demostrado que es posible realizar cálculos extremadamente rápidos y un paralelismo masivo para la reconstrucción iterativa, lo que hace que la reconstrucción iterativa sea práctica para la comercialización.

Conceptos básicos

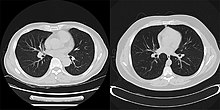
La reconstrucción de una imagen a partir de los datos adquiridos es un problema inverso. A menudo no es posible resolver exactamente la inversa. problema directamente. En este caso, un algoritmo directo tiene que aproximarse a la solución, lo que podría provocar artefactos de reconstrucción visibles en la imagen. Los algoritmos iterativos abordan la solución correcta utilizando múltiples pasos de iteración, lo que permite obtener una mejor reconstrucción a costa de un mayor tiempo de cálculo.

Existe una gran variedad de algoritmos, pero cada uno comienza con una imagen supuesta, calcula proyecciones a partir de la imagen, compara los datos de la proyección original y actualiza la imagen en función de la diferencia entre las proyecciones calculadas y reales.

Reconstrucción algebraica

La Técnica de Reconstrucción Algebraica (ART) fue la primera técnica de reconstrucción iterativa utilizada para la tomografía computarizada por Hounsfield.

Varianza mínima asintótica dispersa iterativa

El algoritmo iterativo de varianza mínima asintótica dispersa es un método iterativo de reconstrucción tomográfica de superresolución sin parámetros inspirado en la detección comprimida, con aplicaciones en radar de apertura sintética, tomografía computarizada e imágenes por resonancia magnética (MRI).

Reconstrucción estadística

Los algoritmos estadísticos iterativos de reconstrucción de imágenes suelen tener cinco componentes, p.

1. Un modelo de objeto que expresa la función de espacio continuo desconocida ${displaystyle f(r)}$ que debe ser reconstruido en términos de una serie finita con coeficientes desconocidos que deben ser estimados de los datos.
2. Un modelo de sistema que relaciona el objeto desconocido con las mediciones "ideales" que se registrarían en ausencia de ruido de medición. A menudo este es un modelo lineal de la forma ${displaystyle mathbf {A} x+epsilon }$, donde ${displaystyle epsilon }$ representa el ruido.
3. Un modelo estadístico que describe cómo las mediciones ruidosas varían alrededor de sus valores ideales. A menudo se asume el ruido gaissiano o las estadísticas de Poisson. Debido a que las estadísticas de Poisson están más cerca de la realidad, es más ampliamente utilizado.
4. Una función de coste que debe minimizarse para estimar el vector de coeficiente de imagen. A menudo esta función de costo incluye alguna forma de regularización. A veces la regularización se basa en campos al azar de Markov.
5. Un algoritmo, generalmente iterativo, para minimizar la función de coste, incluyendo una estimación inicial de la imagen y algún criterio de parada para terminar las iteraciones.

Reconstrucción iterativa aprendida

En la reconstrucción iterativa aprendida, el algoritmo de actualización se aprende a partir de datos de entrenamiento utilizando técnicas de aprendizaje automático, como redes neuronales convolucionales, sin dejar de incorporar el modelo de formación de imágenes. Por lo general, esto proporciona reconstrucciones más rápidas y de mayor calidad y se ha aplicado a la reconstrucción por TC y RM.

Ventajas

Las ventajas del enfoque iterativo incluyen una mayor insensibilidad al ruido y la capacidad de reconstruir una imagen óptima en el caso de datos incompletos. El método se ha aplicado en modalidades de tomografía por emisión como SPECT y PET, donde hay una atenuación significativa a lo largo de las trayectorias de los rayos y las estadísticas de ruido son relativamente pobres.

Enfoques estadísticos basados en la probabilidad: algoritmos iterativos de maximización de expectativas estadísticos basados en la probabilidad son ahora el método preferido de reconstrucción. Dichos algoritmos calculan estimaciones de la distribución probable de los eventos de aniquilación que condujeron a los datos medidos, basándose en principios estadísticos, y a menudo proporcionan mejores perfiles de ruido y resistencia a los artefactos de racha comunes con FBP. Dado que la densidad del trazador radiactivo es una función en un espacio funcional y, por lo tanto, de dimensiones extremadamente altas, los métodos que regularizan la solución de máxima verosimilitud y la convierten en métodos penalizados o máximos a posteriori pueden tener ventajas significativas para recuentos bajos. Ejemplos como el estimador Sieve de Ulf Grenander o métodos de penalización de Bayes, o mediante I.J. El método de rugosidad de Good puede producir un rendimiento superior a los métodos basados en la maximización de expectativas que involucran únicamente una función de probabilidad de Poisson.

Como otro ejemplo, se considera superior cuando no se tiene un gran conjunto de proyecciones disponibles, cuando las proyecciones no están distribuidas uniformemente en ángulo, o cuando las proyecciones son escasas o faltan en ciertas orientaciones. Estos escenarios pueden ocurrir en la TC intraoperatoria, en la TC cardíaca o cuando se encuentran artefactos metálicos. requieren la exclusión de algunas partes de los datos de proyección.

En Imágenes por Resonancia Magnética se puede utilizar para reconstruir imágenes a partir de datos adquiridos con múltiples bobinas receptoras y con patrones de muestreo diferentes de la cuadrícula cartesiana convencional y permite el uso de técnicas de regularización mejoradas (por ejemplo, variación total) o un modelado extendido de imágenes físicas. procesos para mejorar la reconstrucción. Por ejemplo, con algoritmos iterativos es posible reconstruir imágenes a partir de datos adquiridos en muy poco tiempo como se requiere para la resonancia magnética en tiempo real (rt-MRI).

En la tomografía crioelectrónica, donde se adquiere un número limitado de proyecciones debido a las limitaciones del hardware y para evitar daños a la muestra biológica, se puede utilizar junto con técnicas de detección de compresión o funciones de regularización (por ejemplo, función de Huber) para mejorar la reconstrucción. para una mejor interpretación.

A continuación se muestra un ejemplo que ilustra los beneficios de la reconstrucción iterativa de imágenes para la resonancia magnética cardíaca.