Razonamiento inductivo

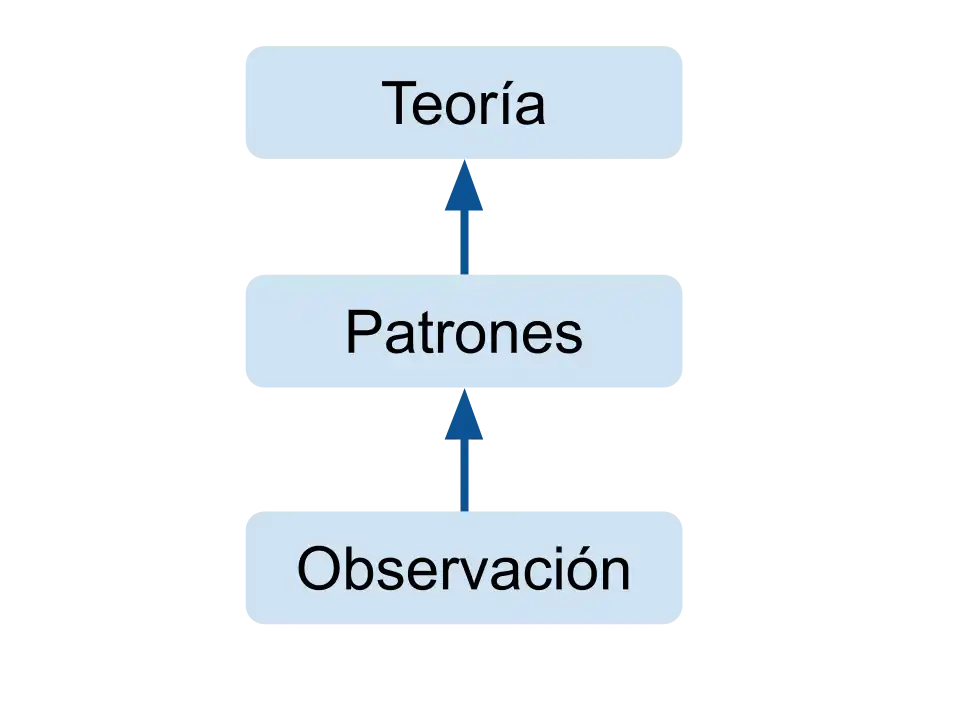
El razonamiento inductivo es un método de razonamiento en el que se considera que un conjunto de observaciones deriva un principio general. Consiste en hacer amplias generalizaciones basadas en observaciones específicas. El razonamiento inductivo es distinto del razonamiento deductivo. Si las premisas son correctas, la conclusión de un argumento deductivo es cierta; por el contrario, la verdad de la conclusión de un argumento inductivo es probable, con base en la evidencia dada.

Tipos

Los tipos de razonamiento inductivo incluyen generalización, predicción, silogismo estadístico, argumento por analogía e inferencia causal.

Generalización inductiva

Una generalización (más exactamente, una generalización inductiva) procede de una premisa sobre una muestra a una conclusión sobre la población. La observación obtenida de esta muestra se proyecta a la población más amplia.La proporción Q de la muestra tiene el atributo A.Por tanto, la proporción Q de la población tiene el atributo A.

Por ejemplo, digamos que hay 20 bolas, ya sean negras o blancas, en una urna. Para estimar sus números respectivos, extrae una muestra de cuatro bolas y encuentra que tres son negras y una es blanca. Una generalización inductiva sería que hay 15 bolas negras y 5 blancas en la urna.

La medida en que las premisas respalden la conclusión depende de (1) el número en el grupo de muestra, (2) el número en la población y (3) el grado en que la muestra representa a la población (que puede lograrse tomando una muestra aleatoria). muestra). Cuanto mayor sea el tamaño de la muestra en relación con la población y cuanto más fielmente represente la muestra a la población, más fuerte será la generalización. La generalización apresurada y la muestra sesgada son falacias de generalización.

Generalización estadística

Una generalización estadística es un tipo de argumento inductivo en el que se infiere una conclusión sobre una población utilizando una muestra estadísticamente representativa. Por ejemplo:De una muestra aleatoria considerable de votantes encuestados, el 66 % apoya la Medida Z.Por lo tanto, aproximadamente el 66 % de los votantes apoya la Medida Z.

La medida es altamente confiable dentro de un margen de error bien definido siempre que la muestra sea grande y aleatoria. Es fácilmente cuantificable. Compare el argumento anterior con el siguiente. "Seis de las diez personas en mi club de lectura son libertarios. Por lo tanto, alrededor del 60% de las personas son libertarios". El argumento es débil porque la muestra no es aleatoria y el tamaño de la muestra es muy pequeño.

Las generalizaciones estadísticas también se denominan proyecciones estadísticas y proyecciones muestrales.

Generalización anecdótica

Una generalización anecdótica es un tipo de argumento inductivo en el que se infiere una conclusión sobre una población utilizando una muestra no estadística. En otras palabras, la generalización se basa en evidencia anecdótica. Por ejemplo:Hasta ahora, este año el equipo de Pequeñas Ligas de su hijo ha ganado 6 de 10 juegos.Por lo tanto, al final de la temporada habrán ganado alrededor del 60% de los juegos.

Esta inferencia es menos confiable (y, por lo tanto, es más probable que cometa la falacia de la generalización apresurada) que una generalización estadística, primero, porque los eventos de la muestra no son aleatorios y, segundo, porque no se puede reducir a una expresión matemática. Estadísticamente hablando, simplemente no hay forma de saber, medir y calcular las circunstancias que afectan el desempeño que se obtendrá en el futuro. A nivel filosófico, el argumento se basa en la presuposición de que la operación de eventos futuros reflejará el pasado. En otras palabras, da por sentada una uniformidad de la naturaleza, un principio no probado que no puede derivarse de los datos empíricos mismos. Los argumentos que presuponen tácitamente esta uniformidad a veces se denominan argumentos humeanos.después del filósofo que fue el primero en someterlos al escrutinio filosófico.

Predicción

Una predicción inductiva extrae una conclusión sobre una instancia futura, actual o pasada de una muestra de otras instancias. Al igual que una generalización inductiva, una predicción inductiva se basa en un conjunto de datos que consta de instancias específicas de un fenómeno. Pero en lugar de concluir con una declaración general, la predicción inductiva concluye con una declaración específica sobre la probabilidad de que una sola instancia tenga (o no) un atributo compartido (o no compartido) por las otras instancias.La proporción Q de los miembros observados del grupo G ha tenido el atributo A.Por lo tanto, existe una probabilidad correspondiente a Q de que otros miembros del grupo G tengan el atributo A la próxima vez que se observen.

Silogismo estadístico

Un silogismo estadístico procede de una generalización sobre un grupo a una conclusión sobre un individuo.La proporción Q de las instancias conocidas de la población P tiene el atributo A.El individuo I es otro miembro de P.Por lo tanto, existe una probabilidad correspondiente a Q de que I tenga A.

Por ejemplo:El 90% de los graduados de la escuela Preparatoria Excelsior van a la Universidad.Bob se graduó de la escuela preparatoria Excelsior.Por lo tanto, Bob irá a la Universidad.

Este es un silogismo estadístico. Aunque no se puede estar seguro de que Bob asistirá a la universidad, podemos estar totalmente seguros de la probabilidad exacta de este resultado (sin más información). Podría decirse que el argumento es demasiado fuerte y podría ser acusado de "hacer trampa". Después de todo, la probabilidad está dada en la premisa. Normalmente, el razonamiento inductivo busca formular una probabilidad. Dos falacias de dicto simpliciter pueden ocurrir en silogismos estadísticos: "accidente" y "accidente inverso".

Argumento por analogía

El proceso de inferencia analógica implica observar las propiedades compartidas de dos o más cosas y, a partir de esta base, inferir que también comparten alguna propiedad adicional:P y Q son similares con respecto a las propiedades a, b y c.Se ha observado que el objeto P tiene además la propiedad x.Por lo tanto, Q probablemente también tenga la propiedad x.

El razonamiento analógico es muy frecuente en el sentido común, la ciencia, la filosofía, el derecho y las humanidades, pero a veces se acepta sólo como método auxiliar. Un enfoque refinado es el razonamiento basado en casos.El Mineral A y el Mineral B son rocas ígneas que a menudo contienen vetas de cuarzo y se encuentran más comúnmente en América del Sur en áreas de actividad volcánica antigua.El mineral A también es una piedra blanda adecuada para tallar joyas.Por lo tanto, el mineral B es probablemente una piedra blanda adecuada para tallar joyas.

Esta es la inducción analógica, según la cual las cosas similares en ciertos aspectos son más propensas a ser similares en otros. Esta forma de inducción fue explorada en detalle por el filósofo John Stuart Mill en su System of Logic, donde afirma: "[n]o puede haber ninguna duda de que toda semejanza [que no se sabe que es irrelevante] ofrece cierto grado de probabilidad, más allá de lo que existiría de otro modo, a favor de la conclusión". Ver Métodos de Mill.

Algunos pensadores sostienen que la inducción analógica es una subcategoría de la generalización inductiva porque asume una uniformidad preestablecida que gobierna los eventos. La inducción analógica requiere un examen auxiliar de la pertinencia de las características citadas como comunes al par. En el ejemplo anterior, si se agregara una premisa que establece que ambas piedras fueron mencionadas en los registros de los primeros exploradores españoles, este atributo común es extraño a las piedras y no contribuye a su probable afinidad.

Un escollo de la analogía es que las características pueden seleccionarse cuidadosamente: mientras que los objetos pueden mostrar similitudes sorprendentes, dos cosas yuxtapuestas pueden poseer, respectivamente, otras características no identificadas en la analogía que son características marcadamente diferentes. Por lo tanto, la analogía puede inducir a error si no se realizan todas las comparaciones pertinentes.

Inferencia causal

Una inferencia causal extrae una conclusión sobre una conexión causal basada en las condiciones de ocurrencia de un efecto. Las premisas sobre la correlación de dos cosas pueden indicar una relación causal entre ellas, pero se deben confirmar factores adicionales para establecer la forma exacta de la relación causal.

Métodos

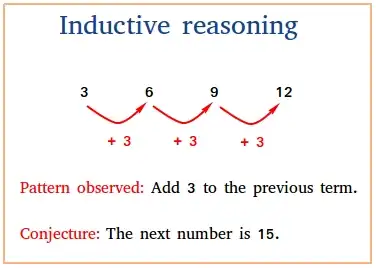
Los dos métodos principales utilizados para llegar a conclusiones inductivas son la inducción enumerativa y la inducción eliminativa.

Inducción enumerativa

La inducción enumerativa es un método inductivo en el que se construye una conclusión en función del número de instancias que la respaldan. Cuantas más instancias de apoyo, más fuerte es la conclusión.

La forma más básica de inducción enumerativa razona desde instancias particulares a todas las instancias y, por lo tanto, es una generalización sin restricciones. Si uno observa 100 cisnes, y los 100 eran blancos, uno podría inferir una proposición categórica universal de la forma Todos los cisnes son blancos. Como las premisas de esta forma de razonamiento, aunque sean verdaderas, no implican la verdad de la conclusión, esta es una forma de inferencia inductiva. La conclusión puede ser verdadera y puede pensarse que es probablemente verdadera, pero puede ser falsa. Las preguntas sobre la justificación y la forma de las inducciones enumerativas han sido centrales en la filosofía de la ciencia, ya que la inducción enumerativa tiene un papel fundamental en el modelo tradicional del método científico.Todas las formas de vida descubiertas hasta ahora están compuestas de células.Por lo tanto, todas las formas de vida están compuestas de células.

Esta es la inducción enumerativa, también conocida como inducción simple o inducción predictiva simple. Es una subcategoría de la generalización inductiva. En la práctica diaria, esta es quizás la forma más común de inducción. Para el argumento anterior, la conclusión es tentadora pero hace una predicción muy por encima de la evidencia. Primero, asume que las formas de vida observadas hasta ahora pueden decirnos cómo serán los casos futuros: una apelación a la uniformidad. En segundo lugar, el Todo concluyente es una afirmación audaz. Un solo caso contrario frustra el argumento. Y por último, cuantificar el nivel de probabilidad en cualquier forma matemática es problemático.¿Con qué estándar medimos nuestra muestra terrestre de vida conocida contra toda vida (posible)? Supongamos que descubrimos algún organismo nuevo, como un microorganismo que flota en la mesosfera o un asteroide, y es celular. ¿La adición de esta evidencia corroborante nos obliga a elevar nuestra evaluación de probabilidad para la proposición del sujeto? En general, se considera razonable responder a esta pregunta "sí", y para muchos este "sí" no solo es razonable sino incontrovertible. Entonces, ¿cuánto deberían cambiar estos nuevos datos nuestra evaluación de probabilidad? Aquí, el consenso se desvanece y en su lugar surge la pregunta de si podemos hablar de probabilidad de manera coherente sin cuantificación numérica.Todas las formas de vida descubiertas hasta ahora se han compuesto de células.Por lo tanto, la próxima forma de vida que se descubra estará compuesta por células.

Esta es la inducción enumerativa en su forma débil. Trunca "todos" a una mera instancia única y, al hacer una afirmación mucho más débil, fortalece considerablemente la probabilidad de su conclusión. De lo contrario, tiene las mismas deficiencias que la forma fuerte: su muestra de población no es aleatoria y los métodos de cuantificación son difíciles de alcanzar.

Inducción eliminativa

La inducción eliminativa, también llamada inducción variable, es un método inductivo en el que se construye una conclusión a partir de la variedad de instancias que la sustentan. A diferencia de la inducción enumerativa, la inducción eliminativa razona en función de los diversos tipos de instancias que respaldan una conclusión, en lugar de la cantidad de instancias que la respaldan. A medida que aumenta la variedad de instancias, más conclusiones posibles basadas en esas instancias pueden identificarse como incompatibles y eliminarse. Esto, a su vez, aumenta la fuerza de cualquier conclusión que se mantenga consistente con las diversas instancias. Este tipo de inducción puede utilizar diferentes metodologías, como la cuasi-experimentación, que prueba y, en lo posible, elimina hipótesis rivales.También se pueden emplear diferentes pruebas probatorias para eliminar las posibilidades que se contemplan.

La inducción eliminativa es crucial para el método científico y se utiliza para eliminar hipótesis que son inconsistentes con las observaciones y experimentos. Se centra en las causas posibles en lugar de las instancias reales observadas de conexiones causales.

Historia

Filosofía antigua

Para pasar de lo particular a lo universal, Aristóteles en el año 300 a. C. usó la palabra griega epagogé, que Cicerón tradujo a la palabra latina inductio.

Aristóteles y la escuela peripatética

Los Análisis posteriores de Aristóteles cubren los métodos de prueba inductiva en la filosofía natural y en las ciencias sociales. El primer libro de los Analíticos posteriores describe la naturaleza y la ciencia de la demostración y sus elementos: incluyendo la definición, la división, la razón intuitiva de los primeros principios, la demostración particular y universal, la demostración afirmativa y negativa, la diferencia entre ciencia y opinión, etc.

Pirronismo

Los antiguos pirronistas fueron los primeros filósofos occidentales en señalar el Problema de la inducción: que la inducción no puede, según ellos, justificar la aceptación de enunciados universales como verdaderos.

Medicina antigua

La escuela empírica de la medicina griega antigua empleó el epilogismo como método de inferencia. El 'epilogismo' es un método libre de teoría que analiza la historia a través de la acumulación de hechos sin mayor generalización y considerando las consecuencias de hacer afirmaciones causales. El epilogismo es una inferencia que se mueve enteramente dentro del dominio de las cosas visibles y evidentes, trata de no invocar lo inobservable.

La escuela dogmática de la medicina griega antigua empleó el analogismo como método de inferencia. Este método utilizaba la analogía para razonar desde lo que se observaba hasta fuerzas no observables.

Filosofía moderna temprana

En 1620, el filósofo moderno temprano Francis Bacon repudió el valor de la mera experiencia y la inducción enumerativa por sí sola. Su método de inductivismo requería que las observaciones minuciosas y muy variadas que descubrieran la estructura del mundo natural y las relaciones causales debían combinarse con la inducción enumerativa para tener un conocimiento más allá del alcance actual de la experiencia. Por lo tanto, el inductivismo requería la inducción enumerativa como componente.

David hume

La postura del empirista David Hume de 1740 encontró que la inducción enumerativa no tenía una base racional, y mucho menos lógica; en cambio, la inducción fue producto del instinto más que de la razón, una costumbre de la mente y un requisito cotidiano para vivir. Si bien las observaciones, como el movimiento del sol, podían combinarse con el principio de la uniformidad de la naturaleza para producir conclusiones que parecían seguras, el problema de la inducción surgió del hecho de que la uniformidad de la naturaleza no era un principio lógicamente válido., por lo tanto, no podría defenderse como deductivamente racional, pero tampoco podría defenderse como inductivamente racional apelando al hecho de que la uniformidad de la naturaleza ha descrito con precisión el pasado y, por lo tanto,

Desde que Hume escribió por primera vez sobre el dilema entre la invalidez de los argumentos deductivos y la circularidad de los argumentos inductivos en apoyo de la uniformidad de la naturaleza, esta supuesta dicotomía entre meramente dos modos de inferencia, deducción e inducción, ha sido cuestionada con el descubrimiento de un tercer modo de inferencia conocido como abducción, o razonamiento abductivo, que fue formulado y propuesto por primera vez por Charles Sanders Peirce, en 1886, donde se refirió a él como "razonamiento por hipótesis". La inferencia a la mejor explicación a menudo se considera sinónimo de abducción, ya que Gilbert Harman la identificó por primera vez en 1965, donde se refirió a ella como "razonamiento abductivo", pero su definición de abducción difiere ligeramente de la definición de Pierce. Independientemente, si la abducción es de hecho un tercer modo de inferencia racionalmente independiente de los otros dos, entonces la uniformidad de la naturaleza puede justificarse racionalmente a través de la abducción, o el dilema de Hume es más un trilema. Hume también se mostró escéptico ante la aplicación de la inducción enumerativa y la razón para llegar a la certeza sobre los inobservables y especialmente la inferencia de causalidad a partir del hecho de que la modificación de un aspecto de una relación impide o produce un resultado particular.

Immanuel Kant

Despertado del "sueño dogmático" por una traducción al alemán de la obra de Hume, Kant trató de explicar la posibilidad de la metafísica. En 1781, la Crítica de la razón pura de Kant introdujo el racionalismo como un camino hacia el conocimiento distinto del empirismo. Kant clasificó las declaraciones en dos tipos. Los enunciados analíticos son verdaderos en virtud de la disposición de sus términos y significados, por lo que los enunciados analíticos son tautologías, meras verdades lógicas, verdaderas por necesidad. Mientras que las declaraciones sintéticas tienen significados para referirse a estados de hechos, contingencias. Tanto contra filósofos racionalistas como Descartes y Leibniz como contra filósofos empiristas como Locke y Hume, la Crítica de la razón pura de Kantes un argumento sostenido de que para tener conocimiento necesitamos tanto una contribución de nuestra mente (conceptos) como una contribución de nuestros sentidos (intuiciones). El conocimiento propiamente dicho está para Kant restringido a lo que posiblemente podamos percibir (fenómenos), mientras que los objetos del mero pensamiento ("cosas en sí mismas") son en principio incognoscibles debido a la imposibilidad de percibirlos alguna vez.

Razonando que la mente debe contener sus propias categorías para organizar los datos de los sentidos, haciendo posible la experiencia de los objetos en el espacio y el tiempo (fenómenos), Kant concluyó que la uniformidad de la naturaleza era una verdad a priori. Una clase de enunciados sintéticos que no era contingente sino verdadero por necesidad, era entonces sintético a priori. Kant salvó así tanto la metafísica como la ley de gravitación universal de Newton. Sobre la base del argumento de que lo que va más allá de nuestro conocimiento es "nada para nosotros",descartó el realismo científico. La posición de Kant de que el conocimiento se produce por una cooperación de la percepción y nuestra capacidad de pensar (idealismo trascendental) dio origen al movimiento del idealismo alemán. Posteriormente, el idealismo absoluto de Hegel floreció en toda Europa continental e Inglaterra.

Filosofía moderna tardía

El positivismo, desarrollado por Saint-Simon y promulgado en la década de 1830 por su antiguo alumno Comte, fue la primera filosofía de la ciencia de la modernidad tardía. Después de la Revolución Francesa, temiendo la ruina de la sociedad, Comte se opuso a la metafísica. El conocimiento humano había evolucionado de la religión a la metafísica a la ciencia, dijo Comte, que había fluido de las matemáticas a la astronomía a la física a la química a la biología a la sociología, en ese orden, describiendo dominios cada vez más intrincados. Todo el conocimiento de la sociedad se había vuelto científico, siendo incontestables las cuestiones de teología y de metafísica. Comte encontró confiable la inducción enumerativa como consecuencia de su base en la experiencia disponible. Afirmó el uso de la ciencia, en lugar de la verdad metafísica, como el método correcto para la mejora de la sociedad humana.

Según Comte, el método científico enmarca las predicciones, las confirma y enuncia leyes —enunciados positivos— irrefutables por la teología o la metafísica. En cuanto a la experiencia como una justificación de la inducción enumerativa al demostrar la uniformidad de la naturaleza, el filósofo británico John Stuart Mill acogió con beneplácito el positivismo de Comte, pero pensó que las leyes científicas eran susceptibles de ser revocadas o revisadas y Mill también se abstuvo de participar en La religión de la humanidad de Comte. Comte confiaba en tratar la ley científica como una base irrefutable para todo conocimiento, y creía que las iglesias, honrando a los científicos eminentes, deberían enfocar la mentalidad pública en el altruismo —un término acuñado por Comte— para aplicar la ciencia al bienestar social de la humanidad a través de la sociología, la ciencia principal de Comte..

Durante las décadas de 1830 y 1840, mientras Comte y Mill eran los principales filósofos de la ciencia, William Whewell encontró que la inducción enumerativa no era tan convincente y, a pesar del dominio del inductivismo, formuló la "superinducción". Whewell argumentó que " debe reconocerse la importancia peculiar del término Inducción ": "hay alguna Concepción superpuesta a los hechos", es decir, "la Invención de una nueva Concepción en cada inferencia inductiva". La creación de Conceptions se pasa por alto fácilmente y antes de Whewell rara vez se reconocía. Whewell explicó:

"Aunque vinculamos los hechos superponiendo sobre ellos un nuevo Concepto, este Concepto, una vez introducido y aplicado, se considera inseparablemente conectado con los hechos, y necesariamente implicado en ellos. Una vez que los fenómenos se unieron en sus mentes en virtud de la Concepción, los hombres ya no pueden restaurarlos fácilmente a la condición separada e incoherente en la que se encontraban antes de que fueran así combinados".

Estas explicaciones "superinducidas" bien pueden ser defectuosas, pero su precisión se sugiere cuando exhiben lo que Whewell denominó consilience, es decir, predicen simultáneamente las generalizaciones inductivas en múltiples áreas, una hazaña que, según Whewell, puede establecer su verdad. Quizás para adaptarse a la visión predominante de la ciencia como método inductivista, Whewell dedicó varios capítulos a los "métodos de inducción" y, en ocasiones, usó la frase "lógica de la inducción", a pesar de que la inducción carece de reglas y no se puede entrenar.

En la década de 1870, el creador del pragmatismo, CS Peirce, realizó vastas investigaciones que clarificaron la base de la inferencia deductiva como prueba matemática (al igual que Gottlob Frege, de manera independiente). Peirce reconoció la inducción pero siempre insistió en un tercer tipo de inferencia que Peirce denominó abducción o retroducción o hipótesis o presunción. Filósofos posteriores denominaron a la abducción de Peirce, etc., Inferencia a la Mejor Explicación (IBE).

Filosofía contemporánea

Bertrand Russell

Habiendo resaltado el problema de la inducción de Hume, John Maynard Keynes planteó la probabilidad lógica como su respuesta, o la solución más cercana a la que pudo llegar. Bertrand Russell encontró en el Tratado de Probabilidad de Keynes el mejor examen de la inducción, y creía que si se leía con Le Probleme logique de l'induction de Jean Nicod, así como con la revisión de RB Braithwaite del trabajo de Keynes en el número de octubre de 1925 de Mind, eso cubriría "la mayoría de de lo que se sabe sobre inducción", aunque el "tema es técnico y difícil, con mucha matemática". Dos décadas después, Russell propuso la inducción enumerativa como un "principio lógico independiente". Russell encontró:

"El escepticismo de Hume se basa enteramente en su rechazo del principio de inducción. El principio de inducción, aplicado a la causalidad, dice que, si A se ha encontrado muy a menudo acompañada o seguida por B, entonces es probable que en la próxima ocasión en que se observa A, será acompañado o seguido por B. Para que el principio sea adecuado, un número suficiente de instancias debe hacer que la probabilidad no esté lejos de la certeza. Si este principio, o cualquier otro del que pueda deducirse, es verdadero, entonces las inferencias casuales que Hume rechaza son válidas, no por dar certeza, sino por dar una probabilidad suficiente para fines prácticos. Si este principio no es cierto, todo intento de llegar a leyes científicas generales a partir de observaciones particulares es falaz, y el escepticismo de Hume es ineludible para un empirista. Por supuesto, el principio mismo no puede inferirse sin circularidad a partir de las uniformidades observadas, ya que se requiere para justificar tal inferencia. Por tanto, debe ser, o deducirse de, un principio independiente no basado en la experiencia. En esta medida, Hume ha demostrado que el empirismo puro no es una base suficiente para la ciencia. Pero si se admite este principio, todo lo demás puede proceder de acuerdo con la teoría de que todo nuestro conocimiento se basa en la experiencia. Debe admitirse que esto es una seria desviación del empirismo puro, y que aquellos que no son empiristas pueden preguntarse por qué, si se permite una desviación, otras están prohibidas. Estas, sin embargo, no son preguntas planteadas directamente por los argumentos de Hume. Lo que prueban estos argumentos, y no creo que la prueba pueda ser controvertida, es que la inducción es un principio lógico independiente, incapaz de ser inferido ni de la experiencia ni de otros principios lógicos, y que sin este principio, la ciencia es imposible". todo lo demás puede proceder de acuerdo con la teoría de que todo nuestro conocimiento se basa en la experiencia. Debe admitirse que esto es una seria desviación del empirismo puro, y que aquellos que no son empiristas pueden preguntarse por qué, si se permite una desviación, otras están prohibidas. Estas, sin embargo, no son preguntas planteadas directamente por los argumentos de Hume. Lo que prueban estos argumentos, y no creo que la prueba pueda ser controvertida, es que la inducción es un principio lógico independiente, incapaz de ser inferido ni de la experiencia ni de otros principios lógicos, y que sin este principio, la ciencia es imposible". todo lo demás puede proceder de acuerdo con la teoría de que todo nuestro conocimiento se basa en la experiencia. Debe admitirse que esto es una seria desviación del empirismo puro, y que aquellos que no son empiristas pueden preguntarse por qué, si se permite una desviación, otras están prohibidas. Estas, sin embargo, no son preguntas planteadas directamente por los argumentos de Hume. Lo que prueban estos argumentos, y no creo que la prueba pueda ser controvertida, es que la inducción es un principio lógico independiente, incapaz de ser inferido ni de la experiencia ni de otros principios lógicos, y que sin este principio, la ciencia es imposible". otros están prohibidos. Estas, sin embargo, no son preguntas planteadas directamente por los argumentos de Hume. Lo que prueban estos argumentos, y no creo que la prueba pueda ser controvertida, es que la inducción es un principio lógico independiente, incapaz de ser inferido ni de la experiencia ni de otros principios lógicos, y que sin este principio, la ciencia es imposible". otros están prohibidos. Estas, sin embargo, no son preguntas planteadas directamente por los argumentos de Hume. Lo que prueban estos argumentos, y no creo que la prueba pueda ser controvertida, es que la inducción es un principio lógico independiente, incapaz de ser inferido ni de la experiencia ni de otros principios lógicos, y que sin este principio, la ciencia es imposible".

Gilberto Harman

En un artículo de 1965, Gilbert Harman explicó que la inducción enumerativa no es un fenómeno autónomo, sino simplemente una consecuencia encubierta de la Inferencia a la mejor explicación (IBE). IBE es, por lo demás, sinónimo del secuestro de CS Peirce. Muchos filósofos de la ciencia que defienden el realismo científico han sostenido que la EIB es la forma en que los científicos desarrollan teorías científicas aproximadamente verdaderas sobre la naturaleza.

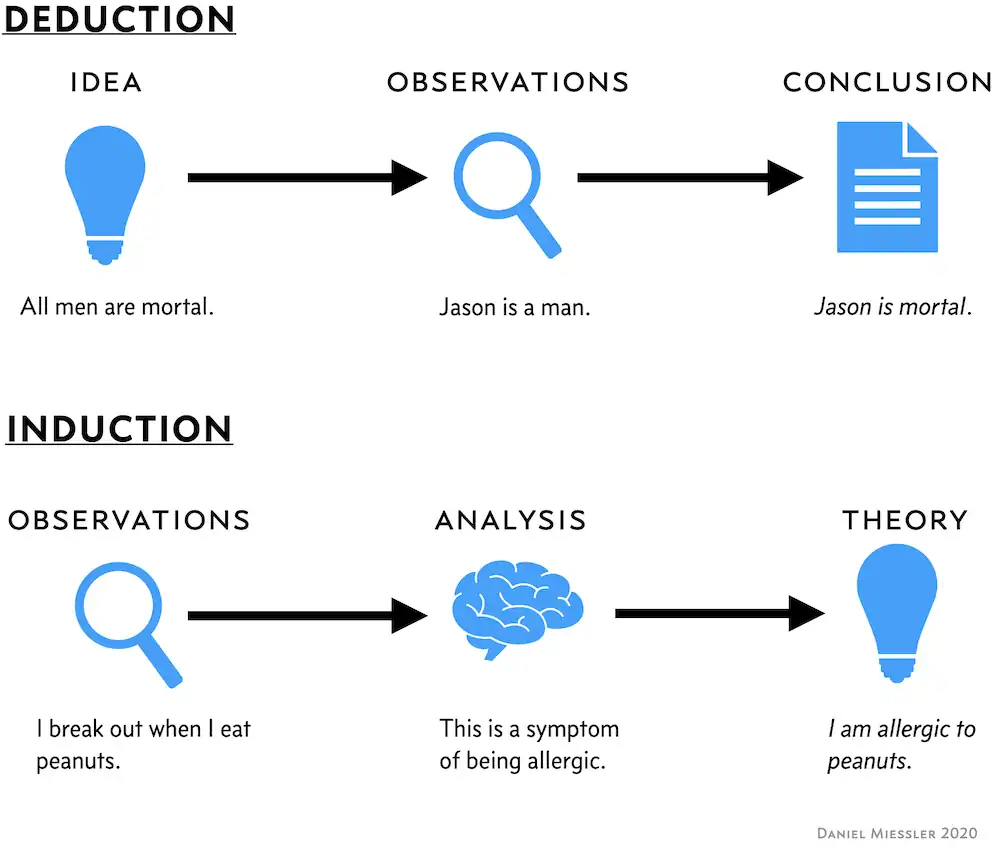
Comparación con el razonamiento deductivo

El razonamiento inductivo es una forma de argumento que, a diferencia del razonamiento deductivo, admite la posibilidad de que una conclusión sea falsa, incluso si todas las premisas son verdaderas. Esta diferencia entre el razonamiento deductivo e inductivo se refleja en la terminología utilizada para describir los argumentos deductivos e inductivos. En el razonamiento deductivo, un argumento es "válido" cuando, asumiendo que las premisas del argumento son verdaderas, la conclusión debe ser verdadera. Si el argumento es válido y las premisas son verdaderas, entonces el argumento es "sólido". Por el contrario, en el razonamiento inductivo, las premisas de un argumento nunca pueden garantizar que la conclusión debeser cierto; por lo tanto, los argumentos inductivos nunca pueden ser válidos o sólidos. En cambio, un argumento es "fuerte" cuando, asumiendo que las premisas del argumento son verdaderas, la conclusión es probablemente verdadera. Si el argumento es fuerte y las premisas son verdaderas, entonces el argumento es "convincente". Menos formalmente, un argumento inductivo puede llamarse "probable", "plausible", "probable", "razonable" o "justificado", pero nunca "seguro" o "necesario". La lógica no ofrece ningún puente de lo probable a lo cierto.

La futilidad de obtener certeza a través de alguna masa crítica de probabilidad puede ilustrarse con un ejercicio de tirar una moneda. Supongamos que alguien prueba si una moneda es justa de una o dos caras. Lanzan la moneda diez veces y diez veces sale cara. En este punto, hay una fuerte razón para creer que tiene dos cabezas. Después de todo, la posibilidad de que salgan diez caras seguidas es 0,000976: menos de una entre mil. Luego, después de 100 lanzamientos, todos los lanzamientos han salido cara. Ahora existe la certeza “virtual” de que la moneda tiene dos cabezas. Aún así, uno no puede ni lógica ni empíricamente descartar que el siguiente lanzamiento produzca cruces. No importa cuántas veces seguidas salga cara, este sigue siendo el caso. Si programamos una máquina para lanzar una moneda una y otra vez continuamente en algún momento, el resultado sería una cadena de 100 caras. En la plenitud de los tiempos,

En cuanto a la escasa posibilidad de obtener diez de cada diez caras de una moneda justa, el resultado que hizo que la moneda pareciera sesgada, muchos pueden sorprenderse al saber que la posibilidad de cualquier secuencia de caras o cruces es igualmente improbable (por ejemplo, HHTTHTHHHT) y, sin embargo, ocurre en cada prueba de diez lanzamientos. Eso significa que todos los resultados de diez lanzamientos tienen la misma probabilidad de obtener diez de diez caras, que es 0,000976. Si uno registra las secuencias de cara y cruz, para cualquier resultado, esa secuencia exacta tenía una probabilidad de 0.000976.

Un argumento es deductivo cuando la conclusión es necesaria dadas las premisas. Es decir, la conclusión debe ser verdadera si las premisas son verdaderas.

Si una conclusión deductiva se sigue debidamente de sus premisas, entonces es válida; de lo contrario, no es válido (que un argumento no sea válido no quiere decir que sea falso; puede tener una conclusión verdadera, pero no a causa de las premisas). Un examen de los siguientes ejemplos mostrará que la relación entre las premisas y la conclusión es tal que la verdad de la conclusión ya está implícita en las premisas. Los solteros no están casados ​​porque decimosellos son; los hemos definido así. Sócrates es mortal porque lo hemos incluido en un conjunto de seres que son mortales. La conclusión de un argumento deductivo válido ya está contenida en las premisas ya que su verdad es estrictamente una cuestión de relaciones lógicas. No puede decir más que sus premisas. Las premisas inductivas, por otro lado, extraen su sustancia de los hechos y la evidencia, y la conclusión, en consecuencia, hace una afirmación o predicción fáctica. Su fiabilidad varía proporcionalmente con la evidencia. La inducción quiere revelar algo nuevo sobre el mundo. Se podría decir que la inducción quiere decir más de lo que está contenido en las premisas.

Para ver mejor la diferencia entre argumentos inductivos y deductivos, considera que no tendría sentido decir: "todos los rectángulos examinados hasta ahora tienen cuatro ángulos rectos, por lo que el siguiente que veo tendrá cuatro ángulos rectos". Esto trataría las relaciones lógicas como algo fáctico y detectable y, por lo tanto, variable e incierto. Del mismo modo, hablando deductivamente podemos decir permisiblemente. "Todos los unicornios pueden volar; tengo un unicornio llamado Charlie; por lo tanto, Charlie puede volar". Este argumento deductivo es válido porque se mantienen las relaciones lógicas; no estamos interesados ​​en su solidez fáctica.

El razonamiento inductivo es inherentemente incierto. Solo se ocupa de la medida en que, dadas las premisas, la conclusión es creíble de acuerdo con alguna teoría de la evidencia. Los ejemplos incluyen una lógica de muchos valores, la teoría de Dempster-Shafer o la teoría de la probabilidad con reglas para la inferencia como la regla de Bayes. A diferencia del razonamiento deductivo, no se basa en universales que se mantengan en un dominio cerrado del discurso para sacar conclusiones, por lo que puede ser aplicable incluso en casos de incertidumbre epistémica (sin embargo, pueden surgir problemas técnicos con esto; por ejemplo, el segundo axioma de probabilidad es una suposición de mundo cerrado).

Otra diferencia crucial entre estos dos tipos de argumentos es que la certeza deductiva es imposible en sistemas no axiomáticos como la realidad, dejando el razonamiento inductivo como la ruta principal hacia el conocimiento (probabilístico) de tales sistemas.

Dado que "si A es verdadero, eso haría que B, C y D sean verdaderos", un ejemplo de deducción sería " A es verdadero, por lo tanto, podemos deducir que B, C y D son verdaderos". Un ejemplo de inducción sería " Se observa que B, C y D son verdaderos, por lo tanto, A podría ser verdadero". A es una explicación razonable para que B, C y D sean verdaderas.

Por ejemplo:El impacto de un asteroide lo suficientemente grande crearía un cráter muy grande y causaría un invierno de impacto severo que podría llevar a los dinosaurios no aviares a la extinción.Observamos que hay un cráter muy grande en el Golfo de México que data de una época muy cercana a la extinción de los dinosaurios no aviares.Por lo tanto, es posible que este impacto pueda explicar por qué los dinosaurios no aviares se extinguieron.

Tenga en cuenta, sin embargo, que la explicación del asteroide para la extinción masiva no es necesariamente correcta. Otros eventos con el potencial de afectar el clima global también coinciden con la extinción de los dinosaurios no aviares. Por ejemplo, la liberación de gases volcánicos (particularmente dióxido de azufre) durante la formación de las Trampas Deccan en India.

Otro ejemplo de un argumento inductivo:Todas las formas de vida biológica que conocemos dependen del agua líquida para existir.Por lo tanto, si descubrimos una nueva forma de vida biológica, probablemente dependerá del agua líquida para existir.

Este argumento podría haberse hecho cada vez que se encontraba una nueva forma de vida biológica, y habría sido correcto en todas las ocasiones; sin embargo, todavía es posible que en el futuro se descubra una forma de vida biológica que no requiera agua líquida. Como resultado, el argumento puede formularse de manera menos formal como:Todas las formas de vida biológica que conocemos dependen del agua líquida para existir.Por lo tanto, toda la vida biológica probablemente depende del agua líquida para existir.

John Vickers presentó un ejemplo clásico de un argumento inductivo incorrecto:Todos los cisnes que hemos visto son blancos.Por lo tanto, sabemos que todos los cisnes son blancos.

La conclusión correcta sería: esperamos que todos los cisnes sean blancos.

En pocas palabras: la deducción se trata de certeza/necesidad; la inducción se trata de probabilidad. Cualquier afirmación individual responderá a uno de estos dos criterios. Otro enfoque para el análisis del razonamiento es el de la lógica modal, que se ocupa de la distinción entre lo necesario y lo posible sin preocuparse por las probabilidades entre las cosas que se consideran posibles.

La definición filosófica del razonamiento inductivo tiene más matices que una simple progresión de instancias particulares/individuales a generalizaciones más amplias. Más bien, las premisas de un argumento lógico inductivo indican cierto grado de apoyo (probabilidad inductiva) para la conclusión pero no la implican; es decir, sugieren la verdad pero no la aseguran. De esta manera, existe la posibilidad de pasar de enunciados generales a instancias individuales (por ejemplo, silogismos estadísticos).

Tenga en cuenta que la definición de razonamiento inductivo descrita aquí difiere de la inducción matemática, que, de hecho, es una forma de razonamiento deductivo. La inducción matemática se utiliza para proporcionar pruebas estrictas de las propiedades de los conjuntos definidos recursivamente. La naturaleza deductiva de la inducción matemática se deriva de su base en un número no finito de casos, en contraste con el número finito de casos involucrados en un procedimiento de inducción enumerativa como prueba por agotamiento. Tanto la inducción matemática como la prueba por agotamiento son ejemplos de inducción completa. La inducción completa es un tipo enmascarado de razonamiento deductivo.

Crítica

Aunque los filósofos, al menos desde el filósofo pirronista Sextus Empiricus, han señalado la falta de solidez del razonamiento inductivo, la crítica filosófica clásica del problema de la inducción fue realizada por el filósofo escocés David Hume.Aunque el uso del razonamiento inductivo demuestra un éxito considerable, la justificación de su aplicación ha sido cuestionable. Al reconocer esto, Hume destacó el hecho de que nuestra mente a menudo saca conclusiones de experiencias relativamente limitadas que parecen correctas pero que en realidad están lejos de ser ciertas. En la deducción, el valor de verdad de la conclusión se basa en la verdad de la premisa. En la inducción, sin embargo, la dependencia de la conclusión de la premisa siempre es incierta. Por ejemplo, supongamos que todos los cuervos son negros. El hecho de que haya numerosos cuervos negros apoya la suposición. Nuestra suposición, sin embargo, se vuelve inválida una vez que se descubre que hay cuervos blancos. Por lo tanto, la regla general "todos los cuervos son negros" no es el tipo de declaración que pueda ser cierta. Hume argumentó además que es imposible justificar el razonamiento inductivo: esto se debe a que no se puede justificar deductivamente, por lo que nuestra única opción es justificarlo inductivamente. Dado que este argumento es circular, con la ayuda del tenedor de Hume concluyó que nuestro uso de la inducción es injustificable.

Sin embargo, Hume afirmó que incluso si se demostrara que la inducción no es confiable, todavía tendríamos que confiar en ella. Entonces, en lugar de una posición de escepticismo severo, Hume abogó por un escepticismo práctico basado en el sentido común, donde se acepta la inevitabilidad de la inducción. Bertrand Russell ilustró el escepticismo de Hume en una historia sobre un pollo, alimentado todas las mañanas sin falta, que siguiendo las leyes de inducción concluyó que esta alimentación siempre continuaría, hasta que el granjero finalmente le cortó la garganta.

En 1963, Karl Popper escribió: "La inducción, es decir, la inferencia basada en muchas observaciones, es un mito. No es un hecho psicológico, ni un hecho de la vida ordinaria, ni un hecho de procedimiento científico". El libro de Popper de 1972, Conocimiento objetivo, cuyo primer capítulo está dedicado al problema de la inducción, comienza así: "Creo que he resuelto un problema filosófico importante: el problema de la inducción". En el esquema de Popper, la inducción enumerativa es "una especie de ilusión óptica" proyectada por los pasos de conjetura y refutación durante un cambio de problema. Un salto imaginativo, la solución tentativa es improvisada, careciendo de reglas inductivas que la guíen. La generalización resultante, sin restricciones, es deductiva, una consecuencia implícita de todas las consideraciones explicativas. Sin embargo, la controversia continuó y la supuesta solución de Popper no fue aceptada en general.

Donald Gillies argumenta que las reglas de las inferencias relacionadas con el razonamiento inductivo están abrumadoramente ausentes de la ciencia, y describe la mayoría de las inferencias científicas como "involucrando conjeturas pensadas por el ingenio y la creatividad humanos, y de ninguna manera inferidas de manera mecánica, o de acuerdo con reglas especificadas con precisión”. Gillies también ofrece un raro contraejemplo "en los programas de aprendizaje automático de IA".

Sesgos

El razonamiento inductivo también se conoce como construcción de hipótesis porque las conclusiones que se obtienen se basan en el conocimiento y las predicciones actuales. Al igual que con los argumentos deductivos, los sesgos pueden distorsionar la aplicación adecuada del argumento inductivo, lo que impide que el razonador forme la conclusión más lógica basada en las pistas. Ejemplos de estos sesgos incluyen la heurística de disponibilidad, el sesgo de confirmación y el sesgo del mundo predecible.

La heurística de disponibilidad hace que el razonador dependa principalmente de la información que está fácilmente disponible para él o ella. Las personas tienden a confiar en la información que es fácilmente accesible en el mundo que les rodea. Por ejemplo, en las encuestas, cuando se les pide a las personas que calculen el porcentaje de personas que murieron por diversas causas, la mayoría de los encuestados eligen las causas que han prevalecido en los medios, como terrorismo, asesinatos y accidentes aéreos, en lugar de causas como enfermedades y accidentes de tráfico, que técnicamente han sido "menos accesibles" para el individuo ya que no se enfatizan tanto en el mundo que lo rodea.

El sesgo de confirmación se basa en la tendencia natural a confirmar en lugar de negar una hipótesis actual. La investigación ha demostrado que las personas tienden a buscar soluciones a los problemas que son más consistentes con las hipótesis conocidas en lugar de intentar refutar esas hipótesis. A menudo, en los experimentos, los sujetos harán preguntas que buscan respuestas que se ajusten a las hipótesis establecidas, confirmando así estas hipótesis. Por ejemplo, si se plantea la hipótesis de que Sally es una persona sociable, los sujetos buscarán naturalmente confirmar la premisa haciendo preguntas que produzcan respuestas que confirmen que Sally es, de hecho, una persona sociable.

El sesgo del mundo predecible gira en torno a la inclinación a percibir el orden donde no se ha demostrado que exista, ya sea en absoluto o en un nivel particular de abstracción. El juego, por ejemplo, es uno de los ejemplos más populares del sesgo del mundo predecible. Los jugadores a menudo comienzan a pensar que ven patrones simples y obvios en los resultados y, por lo tanto, creen que pueden predecir los resultados en función de lo que han presenciado. En realidad, sin embargo, los resultados de estos juegos son difíciles de predecir y de naturaleza muy compleja. En general, las personas tienden a buscar algún tipo de orden simplista para explicar o justificar sus creencias y experiencias, y a menudo les resulta difícil darse cuenta de que sus percepciones del orden pueden ser completamente diferentes de la verdad.

Inferencia bayesiana

Como una lógica de inducción en lugar de una teoría de la creencia, la inferencia bayesiana no determina qué creencias son racionales a priori, sino que determina cómo debemos cambiar racionalmente las creencias que tenemos cuando se nos presentan pruebas. Comenzamos comprometiéndonos con una probabilidad previa para una hipótesis basada en la lógica o la experiencia previa y, cuando nos enfrentamos a la evidencia, ajustamos la fuerza de nuestra creencia en esa hipótesis de manera precisa utilizando la lógica bayesiana.

Inferencia inductiva

Alrededor de 1960, Ray Solomonoff fundó la teoría de la inferencia inductiva universal, una teoría de predicción basada en observaciones, por ejemplo, predecir el siguiente símbolo en función de una serie dada de símbolos. Este es un marco inductivo formal que combina la teoría algorítmica de la información con el marco bayesiano. La inferencia inductiva universal se basa en sólidos fundamentos filosóficos y puede considerarse como una navaja de Occam matemáticamente formalizada. Los ingredientes fundamentales de la teoría son los conceptos de probabilidad algorítmica y complejidad de Kolmogorov.