Radio de giro
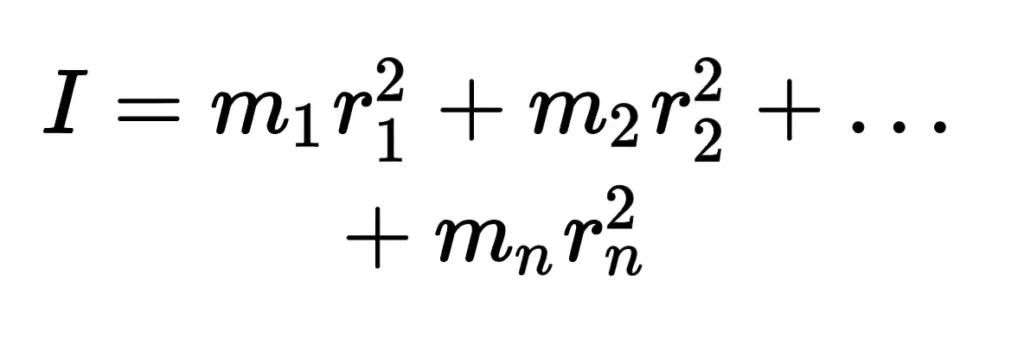
m = masa
r = distancias perpendiculares desde el eje de rotación
El radio de giro es la distancia desde el eje de rotación hasta un punto radial hipotético donde el momento de inercia sería igual, si toda la masa estuviera concentrada en ese punto. Asumiendo al eje de rotación como el centro de masa de cuerpo y el momento inercial sobre la distribución real de la masa del cuerpo. El radio de giro se denomina a veces radio de inercia.
Matemáticamente, el radio de giro se define como la raíz cuadrada de la distancia media cuadrática de todas las partes del objeto desde su centro de masa o un eje específico. Esencialmente, representa la distancia perpendicular desde una masa puntual imaginaria hasta el eje de rotación. Este concepto permite visualizar la trayectoria de un punto en movimiento en un cuerpo, proporcionando una medida de la distancia típica que recorre este punto.
El radio de giro permite entender cómo se distribuye la masa de un objeto en relación a su rotación, y más específicamente cómo la distribución de la masa afecta la forma en que un objeto gira.
Para calcular el radio de giro de un cuerpo compuesto por 'n' partículas, cada una con una masa 'm', se consideran sus distancias perpendiculares 'r1, r2, r3, ..., rn' al eje de rotación. El momento de inercia 'I' del cuerpo respecto a este eje se expresa como la suma de los productos de la masa de cada partícula por el cuadrado de su distancia al eje. En el caso de que todas las masas sean iguales, el momento de inercia se simplifica a 'I = m(r1² + r2² + ... + rn²)'. Si 'M' es la masa total del cuerpo y 'm = M/n', entonces 'I = M(r1² + r2² + ... + rn²)/n'.
- I=m1r12+m2r22+⋯ ⋯ +mnrn2{displaystyle I=m_{1}r_{2}+m_{2}r_{2}{2}+cdots ¿Qué?
Desde donde es la masa total del cuerpo,
- I=M()r12+r22+⋯ ⋯ +rn2)/n{displaystyle I=M(r_{1}{2}+r_{2}{2}+cdots ¿Qué?
De las ecuaciones anteriores, tenemos
- MRg2=M()r12+r22+⋯ ⋯ +rn2)/n{displaystyle MR_{g}{2}=M(r_{1}{2}+r_{2}{2}+cdots ¿Qué?
El radio de giro es la raíz de la distancia cuadrática media de las partículas desde la fórmula del eje
- Rg2=()r12+r22+⋯ ⋯ +rn2)/n{displaystyle R_{2}{2}=(r_{1}{2}+r_{2}{2}+cdots ¿Qué?
De estas ecuaciones, se deduce que el cuadrado del radio de giro 'Rg²' es igual a la media cuadrática de las distancias de las partículas al eje, es decir, 'Rg² = (r1² + r2² + ... + rn²)/n'. Por lo tanto, el radio de giro de un cuerpo alrededor de un eje dado también puede definirse como la raíz cuadrada de esta media cuadrática, proporcionando una medida de cómo se distribuye la masa del cuerpo giratorio alrededor de su eje.
En la ciencia de polímeros, según la definición de la Unión Internacional de Física Pura y Aplicada (IUPAP), el radio de giro se refiere a la raíz cuadrada del promedio ponderado de las distancias al cuadrado de 'n' elementos de masa de una macromolécula desde su centro de masa. Estos elementos de masa suelen ser los grupos esqueléticos que constituyen la macromolécula, como el grupo –CH2– en el poli(metileno). El radio de giro es una herramienta crucial para entender la distribución de la masa en cuerpos rotatorios y macromoléculas.
HSD
Aplicaciones en ingeniería estructural
En ingeniería estructural, el radio de giro bidimensional se usa para describir la distribución del área de la sección transversal en una columna alrededor de su eje centroidal con la masa del cuerpo. El radio de giro viene dado por la siguiente fórmula:
- Rg2=IA{displaystyle R_{mathrm {g} }{2}={frac {I}{A}}
o
- Rg=IA{displaystyle ¿Qué? {} {}}}}
Donde I{displaystyle Yo... es el segundo momento de la zona y A{displaystyle A} es el área transversal total.
El radio de giro es útil para estimar la rigidez de una columna. Si los momentos principales del tensor de giro bidimensional no son iguales, la columna tenderá a pandearse alrededor del eje con el momento principal más pequeño. Por ejemplo, una columna con una sección transversal elíptica tenderá a pandearse en la dirección del semieje más pequeño.
En ingeniería, donde los cuerpos continuos de materia son generalmente los objetos de estudio, el radio de giro generalmente se calcula como una integral.
Aplicaciones en mecánica
El radio de giro sobre un eje dado (rgaxis{displaystyle r_{mathrm {}} {text{ axis}}} {f}}}}) se puede calcular en términos del momento de masa de la inercia Iaxis{displaystyle Yo... alrededor de ese eje, y la masa total m;
- rgaxis2=Iaxism{displaystyle r_{mathrm {} {text{ axis}}{2}={frac} {I_{text{axis}} {m}}} {f}} {f}} {f}}}} {f}}}} {f}}}}}}} {f}}}}}}}}} {f}}}}}} {}}}} {}}}}} {}}}}}}}} {}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}
o
- rgaxis=Iaxism{displaystyle r_{mathrm} {text{ axis}={sqrt {frac} {I_{text{axis}} {m}}}} {f}} {f}}} {f}}}}}} {}}}}} {f}}} {f}}}}} {}}}}}}}} {}}}}} {}}}}}} {}}}}}} {}}}}}}}}}}}}} {}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
Iaxis{displaystyle Yo... es un escalar, y no es el momento de la inercia tensor.
Aplicaciones en física molecular
En física de polímeros, el radio de giro se usa para describir las dimensiones de una cadena de polímero. El radio de giro de una molécula en particular en un momento dado se define como:
- Rg2=def1N.. k=1NSilenciork− − rmeanSilencio2{displaystyle ¿Qué? {fnK} {fnK}}} {fnMicroc {1} {fnK}}} {fnMicroc {fn} {fn} {fn} {fn}}} {fn}fn}}}}}}}} {fnK}}}}}}}}} {fn}fnK}}}}}}}f}}}}}}}}}}}}}}}}}}}} {s}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}s}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {s}}}s}}}}}}}}}}}}}}}}}}}s}}}}}}}}}}}}}}}}}}}}} ¿Por qué? } 'justo en la vida {2}
Donde rmean{displaystyle mathbf {r} _{mathrm {mean}} es la posición media de los monómeros.
Como se detalla a continuación, el radio de giro también es proporcional a la distancia cuadrada de la raíz media entre los monómeros:
- Rg2=def12N2.. i,jSilenciori− − rjSilencio2{displaystyle ¿Qué? {fnK} {f}}fnh} {fn} {fn}}}}}}}sum} {fn}} {fn}} {fn}} {fn} {fn}} {fn}}}}}}}}}}}}}}}}}}}}}} {f}}}}} {f} {f} {f}}f}}}}}}f}f}}f}}}}}}}}f} {f} {f} {f} {fn}}}f}f}}}}}}}}}f}}}}fnfnfnf}}}}}}}}}f}} {fnf}f}f}}}}f}}}}}}}}}fnf}}}f}}}}}}}}}}}}}}}} ¿Por qué? ¿Por qué?
Como tercer método, el radio de giro también se puede calcular sumando los momentos principales del tensor de giro.
Dado que las conformaciones de cadena de una muestra de polímero son casi infinitas en número y cambian constantemente con el tiempo, el "radio de giro" discutido en la física de polímeros generalmente debe entenderse como una media de todas las moléculas de polímero de la muestra y en el tiempo. Es decir, el radio de giro que se mide como un promedio a lo largo del tiempo o conjunto:
- Rg2=def1N... k=1NSilenciork− − rmeanSilencio2.{displaystyle ¿Qué? {fnK} {fnK}}} {fnK}langle sum ¿Por qué?....
donde los soportes angulares .. ...... .. {displaystyle langle ldots rangle } denota el promedio del conjunto.
Una cadena polimérica gobernada entrópicamente (es decir, en las llamadas condiciones theta) sigue un camino aleatorio en tres dimensiones. El radio de giro para este caso está dado por
- Rg=16Na{displaystyle ¿Qué? {sqrt {N} a}
Note que aunque aN{displaystyle aN} representa la longitud del contorno del polímero, a{displaystyle a} depende fuertemente de la rigidez del polímero y puede variar sobre órdenes de magnitud. N{displaystyle N} se reduce en consecuencia.
Una de las razones por las que el radio de giro es una propiedad interesante es que se puede determinar experimentalmente con dispersión de luz estática, así como con dispersión de rayos X y neutrones de ángulo pequeño. Esto permite a los físicos de polímeros teóricos comparar sus modelos con la realidad.
El radio hidrodinámico es numéricamente similar y se puede medir con Dynamic Light Scattering (DLS).
Derivación de la identidad
Para demostrar que las dos definiciones de Rg2{displaystyle ¿Qué? son idénticos
multiplicamos primero el summand en la primera definición:
- Rg2=def1N.. k=1N()rk− − rmean)2=1N.. k=1N[rk⋅ ⋅ rk+rmean⋅ ⋅ rmean− − 2rk⋅ ⋅ rmean]{displaystyle ¿Qué? {fnK} {fnK}}} {fn} {fn}sum _{k=1} {fn}m} {fnh} {fnh}mthbf {r} _{mhm {m}}right)}{2}={fn}} {fn}}}}}}}sum} {fn} {fn}fn}}f}}}}}}}}f}f}}f}f}}}f}}}f}}}f}fn}}}f} {f}f}fn}f}f}f}f}f}f}f}}fn}fn}fnhnhn}fn}fn}fnhn}fnhn}fn}fn}}fn}fnhnhn}}fn}}fnhnhnh}fnhn ¿Por qué? ¿Qué? }cdot mathbf {r} _{mathrm {mean} }-2mathbf {r} ¿Qué?
Llevar a cabo la suma en los dos últimos términos y utilizar la definición de rmean{displaystyle mathbf {r} _{mathrm {mean}} da la fórmula
- Rg2=def− − rmean⋅ ⋅ rmean+1N.. k=1N()rk⋅ ⋅ rk){displaystyle ¿Qué? {fnK} {fnK}}} - Mathbf. ¿Qué? }cdot mathbf {r} _{mathrm {mean} }+{frac {1}sum _{k=1} {N}left(mathbf {r} _{k}cdot mathbf {r} _{k}right)}
Aplicaciones en análisis de datos geográficos
En el análisis de datos, el radio de giro se usa para calcular muchas estadísticas diferentes, incluida la distribución de ubicaciones geográficas. Estas ubicaciones se recopilaron recientemente de los usuarios de las redes sociales para investigar las menciones típicas de un usuario. Esto puede ser útil para comprender cómo un determinado grupo de usuarios en las redes sociales utiliza la plataforma.
- Rg=.. i=1Nmi()ri− − rC)2.. i=1Nmi{displaystyle ¿Qué? ¿Por qué? ¿Qué?
Contenido relacionado
Método de Horner
Iteración
Teorema π de Buckingham
























![R_{{{mathrm {g}}}}^{{2}} {stackrel {{mathrm {def}}}{=}} {frac {1}{N}}sum _{{k=1}}^{{N}}left({mathbf {r}}_{{k}}-{mathbf {r}}_{{{mathrm {mean}}}}right)^{{2}}={frac {1}{N}}sum _{{k=1}}^{{N}}left[{mathbf {r}}_{{k}}cdot {mathbf {r}}_{{k}}+{mathbf {r}}_{{{mathrm {mean}}}}cdot {mathbf {r}}_{{{mathrm {mean}}}}-2{mathbf {r}}_{{k}}cdot {mathbf {r}}_{{{mathrm {mean}}}}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/79fe631913c6652c7f2a08bdb5eced730576b2e3)

