Teorema π de Buckingham

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

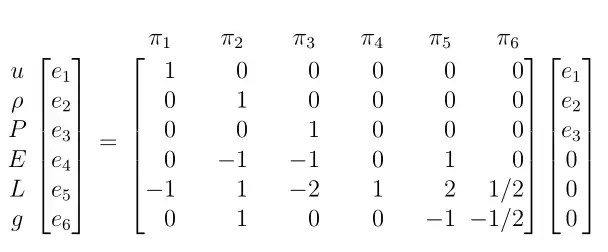
El Teorema π de Buckingham es un principio fundamental en la física que establece que cualquier ecuación físicamente significativa que involucre un número de variables puede expresarse de manera equivalente como una ecuación de un conjunto de parámetros adimensionales derivados de estas variables. Este principio es la base del análisis dimensional.

El teorema de Buckingham es ampliamente utilizado por su capacidad para simplificar fenómenos físicos complejos en relaciones adimensionales, facilitando la comprensión y el análisis de los principios subyacentes que rigen estos fenómenos. Es especialmente valioso en la física experimental y la ingeniería, donde ayuda en el diseño de experimentos, en la escala de resultados de modelos para aplicaciones en el mundo real, y en la identificación de números adimensionales clave que caracterizan diferentes situaciones físicas.

Este teorema, representa una formalización avanzada del método de análisis dimensional desarrollado inicialmente por Rayleigh y formalmente establece que:

cualquier ecuación físicamente significativa que involucre un número n de variables físicas, puede ser reescrita utilizando un conjunto de p = n − k parámetros adimensionales, denotados como π₁, π₂, ..., π_p

Estos parámetros se derivan de las variables originales, donde k representa el número de dimensiones físicas fundamentales y se determina por el rango de una matriz específica.

Una de las contribuciones clave de este teorema es la provisión de un método sistemático para la adimensionalización, es decir, para convertir un conjunto de variables dadas en parámetros adimensionales. Esto es particularmente útil en situaciones donde la forma exacta de la ecuación física aún no se conoce.

Además, el Teorema π de Buckingham demuestra el principio fundamental de la física de que las leyes físicas son consistentes y universales, independientemente del sistema de unidades empleado. Esto implica que cualquier ley física puede ser expresada mediante una relación que involucre únicamente combinaciones adimensionales de las variables concernientes. Por ejemplo, en la ley de Boyle, la relación entre presión y volumen se expresan como inversamente proporcionales. Si el valor de estas combinaciones adimensionales variara con los sistemas de unidades, entonces la ecuación no mantendría su validez universal, contradiciendo el teorema.

HSD

Historia

Aunque lleva el nombre de Edgar Buckingham, el teorema $π$ fue probado por primera vez por el matemático francés Joseph Bertrand en 1878. Bertrand consideró solo casos especiales de problemas de electrodinámica y conducción de calor, pero su artículo contiene, en distintos términos, todas las ideas básicas de la demostración moderna del teorema e indica claramente la utilidad del teorema para modelar fenómenos físicos. La técnica de usar el teorema ("el método de las dimensiones") se hizo ampliamente conocida gracias a los trabajos de Rayleigh. La primera aplicación del teorema $π$ en el caso general a la dependencia de la caída de presión en una tubería sobre los parámetros que gobiernan probablemente se remonta a 1892, una prueba heurística con el uso de expansiones en serie, a 1894.

Generalización formal de la $π$ theorem for the case of arbitrarily many quantity was given first by A. Vaschy[fr] en 1892, entonces en 1911 —aparentemente independiente— tanto por A. Federman como D. Riabouchinsky, y otra vez en 1914 por Buckingham. Fue el artículo de Buckingham que introdujo el uso del símbolo " $pi _{i}$ "para las variables sin dimensión (o parámetros), y esta es la fuente del nombre del teorema.

Declaración

Más formalmente, el número $p$ de términos dimensionales que se pueden formar es igual a la nulidad de la matriz dimensional, y $k$ es el rango. Para propósitos experimentales, diferentes sistemas que comparten la misma descripción en términos de estos números sin dimensiones son equivalentes.

En términos matemáticos, si tenemos una ecuación físicamente significativa como

{displaystyle f(q_{1},q_{2},ldotsq_{n})=0,}

${displaystyle q_{1},ldotsq_{n}}$ $n$ $k$

{displaystyle F(pi _{1},pi _{2},ldotspi _{p})=0,}

${displaystyle pi _{1},ldotspi _{p}}$ $q_{i}$ ${displaystyle p=n-k}$ Grupos de Pi

{displaystyle pi _{i}=q_{1}^{a_{1}},q_{2}^{a_{2}}cdots q_{n}^{a_{n}},}

$a_{i}$ $pi _{i}$ $ell$ ${displaystyle pgeq n-ell }$

Importancia

El teorema $π$ de Buckingham proporciona un método para calcular conjuntos de parámetros adimensionales a partir de variables dadas, incluso si la forma de la ecuación permanece desconocido. Sin embargo, la elección de parámetros adimensionales no es única; El teorema de Buckingham solo proporciona una forma de generar conjuntos de parámetros adimensionales y no indica los más 'físicamente significativos'.

Dos sistemas en los que estos parámetros coinciden se denominan similares (como ocurre con los triángulos semejantes, sólo difieren en la escala); son equivalentes a los efectos de la ecuación, y el experimentador que quiera determinar la forma de la ecuación puede elegir la más conveniente. Lo más importante es que el teorema de Buckingham describe la relación entre el número de variables y las dimensiones fundamentales.

Prueba

Para la simplicidad, se supone que el espacio de las unidades físicas fundamentales y derivadas forma un espacio vectorial sobre los números reales, con las unidades fundamentales como vectores de base, y con la multiplicación de las unidades físicas como la operación de "adicionamiento vencedor", y la elevación a los poderes como la operación de " multiplicación escalar":
representa una variable dimensional como el conjunto de exponentes necesarios para las unidades fundamentales (con un poder de cero si la unidad fundamental particular no está presente). Por ejemplo, la gravedad estándar $g$ ha unidades de ${displaystyle D/T^{2}=D^{1}T^{-2}}$ (distancia con el tiempo cuadrado), por lo que está representado como el vector ${displaystyle (1,-2)}$ con respecto a la base de las unidades fundamentales (distancia, tiempo). También podríamos exigir que los exponentes de las unidades fundamentales sean números racionales y modifiquen la prueba en consecuencia, en cuyo caso los exponentes de los grupos pi pueden ser siempre tomados como números racionales o incluso números enteros.

Reescalado de unidades

Supongamos que tenemos cantidades ${displaystyle q_{1},q_{2},dotsq_{n}}$ , donde las unidades de $q_{i}$ contener la longitud elevada al poder $c_{i}$ . Si originalmente midemos la longitud en metros pero luego cambiamos a centímetros, entonces el valor numérico de $q_{i}$ se volvería a escalar por un factor ${displaystyle 100^{c_{i}}}$ . Cualquier ley físicamente significativa debe ser invariable bajo un rescaling arbitrario de cada unidad fundamental; este es el hecho de que el pi teorema se acuesta.

Prueba formal

Dado un sistema de $n$ variables dimensionales ${displaystyle q_{1},ldotsq_{n}}$ dentro $ell$ las dimensiones fundamentales (basis) matriz dimensional es ${displaystyle ell times n}$ matriz $M$ cuyo $ell$ filas corresponden a las dimensiones fundamentales y cuya $n$ columnas son las dimensiones de las variables: las $(i,j)$ (donde) $1leq ileq ell$ y $1leq jleq n$ ) es el poder del $i$ t dimensión fundamental en la $j$ la variable.
La matriz puede interpretarse como tomando en una combinación de las cantidades variables y dando las dimensiones de la combinación en términos de las dimensiones fundamentales. Así que... ${displaystyle ell times 1}$ vector que resulta de la multiplicación

{displaystyle M{begin{bmatrix}a_{1}\vdots \a_{n}end{bmatrix}}}

{displaystyle q_{1}^{a_{1}},q_{2}^{a_{2}}cdots q_{n}^{a_{n}}}

$ell$

Si reescalamos $i$ por un factor de $alpha _{i}$ , entonces $q_{j}$ se vuelve a escalar ${displaystyle alpha _{1}^{-m_{1j}},alpha _{2}^{-m_{2j}}cdots alpha _{ell }^{-m_{ell j}}}$ , donde $m_{ij}$ es $(i,j)$ la entrada de la matriz dimensional. Para convertir esto en un problema de álgebra lineal, tomamos logaritmos (la base es irrelevante), rindiendo

{displaystyle {begin{bmatrix}log {q_{1}}\vdots \log {q_{n}}end{bmatrix}}mapsto {begin{bmatrix}log {q_{1}}\vdots \log {q_{n}}end{bmatrix}}-M^{operatorname {T} }{begin{bmatrix}log {alpha _{1}}\vdots \log {alpha _{ell }}end{bmatrix}},}

${displaystyle mathbb {R} ^{ell }}$ $mathbb {R} ^{n}$ ${displaystyle fcolon (mathbb {R} ^{+})^{n}to mathbb {R} }$ $(q_1, q_2, dots, q_n)$ ${displaystyle f(q_{1},q_{2},dotsq_{n})=0}$ $f$ ${displaystyle Fcolon mathbb {R} ^{n}/operatorname {im} {M^{operatorname {T} }}to mathbb {R} }$ ${displaystyle mathbb {R} ^{n}/operatorname {im} {M^{operatorname {T} }}}$ ${mathbb {R}}^{p}$ ${displaystyle (log {pi _{1}},log {pi _{2}},dotslog {pi _{p}})}$

Construimos un $ntimes p$ matriz $K$ cuyas columnas son la base para ${displaystyle ker {M}}$ . Nos dice cómo incrustar ${mathbb {R}}^{p}$ en $mathbb {R} ^{n}$ como el núcleo de $M$ . Es decir, tenemos una secuencia exacta

{displaystyle 0to mathbb {R} ^{p}xrightarrow { K } mathbb {R} ^{n}xrightarrow { M } mathbb {R} ^{ell }.}

Tomar transposiciones produce otra secuencia exacta

{displaystyle mathbb {R} ^{ell }xrightarrow { M^{operatorname {T} } } mathbb {R} ^{n}xrightarrow { K^{operatorname {T} } } mathbb {R} ^{p}to 0.}

El primer teorema isomorfismo produce el isomorfismo deseado, que envía el conjunto ${displaystyle v+M^{operatorname {T} }mathbb {R} ^{ell }}$ a ${displaystyle K^{operatorname {T} }v}$ . Esto corresponde a reescribir el tuple ${displaystyle (log {q_{1}},log {q_{2}},dotslog {q_{n}})}$ en los grupos pi ${displaystyle (log {pi _{1}},log {pi _{2}},dotslog {pi _{p}})}$ procedente de las columnas de $K$ .

El Sistema Internacional de Unidades define siete unidades básicas, que son el amperio, el kelvin, el segundo, el metro, el kilogramo, la candela y el mol. A veces es ventajoso introducir unidades y técnicas básicas adicionales para refinar la técnica del análisis dimensional. (Ver análisis de orientación y referencia).

Ejemplos

Velocidad

Este ejemplo es elemental pero sirve para demostrar el procedimiento.

Supongamos que un automóvil circula a 100 km/h; ¿cuanto tarda en recorrer 200 km?

Esta cuestión considera $n = 3$ variables dimensionadas: distancia $d,$ tiempo $t,$ y velocidad $v,$ y estamos buscando alguna ley de la forma ${displaystyle t=operatorname {Duration} (v,d).}$ Cualquier dos de estas variables son dimensionalmente independientes, pero las tres juntas no lo son. Así es. ${displaystyle p=n-k=3-2=1}$ cantidad sin dimensión.

La matriz dimensional es

{displaystyle M={begin{bmatrix}1&0&;;;1\0&1&-1end{bmatrix}}}

$D$ $T,$ ${displaystyle D,T,{text{ and }}V,}$ ${displaystyle (1,-1),}$ ${displaystyle V=D^{0}T^{0}V^{1},}$ ${displaystyle mathbf {v} =[0,0,1],}$ ${displaystyle V=D^{1}T^{-1}=D/T,}$ ${displaystyle Mmathbf {v} =[1,-1].}$

Para una constante sin dimensiones ${displaystyle pi =D^{a_{1}}T^{a_{2}}V^{a_{3}},}$ estamos buscando vectores ${displaystyle mathbf {a} =[a_{1},a_{2},a_{3}]}$ tal que el producto matriz-vector ${displaystyle Mmathbf {a} }$ igual al vector cero ${displaystyle [0,0].}$ En álgebra lineal, el conjunto de vectores con esta propiedad se conoce como el núcleo (o nullspace) de la matriz dimensional. En este caso particular su núcleo es unidimensional. La matriz dimensional como se escribió arriba es en forma echelon de fila reducida, por lo que se puede leer un vector de núcleo no cero a dentro de una constante multiplicativa:

{displaystyle mathbf {a} ={begin{bmatrix}-1\;;;1\;;;1\end{bmatrix}}.}

Si la matriz dimensional no se hubiera reducido ya, se podría realizar la eliminación de Gauss-Jordan en la matriz dimensional para determinar más fácilmente el núcleo. De ello se deduce que la constante adimensional, reemplazando las dimensiones por las correspondientes variables dimensionadas, puede escribirse:

{displaystyle pi =d^{-1}t^{1}v^{1}=tv/d.}

Dado que el kernel solo se define dentro de una constante multiplicativa, la constante adimensional anterior elevada a cualquier potencia arbitraria produce otra constante adimensional (equivalente).

El análisis dimensional ha proporcionado así una ecuación general que relaciona las tres variables físicas:

{displaystyle F(pi)=0,}

$C$ ${displaystyle F,}$

{displaystyle pi =C,}

${displaystyle t=operatorname {Duration} (v,d)}$

{displaystyle t=C{frac {d}{v}}.}

La relación real entre las tres variables es simplemente ${displaystyle d=vt.}$ En otras palabras, en este caso $F$ tiene una raíz físicamente relevante, y es unidad. El hecho de que sólo un valor único $C$ lo hará y que es igual a 1 no se revela por la técnica del análisis dimensional.

El péndulo simple

Deseamos determinar el período $T$ de pequeñas oscilaciones en un péndulo simple. Se supone que es una función de la longitud $L,$ la masa ${displaystyle M,}$ y la aceleración debido a la gravedad en la superficie de la Tierra ${displaystyle g,}$ que tiene dimensiones de longitud divididas por el tiempo cuadrado. El modelo es de la forma

{displaystyle f(T,M,L,g)=0.}

(Nota que está escrito como una relación, no como una función: $T$ no está escrito aquí como una función ${displaystyle M,L,{text{ and }}g.}$ )

El período, la masa y la longitud son dimensionalmente independientes, pero la aceleración se puede expresar en términos de tiempo y longitud, lo que significa que las cuatro variables tomadas juntos no son dimensionalmente independientes. Así sólo necesitamos ${displaystyle p=n-k=4-3=1}$ parámetro sin dimensión, denotado por $pi,$ y el modelo puede ser reexpresado como

{displaystyle F(pi)=0,}

$pi$

{displaystyle pi =T^{a_{1}}M^{a_{2}}L^{a_{3}}g^{a_{4}}}

${displaystyle a_{1},a_{2},a_{3},a_{4}.}$

Las dimensiones de las cantidades dimensionales son:

{displaystyle T=t,M=m,L=ellg=ell /t^{2}.}

La matriz dimensional es:

{displaystyle mathbf {M} ={begin{bmatrix}1&0&0&-2\0&1&0&0\0&0&1&1end{bmatrix}}.}

(Las filas corresponden a las dimensiones ${displaystyle t,m,}$ y ${displaystyle ell}$ y las columnas a las variables dimensionales ${displaystyle T,M,L,{text{ and }}g.}$ Por ejemplo, la cuarta columna, ${displaystyle (-2,0,1),}$ declara que $g$ variable tiene dimensiones ${displaystyle t^{-2}m^{0}ell ^{1}.}$ )

Estamos buscando un vector de núcleo ${displaystyle a=left[a_{1},a_{2},a_{3},a_{4}right]}$ tal que el producto de la matriz $mathbf {M}$ on $a$ cede el vector cero ${displaystyle [0,0,0].}$ La matriz dimensional como se escribe arriba es en forma de echelon de fila reducida, por lo que se puede leer un vector de núcleo dentro de una constante multiplicativa:

{displaystyle a={begin{bmatrix}2\0\-1\1end{bmatrix}}.}

Si no estuviera ya reducido, se podría realizar la eliminación de Gauss-Jordan en la matriz dimensional para determinar más fácilmente el kernel. De ello se deduce que la constante adimensional se puede escribir:

{displaystyle {begin{aligned}pi &=T^{2}M^{0}L^{-1}g^{1}\&=gT^{2}/Lend{aligned}}.}

{displaystyle pi =(t)^{2}(m)^{0}(ell)^{-1}left(ell /t^{2}right)^{1}=1,}

En este ejemplo, tres de las cuatro cantidades dimensionales son unidades fundamentales, por lo que el último (que es $g$ ) debe ser una combinación de lo anterior.
Note que si $a_{2}$ (el coeficiente de $M$ ) no era cero entonces no habría manera de cancelar el $M$ valor; por consiguiente $a_{2}$ Debe ser cero. El análisis dimensional nos ha permitido concluir que el período del péndulo no es una función de su masa ${displaystyle M.}$ (En el espacio 3D de poderes de masa, tiempo y distancia, podemos decir que el vector de masa es linealmente independiente de los vectores para las otras tres variables. Hasta un factor de escalada, ${displaystyle {vec {g}}+2{vec {T}}-{vec {L}}}$ es la única manera notrivial de construir un vector de un parámetro sin dimensión.)

El modelo ahora se puede expresar como:

{displaystyle Fleft(gT^{2}/Lright)=0.}

Entonces esto implica que ${displaystyle gT^{2}/L=C_{i}}$ para algunos cero $C_{i}$ de la función $F.$ Si sólo hay un cero, llámalo ${displaystyle C,}$ entonces ${displaystyle gT^{2}/L=C.}$ Requiere más información física o un experimento para demostrar que en realidad sólo hay un cero y que la constante es dada por ${displaystyle C=4pi ^{2}.}$

Para grandes oscilaciones de un péndulo, el análisis se complica por un parámetro adimensional adicional, el ángulo máximo de oscilación. El análisis anterior es una buena aproximación a medida que el ángulo se aproxima a cero.

Otros ejemplos

Un ejemplo de análisis dimensional se puede encontrar para el caso de la mecánica de un disco giratorio delgado, sólido y de lados paralelos. Hay cinco variables involucradas que se reducen a dos grupos adimensionales. La relación entre estos se puede determinar mediante experimentos numéricos usando, por ejemplo, el método de elementos finitos.

El teorema también se ha utilizado en campos distintos de la física, por ejemplo, en las ciencias del deporte.

Contenido relacionado

Más resultados...