Puerta lógica cuántica
En la computación cuántica y específicamente en el modelo de computación del circuito cuántico, una puerta lógica cuántica (o simplemente una puerta cuántica) es un circuito cuántico básico que opera en un pequeño número de qubits. Las puertas lógicas cuánticas son los componentes básicos de los circuitos cuánticos, al igual que las puertas lógicas clásicas lo son para los circuitos digitales convencionales.
A diferencia de muchas puertas lógicas clásicas, las puertas lógicas cuánticas son reversibles. Es posible realizar computación clásica utilizando únicamente puertas reversibles. Por ejemplo, la puerta Toffoli reversible puede implementar todas las funciones booleanas, a menudo a costa de tener que utilizar bits auxiliares. La puerta de Toffoli tiene un equivalente cuántico directo, lo que demuestra que los circuitos cuánticos pueden realizar todas las operaciones realizadas por los circuitos clásicos.
Las puertas cuánticas son operadores unitarios, y se describen como matrices unitarias relativas a alguna base ortonormal. Por lo general base computacional se utiliza, que a menos que se comparó con algo, sólo significa que para un d- sistema cuántico de nivel (como un qubit, un registro cuántico, o qutritos y qudits) los vectores de base ortonormal son etiquetados Silencio0. . ,Silencio1. . ,... ... ,Silenciod− − 1. . {displaystyle tención0rangle sobrevivir1rangledots sometidad-1rangle }, o utilizar notación binaria.
Historia

La notación actual para las puertas cuánticas fue desarrollada por muchos de los fundadores de la ciencia de la información cuántica incluyendo Adriano Barenco, Charles Bennett, Richard Cleve, David P. DiVincenzo, Norman Margolus, Peter Shor, Tycho Sleator, John A. Smolin, y Harald Weinfurter, basándose en la notación presentada por Richard Feynman en 1986.
Representación

Rotaciones sobre x, y, z ejes de la esfera Bloch están representados por las puertas del operador de rotación.
Las puertas lógicas cuánticas están representadas por matrices unitarias. Una puerta que actúa n{displaystyle n} qubits es representado por un 2n× × 2n{displaystyle 2^{n}times 2^{n} matriz unitaria, y el conjunto de todas esas puertas con la operación del grupo de multiplicación de matriz es el grupo unitario U(2n). El cuántico declara que las puertas actúan sobre son vectores de unidad en 2n{displaystyle 2^{n} dimensiones complejas, con la compleja norma Euclideana (el 2-norm). Los vectores de base (a veces llamados eigenstates) son los resultados posibles si el estado de los qubits se mide, y un estado cuántico es una combinación lineal de estos resultados. Las puertas cuánticas más comunes operan en espacios vectoriales de uno o dos codos, al igual que las puertas lógicas clásicas comunes operan en uno o dos bits.
Aunque las puertas lógicas cuánticas pertenecen a grupos continuos de simetría, el hardware real es inexacto y por lo tanto limitado en precisión. La aplicación de las puertas normalmente introduce errores, y las fidelidades de los estados cuánticos disminuyen con el tiempo. Si se utiliza la corrección de error, las puertas utilizables se restringen aún más a un conjunto finito. Más adelante en este artículo, esto es ignorado ya que el foco está en las propiedades ideales de las puertas cuánticas.
Los estados cuánticos se representan típicamente por " Kets ", de una notación conocida como Bra -Ket.
La representación vectorial de un solo qubit es
- Silencioa. . =v0Silencio0. . +v1Silencio1. . → → [v0v1].{displaystyle Наrangle =v_{0} sobrevivir0rangle +v_{1} {begin{bmatrix}v_{0}v_{1}end{bmatrix}}
Aquí, v0{displaystyle V_{0} y v1{displaystyle v_{1} son las amplitudes de probabilidad complejas del qubit. Estos valores determinan la probabilidad de medir un 0 o un 1, al medir el estado del qubit. Vea la medición a continuación para más detalles.
El valor cero está representado por el ket Silencio0. . =[10]{displaystyle ¦0rangle ={begin{bmatrix}1end{bmatrix}}}, y el valor uno está representado por el ket Silencio1. . =[01]{fnMicrosoft}}.
El producto tensor (o producto Kronecker) se utiliza para combinar estados cuánticos. El estado combinado para un registro de qubit es el producto tensor de los qubits constituyentes. El producto tensor es denotado por el símbolo ⊗ ⊗ {displaystyle otimes }.
La representación vectorial de dos codos es:
- Silencio↑ ↑ . . =v00Silencio00. . +v01Silencio01. . +v10Silencio10. . +v11Silencio11. . → → [v00v01v10v11].{displaystyle TENpsi rangle ################################################################################################################################################################################################################################################################ {begin{bmatrix}v_{01}v_{10}v_{11}end{bmatrix}}}
La acción de la puerta en un estado cuántico específico se encuentra multiplicando el vector Silencio↑ ↑ 1. . {displaystyle ← _{1}rangle }, que representa el estado por la matriz U{displaystyle U} representando la puerta. El resultado es un nuevo estado cuántico Silencio↑ ↑ 2. . {displaystyle ← _{2}rangle }:
- USilencio↑ ↑ 1. . =Silencio↑ ↑ 2. . .{displaystyle U arrestpsi _{1}rangle = arrestpsi _{2}rangle.}
Ejemplos notables
Existe un número infinito e incontable de puertas. Algunos de ellos han sido nombrados por varios autores y a continuación se muestran algunos de los más utilizados en la literatura.
Puerta de identidad
La puerta de identidad es la matriz de identidad, generalmente escrita como I, y se define para un solo qubit como
- I=[1001],{displaystyle I={begin{bmatrix}1 {0}}
donde I es independiente de la base y no modifica el estado cuántico. La puerta de identidad es más útil cuando se describe matemáticamente el resultado de varias operaciones de puerta o cuando se analizan circuitos de múltiples qubits.
Puertas de Pauli (X,Y,Z)
Las puertas de Pauli ()X,Y,Z){displaystyle (X,Y,Z)} son las tres matrices Pauli ()σ σ x,σ σ Sí.,σ σ z){displaystyle (sigma _{x},sigma _{y},sigma _{z})} y actuar en un solo codo. El Pauli X, Y y Z equivalente, respectivamente, a una rotación alrededor de la x, Sí. y z ejes de la esfera Bloch por π π {displaystyle pi} radians.
Pauli...X puerta es el equivalente cuántico de la puerta NO para ordenadores clásicos con respecto a la base estándar Silencio0. . {displaystyle Silencioso, Silencio1. . {displaystyle ← }, que distingue z eje en la esfera Bloch. A veces se llama un poco de clip como mapas Silencio0. . {displaystyle Silencioso a Silencio1. . {displaystyle ← } y Silencio1. . {displaystyle ← } a Silencio0. . {displaystyle Silencioso. Del mismo modo, el Pauli-Y mapas Silencio0. . {displaystyle Silencioso a iSilencio1. . {displaystyle i tuberculosis1rangle } y Silencio1. . {displaystyle ← } a − − iSilencio0. . {displaystyle - Yo vivo.. Pauli Z deja el estado de base Silencio0. . {displaystyle Silencioso sin cambios y mapas Silencio1. . {displaystyle ← } a − − Silencio1. . {displaystyle - ¿Por qué?. Debido a esta naturaleza, Pauli Z a veces se llama Flip de fase.
Estas matrices generalmente se representan como
- X=σ σ x=NO=[0110],{displaystyle X=sigma ¿Por qué?
- Y=σ σ Sí.=[0− − ii0],{displaystyle Y=sigma ################################################################################################################################################################################################################################################################
- Z=σ σ z=[100− − 1].{displaystyle Z=sigma {fnMicrosoft Sans Serif}
Las matrices de Pauli son involutivas, lo que significa que el cuadrado de una matriz de Pauli es la matriz identidad.
- I2=X2=Y2=Z2=− − iXYZ=I{displaystyle I^{2}=X^{2}=Y^{2}=Z^{2}=-iXYZ=I}
Las matrices Pauli también anticomunicación, por ejemplo ZX=iY=− − XZ.{displaystyle ZX=iY=-XZ.}
La matriz exponencial de una matriz Pauli σ σ j{displaystyle sigma _{j} es un operador de rotación, a menudo escrito como e− − iσ σ jSilencio Silencio /2.{displaystyle e^{-isigma _{j}theta /2}
Puertas controladas

Las puertas controladas actúan en 2 o más codos, donde uno o más codos actúan como un control para alguna operación. Por ejemplo, la puerta controlada NO (o CNOT o CX) actúa en 2 codos, y realiza la operación NO en el segundo codo sólo cuando el primer codo es Silencio1. . {displaystyle ← }, y de otro modo lo deja sin cambios. Con respecto a la base Silencio00. . {displaystyle Silencioso, Silencio01. . {displaystyle ← }, Silencio10. . {displaystyle ← }, Silencio11. . {displaystyle ← }, está representado por la matriz unitaria Hermitiana:
- CNOT=[1000010000010010].{displaystyle {mbox{CNOT}}={begin{bmatrix}1 tendría0 unos cuantos0 cada uno menos.
El CNOT (o controlado Pauli-X) puerta se puede describir como la puerta que mapa la base estados Silencioa,b. . ↦ ↦ Silencioa,a⊕ ⊕ b. . {displaystyle tencióna,brangle mapsto tencióna,aoplus brangle }, donde ⊕ ⊕ {displaystyle oplus } es XOR.
El CNOT se puede expresar en la base de Pauli como:
- CNOT=eiπ π 4()I− − Z1)()I− − X2)=e− − iπ π 4()I− − Z1)()I− − X2).{displaystyle {mbox{CNOT}=e^{i{frac {pi} [I-Z_{1}) (I-X_{2}=e^{-i{frac {pi) (I-Z_{1}) (I-X_{2}).}
Siendo un operador unitario Hermitiano, CNOT tiene la propiedad que eiSilencio Silencio U=()# Silencio Silencio )I+()ipecado Silencio Silencio )U{displaystyle e^{itheta U}=(cos theta)I+(isin theta)U} y U=eiπ π 2()I− − U)=e− − iπ π 2()I− − U){displaystyle U=e^{i{frac {fnMicroc} ¿Qué?, y es involutivo.
De manera más general, si U es una puerta que opera en un solo qubit con representación matricial
- U=[u00u01u10u11],{displaystyle ¿Qué?
entonces la puerta U controlada es una puerta que opera en dos qubits de tal manera que el primer qubit sirve como control. Mapea los estados básicos de la siguiente manera.
- Silencio00. . ↦ ↦ Silencio00. . {displaystyle tención00rangle mapsto Silencio00rangle
- Silencio01. . ↦ ↦ Silencio01. . {displaystyle tención01rangle mapsto tención01rangle }
- Silencio10. . ↦ ↦ Silencio1. . ⊗ ⊗ USilencio0. . =Silencio1. . ⊗ ⊗ ()u00Silencio0. . +u10Silencio1. . ){displaystyle TENED 10rangle mapsto tención1rangle otimes U WordPress0rangle = duración1rangle otimes (u_{00} duración0rangle +u_{10} persistencia1rangle)}
- Silencio11. . ↦ ↦ Silencio1. . ⊗ ⊗ USilencio1. . =Silencio1. . ⊗ ⊗ ()u01Silencio0. . +u11Silencio1. . ){displaystyle tención11rangle mapsto tención1rangle otimes U WordPress1rangle = duración1rangle otimes (u_{01} duración0rangle +u_{11} persistencia1rangle)}
la matriz que representa el u controlado es
- CU=[1000010000u00u0100u10u11].{displaystyle {mbox{C}U={begin{bmatrix}1 tendría0 igual0 rest1 tendría0}}}}} {}} {0}}} {} {}}} {mbox{bmatrix}}}}
Cuando U es uno de los operadores de Pauli, X,Y, Z, los términos respectivos & #34;controlado-X", "controlado-Y" o "controlado-Z" a veces se utilizan. A veces esto se reduce a solo CX, CY y CZ.
En general, cualquier puerta unitaria qubit puede expresarse como U=eiH{displaystyle U=e^{iH}, donde H es una matriz hermitiana, y luego el control U es CU=ei12()I− − Z1)H2.{displaystyle CU=e^{i{frac {1} {2} {I-Z_{1})H_{2}}
El control se puede extender a puertas con un número arbitrario de qubits y funciones en lenguajes de programación. Las funciones pueden estar condicionadas a estados de superposición.
Control clásico

En los diagramas de circuito, las líneas individuales son codos, y las líneas duplicadas son bits.
Las puertas también pueden controlarse mediante la lógica clásica. Una computadora cuántica está controlada por una computadora clásica y se comporta como un coprocesador que recibe instrucciones de la computadora clásica sobre qué puertas ejecutar en qué qubits. El control clásico es simplemente la inclusión u omisión de puertas en la secuencia de instrucciones de la computadora cuántica.
Puertas de cambio de fase
El cambio de fase es una familia de puertas de un solo codo que mapean los estados de base Silencio0. . ↦ ↦ Silencio0. . {displaystyle TENSITO0rangle mapsto Silencio. y Silencio1. . ↦ ↦ eiφ φ Silencio1. . {displaystyle tención1rangle mapsto e^{ivarphi . . .. La probabilidad de medir un Silencio0. . {displaystyle Silencioso o Silencio1. . {displaystyle ← } no cambia después de aplicar esta puerta, sin embargo modifica la fase del estado cuántico. Esto equivale a trazar un círculo horizontal (una línea de latitud constante), o una rotación sobre el eje z en la esfera Bloch por φ φ {displaystyle varphi } radians. La puerta de cambio de fase está representada por la matriz:
- P()φ φ )=[100eiφ φ ]{displaystyle P(varphi)={begin{bmatrix}1 {0}}}}
Donde φ φ {displaystyle varphi } es Cambio de fase con el período 2π. Algunos ejemplos comunes son los T puerta donde φ φ =π π 4{textstyle varphi ={frac {pi} } {4}} (históricamente conocido como π π /8{displaystyle pi /8} puerta), la puerta de fase (también conocida como la puerta S, escrita como S, aunque S a veces se utiliza para las puertas SWAP) donde φ φ =π π 2{textstyle varphi ={frac {pi} } {2}} y la puerta de Pauli-Z donde φ φ =π π {displaystyle varphi =pi}.
Las puertas del cambio de fase se relacionan entre sí de la siguiente manera:
- Z=[100eiπ π ]=[100− − 1]=P()π π ){displaystyle Z={begin{bmatrix}1 tendría0}}end{bmatrix}={begin{bmatrix}1⁄0}=Pleft(piright)}}
- S=[100eiπ π 2]=[100i]=P()π π 2)=Z{displaystyle S={begin{bmatrix}1 tendría0 {begin{bmatrix}={begin{bmatrix}1 limit0 limitiend{bmatrix}}=Pleft({frac {pi }{2}right)={sqrt {Z}}}}}}}} {f}}}} {f}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}f}}}}}}}}}}}}}}}}}}} {f} {f} {f}}}}}}}f}}}}}}}}}}}}}}}f}}}}}}}}}}}}}}}}}}}}}f}f}f}f}f}f}}f}f}f}}f}f}f}}f}}f}f}f}f}}
- T=[100eiπ π 4]=P()π π 4)=S=Z4{displaystyle T={begin{bmatrix}1 tendría0}} } {4}}end{bmatrix}=Pleft({frac {pi) - Sí. {S}={sqrt [{4} {Z}} {}}} {}}} {}}} {}}} {}}}} {}}}}}} {}}}}}} {}}}} {}}}}}} {}}}} {}}}}}} {}}}}}}}} {}}} {}}}}} {}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}} {}}}}}}} {}}}}}} {}}}} {}}}}}}}}}}}}} {}}}}}}}}}}} {}}}}} {}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}
Note que la puerta de la fase P()φ φ ){displaystyle P(varphi)} no es Hermitian (excepto para todos φ φ =nπ π ,n▪ ▪ Z{displaystyle varphi =npinin mathbb {Z}). Estas puertas son diferentes de sus conjugados Hermitianos: P† † ()φ φ )=P()− − φ φ ){displaystyle P^{dagger }(varphi)=P(-varphi)}. Las dos puertas adyacentes (o conjugadas) S† † {displaystyle - Sí. y T† † {displaystyle T^{dagger } a veces se incluyen en conjuntos de instrucciones.
Puerta de Hadamard
La puerta de Hadamard o Walsh-Hadamard, llamada por Jacques HadamardFrancés: [adama]) y Joseph L. Walsh, actúa en un solo cuarto. mapea los estados de base Silencio0. . ↦ ↦ Silencio0. . +Silencio1. . 2{textstyle Silencio0rangle mapsto {fnMicroc {rangle + preserven]} {sqrt {2}}} y Silencio1. . ↦ ↦ Silencio0. . − − Silencio1. . 2{textstyle Silencio1rangle mapsto {fnMicroc - ¿Qué? (crea un estado de superposición igual si se da un estado de base computacional). Los dos estados ()Silencio0. . +Silencio1. . )/2{displaystyle (vivir0rangle + sobrevivir1rangle)/{sqrt {2}} y ()Silencio0. . − − Silencio1. . )/2{displaystyle (vivir0rangle - perpetua1rangle)/{sqrt {2}} a veces escrito Silencio+. . {displaystyle ← } y Silencio− − . . {displaystyle ← } respectivamente. La puerta de Hadamard realiza una rotación de π π {displaystyle pi} sobre el eje ()x^ ^ +z^ ^ )/2{displaystyle ({hat {x}+{hat {z})/{sqrt {2}}} en la esfera Bloch, y por lo tanto es involutivo. Está representado por la matriz Hadamard:
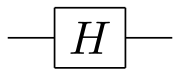
- H=12[111− − 1].{displaystyle H={frac {1}{sqrt {2}{begin{bmatrix}1 limit11 {1}}}}
Si el Hermitian (también H† † =H− − 1=H{displaystyle H^{dagger }=H^{-1}=H}) La puerta de Hadamard se utiliza para realizar un cambio de base, voltea x^ ^ {displaystyle {hat {x}} y z^ ^ {displaystyle {hat {z}}}. Por ejemplo, HZH=X{displaystyle HZH=X} y HXH=Z=S.{displaystyle H{sqrt {X};H={sqrt {Z}=S.}
Puerta de intercambio

La puerta de intercambio cambia dos codos. Con respecto a la base Silencio00. . {displaystyle Silencioso, Silencio01. . {displaystyle ← }, Silencio10. . {displaystyle ← }, Silencio11. . {displaystyle ← }, está representado por la matriz
- SWAP=[1000001001000001].{displaystyle {mbox{SWAP}}={begin{bmatrix}1 tendría0 unos cuantos0 unos cuantos,0 unos cuantos menos.
La puerta del swap se puede descomponer en forma de summation:
- SWAP=I⊗ ⊗ I+X⊗ ⊗ X+Y⊗ ⊗ Y+Z⊗ ⊗ Z2{displaystyle {mbox{SWAP}={frac} {Iotimes I+Xotimes X+Yotimes Y+Zotimes Z}{2}
Puerta de Toffoli (CCNOT)
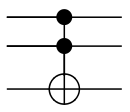
La puerta Toffoli, llamada por Tommaso Toffoli y también llamada la puerta CCNOT o la puerta Deutsch D()π π /2){displaystyle D(pi /2)}, es una puerta de 3 bits que es universal para la computación clásica pero no para la computación cuántica. La puerta de Toffoli cuántica es la misma puerta, definida por 3 codos. Si nos limitamos a aceptar sólo cubitos de entrada que son Silencio0. . {displaystyle Silencioso y Silencio1. . {displaystyle ← }, entonces si los dos primeros pedazos están en el estado Silencio1. . {displaystyle ← } se aplica a Pauli-X (o NO) en la tercera parte, de lo contrario no hace nada. Es un ejemplo de una puerta unitaria controlada por CC-U. Puesto que es el análogo cuántico de una puerta clásica, está completamente especificado por su tabla de la verdad. La puerta de Toffoli es universal cuando se combina con la puerta de Hadamard de qubit único.
| Tabla de la verdad | Forma de matriz | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [1000000001000000001000000001000000001000000001000000000100000010]{}0 {}0}0}0}0}0}0}0}0}0 {0}0}0 {0}0}0}0 {0}0}0 {0}0}0}0 {0}0}0}0 {0}0}0}0 {}0} | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
La puerta de Toffoli está relacionada con el clásico Y (∧ ∧ {displaystyle land }Y XOR⊕ ⊕ {displaystyle oplus }) operaciones como realiza el mapeo Silencioa,b,c. . ↦ ↦ Silencioa,b,c⊕ ⊕ ()a∧ ∧ b). . {displaystyle На,b,crangle mapsto Silencio, b,coplus (aland b)rangle } sobre estados en base computacional.
La puerta de Toffoli se puede expresar usando matrices de Pauli como
- Toff=eiπ π 8()I− − Z1)()I− − Z2)()I− − X3)=e− − iπ π 8()I− − Z1)()I− − Z2)()I− − X3).{displaystyle {mbox{}=e^{i{frac {pi} ¿Qué? (I-Z_{1}) (I-Z_{2})}
Puertas cuadradas universales

Un conjunto de puertas cuánticas universales es cualquier conjunto de puertas al que se puede reducir cualquier operación posible en una computadora cuántica, es decir, cualquier otra operación unitaria se puede expresar como una secuencia finita de puertas. del conjunto. Técnicamente, esto es imposible con algo menos que un conjunto incontable de puertas, ya que el número de puertas cuánticas posibles es incontable, mientras que el número de secuencias finitas de un conjunto finito es contable. Para resolver este problema, sólo requerimos que cualquier operación cuántica pueda aproximarse mediante una secuencia de puertas de este conjunto finito. Además, para unidades unitarias con un número constante de qubits, el teorema de Solovay-Kitaev garantiza que esto se puede hacer de manera eficiente. Se puede comprobar si un conjunto de puertas cuánticas es universal utilizando métodos de teoría de grupos y/o en relación con diseños t unitarios (aproximados).
Algunos conjuntos de puertas cuánticas universales incluyen:
- Los operadores de rotación Rx()Silencio), RSí.()Silencio), Rz()Silencio), la puerta del cambio de fase P()φ) y CNOT se utilizan comúnmente para formar un conjunto de puertas cuánticas universales.
- El Clifford set {CNOT, H, S} + T Puerta. El conjunto Clifford no es un conjunto universal de puertas cuánticas, ya que se puede simular de manera eficiente clásica según el teorema Gottesman–Knill.
- La puerta Toffoli + Puerta Hadamard. La puerta de Toffoli por sí sola forma un conjunto de puertas universales para circuitos algebraicos booleanos reversibles, que abarca toda la computación clásica.
Puerta alemana
Un conjunto de puertas cuadradas universales también se puede formular utilizando la parametrizada puerta Deutsch de tres codos D()Silencio Silencio ){displaystyle D(theta)}, llamado por el físico David Deutsch. Es un caso general CC-Uo unitario controlado por control controlado puerta, y se define como
- Silencioa,b,c. . ↦ ↦ {}i# ()Silencio Silencio )Silencioa,b,c. . +pecado ()Silencio Silencio )Silencioa,b,1− − c. . para a=b=1,Silencioa,b,c. . de otra manera.{begin{cases}icos(theta) habita,b,crangle +sin(theta) perpetuaa,b,crangle +sin(theta) perpetuaa,b,1-crangle >{text{for}} a=b=1,flasha,b,crend {text {otherwise}}}}}}}}}} {f}}}}}} {displaystyle.
Desafortunadamente, una puerta Deutsch en funcionamiento permanece fuera de nuestro alcance debido a la falta de un protocolo. Hay algunas propuestas para realizar una puerta Deutsch con interacción dipolo-dipolo en átomos neutros.
Una puerta lógica universal para la computación clásica reversible, la puerta Toffoli, es reducible a la puerta Deutsch D()π π /2){displaystyle D(pi /2)}, mostrando así que todas las operaciones de lógica clásica reversibles se pueden realizar en un ordenador cuántico universal.
También existen puertas únicas de dos qubits suficientes para la universalidad. En 1996, Adriano Barenco demostró que la puerta Deutsch se puede descomponer utilizando una única puerta de dos qubits (puerta Barenco), pero es difícil realizarlo experimentalmente. Esta característica es exclusiva de los circuitos cuánticos, ya que no existe una puerta clásica de dos bits que sea a la vez reversible y universal. Se podrían implementar puertas universales de dos qubits para mejorar los circuitos reversibles clásicos en microprocesadores rápidos de baja potencia.
Composición del circuito
Puertas cableadas en serie

Supongamos que tenemos dos puertas A y B que ambos actúan n{displaystyle n} Cubitos. Cuando B es puesto después A en un circuito de serie, entonces el efecto de las dos puertas se puede describir como una sola puerta C.
- C=B⋅ ⋅ A{displaystyle C=Bcdot A}
Donde ⋅ ⋅ {displaystyle cdot } es multiplicación de matriz. La puerta resultante C tendrá las mismas dimensiones A y B. El orden en que las puertas aparecen en un diagrama de circuito se invierte cuando se multiplican juntas.
Por ejemplo, colocar la puerta Pauli X después de la puerta Pauli Y, las cuales actúan en un solo qubit, puede describirse como una única puerta combinada C:
- C=X⋅ ⋅ Y=[0110]⋅ ⋅ [0− − ii0]=[i00− − i]=iZ{displaystyle C=Xcdot Y={begin{bmatrix}0 tarde111}bmatrix}cdot {begin{bmatrix}0 {ii}i}={bmatrix}}={begin{bmatrix}i}0 âTMiend{bmatrix}=iZ}
El símbolo del producto (⋅ ⋅ {displaystyle cdot }) es a menudo omitido.
Exponentes de puertas cuánticas
Todos los exponentes reales de matrices unitarias también son matrices unitarias, y todas las puertas cuánticas son matrices unitarias.
Los exponentes de números enteros positivos son equivalentes a secuencias de puertas cableadas en serie (por ejemplo. X3=X⋅ ⋅ X⋅ ⋅ X{displaystyle Xcdot Xcdot X}), y los verdaderos exponentes es una generalización del circuito de serie. Por ejemplo, Xπ π {displaystyle X^{pi}} y X=X1/2{displaystyle {sqrt {X}=X^{1/2} son ambas puertas cuánticas válidas.
U0=I{displaystyle U^{0}=I} para cualquier matriz unitaria U{displaystyle U}. La matriz de identidad (I{displaystyle I}) se comporta como un NOP y puede ser representado como alambre desnudo en circuitos cuánticos, o no se muestra en absoluto.
Todas las puertas son matrices unitarias, para que U† † U=UU† † =I{displaystyle U^{dagger }U=UU^{dagger }=I} y U† † =U− − 1{displaystyle U^{dagger }=U^{-1}, Donde † † {displaystyle dagger } es la transposición conyugal. Esto significa que los exponentes negativos de las puertas son inversos unitarios de sus contrapartes positivamente exponentes: U− − n=()Un)† † {displaystyle ¿Qué?. Por ejemplo, algunos exponentes negativos de las puertas de cambio de fase son T− − 1=T† † {displaystyle T^{-1}=T^{dagger} y T− − 2=()T2)† † =S† † {displaystyle T^{-2}=(T^{2})^{dagger }=S^{dagger }.
Note que para una matriz hermitiana H† † =H,{displaystyle H^{dagger }=H,} y debido a la unidad, HH† † =I,{displaystyle HH^{dagger Yo... Así que... H2=I{displaystyle H^{2}=I} por todas las puertas de Hermitian. Son involutivos. Ejemplos de puertas de Hermitian son las puertas de Pauli, Hadamard, CNOT, SWAP y Toffoli. Cada matriz unitaria Hermitiana H{displaystyle H. tiene la propiedad que eiSilencio Silencio H=()# Silencio Silencio )I+()ipecado Silencio Silencio )H{displaystyle e^{itheta H}=(cos theta)I+(isin theta)H} Donde H=eiπ π 2()I− − H)=e− − iπ π 2()I− − H).{displaystyle H=e^{i{frac {pi - ¿Qué?
Puertas paralelas

El producto tensor (o producto de Kronecker) de dos puertas cuánticas es la puerta que es igual a las dos puertas en paralelo.
Si, como en la imagen, combinamos la puerta Pauli-Y con la puerta Pauli-X en paralelo, entonces esto se puede escribir como:
- C=Y⊗ ⊗ X=[0− − ii0]⊗ ⊗ [0110]=[0[0110]− − i[0110]i[0110]0[0110]]=[000− − i00− − i00i00i000]{displaystyle C=Yotimes ################################################################################################################################################################################################################################################################
Ambos Pauli...X y el Pauli...Y acto de puerta en un solo cuarto. La puerta resultante C{displaystyle C} actuar en dos codos.
A veces se omite el símbolo del producto tensor, y los índices se utilizan para los operadores en su lugar.
Transformación de Hadamard
La puerta H2=H⊗ ⊗ H{displaystyle H_{2}=Hotimes H. es la puerta de Hadamard ()H{displaystyle H.) aplicado en paralelo en 2 codos. Puede ser escrito como:
- H2=H⊗ ⊗ H=12[111− − 1]⊗ ⊗ 12[111− − 1]=12[11111− − 11− − 111− − 1− − 11− − 1− − 11]{displaystyle H_{2}=Hotimes H={frac {1}{sqrt {2}{begin{bmatrix}1 limit111end{bmatrix}otimes {frac {1}{sqrt {2}}}{begin{bmatrix}1}1trix} {1111111mmmmmmccccccccccccccccccccccc} {cccccccccc} {cccccccccccccc} {cc} {cc} {ccccHcccccccc} {1}{2}{begin{bmatrix}1 tendrían un efecto11}}}}}}}}
Esta "puerta de Hadamard paralela de dos codos" será, cuando se aplique, por ejemplo, al vencedor cero de dos codos ()Silencio00. . {displaystyle Silencioso), crear un estado cuántico que tenga igual probabilidad de ser observado en cualquiera de sus cuatro posibles resultados; Silencio00. . {displaystyle Silencioso, Silencio01. . {displaystyle ← }, Silencio10. . {displaystyle ← }, y Silencio11. . {displaystyle ← }. Podemos escribir esta operación como:
- H2Silencio00. . =12[11111− − 11− − 111− − 1− − 11− − 1− − 11][1000]=12[1111]=12Silencio00. . +12Silencio01. . +12Silencio10. . +12Silencio11. . =Silencio00. . +Silencio01. . +Silencio10. . +Silencio11. . 2{displaystyle ¿Qué? {1}{2}{begin{bmatrix}1 tendrían un efecto11}1}1} {1}}}begin{bmatrix}1end{bmatrix}={fractrix}={frac}}={frac}{}{}}}}}}}{b}}}}}}}}}}{begin{begin{b}}}}}}}}}}}}}}}}}}}bbegin{begin{begin{begin{begin{bn}}bbn}}bn}bn}bbn}bn}}}}bbb {1}{2}{begin{bmatrix}1111end{bmatrix}}={frac {1}{2} {1}{2} {1}{2} {1}{2} ################################################################################################################################################################################################################################################################
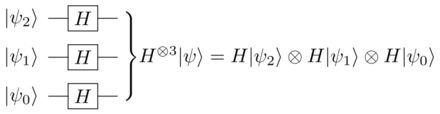
Aquí está la amplitud de cada estado mensurable 1.2. La probabilidad de observar cualquier estado es el cuadrado del valor absoluto de la amplitud de los estados mensurables, que en el ejemplo anterior significa que hay uno en cuatro que observamos cualquiera de los cuatro casos individuales. Vea la medición para detalles.
H2{displaystyle H_{2} realiza la transformación Hadamard en dos codos. Del mismo modo la puerta H⊗ ⊗ H⊗ ⊗ ⋯ ⋯ ⊗ ⊗ H⏟ ⏟ n veces=⨂ ⨂ 1nH=H⊗ ⊗ n=Hn{displaystyle underbrace {Hotimes Hotimes dots otimes H} {n{text{ times}=bigotimes ¿Por qué? No. realiza una transformación Hadamard en un registro de n{displaystyle n} Cubitos.
Cuando se aplica a un registro n{displaystyle n} qubits all initialized to Silencio0. . {displaystyle Silencioso, la transformación Hadamard pone el registro cuántico en una superposición con igual probabilidad de ser medido en cualquiera de sus 2n{displaystyle 2^{n} estados posibles:
- ⨂ ⨂ 0n− − 1()HSilencio0. . )=12n[11⋮ ⋮ 1]=12n()Silencio0. . +Silencio1. . +⋯ ⋯ +Silencio2n− − 1. . )=12n. . i=02n− − 1Silencioi. . {displaystyle bigotimes {0} {fn} {fnMicrosoft Sans Serif} {fn}} {begin{bmatrix}11\\vdots11end{bmatrix}={fracfnMicroc}= {fnMicroc} {1}{sqrt {2} {fn} {fn}} {fn}} {fn}} {\fn}} {fn}}}} {fn}}} {fn}} {fn}}}}}} {f}}}}}} { Grande (} sobrevivir0rangle + sobrevivir1rangle + 'dots + sobrevivir2^{n}-1rangle {Big}={frac {1} {sqrt {2}}}sum}} {fn}} {fn}} {fn}}} {fn}}}} {fn}} {fn}} {fn}} {fnK}}}}} {fnKfn}}}} {f}}}}}}}}}}}} {f}}}}}}}}}}}} {f}}}}}}}}}}}}}}}} {f}}}} {f}}}}}}}}}} {f}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}} ¿Por qué?
Este estado es una superposición uniforme y se genera como primer paso en algunos algoritmos de búsqueda, por ejemplo en amplificación de amplitud y estimación de fase.
Medir este estado resulta en un número aleatorio entre Silencio0. . {displaystyle Silencioso y Silencio2n− − 1. . {displaystyle Ø2n}. Cuán aleatorio es el número depende de la fidelidad de las puertas lógicas. Si no se mide, es un estado cuántico con igual amplitud de probabilidad 12n{displaystyle {frac {fn}} {fn}}} {fn}} {fn}} {fn}} {fn}}} {fn}}}}} {fn}}}}}}}}}}} {fn}}}}} {fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { para cada uno de sus posibles estados.
El Hadamard transforma los actos en un registro Silencio↑ ↑ . . {displaystyle Нpsi rangle } con n{displaystyle n} qubits such that Silencio↑ ↑ . . =⨂ ⨂ i=0n− − 1Silencio↑ ↑ i. . {textstyle tenciónpsi rangle =bigotimes _{i=0} {n-1} - ¿Qué? como sigue:
- ⨂ ⨂ 0n− − 1HSilencio↑ ↑ . . =⨂ ⨂ i=0n− − 1Silencio0. . +()− − 1)↑ ↑ iSilencio1. . 2=12n⨂ ⨂ i=0n− − 1()Silencio0. . +()− − 1)↑ ↑ iSilencio1. . )=HSilencio↑ ↑ 0. . ⊗ ⊗ HSilencio↑ ↑ 1. . ⊗ ⊗ ⋯ ⋯ ⊗ ⊗ HSilencio↑ ↑ n− − 1. . {displaystyle bigotimes ¿Qué? ################################################################################################################################################################################################################################################################ {fnK}} {fnK}}bigotimes ¿Qué? Grande (} habit0rangle +(-1)^{psi _{i} resist1rangle {Big)}=H foreverpsi _{0}rangle otimes H imperpsi _{1}rangle otimes cdots otimes H durablepsi - ¿Qué?
Aplicación sobre estados entrelazados
Si dos o más qubits se consideran un único estado cuántico, este estado combinado es igual al producto tensorial de los qubits constituyentes. Cualquier estado que pueda escribirse como un producto tensor de los subsistemas constituyentes se denomina estados separables. Por otro lado, un estado entrelazado es cualquier estado que no puede ser factorizado mediante tensor, o en otras palabras: Un estado entrelazado no puede escribirse como un producto tensorial de sus estados de qubits constituyentes. Se debe tener especial cuidado al aplicar puertas a qubits constituyentes que forman estados entrelazados.
Si tenemos un conjunto de N qubits que están enredados y desean aplicar una puerta cuántica en M c) N cuartos en el set, tendremos que extender la puerta para tomar N Qubits. Esta aplicación se puede hacer combinando la puerta con una matriz de identidad tal que su producto tensor se convierte en una puerta que actúa en N Cubitos. La matriz de identidad ()I{displaystyle I}) es una representación de la puerta que mapea cada estado a sí mismo (es decir, no hace nada en absoluto). En un diagrama de circuito la puerta de identidad o matriz aparecerá a menudo como un alambre desnudo.

Por ejemplo, la puerta de Hadamard ()H{displaystyle H.) actúa en un solo codo, pero si lo alimentamos el primero de los dos codos que constituyen el enredado Estado de Bell Silencio00. . +Silencio11. . 2{\displaystyle {frac {fnh00rangle} {f}}}}}} {fn}}}}}}}, no podemos escribir esa operación fácilmente. Necesitamos extender la puerta de Hadamard H{displaystyle H. con la puerta de identidad I{displaystyle I} para que podamos actuar en estados cuánticos dos. qubits:
- K=H⊗ ⊗ I=12[111− − 1]⊗ ⊗ [1001]=12[1010010110− − 10010− − 1]{displaystyle K=Hotimes I={frac {1}{sqrt {2}{begin{bmatrix}1 limit1111end{bmatrix}otimes {begin{bmatrix}1}{begin{bmatrix}={frac {1}{sqrt {2}}}}{begin{bmatrix}1 tendrían una relación0}}} {}}}} {begin{bmatrix}}}}} {begin{bmatrix}}}}} {begin{begin{bmatrix}}}}}}}}}}}}}}}}}} {begin{begin{begin{bmatrix}{bmatrix}}}}}}}}}}}}}}}}}}}}{begin{begin{bmatrix}}={bmatrix}}}}}}}={begin{bmatrix}}}}}}={bmatrix}}}}}}}}}}}}}}}}}}}}}}}}}}}}
La puerta K{displaystyle K} ahora se puede aplicar a cualquier estado de dos codos, enredado o de otro modo. La puerta K{displaystyle K} dejará el segundo cuarto sin tocar y aplicará la transformación Hadamard al primer codo. Si se aplica al estado de Bell en nuestro ejemplo, podemos escribir que:
- KSilencio00. . +Silencio11. . 2=12[1010010110− − 10010− − 1]12[1001]=12[111− − 1]=Silencio00. . +Silencio01. . +Silencio10. . − − Silencio11. . 2{displaystyle K{frac {0rangle + Anterior11rangle }{sqrt {2}}={frac {1}{sqrt {2}}{begin{bmatrix}1 limit0 {0}}} {}}{sqrt {2}}}}}{begin{bmatrix} {2}}} {begin{begin{bmatrix}} {2}}}}} {}}}}}}} {={f}}}}}}} {m}}}}}} {m} {sqm}}} {sqsqsqsqsqsq} {sq} {sqsq} {sq} {sq} {sq} {sq} {sq}} {sqsqsqsq} {sq} {sq} {sq} {sq} {sq} {sq} {sq}}}} {sq {1} {1end{bmatrix}}={frac {1}{2}{begin{bmatrix}11111end{bmatrix}={frac ################################################################################################################################################################################################################################################################
Computacional complejidad y el producto tensor
La complejidad del tiempo para multiplicar dos n× × n{displaystyle ntimes n}- Las matemáticas son al menos Ω Ω ()n2log n){displaystyle Omega (n^{2}log n)}, si usa una máquina clásica. Porque el tamaño de una puerta que funciona q{displaystyle q} qubits is 2q× × 2q{displaystyle 2^{q}times 2^{q} significa que el tiempo para simular un paso en un circuito cuántico (por medio de multiplicar las puertas) que opera en estados enredados genéricos es Ω Ω ()2q2log ()2q)){displaystyle Omega ({2^{q}} {2}log ({2^{q})})}. Por esta razón se cree que es intráctil simular grandes sistemas cuánticos enredados usando computadoras clásicas. Subsets of the gates, such as the Clifford gates, or the trivial case of circuits that only implement classic Boolean functions (e.g. combinations of X, CNOT, Toffoli), can however be efficient simulated on classic computers.
El vector estatal de un registro cuántico con n{displaystyle n} qubits is 2n{displaystyle 2^{n} entradas complejas. Robar las amplitudes de probabilidad como una lista de valores de puntos flotantes no es traccionable para grandes n{displaystyle n}.
Inversión unitaria de puertas

Debido a que todas las puertas lógicas cuánticas son reversibles, cualquier composición de múltiples puertas también es reversible. Todos los productos y productos tensoriales (es decir, combinaciones en serie y en paralelo) de matrices unitarias también son matrices unitarias. Esto significa que es posible construir una inversa de todos los algoritmos y funciones, siempre que contengan sólo puertas.
La inicialización, la medición, la E/S y la decoherencia espontánea son efectos secundarios en las computadoras cuánticas. Sin embargo, las puertas son puramente funcionales y biyectivas.
Si U{displaystyle U} es una matriz unitaria, entonces U† † U=UU† † =I{displaystyle U^{dagger }U=UU^{dagger }=I} y U† † =U− − 1{displaystyle U^{dagger }=U^{-1}. La daga† † {displaystyle dagger }) denota la transposición conyugal. También se llama adjoint de Hermitian.
Si una función F{displaystyle F} es un producto de m{displaystyle m} puertas, F=A1⋅ ⋅ A2⋅ ⋅ ⋯ ⋯ ⋅ ⋅ Am{displaystyle F=A_{1}cdot A_{2}cdot dots cdot A_{m}}, el inverso unitario de la función F† † {displaystyle F^{dagger} se puede construir:
Porque... ()UV)† † =V† † U† † {displaystyle (UV)^{dagger }=V^{dagger }U^{dagger } tenemos, después de la aplicación repetida en sí mismo
- F† † =()∏ ∏ i=1mAi)† † =∏ ∏ i=m1Ai† † =Am† † ⋅ ⋅ ⋯ ⋯ ⋅ ⋅ A2† † ⋅ ⋅ A1† † {displaystyle F^{dagger }=left(prod ¿Por qué? ¿Qué? }=A_{m}{dagger }cdot dots cdot ¿Qué?
Del mismo modo si la función G{displaystyle G. consta de dos puertas A{displaystyle A} y B{displaystyle B} en paralelo, entonces G=A⊗ ⊗ B{displaystyle G=Aotimes B. y G† † =()A⊗ ⊗ B)† † =A† † ⊗ ⊗ B† † {displaystyle G^{dagger }=(Aotimes B)^{dagger }=A^{dagger }otimes B^{dagger }.
Las puertas que son sus propios inversos unitarios se llaman Hermitian o autoadjuntos operadores. Algunas puertas elementales como el Hadamard (H) y las puertas de Pauli (I, X, Y, Z) son operadores ermitianos, mientras que otros como el cambio de fase (S, T, PPor lo general las puertas no son.
Por ejemplo, un algoritmo de suma se puede utilizar para la resta, si se "ejecuta al revés", como su inverso unitario. La transformada cuántica inversa de Fourier es la inversa unitaria. Las inversas unitarias también se pueden utilizar para no realizar cálculos. Los lenguajes de programación para computadoras cuánticas, como Q# de Microsoft, QCL de Bernhard Ömer y Qiskit de IBM, contienen inversión de funciones como conceptos de programación.
Medición
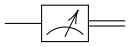
La medición (a veces llamada observación) es irreversible y, por lo tanto, no es una puerta cuántica, porque asigna el estado cuántico observado a un único valor. La medición toma un estado cuántico y lo proyecta a uno de los vectores base, con una probabilidad igual al cuadrado de la longitud del vector (en la norma 2) a lo largo de ese vector base. Esto se conoce como regla de Born y aparece como una operación estocástica no reversible, ya que establece probabilísticamente el estado cuántico igual al vector base que representa el estado medido. En el momento de la medición, se dice que el Estado “colapsa”; al valor único definido que se midió. Por qué y cómo, o incluso si el estado cuántico colapsa durante la medición, se denomina problema de medición.
La probabilidad de medir un valor con amplitud de probabilidad φ φ {displaystyle phi } es 1≥ ≥ Silencioφ φ Silencio2≥ ≥ 0{displaystyle 1geq Silenciophi TENSI}geq 0}, Donde Silencio⋅ ⋅ Silencio{displaystyle Silencioso es el módulo.
Medir un solo qubit, cuyo estado cuántico está representado por el vector aSilencio0. . +bSilencio1. . =[ab]{begin{bmatrix}abend{bmatrix}}}, se traducirá en Silencio0. . {displaystyle Silencioso con probabilidad SilencioaSilencio2{displaystyle Silencioso, y dentro Silencio1. . {displaystyle ← } con probabilidad SilenciobSilencio2{displaystyle Silencioso.
Por ejemplo, medir un codo con el estado cuántico Silencio0. . − − iSilencio1. . 2=12[1− − i]{displaystyle {frac {ы0rangle -iSobrevivir1rangle {fn} {fn} {fn} {fn} {fn} {begin{bmatrix}1-iend{bmatrix}}}}} {fn}}} {fn}}} {fn}}}} {fnf}}}}} {fnf}}}}}}}}} {f}}}}}}}}}}}}}}} {f} {f}}} {f}}}} {f}}}}}}} {f} {f}}}}}}} {f}}}}}}}}}}}}}}}}}}} {f}}}} {f}}}}} {f}}}} {f}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}} cederá con igual probabilidad Silencio0. . {displaystyle Silencioso o Silencio1. . {displaystyle ← }.
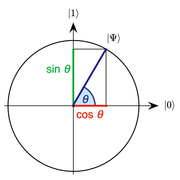
Nota: SilencioaSilencio2{displaystyle Silencioso es la probabilidad de medición Silencio0. . {displaystyle Silencioso y SilenciobSilencio2{displaystyle Silencioso es la probabilidad de medición Silencio1. . {displaystyle ← }.
Un estado cuántico SilencioΨ Ψ . . {displaystyle Silencioso rangle } que abarca n qubits se puede escribir como vector en 2n{displaystyle 2^{n} dimensiones complejas: SilencioΨ Ψ . . ▪ ▪ C2n{displaystyle SilencioPsi rangle in mathbb {C} ^{2^{n}}. Esto es porque el producto del tensor n qubits es un vector en 2n{displaystyle 2^{n} dimensiones. De esta manera, un registro de n cubitos se pueden medir a 2n{displaystyle 2^{n} estados distintos, similares a cómo un registro n bits clásicos pueden contener 2n{displaystyle 2^{n} estados distintos. A diferencia de los bits de las computadoras clásicas, los estados cuánticos pueden tener amplitudes de probabilidad no cero en múltiples valores mensurables simultáneamente. Esto se llama superposición.
La suma de todas las probabilidades para todos los resultados debe ser siempre igual a 1. Otra manera de decir esto es que el teorema pitagórico se generalizó a C2n{displaystyle mathbb {C} {2}}} que todos los estados cuánticos SilencioΨ Ψ . . {displaystyle Silencioso rangle } con n qubits must satisfy 1=. . x=02n− − 1SilencioaxSilencio2,{textstyle 1=sum ¿Por qué? Donde ax{displaystyle a_{x} es la amplitud de probabilidad para el estado mensurable Silenciox. . {displaystyle ← }. Una interpretación geométrica de esto es que el posible espacio-valor de un estado cuántico SilencioΨ Ψ . . {displaystyle Silencioso rangle } con n cubitos es la superficie de la esfera de unidad en C2n{displaystyle mathbb {C} {2}}} y que las transformaciones unitarias (es decir, las puertas lógicas cuánticas) aplicadas a ella son rotaciones en la esfera. Las rotaciones que las puertas realizan forman el grupo de simetría U(2n). La medición es entonces una proyección probabilística de los puntos en la superficie de esta esfera compleja sobre los vectores base que abarcan el espacio (y etiquetan los resultados).
En muchos casos el espacio está representado como un espacio Hilbert H{displaystyle {Mathcal {H}} más que algunos específicos 2n{displaystyle 2^{n}-dimensional espacio complejo. El número de dimensiones (definidas por los vectores de base, y por lo tanto también los posibles resultados de la medición) es entonces a menudo implicado por los operarios, por ejemplo como el espacio estatal requerido para resolver un problema. En el algoritmo de Grover, Grover nombró este conjunto de vectores de base genérica "la base de datos".
La selección de vectores de base contra los cuales medir un estado cuántico influirá en el resultado de la medición. Vea el cambio de base y la entropía Von Neumann para obtener detalles. En este artículo, siempre usamos el base computacional, lo que significa que hemos etiquetado el 2n{displaystyle 2^{n} vectores de base de un n- Registro de codos Silencio0. . ,Silencio1. . ,Silencio2. . ,⋯ ⋯ ,Silencio2n− − 1. . {displaystyle tención0rangle WordPress1rangle WordPress2cdots habit2^{n}-1rangle }, o utilizar la representación binaria Silencio010. . =Silencio0... ... 002. . ,Silencio110. . =Silencio0... ... 012. . ,Silencio210. . =Silencio0... ... 102. . ,⋯ ⋯ ,Silencio2n− − 1. . =Silencio111... ... 12. . {displaystyle Silencio0_{10}rangle = sufrimiento0dots ################################################################################################################################################################################################################################################################ 01_{2}rangle habit2_{10}rangle = resist0dots 10_{2}ranglecdots habit2^{n}-1rangle = endure111dots 1_{2}rangle }.
En mecánica cuántica, los vectores base constituyen una base ortonormal.
Un ejemplo del uso de una base de medición alternativa se encuentra en el cifrado BB84.
El efecto de la medición en los estados entrelazados

Si dos estados cuánticos (es decir, qubits o registros) están entrelazados (lo que significa que su estado combinado no puede expresarse como un producto tensorial), la medición de un registro afecta o revela el estado del otro registro al colapsar parcial o totalmente su estado también. Este efecto se puede utilizar para el cálculo y se utiliza en muchos algoritmos.
La combinación Hadamard-CNOT actúa sobre el estado cero de la siguiente manera:
- CNOT ()H⊗ ⊗ I)Silencio00. . =()[1000010000010010]()12[111− − 1]⊗ ⊗ [1001]))[1000]=12[1001]=Silencio00. . +Silencio11. . 2{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {} {fnMicrosoft Sans Serif} {0} {0} {b} {fnMicrosoft Sans Serif} {0} {0}b} {fnMicrox} {fnMicrosoft}} {f}fnMicros}fnMicros}}fnMicrox}fnMicrox}}fnMicrox}}fnMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinción* {1} {1end{bmatrix}}={frac {fnMicrosoft Sans Serif}

Este estado resultante es el estado de Bell Silencio00. . +Silencio11. . 2=12[1001]{displaystyle {frac {fnMicrosoft Sans Serif}{sqrt {2}}={frac {1}{sqrt {2} {begin{bmatrix}11end{bmatrix}}} {}} {}}}}}}}}}}}}}}} {. No se puede describir como un producto tensor de dos codos. No hay solución para
- [xSí.]⊗ ⊗ [wz]=[xwxzSí.wSí.z]=12[1001],{begin{bmatrix}yend{bmatrix}otimes {begin{bmatrix}w\\zend{bmatrix}={begin{bmatrix}xw\xz\yw\\\\\yzend{bmatrix}}={frac\\\\\\fnMicrocH0}fnMicrocH0}}}}}}\\fnMicrocH0}}}\\\\\\\\\\\\fnMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMin {1} {sqrt {2} {begin{bmatrix}11end{bmatrix}}}}}
porque, por ejemplo, w debe ser cero y distinto de cero en el caso de xw y yw.
El estado cuántico abarcaciones los dos codos. Esto se llama entanglement. Medir uno de los dos cuartos que componen este estado de Bell resultará en que el otro qubit lógicamente debe tener el mismo valor, ambos deben ser el mismo: O se encontrará en el estado Silencio00. . {displaystyle Silencioso, o en el estado Silencio11. . {displaystyle ← }. Si midemos uno de los codos por ejemplo Silencio1. . {displaystyle ← }, entonces el otro cuarto debe ser Silencio1. . {displaystyle ← }, porque su estado combinado se convirtió en Silencio11. . {displaystyle ← }. La medición de uno de los codos colapsa todo el estado cuántico, que abarca los dos codos.
El estado GHZ es un estado cuántico entrelazado similar que abarca tres o más qubits.
Este tipo de asignación de valores se produce instantáneamente en cualquier distancia y, desde 2018, QUESS lo ha verificado experimentalmente para distancias de hasta 1200 kilómetros. El hecho de que el fenómeno parezca ocurrir instantáneamente en lugar del tiempo que tomaría recorrer la distancia que separa los qubits a la velocidad de la luz se llama paradoja EPR, y en física es una cuestión abierta cómo resolver esto. Originalmente se resolvió renunciando al supuesto del realismo local, pero también han surgido otras interpretaciones. Para obtener más información, consulte los experimentos de prueba de Bell. El teorema de la no comunicación demuestra que este fenómeno no se puede utilizar para la comunicación de información clásica más rápido que la luz.
Medición en registros con qubits entrelazados por pares
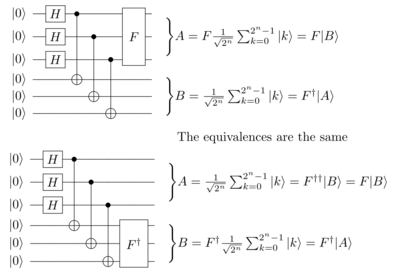
Tome un registro A con n qubits all initialized to Silencio0. . {displaystyle Silencioso, y alimentarlo a través de una puerta paralela Hadamard H⊗ ⊗ n{textstyle H^{otimes No.. Registro A will then enter the state 12n. . k=02n− − 1Silenciok. . {fnK}} {fn}}}be}} - Hola. que tienen igual probabilidad de ser medidos en cualquiera de sus 2n{displaystyle 2^{n} posibles estados; Silencio0. . {displaystyle Silencioso a Silencio2n− − 1. . {displaystyle Ø2n}. Tome un segundo registro B, también con n qubits initialized to Silencio0. . {displaystyle Silencioso y uniforme CNOT sus codos con los codos en el registro A, tal que para cada p los codos Ap{displaystyle A_{p} y Bp{displaystyle B_{p} forma el estado SilencioApBp. . =Silencio00. . +Silencio11. . 2{displaystyle НA_{p}B_{p}rangle ={frac {Sobrevivir00rangle + sobrevivir11rangle }{sqrt {2}}}} {f}}}} {f}}}}}.
Si ahora midemos los qubits en el registro A, entonces el registro B se encontrará para contener el mismo valor que A. Si en cambio aplicamos una puerta lógica cuántica F en A y luego medida, entonces SilencioA. . =FSilencioB. . ⟺ ⟺ F† † SilencioA. . =SilencioB. . {displaystyle TENArangle =F arrestBrangle iff F^{dagger }vivirArangle = pacienciaBrangle, Donde F† † {displaystyle F^{dagger} es el inverso unitario F.
Debido a cómo actúan los inversos unitarios de las puertas, F† † SilencioA. . =F− − 1()SilencioA. . )=SilencioB. . {displaystyle F^{dagger }SobrevivirArangle =F^{-1}(sobrevivirArangle)=. Por ejemplo, digamos F()x)=x+3()mod2n){displaystyle F(x)=x+3{pmod {2}}}Entonces SilencioB. . =SilencioA− − 3()mod2n). . {displaystyle Silencio..
La igualdad se mantendrá sin importar en qué orden se realice la medición (en los registros A o B), suponiendo que F ha llegado a su fin. Las mediciones pueden incluso entrelazarse aleatoria y simultáneamente qubit por qubit, ya que la asignación de mediciones de un qubit limitará el posible espacio de valores de los otros qubits entrelazados.
Aunque se mantienen las igualdades, las probabilidades para medir los posibles resultados pueden cambiar como resultado de aplicar F, al igual que ser la intención de un algoritmo de búsqueda cuántica.
Este efecto de compartir valor a través del entrelazamiento se utiliza en el algoritmo de Shor, la estimación de fase y el conteo cuántico. Usar la transformada de Fourier para amplificar las amplitudes de probabilidad de los estados de solución de algún problema es un método genérico conocido como "pesca de Fourier".
Síntesis de funciones lógicas
Funciones y rutinas que solo usan las puertas pueden describirse como matrices, al igual que las puertas más pequeñas. La matriz que representa una función cuántica actuando en q{displaystyle q} qubits tiene tamaño 2q× × 2q{displaystyle 2^{q}times 2^{q}. Por ejemplo, una función que actúa en un "qubyte" (un registro de 8 qubits) estaría representada por una matriz con 28× × 28=256× × 256{displaystyle 2^{8}times 2^{8}=256times 256} elementos.
Las transformaciones unitarias que no están en el conjunto de puertas nativamente disponibles en el equipo cuántico (las puertas primitivas) pueden ser sintetizadas, o aproximadas, combinando las puertas primitivas disponibles en un circuito. Una manera de hacerlo es factorar la matriz que codifica la transformación unitaria en un producto de productos tensores (es decir, series y circuitos paralelos) de las puertas primitivas disponibles. El grupo U(2q) es el grupo de simetría para las puertas que actúan en q{displaystyle q} Qubits. La factorización es entonces el problema de encontrar un camino en U(2q) del conjunto generador de puertas primitivas. El teorema Solovay-Kitaev muestra que dado un conjunto suficiente de puertas primitivas, existe un eficiente aproximado para cualquier puerta. Para el caso general con un gran número de qubits este enfoque directo a la síntesis de circuitos es intráctil. Esto pone un límite en cómo las funciones grandes pueden ser las fuerzas brutas factorizadas en las puertas cuánticas primitivas. Los programas típicamente cuánticos se construyen usando funciones cuánticas relativamente pequeñas y simples, similares a la programación clásica normal.
Debido a la naturaleza unitaria de las puertas, todas las funciones deben ser reversibles y ser siempre mapas bijetivos de entrada a la salida. Siempre debe existir una función F− − 1{displaystyle F^{-1} tales que F− − 1()F()Silencio↑ ↑ . . ))=Silencio↑ ↑ . . {displaystyle F^{-1}(F(fortpsi rangle)= duraciónpsi rangle }. Las funciones que no son invertibles pueden hacerse invertibles añadiendo codos auxiliares a la entrada o la salida, o ambos. Después de que la función se haya completado, los codos auxiliares pueden entonces ser incomputados o dejados sin tocar. Medir o de otra manera colapsar el estado cuántico de un qubit secundario (por ejemplo, reinicializando el valor de él, o por su decoherencia espontánea) que no se han descompuesto puede resultar en errores, ya que su estado puede estar enredado con los qubits que todavía se utilizan en computaciones.
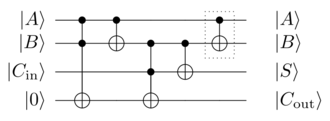
Operaciones lógicamente irreversibles, por ejemplo modulo añadido 2n{displaystyle 2^{n} de dos n{displaystyle n}- Registros de codo a y b, F()a,b)=a+b()mod2n){displaystyle F(a,b)=a+b{pmod {2}}}, se puede hacer lógicamente reversible añadiendo información a la salida, para que la entrada pueda ser calculada de la salida (es decir, existe una función F− − 1{displaystyle F^{-1}). En nuestro ejemplo, esto se puede hacer pasando uno de los registros de entrada a la salida: F()Silencioa. . ⊗ ⊗ Silenciob. . )=Silencioa+b()mod2n). . ⊗ ⊗ Silencioa. . {displaystyle F(prehensiarangle otimes tenciónbrangle)= endurea+b{pmod {2^{n}}}rangle otimes Наrangle }. La salida se puede utilizar para calcular la entrada (es decir, dada la salida a+b{displaystyle a+b} y a{displaystyle a}, podemos encontrar fácilmente la entrada; a{displaystyle a} se da y ()a+b)− − a=b{displaystyle (a+b)-a=b}) y la función se hace bijetivista.
Todas las expresiones algebraicas booleanas se pueden codificar como transformados unitarios (puertas lógicas cuánticas), por ejemplo mediante combinaciones de las puertas Pauli-X, CNOT y Toffoli. Estas puertas están funcionalmente completas en el dominio de la lógica booleana.
Hay muchas transformaciones unitarias disponibles en las bibliotecas de Q#, QCL, Qiskit y otros lenguajes de programación cuántica. También aparece en la literatura.
Por ejemplo, inc()Silenciox. . )=Silenciox+1()mod2xlongitud). . {displaystyle mathrm {inc} (Princexrangle)=tenciónx+1{pmod {2}rangle, donde xlongitud{displaystyle x_{text{length}} es el número de codos que constituye el registro x{displaystyle x}, se implementa como el siguiente en QCL:

cond qufunct inc()qureg x) {} // Registro de incrementos int i; para i = #x-1 a 0 paso -1 {} CNot()x[i] x[0::i]); // aplicar control-no desde } / MSB to LSB}En QCL, el decremento se hace por "deshacer" aumento. El prefijo ! se utiliza para ejecutar el inverso unitario de la función. !inc(x) es el inverso de inc(x) y en su lugar realiza la operación inc† † Silenciox. . =inc− − 1()Silenciox. . )=Silenciox− − 1()mod2xlongitud). . {displaystyle mathrm {inc} {inc} ^{-1}(Principalmentexrangle)= {2}rangle. El cond palabra clave significa que la función puede ser condicional.
En el modelo de computación utilizado en este artículo (el modelo de circuito cuántico), una computadora clásica genera la composición de puertas para la computadora cuántica, y la computadora cuántica se comporta como un coprocesador que recibe instrucciones de la computadora clásica sobre qué puertas primitivas aplicar a qué qubits. La medición de registros cuánticos da como resultado valores binarios que la computadora clásica puede utilizar en sus cálculos. Los algoritmos cuánticos suelen contener una parte clásica y otra cuántica. La E/S no medida (enviar qubits a computadoras remotas sin colapsar sus estados cuánticos) se puede utilizar para crear redes de computadoras cuánticas. Luego, el intercambio de entrelazamiento se puede utilizar para realizar algoritmos distribuidos con computadoras cuánticas que no están conectadas directamente. Ejemplos de algoritmos distribuidos que sólo requieren el uso de un puñado de puertas lógicas cuánticas son la codificación superdensa, el acuerdo bizantino cuántico y el protocolo de intercambio de claves de cifrado BB84.
Contenido relacionado
Física computacional
Ciencia de la información cuántica
BOS/360
Grado de distorsión isócrona
Groff
































































![{displaystyle T={begin{bmatrix}1&0\0&e^{i{frac {pi }{4}}}end{bmatrix}}=Pleft({frac {pi }{4}}right)={sqrt {S}}={sqrt[{4}]{Z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c88bbaf48f6f443648d8e67637a140138ef2cd)









































































































































