Prueba de permutación

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Prueba de hipótesis estadística exacta

A prueba de permutación (también llamada prueba de re-randomización o prueba de shuffle) es una prueba de hipótesis estadística exacta que hace uso de la prueba por contradicción. Una prueba de permutación implica dos o más muestras. La hipótesis nula es que todas las muestras provienen de la misma distribución ${displaystyle H_{0}:F=G}$ . Bajo la hipótesis nula, la distribución de la estadística de prueba se obtiene calculando todos los valores posibles de la estadística de prueba bajo posibles reorganizaciones de los datos observados. Por lo tanto, las pruebas de permutación son una forma de muestreo.

Las pruebas de permutación pueden entenderse como pruebas de datos sustitutos en las que los datos sustitutos bajo la hipótesis nula se obtienen mediante permutaciones de los datos originales.

En otras palabras, el método mediante el cual se asignan los tratamientos a los sujetos en un diseño experimental se refleja en el análisis de ese diseño. Si las etiquetas son intercambiables bajo la hipótesis nula, entonces las pruebas resultantes arrojan niveles de significancia exactos; ver también intercambiabilidad. Luego se pueden derivar intervalos de confianza a partir de las pruebas. La teoría ha evolucionado a partir de los trabajos de Ronald Fisher y E. J. G. Pitman en la década de 1930.

Las pruebas de permutación no deben confundirse con las pruebas aleatorias.

Método

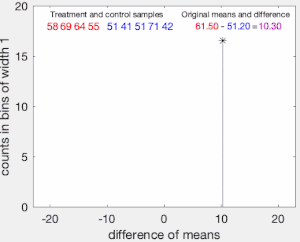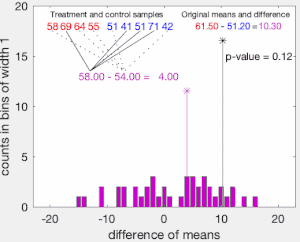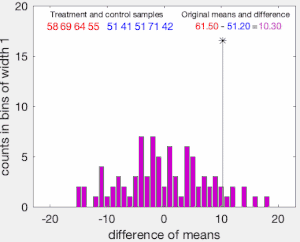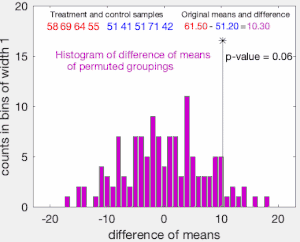
Para ilustrar la idea básica de una prueba de permutación, supongamos que recopilamos variables aleatorias ${displaystyle X_{A}}$ y ${displaystyle X_{B}}$ para cada individuo de dos grupos ${displaystyle A}$ y ${displaystyle B}$ cuyos medios de muestra son ${displaystyle {bar {x}}_{A}}$ y ${displaystyle {bar {x}}_{B}}$ Y que queremos saber si ${displaystyle X_{A}}$ y ${displaystyle X_{B}}$ proviene de la misma distribución. Vamos. ${displaystyle n_{A}}$ y ${displaystyle n_{B}}$ ser el tamaño de la muestra recogido de cada grupo. La prueba de permutación está diseñada para determinar si la diferencia observada entre los medios de muestra es lo suficientemente grande para rechazar, en algún nivel de significación, la hipótesis nula H ${displaystyle _{0}}$ de los datos extraídos ${displaystyle A}$ es de la misma distribución que los datos extraídos ${displaystyle B}$ .

La prueba procede de la siguiente manera. En primer lugar, se calcula la diferencia entre las dos muestras: este es el valor observado de la estadística de prueba, ${displaystyle T_{text{obs}}}$ .

A continuación, las observaciones de los grupos ${displaystyle A}$ y ${displaystyle B}$ se agrupan, y la diferencia en los medios de muestra se calcula y se registra para cada forma posible de dividir los valores agrupados en dos grupos de tamaño ${displaystyle n_{A}}$ y ${displaystyle n_{B}}$ (es decir, por cada permutación de las etiquetas de grupo A y B). El conjunto de estas diferencias calculadas es la distribución exacta de posibles diferencias (para esta muestra) bajo la hipótesis nula de que las etiquetas de grupo son intercambiables (es decir, se asignan al azar).

El valor parcial de la prueba se calcula como la proporción de permutaciones muestreadas en las que la diferencia en los medios era mayor que la ${displaystyle T_{text{obs}}}$ . El valor p-valor de dos caras de la prueba se calcula como la proporción de permutaciones muestradas donde la diferencia absoluta era mayor que la ${displaystyle |T_{text{obs}}|}$ . Muchas implementaciones de pruebas de permutación requieren que los datos observados en sí sean contados como una de las permutaciones para que el valor p-permutación nunca sea cero.

Alternativamente, si el único propósito de la prueba es rechazar o no rechazar la hipótesis nula, uno podría ordenar las diferencias registradas, y luego observar si ${displaystyle T_{text{obs}}}$ está contenido en el centro ${displaystyle (1-alpha)times 100}$ % de ellos, para cierto nivel de significación ${displaystyle alpha }$ . Si no lo es, rechazamos la hipótesis de curvas de probabilidad idénticas en las ${displaystyle alpha times 100%}$ nivel de significación.

Para muestras pareadas, es necesario aplicar la prueba de permutación pareada.

Relación con las pruebas paramétricas

Las pruebas de permutación son un subconjunto de estadísticas no paramétricas. Asumiendo que nuestros datos experimentales provienen de datos medidos de dos grupos de tratamiento, el método simplemente genera la distribución de diferencias medias bajo el supuesto de que los dos grupos no son distintos en términos de la variable medida. A partir de esto, se utiliza entonces la estadística observada ( ${displaystyle T_{text{obs}}}$ arriba) para ver hasta qué punto esta estadística es especial, es decir, la probabilidad de observar la magnitud de tal valor (o mayor) si las etiquetas de tratamiento simplemente se habían aleatorizado después del tratamiento.

En contraste con las pruebas de permutación, las distribuciones que subyacen a muchas pruebas estadísticas populares "clásicas", como la prueba t, F-test, z-test y χ2, se obtienen de distribuciones teóricas de probabilidad. La prueba exacta de Fisher es un ejemplo de una prueba de permutación comúnmente utilizada para evaluar la asociación entre dos variables dicotomosas. Cuando los tamaños de la muestra son muy grandes, la prueba chi-square de Pearson dará resultados precisos. Para las muestras pequeñas, no se puede suponer que la distribución de referencia de la chi-cuadra dé una descripción correcta de la distribución de probabilidad de la estadística de prueba, y en esta situación el uso de la prueba exacta de Fisher se hace más apropiado.

Las pruebas de permutación existen en muchas situaciones donde las pruebas paramétricas no (por ejemplo, cuando se realiza una prueba óptima cuando las pérdidas son proporcionales al tamaño de un error en lugar de su cuadrado). Todas las pruebas paramétricas simples y muchas relativamente complejas tienen una versión de prueba de permutación correspondiente que se define utilizando la misma estadística de prueba como la prueba paramétrica, pero obtiene el valor p de la distribución de permutación de muestra específica de esa estadística, en lugar de la distribución teórica derivada de la suposición paramétrica. Por ejemplo, es posible de esta manera construir una prueba t de permutación, una permutación ${textstyle chi ^{2}}$ prueba de asociación, una versión de permutación de la prueba de Aly para comparar las diferencias y así sucesivamente.

Los principales inconvenientes de las pruebas de permutación son que

Puede ser computacionalmente intensivo y puede requerir código "costo" para estadísticas difíciles de calcular. Esto debe ser reescrito por cada caso.
Se utilizan principalmente para proporcionar un valor p. La inversión de la prueba para conseguir regiones/intervalos de confianza requiere aún más cálculo.

Ventajas

Existen pruebas de permutación para cualquier estadística de prueba, independientemente de si se conoce o no su distribución. Por lo tanto, siempre se es libre de elegir la estadística que mejor discrimine entre hipótesis y alternativa y que minimice las pérdidas.

Las pruebas de permutación se pueden utilizar para analizar diseños desequilibrados y para combinar pruebas dependientes en mezclas de datos categóricos, ordinales y métricos (Pesarin, 2001). También se pueden utilizar para analizar datos cualitativos que han sido cuantificados (es decir, convertidos en números). Las pruebas de permutación pueden ser ideales para analizar datos cuantificados que no satisfacen los supuestos estadísticos subyacentes a las pruebas paramétricas tradicionales (por ejemplo, pruebas t, ANOVA), consulte PERMANOVA.

Antes de la década de 1980, la carga de crear la distribución de referencia era abrumadora, excepto para conjuntos de datos con tamaños de muestra pequeños.

Desde la década de 1980, la confluencia de computadoras rápidas relativamente económicas y el desarrollo de nuevos algoritmos de ruta sofisticados aplicables en situaciones especiales hicieron que la aplicación de métodos de prueba de permutación fuera práctica para una amplia gama de problemas. También inició la incorporación de opciones de pruebas exactas en los principales paquetes de software estadístico y la aparición de software especializado para realizar una amplia gama de pruebas exactas univariables y multivariables y calcular pruebas "exactas" intervalos de confianza.

Limitaciones

Una hipótesis importante detrás de una prueba de permutación es que las observaciones son intercambiables bajo la hipótesis nula. Una consecuencia importante de esta suposición es que las pruebas de diferencia en el lugar (como una prueba t de permutación) requieren la misma variabilidad bajo la suposición de normalidad. En este sentido, el clásico t-test de permutación comparte la misma debilidad que el t-test del estudiante clásico (el problema Behrens-Fisher). Esto se puede abordar de la misma manera que el clásico t-test se ha extendido para manejar diferencias desiguales: empleando la estadística de Welch con el ajuste de Satterthwaite a los grados de libertad. Una tercera alternativa en esta situación es utilizar una prueba basada en arranque. El estatista Phillip Good explica la diferencia entre las pruebas de permutación y las pruebas de arranque de la siguiente manera: "Hipótesis de prueba de permutaciones relativas a distribuciones; hipótesis de prueba de arranque sobre parámetros. Como resultado, el bootstrap implica presunciones menos importantes". Las pruebas de bootstrap no son exactas. En algunos casos, una prueba de permutación basada en una estadística debidamente estudiada puede ser asintoticamente exacta incluso cuando se viola la suposición de intercambiabilidad. Las pruebas basadas en bootstrap pueden probar con la hipótesis nula ${displaystyle H_{0}:Fneq G}$ y, por lo tanto, son adecuados para realizar pruebas de equivalencia.

Pruebas de Montecarlo

Se puede crear una prueba de permutación asintóticamente equivalente cuando hay demasiados ordenamientos posibles de los datos para permitir una enumeración completa de una manera conveniente. Esto se hace generando la distribución de referencia mediante muestreo de Monte Carlo, que toma una muestra aleatoria pequeña (en relación con el número total de permutaciones) de las posibles réplicas. La comprensión de que esto podría aplicarse a cualquier prueba de permutación en cualquier conjunto de datos fue un avance importante en el área de la estadística aplicada. Las primeras referencias conocidas a este enfoque son Eden y Yates (1933) y Dwass (1957). Este tipo de prueba de permutación se conoce con varios nombres: prueba de permutación aproximada, prueba de permutación de Monte Carlo o prueba de permutación aleatoria.

Después ${displaystyle N}$ permutaciones al azar, es posible obtener un intervalo de confianza para el valor p basado en la distribución binomial, ver intervalo de confianza de la proporción binomial. Por ejemplo, si después ${displaystyle N=10000}$ permutaciones al azar se calcula que el valor p ${displaystyle {widehat {p}}=0.05}$ , entonces un intervalo de confianza del 99% para la verdad ${displaystyle p}$ (el que resultaría de probar todas las permutaciones posibles) es ${displaystyle left[{hat {p}}-z{sqrt {frac {0.05(1-0.05)}{10000}}},{hat {p}}+z{sqrt {frac {0.05(1-0.05)}{10000}}}right]=[0.045,0.055]}$ .

Por otra parte, el propósito de estimar el valor p es decidir con más frecuencia si ${displaystyle pleq alpha }$ , donde ${displaystyle scriptstyle alpha }$ es el umbral en el que la hipótesis nula será rechazada (típicamente ${displaystyle alpha =0.05}$ ). En el ejemplo anterior, el intervalo de confianza sólo nos dice que hay aproximadamente un 50% de probabilidad de que el valor p es más pequeño que 0.05, es decir, no está completamente claro si la hipótesis nula debe ser rechazada a nivel ${displaystyle alpha =0.05}$ .

Si sólo es importante saber si ${displaystyle pleq alpha }$ para un determinado ${displaystyle alpha }$ , es lógico continuar simulando hasta la declaración ${displaystyle pleq alpha }$ puede ser establecido para ser verdadero o falso con una probabilidad muy baja de error. Dado un límite ${displaystyle epsilon }$ sobre la probabilidad admisible de error (la probabilidad de encontrar que $alpha }" xmlns="http://www.w3.org/1998/Math/MathML">p^ ^ ■α α {displaystyle {widehat {p}} {alpha}alpha }" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a8352e351fe8de49d36463f09c80ab88767a2153" style="vertical-align: -0.671ex; margin-left: -0.089ex; width:6.035ex; height:2.509ex;"/>$ cuando de hecho ${displaystyle pleq alpha }$ o viceversa), la cuestión de cuántas permutaciones se pueden considerar como la cuestión de cuándo dejar de generar permutaciones, sobre la base de los resultados de las simulaciones hasta ahora, para garantizar que la conclusión (que es o ${displaystyle pleq alpha }$ o $alpha }" xmlns="http://www.w3.org/1998/Math/MathML">p■α α {displaystyle p títuloalpha }alpha }" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4146efa9fa314c8380b44dd655f2fb89f9ae03b3" style="vertical-align: -0.671ex; margin-left: -0.089ex; width:5.845ex; height:2.176ex;"/>$ ) es correcto con probabilidad al menos tan grande como ${displaystyle 1-epsilon }$ . () ${displaystyle epsilon }$ típicamente será elegido para ser extremadamente pequeño, por ejemplo 1/1000.) Se han desarrollado reglas para lograr esto que pueden incorporarse con un coste computacional mínimo. De hecho, dependiendo del verdadero valor p subyacente a menudo se encontrará que el número de simulaciones requeridas es notablemente pequeño (por ejemplo, tan bajo como 5 y a menudo no más de 100) antes de que una decisión se pueda alcanzar con certeza virtual.

Pruebas de ejemplo

Análisis permutacional de la varianza
Producto Rank

Literatura

Referencias originales:

Contenido relacionado

Más resultados...