Prueba de línea horizontal

En matemáticas, la prueba de la línea horizontal es una prueba utilizada para determinar si una función es inyectiva (es decir, uno a uno).

En cálculo

A Línea horizontal es una línea recta y plana que va de izquierda a derecha. Dada la función f:: R→ → R{displaystyle fcolon mathbb {R} to mathbb {R} (es decir, de los números reales a los números reales), podemos decidir si es inyectable mirando líneas horizontales que intersectan el gráfico de la función. Si hay alguna línea horizontal Sí.=c{displaystyle y=c} interseca el gráfico en más de un punto, la función no es inyectable. Para ver esto, note que los puntos de intersección tienen el mismo valor y (porque se encuentran en la línea Sí.=c{displaystyle y=c}) pero diferentes valores x, que por definición significa que la función no puede ser inyectable.

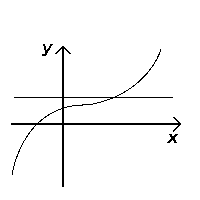Pasa la prueba (inyección)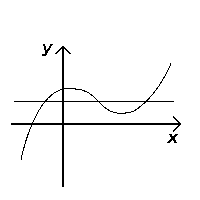

Falla la prueba (no inyectable)

Se pueden usar variaciones de la prueba de la línea horizontal para determinar si una función es sobreyectiva o biyectiva:

• La función f es subjetivo (es decir, a) si y sólo si su gráfico interseca cualquier línea horizontal en mínimo una vez.
• f es bijetivo si y sólo si alguna línea horizontal intersecciona el gráfico exactamente una vez.

En teoría de conjuntos

Considerar una función f:: X→ → Y{displaystyle fcolon Xto Y} con su correspondiente gráfico como subconjunto del producto cartesiano X× × Y{displaystyle Xtimes Y}. Considerar las líneas horizontales X× × Y{displaystyle Xtimes Y}:{}()x,Sí.0)▪ ▪ X× × Y:Sí.0es constante}=X× × {}Sí.0}{displaystyle {(x,y_{0})in Xtimes Y... Xtimes {y_{0}}. La función f es inyectable si y sólo si cada línea horizontal intersecciona el gráfico a la mayor parte de la vez. En este caso se dice que el gráfico pasa la prueba de línea horizontal. Si cualquier línea horizontal intersecciona el gráfico más de una vez, la función falla la prueba de la línea horizontal y no es inyectable.