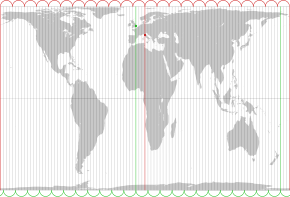
Proyección de Gall-Peters
La proyección de Gall-Peters es una proyección cartográfica rectangular de áreas iguales. Como todas las proyecciones de áreas iguales, distorsiona la mayoría de las formas. Es una proyección cilíndrica de áreas iguales con latitudes 45° norte y sur como las regiones del mapa que no tienen distorsión.
La proyección lleva el nombre de James Gall y Arno Peters. Gall describió la proyección en 1855 en una convención científica y publicó un artículo sobre ella en 1885. Peters llevó la proyección a un público más amplio a principios de la década de 1970 a través de su 'Peters World Map'. El nombre "proyección de Gall-Peters" fue utilizado por primera vez por Arthur H. Robinson en un folleto publicado por la Asociación Cartográfica Estadounidense en 1986.
Los mapas basados en la proyección son promovidos por la UNESCO y también son ampliamente utilizados por las escuelas británicas. El estado de Massachusetts y las Escuelas Públicas de Boston de los EE. UU. comenzaron a incorporar estos mapas en marzo de 2017, convirtiéndose en el primer distrito escolar público y estado de los Estados Unidos en adoptar los mapas de Gall-Peters como estándar.
La proyección de Gall-Peters alcanzó notoriedad a finales del siglo XX como pieza central de una controversia sobre las implicaciones políticas del diseño de mapas.
Descripción
Fórmula
La proyección se define convencionalmente como:
- x=Rπ π λ λ # 45∘ ∘ 180∘ ∘ =Rπ π λ λ 180∘ ∘ 2Sí.=Rpecado φ φ # 45∘ ∘ =R2pecado φ φ {displaystyle {begin{aligned}x limit={frac {Rpi lambda cos 45^{circ ##{180^{circ }={frac {Rpi lambda}{180^{circ} ################################################################################################################################################################################################################################################################ {Rsin varphi }{cos 45^{circu} }=R{sqrt {2}sin varphi end{aligned}}
donde λ es la longitud desde el meridiano central en grados, φ es la latitud y R es el radio del globo utilizado como el modelo de la tierra para la proyección. Para la longitud dada en radianes, elimine π /180° factores.
Fórmula simplificada
Excluyendo la conversión de unidades y el escalado uniforme, las fórmulas se pueden escribir:
- x=Rλ λ Sí.=2Rpecado φ φ {displaystyle {begin{aligned}x limit= Rlambda \y paciente=2Rsin varphi end{aligned}}
Donde λ λ {displaystyle lambda } es la longitud del meridiano central (en radians), φ φ {displaystyle varphi } es la latitud, y R es el radio del globo utilizado como el modelo de la tierra para proyección. De ahí que la esfera se mapee sobre el cilindro vertical, y el cilindro se estira para duplicar su longitud. El factor de estiramiento, 2 en este caso, es lo que distingue las variaciones de la proyección cilíndrica de la misma zona.
Discusión
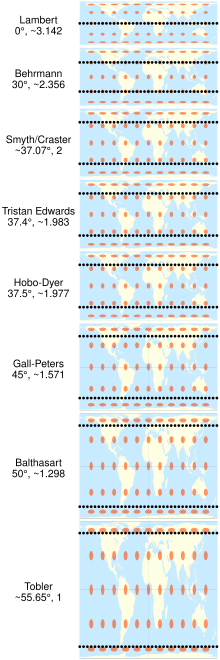
Las diversas especializaciones de la proyección cilíndrica de áreas iguales difieren solo en la relación entre el eje vertical y el horizontal. Esta relación determina el paralelo estándar de la proyección, que es el paralelo en el que no hay distorsión y en el que las distancias coinciden con la escala indicada. Siempre hay dos paralelos estándar en la proyección cilíndrica de áreas iguales, cada uno a la misma distancia al norte y al sur del ecuador. Los paralelos estándar de Gall-Peters son 45° N y 45° S. Se han descrito, promovido o nombrado de otra forma varias otras especializaciones del cilíndrico de áreas iguales.
| Especialización | Paralelos estándar N/S |
|---|---|
| Lambert cylindric equal-area | Ecuador |
| Behrmann cylindric equal-area | 30° |
| Smyth igual-surface (= Craster rectangular) | 37°04′ |
| Trystan Edwards | 37°24′ |
| Hobo-Dyer | 37°30′′ |
| Gall-Peters (= Gall orthographic = Peters) | 45° |
| Balthasart | 50° |
| El mundo de Tobler en un cuadrado | 55°39′ |
Orígenes y nombres
La proyección de Gall-Peters fue descrita por primera vez en 1855 por el clérigo James Gall, quien la presentó junto con otras dos proyecciones en la reunión de Glasgow de la Asociación Británica para el Avance de la Ciencia (BA). Le dio el nombre de "ortográfico" y publicó formalmente su trabajo en 1885 en la Scottish Geographical Magazine. La proyección sugiere la proyección ortográfica en el sentido de que las distancias entre los paralelos de Gall-Peters son un múltiplo constante de las distancias entre los paralelos de la ortográfica. Esa constante es √2.
En 1967, el cineasta alemán Arno Peters ideó de forma independiente una proyección similar, que presentó en 1973 como el 'mapa mundial de Peters'. La descripción original de Peters de su proyección contenía un error geométrico que, tomado literalmente, implica paralelos estándar de 46°02′ N/S. Sin embargo, el texto que acompañaba a la descripción dejaba en claro que pretendía que los paralelos estándar fueran de 45° N/S, lo que hacía que su proyección fuera idéntica a la ortográfica de Gall. En cualquier caso, la diferencia es inapreciable en un mapamundi.
El nombre "proyección de Gall-Peters" parece haber sido utilizado por primera vez por Arthur H. Robinson en un folleto publicado por la Asociación Cartográfica Estadounidense en 1986. Antes de 1973 se conocía, cuando se lo mencionaba, como el "Gall ortográfico" o "Gall's ortográfica." La mayoría de los partidarios de Peters hoy en día se refieren a ella solo como la "proyección de Peters". Durante los años de controversia la literatura cartográfica tendió a mencionar ambas atribuciones, decidiéndose por una u otra a los efectos del artículo. En los últimos años, "Gall–Peters" parece dominar.
Controversia del mapamundi de Peters
La proyección de Gall-Peters inicialmente pasó desapercibida cuando fue presentada por Gall en 1855. Consiguió una mayor atención después de que Arno Peters la reintrodujera en 1973. La promocionó como una alternativa superior a la proyección de Mercator de uso común, sobre la base de que la La proyección de Mercator distorsiona en gran medida los tamaños relativos de las regiones en un mapa. En particular, criticó que la proyección de Mercator hace que las ricas Europa y América del Norte parezcan muy grandes en relación con las más pobres de África y América del Sur. Estos argumentos llevaron a muchos grupos socialmente preocupados a adoptar la proyección de Gall-Peters, incluido el Consejo Nacional de Iglesias y la revista New Internationalist.
Su campaña se vio reforzada por la afirmación inexacta de que la proyección de Gall-Peters era la única "área correcta" mapa. En realidad, algunas de las proyecciones más antiguas son de áreas iguales (como la proyección sinusoidal), y se han descrito cientos. También afirmó incorrectamente que poseía 'conformidad de ángulo absoluto', 'no tenía distorsiones extremas de forma' y era 'totalmente realista a distancia'. Peters enmarcó sus críticas a la proyección de Mercator con críticas a la comunidad cartográfica más amplia. En particular, Peters escribió en La nueva cartografía,
Por la autoridad de su profesión [cartógrafos] han obstaculizado su desarrollo. Desde que Mercator produjo su mapa global hace más de cuatrocientos años para la edad de la dominación mundial europea, los cartógrafos se han aferrado a él a pesar de que ha estado muy obsoleto por los acontecimientos. Han tratado de hacerlo tópico por correcciones cosméticas.... La profesión cartográfica es, por su retención de viejos preceptos basados en el concepto global eurocéntrico, incapaz de desarrollar este mapa mundial igualitario que solo puede demostrar la paridad de todos los pueblos de la tierra.
A medida que las promociones de Peters ganaban popularidad, la comunidad cartográfica reaccionó con hostilidad a sus críticas, así como a la inexactitud y falta de novedad de sus afirmaciones. Llamaron la atención sobre la larga lista de cartógrafos que, durante el siglo anterior, habían expresado formalmente su frustración con los editores' uso excesivo de Mercator y abogó por alternativas. Además, varios académicos criticaron las distorsiones particularmente grandes presentes en la proyección de Gall-Peters y comentaron sobre la ironía de su presentación sin distorsiones de las latitudes medias, incluida la Alemania natal de Peters, a expensas de las latitudes bajas, que albergar más de las naciones tecnológicamente subdesarrolladas.
La creciente publicidad de las afirmaciones de Peter en 1986 motivó a la Asociación Cartográfica Estadounidense (ahora Sociedad de Información Geográfica y Cartografía) a producir una serie de folletos (incluido Qué mapa es mejor) diseñados para educar al público sobre las proyecciones de mapas y la distorsión en los mapas. En 1989 y 1990, después de un debate interno, siete organizaciones geográficas de América del Norte adoptaron una resolución que rechaza todos los mapas del mundo rectangulares, una categoría que incluye tanto las proyecciones de Mercator como las de Gall-Peters, aunque la Sociedad de Información Cartográfica de América del Norte se negó notablemente a respaldarlo..
Los dos bandos nunca hicieron ningún intento real de reconciliación. El campo de Peters ignoró en gran medida las protestas de los cartógrafos y no reconoció el trabajo anterior de Gall hasta que la controversia había seguido su curso en gran medida, al final de la vida de Peters. Si bien es probable que ideó la proyección de forma independiente, su conducta poco académica y su negativa a involucrar a la comunidad cartográfica indudablemente contribuyeron a la polarización y el callejón sin salida.
En las décadas siguientes, J. Brian Harley le dio crédito al fenómeno Peters por demostrar las implicaciones sociales de las proyecciones de mapas, mientras que Jeremy Crampton considera que todos los mapas son políticos y ve la condena de la comunidad cartográfica como reaccionaria y tal vez una demostración de inmadurez. en la profesión
Contenido relacionado
San Bernardino, California
Aotearoa
Condado de Alameda, California