Polígono equiangular

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Poligono con vértices de igual ángulo

Ejemplo de polígonos equiangulares
Direct	Indirect	Skew
Un rectángulo, "Seguido4" es un convex poligonal equiangular directo, conteniendo cuatro ángulos internos de 90°.	Un cóncavo polígono equiangular indirectoComo este hexágono, en sentido contrario, tiene cinco vueltas izquierdas y un giro derecho, como este tetromino.	Un polígono asado tiene ángulos iguales fuera de un plano, como este octógono asado alternando bordes rojos y azules en un cubo.
Direct	Indirect	Contrarrestado
Un polígono equiangular de giro múltiple puede ser directo, como este octógono, <8/2 título, tiene 8 giros 90°, totalizando 720°.	Un polígono equiangular indirecto de cóncava, .5-2 título, en sentido contrario tiene 4 vueltas izquierdas y un giro derecho. (-1.2.4.3.2)_60°	Un hexágono equiangular indirecto, ■6-6 título_90° con 3 vueltas izquierdas, 3 vueltas derechas, totalizando 0°.

En geometría euclidiana, un polígono equiangular es un polígono cuyos ángulos de vértice son iguales. Si las longitudes de los lados también son iguales (es decir, si también es equilátero) entonces es un polígono regular. Los polígonos isogonales son polígonos equiangulares que alternan dos longitudes de aristas.

Para mayor claridad, un polígono equiangular plano se puede llamar directo o indirecto. Un polígono equiangular directo tiene todos los ángulos que giran en la misma dirección en un plano y puede incluir múltiples giros. Los polígonos equiangulares convexos son siempre directos. Un polígono equiangular indirecto puede incluir ángulos que giran hacia la derecha o hacia la izquierda en cualquier combinación. Un polígono equiangular sesgado puede ser isogonal, pero no puede considerarse directo ya que no es plano.

Un n_θ espirolateral es un caso especial de un polígono equiangular con un conjunto de n aristas enteras. longitudes repitiendo secuencia hasta regresar al inicio, con ángulos internos del vértice θ.

Construcción

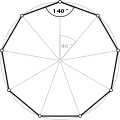
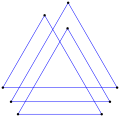
An polígono equiangular se puede construir a partir de un polígono regular o un polígono estrella regular donde los bordes se extienden como líneas infinitas. Cada borde se puede mover de forma independiente perpendicular a la dirección de la línea. Los vértices representan el punto de intersección entre pares de línea vecina. Cada línea movida ajusta su longitud de borde y las longitudes de sus dos bordes vecinos. Si los bordes se reducen a cero longitud, el polígono se degenera, o si se reduce a negativo longitudes, esto revertirá los ángulos internos y externos.

Para un polígono equiangular directo de lados pares, con ángulos internos θ°, mover bordes alternos puede invertir todos los vértices en ángulos suplementarios, 180-θ°. Los polígonos equiangulares directos de lados impares sólo se pueden invertir parcialmente, dejando una mezcla de ángulos suplementarios.

Cada polígono equiangular se puede ajustar en proporciones mediante esta construcción y aún así conservar el estado equiangular.

Este convex hexagonal equiangular directo, <6 contacto, está atado por 6 líneas con ángulo de 60° entre. Cada línea se puede mover perpendicular a su dirección.	Este cóncavo hexagonal equiangular indirecto, <6-2 título, también está atado por 6 líneas con ángulo de 90° entre, cada línea se movió independientemente, moviendo vértices como nuevas intersecciones.

Teorema del polígono equiangular

Para un góndo equiángulo convexo p, cada ángulo interno es 180(1-2/p)°; este es el teorema del polígono equiangular.

Para un polígono estrella p/q equiangular directo, densidad q, cada ángulo interno es 180(1-2q /p)°, con 1<2q<p. Para w=gcd(p,q)>1, esto representa una herida w (p/w)/(q/w) polígono estrella, que es degenerado para el caso normal.

Un equiangular indirecto cóncavo (p_r+p_l)-gon, con p_r vértices de giro a la derecha y p_l vértices de giro a la izquierda, tendrán ángulos internos de 180(1-2/|p_r-p_l|))°, independientemente de su secuencia. Una estrella indirecta equiangular (p_r+p_l)-gon, con p_r vértices de giro a la derecha y p_l vértices de giro a la izquierda y q giros totales, tendrán ángulos internos de 180(1-2q/|p_r-p_l|))° , independientemente de su secuencia. Un polígono equiangular con el mismo número de giros a la derecha y a la izquierda tiene cero giros totales y no tiene restricciones en sus ángulos.

Notación

A cada -gón p equiangular directo se le puede dar una notación <p> o <p/q>, como polígonos regulares {p} y polígonos de estrella regulares {p/ q}, que contiene p vértices y estrellas con densidad q.

Gones p convexos equiangulares <p> tienen ángulos internos de 180(1-2/p)°, mientras que los polígonos equiangulares de estrella directa, <p/q>, tienen ángulos internos ángulos 180(1-2q/p)°.

A un góndo p equiangular indirecto cóncavo se le puede dar la notación <p-2c>, con c vértices de contragiro. Por ejemplo, <6-2> es un hexágono con ángulos internos de diferencia de 90°, <4>, 1 vértice contragirado. A un p-gón equilátero indirecto de múltiples vueltas se le puede dar la notación <^p-2c/_q> con vértices de contragiro c y giros totales q. Un polígono equiangular <p-p> es un p-gón con ángulos internos indefinidos θ, pero se puede expresar explícitamente como <p-p>_θ.

Otras propiedades

El teorema de Viviani se cumple para polígonos equiangulares:

La suma de distancias desde un punto de interior a los lados de un polígono equiangular no depende de la ubicación del punto, y es que el polígono invariante.

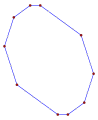
Un polígono cíclico es equiangular si y sólo si los lados alternos son iguales (es decir, los lados 1, 3, 5,... son iguales y los lados 2, 4,... son iguales). Así, si n es impar, un polígono cíclico es equiangular si y sólo si es regular.

Para el p primo, todo -gón p equiangular de lados enteros es regular. Además, cada p^k-gón equiangular de lados enteros tiene simetría rotacional p-fold.

Un conjunto ordenado de longitudes laterales ${displaystyle (a_{1},dotsa_{n})}$ da lugar a un equiangular n- si y sólo si cualquiera de dos condiciones equivalentes tiene para el polinomio ${displaystyle a_{1}+a_{2}x+cdots +a_{n-1}x^{n-2}+a_{n}x^{n-1}:}$ equivale a cero en el valor complejo ${displaystyle e^{2pi i/n};}$ es divisible por ${displaystyle x^{2}-2xcos(2pi /n)+1.}$

Polígonos equiangulares directos por lados

Los polígonos equiangulares directos pueden ser simetrías regulares, isogonales o inferiores. Ejemplos de <p/q> están agrupados en secciones por p y subgrupos por densidad q.

Triángulos equiángulos

Los

triángulos equiangulares deben ser convexos y tener ángulos internos de 60°. Es un triángulo equilátero y un triángulo regular, <3>={3}. El único grado de libertad es la longitud del borde.

Regular, {3}, r₆

Cuadriláteros equiángulos

Un rectángulo disecado en una matriz de 2×3 de cuadrados

Los cuadriláteros equiangulares directos tienen ángulos internos de 90°. Los únicos cuadriláteros equiangulares son los rectángulos, <4>, y los cuadrados, {4}.

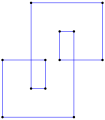
Un cuadrilátero equiangular con longitudes de lados enteras se puede revestir con cuadrados unitarios.

Regular, {4}, r₈
Spirolateral 2_90°, p₄

Pentágonos equiangulares

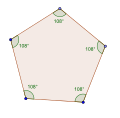
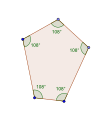
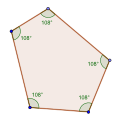
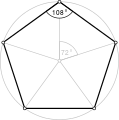
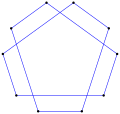
Pentágonos equiángulos directos, <5> y <5/2>, tienen ángulos internos de 108° y 36° respectivamente.

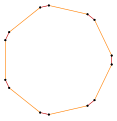
Angulo interno 108° desde un pentágono equiangular,

Los pentágonos equiangulares pueden ser regulares, tener simetría bilateral o no tener simetría.

Regular, r₁₀
Simetría bilateral, i₂
Sin simetría, una₁

ángulos internos de 36° desde un pentagrama equiangular,

pentagrama regular, r₁₀
Irregular, d₂

Hexágonos equiangulares

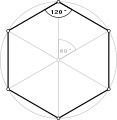
Direct hexágonos equiangulares, не6 contacto y י6/2 título, tienen ángulos internos de 120° y 60° respectivamente.

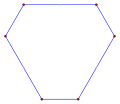
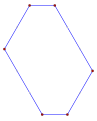
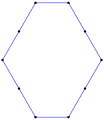
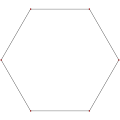
ángulos internos de 120° de un hexágono equiangular,

Un hexágono equiangular con longitudes de lados enteras se puede revestir con triángulos equiláteros unitarios.

Regular, {6}, r₁₂
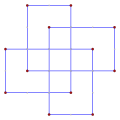
Spirolateral (1,2)_120°, p₆
Spirolateral (1...3)_120°, g₂
Spirolateral (1,2,2)_120°, yo₄
Spirolateral (1,2,2,2,1,3)_120°, p₂

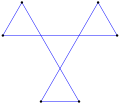
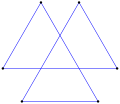
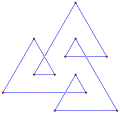
ángulos internos de 60° de un triángulo de doble hila equiangular,

Regular, degenerado, r₆
Spirolateral (1,3)_60°, p₆
Spirolateral (1,2)_60°, p₆
Spirolateral (2,3)_60°, p₆
Spirolateral (1,2,3,4,3,2)_60°, p₂

Heptágonos equiangulares

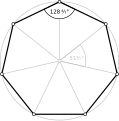
Heptágonos equiangulares directos, <7>, <7/2> y <7/3> tienen ángulos internos de 128 4/7°, 77 1/7° y 25 5/7° respectivamente.

128.57° ángulos internos de un heptógono equiangular, ▪7 título

Regular, {7}, r₁₄
Irregular, i₂

77,14° ángulos internos de un heptagrama equiangular,

Regular, r₁₄
Irregular, i₂

25,71° ángulos internos de un heptagrama equiangular,

Regular, r₁₄
Irregular, i₂

Octágonos equiangulares

octágonos equiangulares directos, <8>, <8/2> y <8/3>, tienen ángulos internos de 135°, 90° y 45° respectivamente.

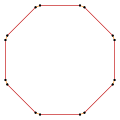
135° ángulos internos desde un octógono equiangular,

Regular, r₁₆
Spirolateral (1,2)_135°, p₈
Spirolateral (1...4)_135°, g₂
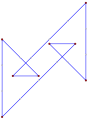
cuadrado sin igual truncado, p₂

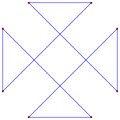
90° ángulos internos desde un cuadrado de doble hilado equiangular, iere8/2

Degenerado regular, r₈
Spirolateral (1,2,2,3,2,2,1)_90°, d₂
Spirolateral (2,1,3,2,3,1,2)_90°, d₂

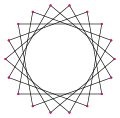
ángulos internos de 45° desde un octagrama equiangular,

Regular, r₁₆
Isogonal, p₈
Isogonal, p₈
Spirolateral, (1,2)_45°, p₈
Isogonal, p₈
Spirolateral (1...4)_45°, g₂

Eneágonos equiangulares

Eneágonos equiangulares directos, <9>, <9/2>, <9/3> y <9/4> Tienen ángulos internos de 140°, 100°, 60° y 20° respectivamente.

Angulos internos de 140° desde un enagón equiangular ▪9 título

Regular, r₁₈
Spirolateral (1,1,3)_140°, yo₆

Ángulos internos de 100° desde un enneagrama equiangular,

Regular {9/2}, p₉
Spirolateral (1,1,5)_100°, yo₆
Spirolateral 3_100°, g₃

ángulos internos de 60° desde un equiangular triángulo tridimensional, ■9/3

Regular, degenerado, r₆
Irregular, a₁
Irregular, a₁
Irregular, a₁

20° ángulos internos a partir de un enneagrama equiangular,

Regular {9/4}, r₁₈
Spirolateral 3_20°, g₃
Irregular, i₂

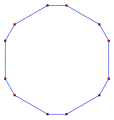
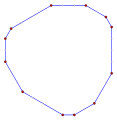
Decágonos equiangulares

Los decágonos equiangulares directos, <10>, <10/2>, <10/3>, <10/4>, tienen 144°, 108°, 72° y Ángulos internos de 36° respectivamente.

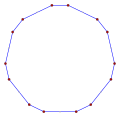
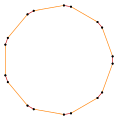
Ángulos internos de 144° desde un decagon equiangular

Regular, r₂₀
Spirolateral (1,2)_144°, p₁₀
Spirolateral (1...5)_144°, g₂

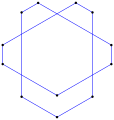
108° ángulos internos desde un pentágono de doble hila equiangular

Regular, degenerado
Spirolateral (1,2)_108°, p₁₀
Irregular, p₂

ángulos internos de 72° desde un decagrama equiangular

Regular {10/3}, r₂₀
Isogonal, p₁₀
Spirolateral (1,2)_72°, p₁₀
Irregular, i₄
Spirolateral (1...5)_72°, g₂

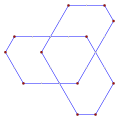
36° ángulos internos de un pentagrama de doble hila equiangular

Regular, degenerado, r₁₀
Spirolateral (1,2)_36°, p₁₀
Isogonal, p₁₀
Isogonal, p₁₀
Irregular, p₂
Irregular, p₂
Irregular, p₂

Hendecagones equiangulares

hendecágonos equiangulares directos, <11>, <11/2>, <11/3>, <11/4> y <11/5> tienen 147 3/11°, 114 6/11°, 81 9/11°, 49 1/11° y 16 4/11° ángulos internos respectivamente.

147° ángulos internos desde un hendecagón equiangular, <11

Regular, {11}, r₂₂

114° ángulos internos de un hendecagrama equiangular, <11/2

Regular {11/2}, r₂₂

ángulos internos de 81° desde un hendecagrama equiangular,

Regular {11/3}, r₂₂

ángulos internos de 49° desde un hendecagrama equiangular,

Regular {11/4}, r₂₂

ángulos internos de 16° desde un hendecagrama equiangular,

Regular {11/5}, r₂₂

Dodecágonos equiangulares

Direct dodecagones equiangulares, не12 caracteres, нет12/2 título, некали, некантеки, y неликиманимениманимен, 120°, 90°, 60° y 30° ángulos internos respectivamente.

150° ángulos internos desde un dodecagón equiangular,

Las soluciones convexas con longitudes de borde entero pueden ser teñidas por bloques de patrón, cuadrados, triángulos equiláteros, y 30° rhombi.

Regular, {12}, r₂₄
Isogonal, p₁₂
Spirolateral (1,2)_150°, p₁₂
Spirolateral (1...3)_150°, g₄
Spirolateral (1...4)_150°, g₃
Spirolateral (1...6)_150°, g₂

Angulos internos de 120° desde un equiangular hexágono doble, ■12/2

Degenerado regular, r₁₂
Spirolateral, (1...4)_120°, g₃
Irregular, d₂
Irregular, d₂

90° ángulos internos desde un equiangular cuadrado de tres kilos, י12/3

Regular, degenerado, r₈
Spirolateral (1...3)_90°, g₂
Spirolateral (2...4)_90°, g₄
Spirolateral (1,1,3)_90°, yo₈
Spirolateral (1,2,2)_90°, yo₈
Spirolateral (1...6)_90°, g₂
Irregular, a₁

ángulos internos de 60° desde un equiangular triángulo cuádruple-wound, ■12/4

Regular, degenerado, r₆
Spirolateral (1,3,5,1)_60°, p₆
Spirolateral (1...4)_60°, g₃
Irregular, a₁

30° ángulos internos desde un equiangular dodecagram, י12/5

Regular {12/5}, r₂₄
Isogonal, p₁₂
Spirolateral (1,2)_30°, p₁₂
Spirolateral (1...3)_30°, g₄
Spirolateral (1...4)_30°, g₃
Spirolateral (1...6)_30°, g₂

Tetradecágonos equiangulares

tetradecágonos equiangulares directos, <14>, <14/2>, <14/3>, <14/4>, y <14/5>, < 14/6>, tienen ángulos internos de 154 2/7°, 128 4/7°, 102 6/7°, 77 1/7°, 51 3/7° y 25 5/7° respectivamente.

154.28° ángulos internos de un tetradecagón equiangular,

Regular {14}, r₂₈
Isogonal, t{7}, p₁₄

128.57° ángulos internos de un hepágono normal de doble hilera equiangular,

Degenerado regular, r₁₄
Isogonal, t{7/2}, p₁₄
Spirolateral 2_128,57°

Ángulos internos 102.85° desde un tetradecagrama equiangular,

Regular {14/3}, r₂₈
Isogonal t{7/3}, p₁₄

77.14° ángulos internos de un heptagrama de doble hilera equiangular

Degenerado regular, r₁₄
Isogonal, p₁₄
Isogonal, p₁₄
Spirolateral 2_77,14°

51,43° ángulos internos de un tetradecagrama equiangular,

Regular {14/5}, r₂₈
Isogonal, p₁₄
Isogonal, p₁₄

25.71° ángulos internos de un heptagrama de doble hilera equiangular,

Degenerado regular, r₁₄
Isogonal, p₁₄
Isogonal, p₁₄
Isogonal, p₁₄
Irregular, d₂

Pentadecágono equiangular

pentadecágonos equiangulares directos, <15>, <15/2>, <15/3>, <15/4>, <15/5>, <15 /6> y <15/7>, tienen ángulos internos de 156°, 132°, 108°, 84°, 60° y 12° respectivamente.

Ángulos internos de 156° desde un pentadecagón equiangular,

Regular, {15}, r₃₀

132° ángulos internos de un pentadecagrama equiangular, iere15/2

Regular, {15/2}, r₃₀

108° ángulos internos de un pentágono tridular equiangular,

Regular, degenerado, r₁₀
spirolateral (1...3)_108°, g₅

Ángulos internos de 84° desde un pentadecagrama equiangular,

Regular, {15/4}, r₃₀

ángulos internos de 60° desde un triángulo equiangular de 5 kilos,

Regular, degenerado, r₆
Irregular, a₁

ángulos internos de 36° desde un pentagrama tridular equiangular,

Regular, degenerado, r₁₀
Irregular, a₁
Spirolateral (1...4)_36°, g₅

12° ángulos internos de un pentadecagrama equiangular, iere15/7

Regular, {15/7}, r₃₀

Hexadecágonos equiangulares

hexadecágonos equiangulares directos, <16>, <16/2>, <16/3>, <16/4>, <16/5>, <16 /6> y <16/7>, tienen ángulos internos de 157,5°, 135°, 112,5°, 90°, 67,5°, 45° y 22,5° respectivamente.

157,5° ángulos internos de un hexadecagón equiangular,

Regular, {16}, r₃₂
Isogonal, t{8}, p₁₆
Spirolateral (1...4)_157,5°, g₄

135° ángulos internos desde un octógono de doble hila equiangular,

Regular, degenerado, r₁₆
Irregular, p₁₆

Ángulos internos de 112,5° desde un hexadecagrama equiangular,

Regular, {16/3}, r₃₂

90° ángulos internos desde un cuadrado equiangular de 4 kilos,

Regular, degenerado, r₈
Irregular, a₁

67,5° ángulos internos de un hexadecagrama equiangular,

Regular, {16/5}, r₃₂

45° ángulos internos de un octagrama regular de doble hilero equiangular,

Regular, degenerado, r₁₆
spirolateral (1...3)_45°, g₈

22,5° ángulos internos de un hexadecagrama equiangular,

Regular, {16/7}, r₃₂
Isogonal, p₁₆

Octadecagones equiangulares

octadecágonos equiangulares directos, <18}, <18/2>, <18/3>, <18/4>, <18/5>, <18 /6>, <18/7> y <18/8>, tienen ángulos internos de 160°, 140°, 120°, 100°, 80°, 60°, 40° y 20° respectivamente.

Ángulos internos de 160° desde un octadecagón equiangular,

Regular, {18}, r₃₆
Isogonal, t{9}, p₁₈

Angulos internos de 140° desde un enneagon equiangular de doble hila,

Regular, degenerado
Spirolateral 2_140°, p₁₈

120° ángulos internos de un hexágono equiangular de 3 libras

Regular, degenerado, r₁₈
irregular, a₁

100° ángulos internos de un enneagrama equiangular de doble hilera

Regular, degenerado, r₁₈
Spirolateral 2_100°, g₃

80° ángulos internos de un octadecagrama equiangular {18/5}

Regular, {18/5}, r₃₆

60° ángulos internos de un triángulo equiangular de 6 libras

Regular, degenerado, r₆
irregular, a₁

40° ángulos internos de un octadecagrama equiangular

Regular, {18/7}, r₃₆
Isogonal, p₁₈
Isogonal, p₁₈
Isogonal, p₁₈

20° ángulos internos de un enneagrama equiangular de doble herida

Regular, degenerado, r₁₈
Isogonal, p₁₈
Isogonal, p₁₈
Isogonal, p₁₈
Isogonal, p₁₈
Spirolateral 2_20°, p₁₈
Spirolateral 6_20°, g₃

Equiangular icosagons

icoságono equiangular directo, <20>, <20/3>, <20/4>, <20/5>, <20/6>, <20 /7> y <20/9>, tienen ángulos internos de 162°, 126°, 108°, 90°, 72°, 54° y 18° respectivamente.