Perpendicular

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Relación entre dos líneas que se encuentran en un ángulo recto (90 grados)

El segmento AB es perpendicular al CD del segmento porque los dos ángulos que crea (indicados en naranja y azul) son cada 90 grados. El segmento AB se puede llamar el perpendicular de A al segmento CD, usando "perpendicular" como sustantivo. El punto B se llama pie del perpendicular desde A CD de serie, o simplemente, el pie de A en CD.

En geometría elemental, dos objetos geométricos son perpendiculares si se intersecan en un ángulo recto (90 grados o π/2 radianes). La condición de perpendicularidad puede representarse gráficamente mediante el símbolo de perpendicularidad, ⟂. Se puede definir entre dos rectas (o dos segmentos de recta), entre una recta y un plano, y entre dos planos.

La perpendicularidad es una instancia particular del concepto matemático más general de ortogonalidad; la perpendicularidad es la ortogonalidad de los objetos geométricos clásicos. Así, en matemáticas avanzadas, la palabra "perpendicular" se utiliza a veces para describir condiciones de ortogonalidad geométrica mucho más complicadas, como la que existe entre una superficie y su vector normal.

Definiciones

Se dice que una recta es perpendicular a otra recta si las dos rectas se intersecan en ángulo recto. Explícitamente, una primera línea es perpendicular a una segunda línea si (1) las dos líneas se encuentran; y (2) en el punto de intersección, el ángulo recto de un lado de la primera línea es cortado por la segunda línea en dos ángulos congruentes. Se puede demostrar que la perpendicularidad es simétrica, lo que significa que si una primera línea es perpendicular a una segunda línea, entonces la segunda línea también es perpendicular a la primera. Por esta razón, podemos hablar de dos líneas como perpendiculares (entre sí) sin especificar un orden. Un gran ejemplo de perpendicularidad se puede ver en cualquier brújula, fíjate en los puntos cardinales; Norte, Este, Sur, Oeste (NESW) La línea N-S es perpendicular a la línea W-E y los ángulos N-E, E-S, S-W y W-N son todos de 90° entre sí.

La perpendicularidad se extiende fácilmente a segmentos y rayos. Por ejemplo, un segmento de línea ${overline {AB}}$ es perpendicular a un segmento de línea ${overline {CD}}$ si, cuando cada uno se extiende en ambas direcciones para formar una línea infinita, estas dos líneas resultantes son perpendiculares en el sentido anterior. En símbolos, ${overline {AB}}perp {overline {CD}}$ significa segmento de línea AB es perpendicular a CD de segmento de línea.

Se dice que una recta es perpendicular a un plano si es perpendicular a todas las rectas del plano que interseca. Esta definición depende de la definición de perpendicularidad entre líneas.

Se dice que dos planos en el espacio son perpendiculares si el ángulo diedro en el que se encuentran es un ángulo recto.

Pie de una perpendicular

La palabra pie se usa con frecuencia en relación con las perpendiculares. Este uso se ejemplifica en el diagrama superior, arriba, y su leyenda. El diagrama puede estar en cualquier orientación. El pie no está necesariamente en la parte inferior.

Más precisamente, sea $A$ un punto y $m$ una línea. Si $B$ es el punto de intersección de $m$ y la línea única a través de $A$ que es perpendicular a $m$ , entonces $B$ se denomina pie de esta perpendicular a través de $A$ .

Construcción de la perpendicular

Construcción del perpendicular (azul) a la línea AB a través del punto P.

Construcción del perpendicular a la media línea h desde el punto P (aplicable no sólo en el punto final A, M es libremente seleccionable), animación al final con pausa 10 s

Para hacer la perpendicular a la línea AB a través del punto P utilizando la construcción de compás y regla, proceda de la siguiente manera (vea la figura de la izquierda):

Paso 1 (rojo): construir un círculo con centro en P para crear puntos A' y B' en la línea AB, que son equidistas de P.
Paso 2 (verde): construir círculos centrados en A' y B' teniendo igual radio. Que Q y P sean los puntos de intersección de estos dos círculos.
Paso 3 (azul): conectar Q y P para construir el PQ perpendicular deseado.

Para demostrar que PQ es perpendicular a AB, utilice el teorema de congruencia SSS para QPA' y QPB' para concluir que los ángulos OPA' y OPB' son iguales. Luego use el teorema de congruencia SAS para los triángulos OPA' y OPB' para concluir que los ángulos POA y POB son iguales.

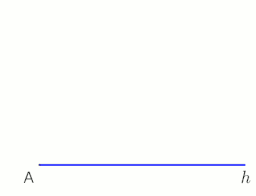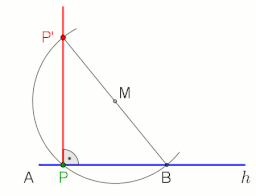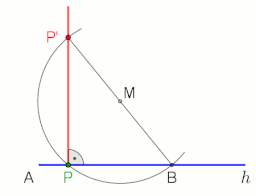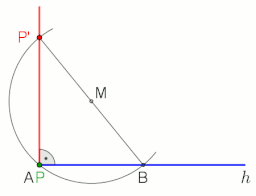
Para hacer la perpendicular a la línea g en o a través del punto P usando el teorema de Thales, vea la animación a la derecha.

El teorema de Pitágoras se puede utilizar como base de métodos para construir ángulos rectos. Por ejemplo, al contar eslabones, se pueden hacer tres piezas de cadena con longitudes en la proporción 3:4:5. Estos se pueden colocar para formar un triángulo, que tendrá un ángulo recto opuesto a su lado más largo. Este método es útil para diseñar jardines y campos, donde las dimensiones son grandes y no se necesita una gran precisión. Las cadenas se pueden utilizar repetidamente cuando sea necesario.

En relación con rectas paralelas

Las marcas de punta de flecha indican que las líneas a y b, cortada por la línea transversal c, son paralelos.

Si dos líneas (a y b) son ambas perpendiculares a una tercera línea (c), todos los ángulos formados a lo largo de la la tercera línea son los ángulos rectos. Por lo tanto, en la geometría euclidiana, dos líneas cualesquiera que sean ambas perpendiculares a una tercera línea son paralelas entre sí, debido al postulado de las paralelas. Por el contrario, si una línea es perpendicular a una segunda línea, también es perpendicular a cualquier línea paralela a esa segunda línea.

En la figura de la derecha, todos los ángulos sombreados en naranja son congruentes entre sí y todos los ángulos sombreados en verde son congruentes entre sí, porque los ángulos verticales son congruentes y los ángulos alternos interiores formados por un corte transversal las rectas paralelas son congruentes. Por lo tanto, si las líneas a y b son paralelas, cualquiera de las siguientes conclusiones conduce a todas las demás:

Uno de los ángulos del diagrama es un ángulo recto.
Uno de los ángulos de afeitado anaranjado es congruente con uno de los ángulos de afeitado verde.
Línea c es perpendicular a la línea a.
Línea c es perpendicular a la línea b.

En cálculo de distancias

En geometría, la distancia perpendicular entre dos objetos es la distancia de uno a otro, medida a lo largo de una línea perpendicular a uno o ambos.

La distancia de un punto a una línea es la distancia al punto más cercano en esa línea. Ese es el punto en el que un segmento de ella al punto dado es perpendicular a la línea.

Asimismo, la distancia de un punto a una curva es medida por un segmento de línea perpendicular a una línea tangente a la curva en el punto más cercano de la curva.

La distancia de un punto a un plano se mide como la longitud desde el punto a lo largo de un segmento que es perpendicular al plano, lo que significa que es perpendicular a todas las líneas en el plano que pasan por el punto más cercano en el plano hasta el punto dado.

Otros casos incluyen:

Punto en avión más cercano al origen, para la distancia perpendicular del origen a un plano en espacio tridimensional
Distancia más cercana entre líneas de sierra, para la distancia perpendicular entre dos líneas no paralelas en el espacio tridimensional

La regresión perpendicular encaja en una línea a los puntos de datos minimizando la suma de distancias perpendiculares cuadradas de los puntos de datos a la línea. Otros métodos de ajuste de curva geométrica utilizando distancia perpendicular para medir la calidad de un ajuste existen, como en total menos cuadrados.

El concepto de distancia perpendicular puede ser generalizado a

distancia ortogonal, entre objetos ortogonales no geométricos más abstractos, como en álgebra lineal (por ejemplo, análisis de componentes principales);
distancia normal, que implica una superficie normal, entre un punto arbitrario y su pie sobre la superficie. Se puede utilizar para la fijación superficial y para definir superficies offset.

Gráfica de funciones

En el plano bidimensional, dos rectas intersecadas pueden formar ángulos rectos si el producto de sus pendientes es igual a −1. Definiendo así dos funciones lineales: $y 1 = a 1 x + b 1$ y $y 2 = a 2 x + b 2$ , las gráficas de las funciones serán perpendiculares y formarán cuatro ángulos rectos donde las líneas se intersecan si $a 1 a 2 = -1$ . Sin embargo, este método no se puede utilizar si la pendiente es cero o indefinida (la línea es paralela a un eje).

Para otro método, sean las dos funciones lineales: $a 1 x + b 1 y + c 1 = 0$ y $a 2 x + b 2 y + c 2 = 0$ . Las líneas serán perpendiculares si y solo si $a 1 a 2 + b 1 b 2 = 0$ . Este método se simplifica a partir del producto escalar (o, más generalmente, el producto interior) de vectores. En particular, dos vectores se consideran ortogonales si su producto interno es cero.

En círculos y otras cónicas

Círculos

Cada diámetro de un círculo es perpendicular a la línea tangente a ese círculo en el punto donde el diámetro interseca al círculo.

Un segmento de línea que pasa por el centro de un círculo y biseca una cuerda es perpendicular a la cuerda.

Si la intersección de dos cuerdas perpendiculares cualesquiera divide una cuerda en longitudes a y b y divide la otra cuerda en longitudes c y d, luego a² + b² + c² + d² es igual al cuadrado del diámetro.

La suma de las longitudes al cuadrado de dos cuerdas perpendiculares cualesquiera que se cortan en un punto dado es la misma que la de otras dos cuerdas perpendiculares que se cortan en el mismo punto, y está dada por 8r² – 4p² (donde r es el radio del círculo y p es la distancia desde el punto central hasta el punto de intersección).

Thales' El teorema establece que dos líneas que pasan por el mismo punto en un círculo pero que pasan por extremos opuestos de un diámetro son perpendiculares. Esto es equivalente a decir que cualquier diámetro de un círculo subtiende un ángulo recto en cualquier punto del círculo, excepto en los dos extremos del diámetro.

Elipses

Los ejes mayor y menor de una elipse son perpendiculares entre sí y a las líneas tangentes a la elipse en los puntos donde los ejes se cruzan con la elipse.

El eje mayor de una elipse es perpendicular a la directriz ya cada lado recto.

Parábolas

En una parábola, el eje de simetría es perpendicular a cada uno de los latus rectum, la directriz y la línea tangente en el punto donde el eje interseca a la parábola.

Desde un punto de la recta tangente al vértice de una parábola, la otra recta tangente a la parábola es perpendicular a la recta que parte de ese punto y pasa por el foco de la parábola.

La propiedad ortóptica de una parábola es que si dos tangentes a la parábola son perpendiculares entre sí, entonces se cortan en la directriz. Por el contrario, dos tangentes que se cortan en la directriz son perpendiculares. Esto implica que, vista desde cualquier punto de su directriz, toda parábola subtiende un ángulo recto.

Hipérbolas

El eje transversal de una hipérbola es perpendicular al eje conjugado ya cada directriz.

El producto de las distancias perpendiculares desde un punto P en una hipérbola o en su hipérbola conjugada a las asíntotas es una constante independiente de la ubicación de P.

Una hiperbola rectangular tiene asintotos que son perpendiculares entre sí. Tiene una excentricidad igual a ${sqrt {2}}.$

En polígonos

Triángulos

Los catetos de un triángulo rectángulo son perpendiculares entre sí.

Las alturas de un triángulo son perpendiculares a sus respectivas bases. Las bisectrices perpendiculares de los lados también juegan un papel destacado en la geometría del triángulo.

La línea de Euler de un triángulo isósceles es perpendicular a la base del triángulo.

El teorema de la línea de Droz-Farny se refiere a una propiedad de dos líneas perpendiculares que se cruzan en el ortocentro de un triángulo.

El teorema de Harcourt se refiere a la relación de los segmentos de recta a través de un vértice y perpendiculares a cualquier recta tangente a la circunferencia inscrita del triángulo.

Cuadriláteros

En un cuadrado u otro rectángulo, todos los pares de lados adyacentes son perpendiculares. Un trapezoide recto es un trapezoide que tiene dos pares de lados adyacentes que son perpendiculares.

Cada una de las cuatro maltitudes de un cuadrilátero es una perpendicular a un lado que pasa por el punto medio del lado opuesto.

Un cuadrilátero ortodiagonal es un cuadrilátero cuyas diagonales son perpendiculares. Estos incluyen el cuadrado, el rombo y la cometa. Por el teorema de Brahmagupta, en un cuadrilátero ortodiagonal que también es cíclico, una línea que pasa por el punto medio de un lado y por el punto de intersección de las diagonales es perpendicular al lado opuesto.

Según el teorema de van Aubel, si los cuadrados se construyen externamente sobre los lados de un cuadrilátero, los segmentos de línea que conectan los centros de los cuadrados opuestos son perpendiculares y de igual longitud.

Líneas en tres dimensiones

Hasta tres líneas en un espacio tridimensional pueden ser pares perpendiculares, como lo ejemplifican los ejes x, y y z de un sistema de coordenadas cartesianas tridimensional.

Contenido relacionado

Más resultados...