Permitividad relativa

La permitividad relativa es la medida de la capacidad de un material aislante para almacenar energía eléctrica en un campo eléctrico, respecto del vacío. Esta, se define como la relación entre la permitividad del material (ε) y la permitividad del vacío (ε₀) ε / ε₀. Así, la permitividad relativa mide la capacidad de los materiales dieléctricos (aislantes) para almacenar energía eléctrica dentro de un campo eléctrico. En algunos textos se conoce como constante dieléctrica.

Podemos entender la permitividad relativa como el factor que reduce la fuerza de Coulomb entre dos cargas puntuales cuando se encuentran dentro de un material (permitividad), a diferencia de lo que pasaría si se encontraran en el vacío (permitividad relativa). La permitividad relativa de un material para una frecuencia de cero se conoce como su permisividad relativa estática.

Además, es directamente proporcional a la capacitancia de un condensador que utilice ese material como dieléctrico. En otras palabras, si un condensador utiliza un material con alta permitividad relativa, tendrá una mayor capacidad para almacenar carga que un condensador idéntico con el vacío como material dieléctrico.

El término histórico para la permitividad relativa es constante dieléctrica. Todavía se usa comúnmente, pero las organizaciones de estándares lo han desaprobado debido a su ambigüedad, ya que algunos informes anteriores lo usaban también para la permitividad absoluta ε. La permitividad puede usarse como una propiedad estática o como una variante dependiente de la frecuencia, en cuyo caso también se conoce como función dieléctrica. También se ha utilizado para referirse únicamente al componente real ε'_r de la permitividad relativa de valores complejos.

HSD

Fórmula de la permitividad relativa

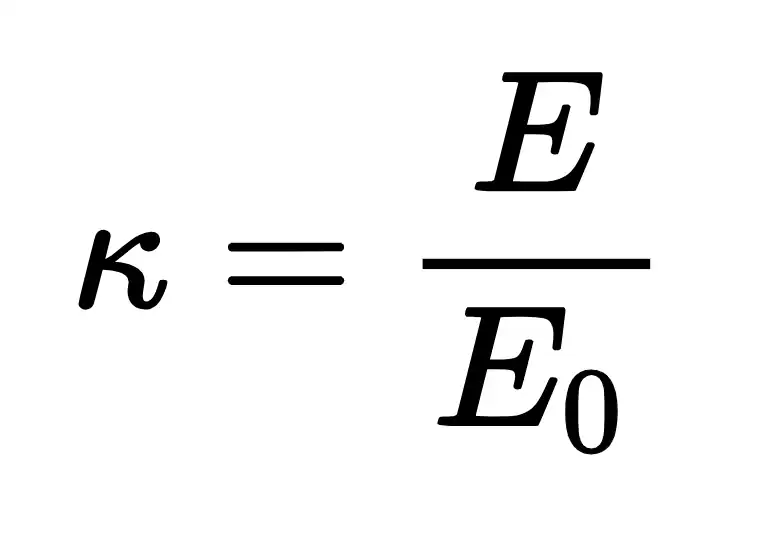
La permitividad relativa generalmente se denota como ε_r(ω), función de la permitividad absoluta respecto de la frecuencia, o como κ (kappa minúscula), valor constante, y se define de la siguiente manera:

ε ε r()⋅ ⋅ )=ε ε ()⋅ ⋅ )ε ε 0,{displaystyle varepsilon _{r}(omega)={frac {varepsilon (omega)}{varepsilon ♪♪

donde ε(ω) es la permitividad compleja dependiente de la frecuencia del material, y ε₀ es la permitividad del vacío.

Esto, se explica porque la permitividad (ε) es una propiedad física de los materiales que describe cómo se polarizan en presencia de un campo eléctrico. Un material con alta permitividad se polariza más fácilmente que uno con baja permitividad. Y dado que la permitividad del vacío (ε₀) es una constante universal que define la permitividad del espacio vacío, se puede abstraer un valor constante que represente su permitividad respecto de otros materiales.

La permitividad relativa es un número adimensional que en general tiene un valor complejo, sus partes real e imaginaria se denotan como:

ε ε r()⋅ ⋅ )=ε ε r.()⋅ ⋅ )− − iε ε r.()⋅ ⋅ ).{displaystyle varepsilon _{r}(omega)=varepsilon _{r}'(omega)-ivarepsilon _{r}''''(omega).}

La permitividad relativa de un medio está relacionada con su susceptibilidad eléctrica, χ_e, como ε_r(ω) = 1 + χ_e.

En medios anisotrópicos (como cristales no cúbicos), la permitividad relativa es un tensor de segundo rango.

Medición de la permitividad relativa

La permitividad estática relativa, ε_r, se puede medir para campos eléctricos estáticos de la siguiente manera: primero, la capacitancia de un capacitor de prueba, C₀, se mide con vacío entre sus placas. Luego, usando el mismo capacitor y distancia entre sus placas, se mide la capacitancia C con un dieléctrico entre las placas. La permitividad relativa se puede calcular entonces como

ε ε r=CC0.{displaystyle varepsilon ¿Qué? {C} {C_{0}}}

Para los campos electromagnéticos variables en el tiempo, esta cantidad se vuelve dependiente de la frecuencia. Una técnica indirecta para calcular ε_r es la conversión de resultados de medición de parámetros S de radiofrecuencia. En esta fuente bibliográfica se puede encontrar una descripción de las conversiones de parámetros S utilizadas con frecuencia para determinar el ε_r dependiente de la frecuencia. Alternativamente, pueden emplearse efectos basados en resonancia a frecuencias fijas.

Aplicaciones de la permitividad relativa

Energía

La permitividad relativa es una información esencial cuando se diseñan condensadores y en otras circunstancias en las que se espera que un material introduzca capacitancia en un circuito. Si un material con una permitividad relativa alta se coloca en un campo eléctrico, la magnitud de ese campo se reducirá considerablemente dentro del volumen del dieléctrico. Este hecho se usa comúnmente para aumentar la capacitancia de un diseño de capacitor en particular. Las capas debajo de los conductores grabados en las placas de circuito impreso (PCB) también actúan como dieléctricos.

• Diseño de condensadores: La permitividad relativa del material dieléctrico utilizado en un condensador determina su capacitancia.
• Cálculo del campo eléctrico: La permitividad relativa afecta la fuerza del campo eléctrico generado por una carga eléctrica en un material.
• Comportamiento de las ondas electromagnéticas: La permitividad relativa influye en la velocidad de propagación de las ondas electromagnéticas en un material.

Comunicación

Los dieléctricos se utilizan en las líneas de transmisión de radiofrecuencia (RF). En un cable coaxial, se puede usar polietileno entre el conductor central y el blindaje exterior. También se puede colocar dentro de guías de ondas para formar filtros. Las fibras ópticas son ejemplos de guías de ondas dieléctricas. Consisten en materiales dieléctricos dopados deliberadamente con impurezas para controlar el valor preciso de ε_r dentro de la sección transversal. Esto controla el índice de refracción del material y, por lo tanto, también los modos ópticos de transmisión. Sin embargo, en estos casos es técnicamente la permitividad relativa lo que importa, ya que no se operan en el límite electrostático.

Medio ambiente

La permitividad relativa del aire cambia con la temperatura, la humedad y la presión barométrica. Se pueden construir sensores para detectar cambios en la capacitancia causados por cambios en la permitividad relativa. La mayor parte de este cambio se debe a los efectos de la temperatura y la humedad, ya que la presión barométrica es bastante estable. Usando el cambio de capacitancia, junto con la temperatura medida, la humedad relativa se puede obtener usando fórmulas de ingeniería.

Química

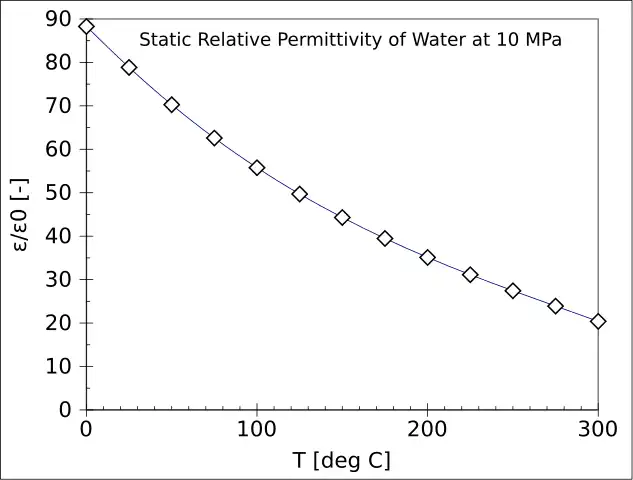
La permitividad estática relativa de un solvente es una medida relativa de su polaridad química. Por ejemplo, el agua es muy polar y tiene una permitividad estática relativa de 80,10 a 20 °C, mientras que el n-hexano no es polar y tiene una permitividad estática relativa de 1,89 a 20 °C. Esta información es importante al diseñar técnicas de separación, preparación de muestras y cromatografía en química analítica.

Sin embargo, la correlación debe tratarse con precaución. Por ejemplo, el diclorometano tiene un valor de ε_r de 9,08 (20 °C) y es poco soluble en agua (13 g/L o 9,8 mL/L a 20 °C); al mismo tiempo, el tetrahidrofurano tiene su ε_r = 7,52 a 22 °C, pero es completamente miscible con agua. En el caso del tetrahidrofurano, el átomo de oxígeno puede actuar como aceptor de enlaces de hidrógeno; mientras que el diclorometano no puede formar enlaces de hidrógeno con el agua.

Esto es aún más notable cuando se comparan los valores de ε_r del ácido acético (6,2528) y del yodoetano (7,6177). El gran valor numérico de ε_r no sorprende en el segundo caso, ya que el átomo de yodo es fácilmente polarizable; sin embargo, esto no implica que también sea polar (la polarizabilidad electrónica prevalece sobre la orientacional en este caso).

Permitividad relativa en medios con pérdida

Nuevamente, al igual que para la permitividad absoluta, la permitividad relativa para materiales con pérdida se puede formular como:

ε ε r=ε ε r.− − iσ σ ⋅ ⋅ ε ε 0,{displaystyle varepsilon _{r}=varepsilon ¿Por qué?

en términos de "conductividad dieléctrica" σ (unidades S/m, siemens por metro), que "suma todos los efectos disipativos del material; puede representar una conductividad [eléctrica] real causada por la migración de portadores de carga y también puede referirse a una pérdida de energía asociada con la dispersión de ε′ [la permitividad de valor real]" (pág. 8). Expandiendo la frecuencia angular ω = 2πc/λ y la constante eléctrica ε₀ = 1/ µ₀c², que se reduce a:

ε ε r=ε ε r.− − iσ σ λ λ κ κ ,{displaystyle varepsilon _{r}=varepsilon _{r}-isigma lambda kappa}

donde λ es la longitud de onda, c es la velocidad de la luz en el vacío y κ = µ₀c/2π = 59,95849 Ω ≈ 60,0 Ω es una constante recientemente introducida (unidades de ohmios, o siemens recíproco, tal que σλκ = ε_r permanece sin unidades).

Permitividad relativa en física

En la teoría causal de las ondas, la permitividad es una cantidad compleja. La parte imaginaria corresponde a un cambio de fase de la polarización P relativa a E y conduce a la atenuación de las ondas electromagnéticas que atraviesan el medio. Por definición, la permitividad relativa lineal del vacío es igual a 1, es decir, ε = ε₀, aunque existen efectos teóricos cuánticos no lineales en el vacío que se vuelven no despreciables a altas intensidades de campo.

La siguiente tabla proporciona algunos valores típicos.

Solvent		Permiso relativo	Temperatura
C6H6	benzene	2.3	298 K (25 °C)
Et2O	diethyl ether	4.3	293 K (20 °C)
(CH)2)4O	tetrahidrofuran (THF)	7.6	298 K (25 °C)
CH2Cl2	dichloromethane	9.1	293 K (20 °C)
NH3()liq)	amoníaco líquido	17	273 K (0 °C)
C2H5Oh.	etanol	24.3	298 K (25 °C)
CH3Oh.	metanol	32.7	298 K (25 °C)
CH3NO2	nitrometano	35,9	303 K (30 °C)
HCONMe2	dimetil formamide (DMF)	36,7	298 K (25 °C)
CH3CN	acetonitrile	37,5	293 K (20 °C)
H2O	agua	78.4	298 K (25 °C)
HCONH2	formamide	109	293 K (20 °C)

La permitividad relativa del hielo es ~3,15.

Permitividad relativa en metales

La permitividad generalmente se asocia con materiales dieléctricos, sin embargo, los metales se describen como que tienen una permitividad efectiva, con una permitividad relativa real igual a uno. En la región de baja frecuencia, que se extiende desde las radiofrecuencias hasta la región del infrarrojo lejano y los terahercios, la frecuencia de plasma del gas de electrones es mucho mayor que la frecuencia de propagación electromagnética, por lo que el índice de refracción n de un el metal es casi un número puramente imaginario. En el régimen de baja frecuencia, la permitividad relativa efectiva también es casi puramente imaginaria: tiene un valor imaginario muy grande relacionado con la conductividad y un valor real comparativamente insignificante.

Tabla de permitividad relativa (materiales comunes)

Material	Índice de Refracción
Vacío	1 (por definición)
Aire	1,000 589 86 ±0,000 000 50 (en STP, 900 kHz)
PTFE/Teflón	2,1
Polietileno/XLPE	2,25
Poliimida	3,4
Polipropileno	2,2 – 2,36
Poliestireno	2,4 – 2,7
Disulfuro de Carbono	2,6
BoPET	3,1
Papel (impresión)	1,4 (200 kHz)
Polímeros Electroactivos	2 – 12
Mica	3 – 6
Dióxido de Silicio	3,9
Zafiro	8,9 – 11,1 (anisotrópico)
Concreto	4,5
Pyrex (vidrio)	4,7 (3,7 – 10)
Neopreno	6,7
Caucho natural	7
Diamante	5,5 – 10
Sal	3 – 15
Resina de melamina	7,2 – 8,4
Grafito	10 – 15
Caucho de silicona	2,9 – 4
Silicio	11,68
GaAs	12,4
Nitruro de Silicio	7 – 8 (policristalino, 1 MHz)
Amoníaco	26, 22, 20, 17 (−80, −40, 0, +20 °C)
Metanol	30
Etilenglicol	37
Furfural	42,0
Glicerol	41,2, 47, 42,5 (0, 20, 25 °C)
Agua	87,9, 80,2, 55,5 (0, 20, 100 °C); 1,77 para luz visible
Ácido Fluorhídrico	175, 134, 111, 83,6 (−73, −42, −27, 0 °C)
Hidracina	52 (20 °C)
Formamida	84 (20 °C)
Ácido Sulfúrico	84 – 100 (20–25 °C)
Peróxido de Hidrógeno	128 acuoso – 60 (−30 – 25 °C)
Ácido Cíanhidrico	158,0 – 2,3 (0 – 21 °C)
Dióxido de Titanio	86 – 173
Titanato de Estroncio	310
Titanato de Bario Estroncio	500
Titanato de Bario	1200 – 10 000 (20–120 °C)
Titanato de Plomo y Circonio	500 – 6 000
Polímeros Conjugados	1,8 – 6 hasta 100 000
Titanato de Calcio y Cobre	>250 000