Permitividad
En electromagnetismo, la permitividad absoluta, a menudo llamada simplemente permitividad y denotada por la letra griega ε (epsilon), es una medida de la polarizabilidad eléctrica de un dieléctrico. Un material con alta permitividad se polariza más en respuesta a un campo eléctrico aplicado que un material con baja permitividad, por lo que almacena más energía en el material. En electrostática, la permitividad juega un papel importante en la determinación de la capacitancia de un capacitor.
En el caso más simple, el campo de desplazamiento eléctrico D resultante de un campo eléctrico aplicado E es
- D=ε ε E.{displaystyle mathbf {D} =varepsilon mathbf {E}
Más generalmente, la permitividad es una función termodinámica de estado. Puede depender de la frecuencia, magnitud y dirección del campo aplicado. La unidad SI para la permitividad es farad por metro (F/m).
La permitividad a menudo se representa mediante la permitividad relativa εr, que es la relación entre la permitividad absoluta ε y la permitividad de vacío ε0
- κ κ =ε ε r=ε ε ε ε 0{displaystyle kappa =varepsilon ¿Qué? }={frac {varepsilon }{varepsilon ♪♪.
Esta cantidad adimensional también se denomina a menudo y de forma ambigua como permitividad. Otro término común que se encuentra tanto para la permitividad absoluta como para la relativa es la constante dieléctrica, que ha quedado en desuso en la física y la ingeniería, así como en la química.
Por definición, un vacío perfecto tiene una permitividad relativa de exactamente 1, mientras que a temperatura y presión estándar, el aire tiene una permitividad relativa de κaire ≈ 1,0006.
La permitividad relativa está directamente relacionada con la susceptibilidad eléctrica (χ) por
- χ χ =κ κ − − 1{displaystyle chi =kappa -1}
de otro modo escrito como
- ε ε =ε ε rε ε 0=()1+χ χ )ε ε 0{displaystyle varepsilon =varepsilon ¿Qué? } 'varepsilon _{0}=(1+chi)varepsilon ¿Qué?
El término "permitividad" fue introducido en la década de 1880 por Oliver Heaviside para complementar la "permeabilidad" de Thomson (1872). Anteriormente escrito como p, la designación con ε ha sido de uso común desde la década de 1950.
Unidades
La unidad SI estándar para la permitividad es el farad por metro (F/m o F·m−1).
- Fm=CV⋅ ⋅ m=C2N⋅ ⋅ m2=C2⋅ ⋅ s2kg⋅ ⋅ m3=A2⋅ ⋅ s4kg⋅ ⋅ m3{displaystyle {frac {text{F}{text{m}}={frac {text{C}{text{V}}{cdot} {cdot}}} {cdot}} {cdot}}} {cdot}} {cdot}} {cdot}}}}}}} {ccdot}} {cdot}}}}}} {cdot}}}}} { {fnK} {f}} {fnK}} {f}} {f} {fn}} {cdot}} {cdot}} {cdot}}} {fn}} {fn}}}}} {cdot}} {cdot}} {f}}} {f} {f}}} {f}}}}}} {f}}}}} {f}} {f}}} {f}} {f}}}}} {f}}}}} {f}}}}}} {f}}} {f}}}}}}}}}}} {f} {f}} {f}}}}} {f}}}} {f} {f}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}} {fnK}} {fnMicroc} {fnMicrosoft Sans Serif} {cdot} {cdot}} {cdot}} {cdot}} {cdot}} {cdot}} {cdot}}} {cdot}} {cdot} {cdot}} {cdot} {cdot} {cdot} {cdot} {cdot} {cdot} {cdot} {cdot} {c} {cdot} {c} {cdot} {c} {c} {c} {c} {c} {c} {c} {c} {cdot} {c} {c} {cdot} {c} {cdot}}}}} {c} {cdot} {cdot} {c} {c} {c} {c} {c}}} {c {fnMicrosoft Sans} {fnMicrosoft} {cdot} {cdot} {fnK} {fnK}} {fnMicroc {f} {fnK}} {cdot} {cdot} {fnMicrosoft Sans} {fnMicrosoft} {cdot} {cdot} } {text{m}} {}}} {}}} {f}}} {f}}}}} {f}}}} {f}}}}}} {f}}}}}}} {f}}} {f}}}}} {f}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
Explicación
En electromagnetismo, el campo de desplazamiento eléctrico D representa la distribución de cargas eléctricas en un medio dado como resultado de la presencia de un campo eléctrico E. Esta distribución incluye la migración de carga y la reorientación del dipolo eléctrico. Su relación con la permitividad en el caso muy simple de materiales lineales, homogéneos, isotrópicos con valores "instantáneos" La respuesta a los cambios en el campo eléctrico es:
- D=ε ε E{displaystyle mathbf {D} =varepsilon mathbf {E}
donde la permitividad ε es un escalar. Si el medio es anisotrópico, la permitividad es un tensor de segundo rango.
En general, la permitividad no es una constante, ya que puede variar con la posición en el medio, la frecuencia del campo aplicado, la humedad, la temperatura y otros parámetros. En un medio no lineal, la permitividad puede depender de la fuerza del campo eléctrico. La permitividad en función de la frecuencia puede tomar valores reales o complejos.
En unidades SI, la permitividad se mide en faradios por metro (F/m o A2·s4·kg−1· m−3). El campo de desplazamiento D se mide en unidades de culombios por metro cuadrado (C/m2), mientras que el campo eléctrico E se mide en voltios por metro (V/m). D y E describen la interacción entre objetos cargados. D está relacionado con las densidades de carga asociadas con esta interacción, mientras que E está relacionado con las fuerzas y las diferencias de potencial.
Permisividad de vacío
La permitividad del vacío ε0 (también llamada permitividad del espacio libre o la constante eléctrica) es la relación D/E en forma gratuita espacio. También aparece en la constante de fuerza de Coulomb,
- ke=14π π ε ε 0{displaystyle k_{text{e}={frac} {1}{4pi varepsilon ♪♪
Su valor es
- ε ε 0=def1c02μ μ 0.. 8.8541878128()13)× × 10− − 12F/m{displaystyle varepsilon {fnMicrosoft} {fnMicrosoft}fnMicroc} {1}{0} {2}mu} _{0}}approx 8.854,8128(13)times 10^{-12}{text{text{ F/m }}
dónde
- c0 es la velocidad de la luz en el espacio libre,
- μ0 es la permeabilidad del vacío.
Las constantes c0 y μ0 ambos fueron definidos en unidades SI para tener valores numéricos exactos hasta la redefinición 2019 de las unidades base SI. Por lo tanto, hasta esa fecha, ε0 también se podría decir exactamente como una fracción, 1c02μ μ 0=135950207149.4727056π π F/m{fnMicroc} {1}{0} {2}mu} ¿Qué? {1}{35,950,207,149.472,7056pi }{text{ F/m}}incluso si el resultado era irracional (porque la fracción contenía) π). En contraste, el amperio fue una cantidad medida antes de 2019, pero desde entonces el amperio está ahora exactamente definido y es μ0 que es una cantidad de medida experimental (con la consiguiente incertidumbre) y por lo tanto es la nueva definición de 2019 ε0 ()c0 permanece exactamente definido antes y desde 2019).
Permisividad relativa
La permitividad lineal de un material homogéneo se suele dar en relación con la del espacio libre, como una permitividad relativa εr (también llamada constante dieléctrica, aunque este término está en desuso y, a veces, solo se refiere a la permitividad relativa estática de frecuencia cero). En un material anisotrópico, la permitividad relativa puede ser un tensor, causando birrefringencia. Luego, la permitividad real se calcula multiplicando la permitividad relativa por ε0:
- ε ε =ε ε rε ε 0=()1+χ χ )ε ε 0,{displaystyle varepsilon =varepsilon ¿Qué? } 'varepsilon _{0}=(1+chi)varepsilon ¿Qué?
donde χ (frecuentemente escrito χ e) es la susceptibilidad eléctrica del material.
La susceptibilidad se define como la constante de proporcionalidad (que puede ser un tensor) que relaciona un campo eléctrico E con la densidad de polarización dieléctrica inducida P tal que
- P=ε ε 0χ χ E,{displaystyle mathbf {P} = 'varepsilon ¿Por qué?
donde ε0 es la permitividad eléctrica del espacio libre.
La susceptibilidad de un medio está relacionada con su permitividad relativa εr por
- χ χ =ε ε r− − 1.{displaystyle chi =varepsilon _{mathrm {r} }-1.}
Entonces, en el caso de una aspiradora,
- χ χ =0.{displaystyle chi =0.}
La susceptibilidad también está relacionada con la polarizabilidad de las partículas individuales en el medio mediante la relación Clausius-Mossotti.
El desplazamiento eléctrico D está relacionado con la densidad de polarización P por
- D=ε ε 0E+P=ε ε 0()1+χ χ )E=ε ε rε ε 0E.{displaystyle mathbf {D} = 'varepsilon ♪♪Mathbf {E} +mathbf {P} =varepsilon _{0}(1+chi)mathbf {E} =varepsilon _{mathrm {r} } 'varepsilon Mathbf.
La permitividad ε y la permeabilidad µ de un medio juntos determinan la velocidad de fase v = c/n de radiación electromagnética a través de ese medio:
- ε ε μ μ =1v2.{displaystyle varepsilon mu ={frac {1}{v^{2}}}}
Aplicaciones prácticas
Determinación de la capacitancia
La capacitancia de un capacitor se basa en su diseño y arquitectura, lo que significa que no cambiará con la carga y descarga. La fórmula para la capacitancia en un capacitor de placas paralelas se escribe como
- C=ε ε Ad{displaystyle C=varepsilon {frac {} {}}}
Donde A{displaystyle A} es el área de un plato, d{displaystyle d} es la distancia entre las placas, y ε ε {displaystyle varepsilon } es el permiso del medio entre las dos placas. Para un condensador con permiso relativo κ κ {displaystyle kappa }, se puede decir que
- C=κ κ ε ε 0Ad{displaystyle C=kappa varepsilon - ¿Qué? {} {}}}
Ley de Gauss
La permitividad está relacionada con el flujo eléctrico (y, por extensión, con el campo eléctrico) a través de la ley de Gauss. La ley de Gauss establece que para una superficie gaussiana cerrada, S
- CCPR CCPR E=Qencε ε 0=∮ ∮ SE⋅ ⋅ dA{displaystyle Phi ¿Qué? Varepsilon ¿Qué? {}cdot mathrm {d} mathbf {A}
Donde CCPR CCPR E{displaystyle Phi _{E} es el flujo eléctrico neto que pasa por la superficie, Qenc{displaystyle Q_{text{enc}} es la carga encerrada en la superficie Gausiana, E{displaystyle mathbf {E} es el vector de campo eléctrico en un punto dado en la superficie, y dA{displaystyle mathrm {d} mathbf {A} es un vector de área diferencial en la superficie Gaussiana.
Si la superficie gaussiana encierra uniformemente una disposición de carga simétrica y aislada, la fórmula se puede simplificar a
- EA# ()Silencio Silencio )=Qencε ε 0{displaystyle EAcos(theta)={frac Varepsilon ♪♪
Donde Silencio Silencio {displaystyle theta } representa el ángulo entre las líneas de campo eléctrico y la normal (perpendicular) a S.
Si todas las líneas de campo eléctrico cruzan la superficie a 90°, la fórmula se puede simplificar aún más a
- E=Qencε ε 0A{displaystyle E={frac Varepsilon - Sí.
Porque la superficie de una esfera es 4π π r2{displaystyle 4pi r^{2}, el campo eléctrico a distancia r{displaystyle r} lejos de un arreglo de carga esférica uniforme
- E=Qε ε 0A=Qε ε 0()4π π r2)=Q4π π ε ε 0r2=kQr2{displaystyle E={frac {Q}{varepsilon ¿Qué? {Q}{varepsilon _{0}left(4pi r^{2}}={frac {Q}{4pi varepsilon ¿Qué?
Donde k{displaystyle k} es la constante de Coulomb (♪ ♪ 9.0× × 109m/F{displaystyle sim 9.0times 10^{9} {text{m}/{text{F}}). Esta fórmula se aplica al campo eléctrico debido a una carga de punto, fuera de una esfera de conducción o concha, fuera de una esfera aislante cargada uniformemente, o entre las placas de un condensador esférico.
Dispersión y causalidad
En general, un material no puede polarizarse instantáneamente en respuesta a un campo aplicado, por lo que la formulación más general en función del tiempo es
- P()t)=ε ε 0∫ ∫ − − JUEGO JUEGO tχ χ ()t− − t.)E()t.)dt..{displaystyle mathbf {P} (t)=varepsilon _{0}int _{-infty }^{t}chi left(t-t'right)mathbf {E} left(t'right),dt'.}
Es decir, la polarización es una convolución del campo eléctrico en tiempos anteriores con susceptibilidad dependiente del tiempo dada por χ(Δt). El límite superior de esta integral también se puede extender hasta el infinito si se define χ(Δt) = 0 para Δt < 0. Una respuesta instantánea correspondería a una susceptibilidad de función delta de Dirac χ(Δt) = χδ(Δt).
Es conveniente tomar la transformada de Fourier con respecto al tiempo y escribir esta relación en función de la frecuencia. Debido al teorema de convolución, la integral se convierte en un producto simple,
- P()⋅ ⋅ )=ε ε 0χ χ ()⋅ ⋅ )E()⋅ ⋅ ).{displaystyle mathbf {P} (omega)=varepsilon ¿Por qué? }
Esta dependencia de frecuencia de la susceptibilidad conduce a la dependencia de frecuencia de la permitividad. La forma de la susceptibilidad con respecto a la frecuencia caracteriza las propiedades de dispersión del material.
Además, el hecho de que la polarización solo puede depender del campo eléctrico en momentos anteriores (es decir, efectivamente χ(Δt) = 0 para Δt < 0), una consecuencia de la causalidad, impone restricciones de Kramers-Kronig sobre la susceptibilidad χ(0).
Permisividad compleja
A diferencia de la respuesta del vacío, la respuesta de los materiales normales a los campos externos generalmente depende de la frecuencia del campo. Esta dependencia de la frecuencia refleja el hecho de que la polarización de un material no cambia instantáneamente cuando se aplica un campo eléctrico. La respuesta siempre debe ser causal (que surja después del campo aplicado), que puede representarse mediante una diferencia de fase. Por esta razón, la permitividad a menudo se trata como una función compleja de la frecuencia (angular) ω del campo aplicado:
- ε ε → → ε ε ^ ^ ()⋅ ⋅ ){displaystyle varepsilon rightarrow {hat {varepsilon}}(omega)}
(ya que los números complejos permiten especificar la magnitud y la fase). Por lo tanto, la definición de permitividad se convierte en
- D0e− − i⋅ ⋅ t=ε ε ^ ^ ()⋅ ⋅ )E0e− − i⋅ ⋅ t,{displaystyle D_{0}e^{-iomega E_{0}e^{-iomega t}
dónde
- D0 y E0 son las amplitudes del desplazamiento y los campos eléctricos, respectivamente,
- i es la unidad imaginaria, i2 = 1 -.
La respuesta de un medio a campos eléctricos estáticos se describe mediante el límite de permitividad de baja frecuencia, también llamado permitividad estática εs (también εDC):
- ε ε s=lim⋅ ⋅ → → 0ε ε ^ ^ ()⋅ ⋅ ).{displaystyle varepsilon _{mathrm {s}=lim _{omega rightarrow 0}{hat {varepsilon }} {omega). }
En el límite de alta frecuencia (es decir, frecuencias ópticas), la permitividad compleja se conoce comúnmente como ε∞ (o a veces εopt). A la frecuencia del plasma y por debajo, los dieléctricos se comportan como metales ideales, con comportamiento de gas de electrones. La permitividad estática es una buena aproximación para campos alternos de bajas frecuencias y, a medida que la frecuencia aumenta, surge una diferencia de fase medible δ entre D y E. La frecuencia a la que el cambio de fase se vuelve perceptible depende de la temperatura y los detalles del medio. Para una intensidad de campo moderada (E0), D y E siguen siendo proporcionales, y
- ε ε ^ ^ =D0E0=Silencioε ε Silencioe− − iδ δ .{displaystyle {hat {varepsilon }={frac [D_{0} {E_{0}}= "Antes" Silencio. }
Dado que la respuesta de los materiales a campos alternos se caracteriza por una permitividad compleja, es natural separar sus partes real e imaginaria, lo cual se hace por convención de la siguiente manera:
- ε ε ^ ^ ()⋅ ⋅ )=ε ε .()⋅ ⋅ )− − iε ε .()⋅ ⋅ )=SilencioD0E0Silencio()# δ δ − − ipecado δ δ ).{displaystyle {hat {varepsilon } {omega)=varepsilon '(omega)-ivarepsilon '(omega)=left sometida{frac {D_{0} {E_{0}}}justo sobre la vidaleft(cos delta -isin delta right). }
dónde
- ε. es la parte real de la permittividad;
- ε. es la parte imaginaria de la permittividad;
- δ es el ángulo de pérdida.
La elección del signo para la dependencia del tiempo, e−iωt, dicta la convención de signos para la parte imaginaria de la permitividad. Los signos usados aquí corresponden a los comúnmente usados en física, mientras que para la convención de ingeniería se deben invertir todas las cantidades imaginarias.
La permitividad compleja suele ser una función complicada de la frecuencia ω, ya que es una descripción superpuesta de fenómenos de dispersión que ocurren en múltiples frecuencias La función dieléctrica ε(ω) debe tener polos solo para frecuencias con partes imaginarias positivas y, por lo tanto, satisface la Kramers– Relaciones de Kronig. Sin embargo, en los estrechos rangos de frecuencia que a menudo se estudian en la práctica, la permitividad se puede aproximar como independiente de la frecuencia o mediante funciones modelo.
A una frecuencia determinada, la parte imaginaria, ε″, conduce a una pérdida por absorción si es positiva (en la convención de signos anterior) y ganar si es negativo. De manera más general, se deben considerar las partes imaginarias de los valores propios del tensor dieléctrico anisotrópico.
En el caso de los sólidos, la función dieléctrica compleja está íntimamente relacionada con la estructura de bandas. La cantidad principal que caracteriza la estructura electrónica de cualquier material cristalino es la probabilidad de absorción de fotones, que está directamente relacionada con la parte imaginaria de la función dieléctrica óptica ε(ω). La función dieléctrica óptica viene dada por la expresión fundamental:
- ε ε ()⋅ ⋅ )=1+8π π 2e2m2.. c,v∫ ∫ Wc,v()E)()φ φ ()▪ ▪ ⋅ ⋅ − − E)− − φ φ ()▪ ▪ ⋅ ⋅ +E))dx.{displaystyle varepsilon (omega)=1+{frac {8pi ^{2}e^{2} {m^{2}}}sum _{c,v}int W_{c,v}(E){bigl (}varphi (hbar omega -E)-varphi (hbar omega +E){bigr)},dx.}
En esta expresión, Wc,v(E) representa el producto de la probabilidad de transición promediada por zona de Brillouin en la energía E con la densidad conjunta de estados, Jc,v( E); φ es una función de ampliación, que representa el papel de la dispersión en la dispersión de los niveles de energía. En general, el ensanchamiento es intermedio entre lorentziano y gaussiano; para una aleación, es algo más cercano a Gauss debido a la fuerte dispersión de las fluctuaciones estadísticas en la composición local en una escala nanométrica.
Permisividad tensorial
Según el modelo Drude de plasma magnetizado, una expresión más general que tiene en cuenta la interacción de los portadores con un campo eléctrico alterno a frecuencias milimétricas y de microondas en un semiconductor magnetizado axialmente requiere la expresión de la permitividad como un no- tensor diagonal. (ver también Electro-giración).
- D()⋅ ⋅ )=Silencioε ε 1− − iε ε 20iε ε 2ε ε 1000ε ε zSilencioE ()⋅ ⋅ ){displaystyle mathbf {D} (omega)={begin{vmatrix}varepsilon _{1} ¿Qué? ¿Qué? - ¿Qué? ¿Por qué?
Si ε2 desaparece, entonces el tensor es diagonal pero no proporcional a la identidad y se dice que el medio ser un medio uniaxial, que tiene propiedades similares a un cristal uniaxial.
Clasificación de materiales
| εr/εr | Conducción actual | propagación del terreno |
|---|---|---|
| 0 | perfecto medio sin pérdidas | |
| ≪ 1 | material de baja conductividad pobre conductor | medio de baja pérdida buena dieléctrica |
| Entendido 1 | material de ejecución | medio de propagación |
| ≫ 1 | material de alta conductividad buen conductor | medio alto pérdidas pobre dieléctrico |
| JUEGO | perfecto conductor |
Los materiales se pueden clasificar según su permitividad de valor complejo ε, al comparar su real ε′ y componentes imaginarios ε″ (o, equivalentemente, conductividad, σ, cuando se contabiliza en este último). Un conductor perfecto tiene una conductividad infinita, σ = ∞, mientras que un dieléctrico perfecto es un material que no tiene conductividad en absoluto, σ = 0; este último caso, de permitividad de valor real (o permitividad de valor complejo con componente imaginario cero) también se asocia con el nombre medios sin pérdidas. Generalmente, cuando σ/ωε′ ≪ 1 consideramos que el material es un dieléctrico de baja pérdida (aunque no exactamente sin pérdidas), mientras que σ/ωε′ ≫ 1 está asociado con un buen conductor; estos materiales con una conductividad no despreciable producen una gran cantidad de pérdidas que inhiben la propagación de las ondas electromagnéticas, por lo que también se dice que son medios con pérdidas. Se consideran medios generales aquellos materiales que no se encuentren dentro de ninguno de los dos límites.
Medio con pérdida
En el caso de un medio con pérdidas, es decir, cuando la corriente de conducción no es despreciable, la densidad de corriente total que fluye es:
- JTot=Jc+Jd=σ σ E+i⋅ ⋅ ε ε .E=i⋅ ⋅ ε ε ^ ^ E{displaystyle J_{text{tot}=J_{mathrm} {C}+J_{mathrm {d}=sigma E+iomega varepsilon 'E=iomega {hat {varepsilon }E}
dónde
- σ es la conductividad del medio;
- ε ε .=ε ε 0ε ε r{displaystyle varepsilon '=varepsilon _{0}varepsilon ¿Qué? es la parte real de la permitibilidad.
- ε ε ^ ^ =ε ε .− − iε ε .{displaystyle {hat {varepsilon }= 'varepsilon '-i 'varepsilon 'es el complejo permiso
Tenga en cuenta que esto está utilizando la convención de ingeniería eléctrica de la ambigüedad conjugada compleja; la convención de física/química involucra el complejo conjugado de estas ecuaciones.
El tamaño de la corriente de desplazamiento depende de la frecuencia ω del campo aplicado E; no hay corriente de desplazamiento en un campo constante.
En este formalismo, la permitividad compleja se define como:
- ε ε ^ ^ =ε ε .()1− − iσ σ ⋅ ⋅ ε ε .)=ε ε .− − iσ σ ⋅ ⋅ {displaystyle {hat {varepsilon }= 'varepsilon 'left(1-i{frac {sigma {omega varepsilon}right)=varepsilon '-i{frac {sigma }{omega }
En general, la absorción de energía electromagnética por parte de los dieléctricos está cubierta por algunos mecanismos diferentes que influyen en la forma de la permitividad en función de la frecuencia:
- Primero son los efectos de relajación asociados con dipoles moleculares permanentes e inducidos. En frecuencias bajas el campo cambia lentamente lo suficiente para permitir que los dipoles alcancen el equilibrio antes de que el campo haya cambiado mesurablemente. Para frecuencias en las que las orientaciones dipoles no pueden seguir el campo aplicado debido a la viscosidad del medio, la absorción de la energía del campo conduce a la disipación energética. El mecanismo de relajación de las dipoles se llama relajación dieléctrica y para dipoles ideales se describe por la relajación clásica de Debye.
- Segundo son los efectos de resonancia, que surgen de las rotaciones o vibraciones de átomos, iones o electrones. Estos procesos se observan en el barrio de sus frecuencias de absorción características.
Los efectos anteriores a menudo se combinan para causar efectos no lineales dentro de los capacitores. Por ejemplo, la absorción dieléctrica se refiere a la incapacidad de un capacitor que se ha cargado durante mucho tiempo para descargarse por completo cuando se descarga brevemente. Aunque un capacitor ideal permanecería en cero voltios después de descargarse, los capacitores reales desarrollarán un voltaje pequeño, un fenómeno que también se denomina remojo o acción de la batería. Para algunos dieléctricos, como muchas películas de polímero, el voltaje resultante puede ser inferior al 1 o 2 % del voltaje original. Sin embargo, puede llegar al 15-25 % en el caso de condensadores o supercondensadores electrolíticos.
Interpretación mecánico-cuántica
En términos de mecánica cuántica, la permitividad se explica por interacciones atómicas y moleculares.
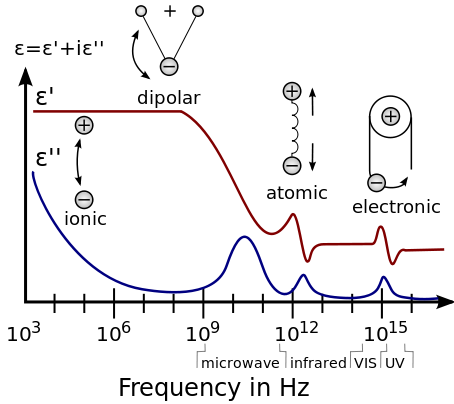
A bajas frecuencias, las moléculas en los dieléctricos polares se polarizan mediante un campo eléctrico aplicado, que induce rotaciones periódicas. Por ejemplo, a la frecuencia de microondas, el campo de microondas provoca la rotación periódica de las moléculas de agua, suficiente para romper los enlaces de hidrógeno. El campo realiza trabajo contra los enlaces y la energía es absorbida por el material en forma de calor. Esta es la razón por la que los hornos de microondas funcionan muy bien con materiales que contienen agua. Hay dos máximos del componente imaginario (el índice de absorción) del agua, uno en la frecuencia de microondas y el otro en la frecuencia ultravioleta lejana (UV). Ambas resonancias están a frecuencias más altas que la frecuencia operativa de los hornos de microondas.
A frecuencias moderadas, la energía es demasiado alta para provocar la rotación, pero demasiado baja para afectar directamente a los electrones, y se absorbe en forma de vibraciones moleculares resonantes. En el agua, aquí es donde el índice de absorción comienza a caer bruscamente, y el mínimo de la permitividad imaginaria está en la frecuencia de la luz azul (régimen óptico).
A altas frecuencias (como UV y superiores), las moléculas no pueden relajarse y la energía es absorbida puramente por los átomos, excitando los niveles de energía de los electrones. Por lo tanto, estas frecuencias se clasifican como radiación ionizante.
Si bien ahora es posible computacionalmente realizar un modelado ab initio completo (es decir, los primeros principios), aún no se ha aplicado ampliamente. Por lo tanto, se acepta un modelo fenomenológico como un método adecuado para capturar comportamientos experimentales. El modelo de Debye y el modelo de Lorentz utilizan una representación lineal de parámetros de sistema concentrados de primer y segundo orden (respectivamente) (como un circuito resonante RC y LRC).
Medición
La permitividad relativa de un material se puede encontrar mediante una variedad de mediciones eléctricas estáticas. La permitividad compleja se evalúa en una amplia gama de frecuencias mediante el uso de diferentes variantes de espectroscopia dieléctrica, cubriendo casi 21 órdenes de magnitud desde 10−6 hasta 1015 hercios. Además, mediante el uso de criostatos y hornos, las propiedades dieléctricas de un medio se pueden caracterizar en una variedad de temperaturas. Para estudiar sistemas para campos de excitación tan diversos, se utilizan varias configuraciones de medición, cada una adecuada para un rango de frecuencia especial.
Chen et al. describe varias técnicas de medición de microondas. Los errores típicos del método de Hakki-Coleman que emplea un disco de material entre planos conductores son de alrededor del 0,3 %.
- Mediciones de dominio de tiempo de baja frecuencia (10−6 a 103Hz)
- Mediciones de dominio de frecuencia baja (10); 5 - a 106Hz)
- Métodos coaxiales reflectantes (10)6 a 1010Hz)
- Método coaxial de transmisión (10)8 a 1011Hz)
- Métodos cuasi ópticos (109 a 1010Hz)
- Terahertz time-domain spectroscopy (1011 a 1013Hz)
- Métodos Fourier-transform (10)11 a 1015Hz)
En frecuencias infrarrojas y ópticas, una técnica común es la elipsometría. La interferometría de polarización dual también se usa para medir el índice de refracción complejo para películas muy delgadas en frecuencias ópticas.
Para la medición 3D de tensores dieléctricos a frecuencia óptica, se puede utilizar la tomografía de tensores dieléctricos [1].
Contenido relacionado
Teorema π de Buckingham
Gauss (unidad)
Electronvoltio