Orbitales moleculares

Conjunto orbital molecular de acetileno (H-Cristán-H). La columna izquierda muestra MO que están ocupados en el estado del suelo, con el orbital de menor energía en la parte superior. La línea blanca y gris visible en algunos MO's es el eje molecular que pasa por los núcleos. Las funciones de onda orbital son positivas en las regiones rojas y negativas en el azul. La columna derecha muestra el MO virtual que está vacío en el estado del suelo, pero puede estar ocupado en estados excitados.

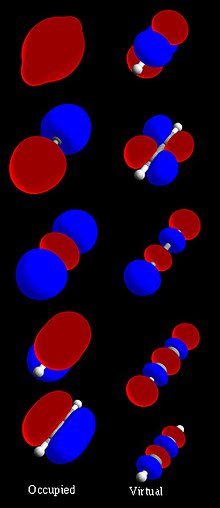
En química, un orbital molecular es una función matemática que describe la ubicación y el comportamiento ondulatorio de un electrón en una molécula. Esta función se puede utilizar para calcular propiedades químicas y físicas, como la probabilidad de encontrar un electrón en una región específica. Los términos orbital atómico y orbital molecular fueron introducidos por Robert S. Mulliken en 1932 para referirse a funciones de onda orbitales de un electrón. En un nivel elemental, se utilizan para describir la región del espacio en la que una función tiene una amplitud significativa.

En un átomo aislado, los electrones orbitales' la ubicación está determinada por funciones llamadas orbitales atómicos. Cuando múltiples átomos se combinan químicamente en una molécula, los electrones & # 39; las ubicaciones están determinadas por la molécula como un todo, por lo que los orbitales atómicos se combinan para formar orbitales moleculares. Los electrones de los átomos constituyentes ocupan los orbitales moleculares. Matemáticamente, los orbitales moleculares son una solución aproximada a la ecuación de Schrödinger para los electrones en el campo de los núcleos atómicos de la molécula. Por lo general, se construyen combinando orbitales atómicos u orbitales híbridos de cada átomo de la molécula, u otros orbitales moleculares de grupos de átomos. Se pueden calcular cuantitativamente utilizando los métodos de Hartree-Fock o de campo autoconsistente (SCF).

Los orbitales moleculares son de tres tipos: orbitales de enlace que tienen una energía inferior a la energía de los orbitales atómicos que los formaron y, por lo tanto, promueven los enlaces químicos que mantienen unida la molécula; orbitales antienlazantes que tienen una energía superior a la energía de sus orbitales atómicos constituyentes, y por tanto se oponen al enlace de la molécula, y orbitales no enlazantes que tienen la misma energía que sus orbitales atómicos constituyentes y, por lo tanto, no tienen ningún efecto sobre el enlace de la molécula.

Resumen

Se puede usar un orbital molecular (OM) para representar las regiones de una molécula donde es probable que se encuentre un electrón que ocupe ese orbital. Los orbitales moleculares son soluciones aproximadas de la ecuación de Schrödinger para los electrones en el campo eléctrico de los núcleos atómicos de las moléculas. Sin embargo, calcular los orbitales directamente a partir de esta ecuación es un problema demasiado intratable. En cambio, se obtienen de la combinación de orbitales atómicos, que predicen la ubicación de un electrón en un átomo. Un orbital molecular puede especificar la configuración electrónica de una molécula: la distribución espacial y la energía de uno (o un par de) electrones. Más comúnmente, un MO se representa como una combinación lineal de orbitales atómicos (el método LCAO-MO), especialmente en uso cualitativo o muy aproximado. Son invaluables para proporcionar un modelo simple de enlace en moléculas, entendido a través de la teoría de orbitales moleculares. La mayoría de los métodos actuales en química computacional comienzan calculando los OM del sistema. Un orbital molecular describe el comportamiento de un electrón en el campo eléctrico generado por los núcleos y alguna distribución promedio de los otros electrones. En el caso de dos electrones que ocupan el mismo orbital, el principio de Pauli exige que tengan espín opuesto. Necesariamente, esta es una aproximación, y las descripciones altamente precisas de la función de onda electrónica molecular no tienen orbitales (ver interacción de configuración).

Los orbitales moleculares están, en general, deslocalizados en toda la molécula. Además, si la molécula tiene elementos de simetría, sus orbitales moleculares no degenerados son simétricos o antisimétricos con respecto a cualquiera de estas simetrías. En otras palabras, la aplicación de una operación de simetría S (por ejemplo, una reflexión, rotación o inversión) al orbital molecular ψ da como resultado que el orbital molecular no cambie o invierta su signo matemático: S< /b>ψ = ±ψ. En moléculas planas, por ejemplo, los orbitales moleculares son simétricos (sigma) o antisimétricos (pi) con respecto a la reflexión en el plano molecular. Si también se consideran moléculas con energías orbitales degeneradas, se mantiene una afirmación más general de que los orbitales moleculares forman bases para las representaciones irreducibles del grupo de simetría de la molécula. Las propiedades de simetría de los orbitales moleculares significan que la deslocalización es una característica inherente de la teoría de orbitales moleculares y la hace fundamentalmente diferente (y complementaria) de la teoría del enlace de valencia, en la que los enlaces se ven como pares de electrones localizados, teniendo en cuenta la resonancia para explicar la deslocalización..

A diferencia de estos orbitales moleculares canónicos adaptados a la simetría, los orbitales moleculares localizados se pueden formar aplicando ciertas transformaciones matemáticas a los orbitales canónicos. La ventaja de este enfoque es que los orbitales se corresponderán más estrechamente con los "enlaces" de una molécula representada por una estructura de Lewis. Como desventaja, los niveles de energía de estos orbitales localizados ya no tienen significado físico. (La discusión en el resto de este artículo se centrará en los orbitales moleculares canónicos. Para obtener más información sobre los orbitales moleculares localizados, consulte: orbital de enlace natural y sigma-pi y modelos de orbitales equivalentes).

Formación de orbitales moleculares

Los orbitales moleculares surgen de las interacciones permitidas entre los orbitales atómicos, que están permitidas si las simetrías (determinadas a partir de la teoría de grupos) de los orbitales atómicos son compatibles entre sí. La eficiencia de las interacciones de los orbitales atómicos se determina a partir de la superposición (una medida de qué tan bien dos orbitales interactúan constructivamente entre sí) entre dos orbitales atómicos, lo cual es significativo si los orbitales atómicos tienen una energía similar. Finalmente, el número de orbitales moleculares formados debe ser igual al número de orbitales atómicos en los átomos que se combinan para formar la molécula.

Discusión cualitativa

Para una discusión imprecisa, pero cualitativamente útil, de la estructura molecular, los orbitales moleculares se pueden obtener del "Método de orbitales moleculares de combinación lineal de orbitales atómicos" Enfoque. Aquí, los orbitales moleculares se expresan como combinaciones lineales de orbitales atómicos.

Combinaciones lineales de orbitales atómicos (LCAO)

Los orbitales moleculares fueron introducidos por primera vez por Friedrich Hund y Robert S. Mulliken en 1927 y 1928. La combinación lineal de orbitales atómicos o "LCAO" La aproximación de orbitales moleculares fue introducida en 1929 por Sir John Lennard-Jones. Su innovador artículo mostró cómo derivar la estructura electrónica de las moléculas de flúor y oxígeno a partir de principios cuánticos. Este enfoque cualitativo de la teoría de orbitales moleculares es parte del comienzo de la química cuántica moderna. Las combinaciones lineales de orbitales atómicos (LCAO) se pueden utilizar para estimar los orbitales moleculares que se forman al unirse entre los átomos constituyentes de la molécula. Similar a un orbital atómico, una ecuación de Schrödinger, que describe el comportamiento de un electrón, también se puede construir para un orbital molecular. Las combinaciones lineales de orbitales atómicos, o las sumas y diferencias de las funciones de onda atómicas, proporcionan soluciones aproximadas a las ecuaciones de Hartree-Fock que corresponden a la aproximación de partículas independientes de la ecuación molecular de Schrödinger. Para moléculas diatómicas simples, las funciones de onda obtenidas se representan matemáticamente mediante las ecuaciones

${displaystyle Psi =c_{a}psi ¿Qué? ¿Qué?$

${displaystyle Psi ^{*}=c_{a}psi ¿Por qué? ¿Qué?$

Donde ${displaystyle Psi }$ y ${displaystyle Psi ^{*}$ son las funciones moleculares de onda para los orbitales moleculares de unión y antibón, respectivamente, ${displaystyle psi _{a}$ y ${displaystyle psi _{b}$ son las funciones de onda atómica de los átomos a y b, respectivamente, y ${displaystyle c_{a}$ y ${displaystyle C_{b}$ son coeficientes ajustables. Estos coeficientes pueden ser positivos o negativos, dependiendo de las energías y simetrías de las órbitas atómicas individuales. A medida que los dos átomos se acercan, sus órbitas atómicas se superponen para producir áreas de alta densidad de electrones y, como consecuencia, se forman órbitas moleculares entre los dos átomos. Los átomos se mantienen unidos por la atracción electrostática entre los núcleos cargados positivamente y los electrones cargados negativamente que ocupan órbitas moleculares de unión.

Mos enlazantes, antienlazantes y no enlazantes

Cuando los orbitales atómicos interactúan, el orbital molecular resultante puede ser de tres tipos: enlazante, antienlazante o no enlazante.

OM de vinculación:

• Las interacciones entre órbitas atómicas son interacciones constructivas (en fase).
• Bonificación Los MO son más bajos en energía que los orbitales atómicos que se combinan para producirlos.

OM antienlazantes:

• Las interacciones anticonceptivas entre órbitas atómicas son interacciones destructivas (fuera de fase), con un plano nodal donde la función de onda del orbital antibón es cero entre los dos átomos que interactúan
• Antibonding Los MO son más altos en energía que los orbitales atómicos que se combinan para producirlos.

Mos no enlazantes:

• Nonbonding Los MOs son el resultado de ninguna interacción entre órbitas atómicas debido a la falta de simetrías compatibles.
• Nonbonding MOs tendrá la misma energía que las órbitas atómicas de uno de los átomos en la molécula.

Etiquetas Sigma y pi para MO

El tipo de interacción entre orbitales atómicos se puede categorizar aún más mediante las etiquetas de simetría de orbitales moleculares σ (sigma), π (pi), δ (delta), φ (phi), γ (gamma), etc. Estos son los Letras griegas correspondientes a los orbitales atómicos s, p, d, f y g respectivamente. El número de planos nodales que contienen el eje internuclear entre los átomos en cuestión es cero para σ MO, uno para π, dos para δ, tres para φ y cuatro para γ.

Σ simetría

Un MO con simetría σ resulta de la interacción de dos orbitales atómicos s o dos orbitales atómicos p_z. Un MO tendrá simetría σ si el orbital es simétrico con respecto al eje que une los dos centros nucleares, el eje internuclear. Esto significa que la rotación del MO sobre el eje internuclear no da como resultado un cambio de fase. Un orbital σ*, un orbital antienlazante sigma, también mantiene la misma fase cuando gira alrededor del eje internuclear. El orbital σ* tiene un plano nodal que está entre los núcleos y es perpendicular al eje internuclear.

Π simetría

Un MO con simetría π resulta de la interacción de dos orbitales atómicos p_x o p_y. Un MO tendrá simetría π si el orbital es asimétrico con respecto a la rotación sobre el eje internuclear. Esto significa que la rotación del MO sobre el eje internuclear dará como resultado un cambio de fase. Hay un plano nodal que contiene el eje internuclear, si se consideran orbitales reales.

Un orbital π*, un orbital antienlazante pi, también producirá un cambio de fase cuando se gira alrededor del eje internuclear. El orbital π* también tiene un segundo plano nodal entre los núcleos.

Δ simetría

Un MO con simetría δ resulta de la interacción de dos átomos d_xy o d_{x²-y²orbitales. Debido a que estos orbitales moleculares involucran orbitales atómicos d de baja energía, se ven en complejos de metales de transición. Un orbital enlazante δ tiene dos planos nodales que contienen el eje internuclear, y un orbital antienlazante δ* también tiene un tercer plano nodal entre los núcleos.}

Φ simetría

Suitably alignment f atomic orbitals overlap to form phi molecular orbital (a phi bond)

Los químicos teóricos han conjeturado que son posibles los enlaces de orden superior, como los enlaces phi correspondientes a la superposición de orbitales atómicos f. No hay ningún ejemplo conocido de una molécula que pretenda contener un enlace phi.

Simetría de Gerade y Ungerade

Para las moléculas que poseen un centro de inversión (moléculas centrosimétricas), existen etiquetas adicionales de simetría que se pueden aplicar a los orbitales moleculares. Las moléculas centrosimétricas incluyen:

• Diatomía Homonuclear, X₂
• Octahedral, EX₆
• Plano cuadrado, EX₄.

Las moléculas no centrosimétricas incluyen:

• Diatomía heteronuclear, XY
• Tetraedral, EX₄.

Si la inversión a través del centro de simetría en una molécula da como resultado las mismas fases para el orbital molecular, entonces se dice que el MO tiene simetría gerade (g), de la palabra alemana par. Si la inversión a través del centro de simetría en una molécula resulta en un cambio de fase para el orbital molecular, entonces se dice que el MO tiene simetría ungerade (u), de la palabra alemana para impar. Para un MO enlazante con simetría σ, el orbital es σ_g (s' + s'' es simétrico), mientras que un MO antienlazante con simetría σ el orbital es σ_u, porque la inversión de s' – s'' es antisimétrico. Para un OM de enlace con simetría π, el orbital es π_u porque la inversión a través del centro de simetría produciría un cambio de signo (los dos orbitales atómicos p están en fase entre sí pero los dos lóbulos tienen signos opuestos), mientras que un MO antienlazante con simetría π es π_g porque la inversión a través del centro de simetría para no produciría un cambio de signo (los dos orbitales p son antisimétricos por fase).

Diagramas MO

El enfoque cualitativo del análisis MO utiliza un diagrama de orbitales moleculares para visualizar las interacciones de enlace en una molécula. En este tipo de diagrama, los orbitales moleculares están representados por líneas horizontales; cuanto más alta es una línea, mayor es la energía del orbital, y los orbitales degenerados se colocan en el mismo nivel con un espacio entre ellos. Luego, los electrones a colocar en los orbitales moleculares se colocan uno por uno, teniendo en cuenta el principio de exclusión de Pauli y la regla de Hund de máxima multiplicidad (solo 2 electrones, con espines opuestos, por orbital; coloque tantos electrones desapareados en un nivel de energía como sea posible antes de comenzar a emparejarlos). Para moléculas más complicadas, el enfoque de la mecánica ondulatoria pierde utilidad en la comprensión cualitativa del enlace (aunque sigue siendo necesario para un enfoque cuantitativo). Algunas propiedades:

• Un conjunto de bases de órbitas incluye las órbitas atómicas disponibles para las interacciones orbitales moleculares, que pueden estar vinculadas o antibonando
• El número de órbitas moleculares es igual al número de órbitas atómicas incluidas en la expansión lineal o en el conjunto de bases
• Si la molécula tiene alguna simetría, las órbitas atómicas degeneradas (con la misma energía atómica) se agrupan en combinaciones lineales (llamadas orbitales atómicos adaptados a la simetría (SO)), que pertenecen a la representación del grupo de simetría, por lo que las funciones de onda que describen el grupo son conocidas como symmetry-adapted linear combinations ()SALC).
• El número de orbitales moleculares pertenecientes a una representación grupal es igual al número de órbitas atómicas adaptadas a la simetría pertenecientes a esta representación
• Dentro de una representación particular, las órbitas atómicas adaptadas a la simetría se mezclan más si sus niveles de energía atómica están más cerca.

El procedimiento general para construir un diagrama de orbitales moleculares para una molécula razonablemente simple se puede resumir de la siguiente manera:

1. Asigne un grupo de puntos a la molécula.

2. Busque las formas de los SALC.

3. Organice los SALC de cada fragmento molecular en orden creciente de energía, observando primero si provienen de los orbitales s, p o d (y ponerlos en el orden s < p < d), y luego su número de nodos internucleares.

4. Combine SALC del mismo tipo de simetría de los dos fragmentos, y de N SALC forme N orbitales moleculares.

5. Estime las energías relativas de los orbitales moleculares a partir de consideraciones de superposición y energías relativas de los orbitales principales, y dibuje los niveles en un diagrama de niveles de energía de orbitales moleculares (que muestre el origen de los orbitales).

6. Confirme, corrija y revise este orden cualitativo realizando un cálculo de orbitales moleculares utilizando un software comercial.

Enlace en orbitales moleculares

Degeneración orbital

Se dice que los orbitales moleculares están degenerados si tienen la misma energía. Por ejemplo, en las moléculas diatómicas homonucleares de los primeros diez elementos, los orbitales moleculares derivados de los orbitales atómicos p_x y p_y dan como resultado dos orbitales de enlace degenerados (de baja energía) y dos orbitales antienlazantes degenerados (de alta energía).

Enlaces iónicos

Cuando la diferencia de energía entre los orbitales atómicos de dos átomos es bastante grande, los orbitales de un átomo contribuyen casi por completo a los orbitales de enlace y los orbitales del otro átomo contribuyen casi por completo a los orbitales de antienlace. Así, la situación es efectivamente que uno o más electrones han sido transferidos de un átomo al otro. Esto se llama un enlace (principalmente) iónico.

Orden de bonos

El orden de enlace, o el número de enlaces, de una molécula se puede determinar combinando el número de electrones en los orbitales moleculares enlazantes y antienlazantes. Un par de electrones en un orbital enlazante crea un enlace, mientras que un par de electrones en un orbital antienlazante niega un enlace. Por ejemplo, N₂, con ocho electrones en orbitales enlazantes y dos electrones en orbitales antienlazantes, tiene un orden de enlace de tres, lo que constituye un enlace triple.

La fuerza de la unión es proporcional al orden de la unión: una mayor cantidad de unión produce una unión más estable y la longitud de la unión es inversamente proporcional: una unión más fuerte es más corta.

Existen raras excepciones al requisito de que la molécula tenga un orden de enlace positivo. Aunque Be₂ tiene un orden de enlace de 0 según el análisis de MO, existe evidencia experimental de una molécula de Be₂ altamente inestable que tiene una longitud de enlace de 245 pm y una energía de enlace de 10 kJ/mol.

HOMO y LUMO

El orbital molecular ocupado más alto y el orbital molecular desocupado más bajo a menudo se denominan HOMO y LUMO, respectivamente. La diferencia de las energías de HOMO y LUMO se denomina brecha HOMO-LUMO. Esta noción es a menudo motivo de confusión en la literatura y debe considerarse con cautela. Su valor suele estar situado entre el gap fundamental (diferencia entre el potencial de ionización y la afinidad electrónica) y el gap óptico. Además, la brecha HOMO-LUMO se puede relacionar con una brecha de banda de material a granel o una brecha de transporte, que suele ser mucho más pequeña que la brecha fundamental.

Ejemplos

Diatómicas homonucleares

Los OM diatómicos homonucleares contienen contribuciones iguales de cada orbital atómico en el conjunto base. Esto se muestra en los diagramas MO diatómicos homonucleares para H₂, He₂ y Li₂, todos los cuales contienen orbitales simétricos.

H2

Funciones de onda de electrones para los 1s orbitales de un átomo de hidrógeno solitario (izquierda y derecha) y la unión correspondiente (abajo) y orbitales moleculares antibón (top) de la H₂ molécula. La parte real de la función de onda es la curva azul, y la parte imaginaria es la curva roja. Los puntos rojos marcan las ubicaciones de los núcleos. La función de onda electron oscila según la ecuación de onda Schrödinger, y los orbitales son sus ondas de pie. La frecuencia de onda de pie es proporcional a la energía cinética de la órbita. (Esta trama es una rebanada unidimensional a través del sistema tridimensional.)

Como ejemplo simple de MO, considere los electrones en una molécula de hidrógeno, H₂ (vea el diagrama de orbitales moleculares), con los dos átomos etiquetados como H' y H". Los orbitales atómicos de menor energía, 1s' y 1s", no se transforman según las simetrías de la molécula. Sin embargo, los siguientes orbitales atómicos adaptados a la simetría sí lo hacen:

La combinación simétrica (llamada orbital enlazante) tiene una energía más baja que los orbitales base, y la combinación antisimétrica (llamada orbital antienlazante) es más alta. Debido a que la molécula de H₂ tiene dos electrones, ambos pueden ir en el orbital de enlace, lo que hace que el sistema tenga menos energía (por lo tanto, más estable) que dos átomos de hidrógeno libres. Esto se llama enlace covalente. El orden de enlace es igual al número de electrones enlazantes menos el número de electrones antienlazantes, dividido por 2. En este ejemplo, hay 2 electrones en el orbital enlazante y ninguno en el orbital antienlazante; el orden de enlace es 1 y hay un enlace simple entre los dos átomos de hidrógeno.

Él2

Por otro lado, considere la molécula hipotética de He₂ con los átomos etiquetados como He' y El'. Al igual que con H₂, los orbitales atómicos de menor energía son los 1s' y 1s", y no se transforman según las simetrías de la molécula, mientras que los orbitales atómicos adaptados a la simetría sí lo hacen. La combinación simétrica, el orbital enlazante, tiene una energía más baja que los orbitales base, y la combinación antisimétrica, el orbital antienlazante, es más alta. A diferencia del H₂, con dos electrones de valencia, el He₂ tiene cuatro en su estado fundamental neutro. Dos electrones llenan el orbital de enlace de menor energía, σ_g(1s), mientras que los dos restantes llenan el orbital de antienlace de mayor energía, σ_u*(1s). Por lo tanto, la densidad de electrones resultante alrededor de la molécula no favorece la formación de un enlace entre los dos átomos; sin un enlace estable que mantenga unidos a los átomos, no se esperaría que la molécula existiera. Otra forma de verlo es que hay dos electrones enlazantes y dos electrones antienlazantes; por lo tanto, el orden de enlace es 0 y no existe ningún enlace (la molécula tiene un estado de enlace respaldado por el potencial de Van der Waals).

Li2

El dilitio Li₂ se forma a partir de la superposición de los orbitales atómicos 1s y 2s (el conjunto base) de dos átomos de Li. Cada átomo de Li aporta tres electrones para las interacciones de enlace, y los seis electrones llenan los tres OM de menor energía, σ_g(1s), σ_u*(1s) y σ_g(2s). Usando la ecuación para el orden de enlace, se encuentra que el dilitio tiene un orden de enlace de uno, un enlace simple.

Gases nobles

Considerando una molécula hipotética de He₂, dado que el conjunto básico de orbitales atómicos es el mismo que en el caso de H₂, encontramos que tanto el enlace como los orbitales de antienlace están llenos, por lo que no hay ventaja energética para el par. HeH tendría una ligera ventaja energética, pero no tanto como H₂ + 2 He, por lo que la molécula es muy inestable y existe solo brevemente antes de descomponerse en hidrógeno y helio. En general, encontramos que los átomos como el He que tienen capas de energía completa rara vez se unen con otros átomos. A excepción de los complejos de Van der Waals de vida corta, se conocen muy pocos compuestos de gases nobles.

Diatómicas heteronucleares

Mientras que los MO para moléculas diatómicas homonucleares contienen contribuciones iguales de cada orbital atómico que interactúa, los MO para diatómicos heteronucleares contienen diferentes contribuciones de orbitales atómicos. Las interacciones orbitales para producir orbitales enlazantes o antienlazantes en diatómicas heteronucleares ocurren si hay suficiente superposición entre los orbitales atómicos según lo determinado por sus simetrías y similitudes en las energías orbitales.

HF

En el fluoruro de hidrógeno, la simetría permite la superposición de HF entre los orbitales H 1s y F 2s, pero la diferencia de energía entre los dos orbitales atómicos evita que interactúen para crear un orbital molecular. La superposición entre los orbitales H 1s y F 2p_z también es simétricamente permitida, y estos dos orbitales atómicos tienen una pequeña separación de energía. Por lo tanto, interactúan, lo que conduce a la creación de OM σ y σ* y una molécula con un orden de enlace de 1. Dado que HF es una molécula no centrosimétrica, las etiquetas de simetría g y u no se aplican a sus orbitales moleculares.

Enfoque cuantitativo

Para obtener valores cuantitativos para los niveles de energía molecular, es necesario tener orbitales moleculares que sean tales que la expansión de la interacción de configuración (CI) converja rápidamente hacia el límite total de CI. El método más común para obtener dichas funciones es el método de Hartree-Fock, que expresa los orbitales moleculares como funciones propias del operador de Fock. Por lo general, se resuelve este problema expandiendo los orbitales moleculares como combinaciones lineales de funciones gaussianas centradas en los núcleos atómicos (ver combinación lineal de orbitales atómicos y conjunto de bases (química)). La ecuación para los coeficientes de estas combinaciones lineales es una ecuación de valores propios generalizada conocida como ecuaciones de Roothaan, que de hecho son una representación particular de la ecuación de Hartree-Fock. Hay una serie de programas en los que se pueden realizar cálculos químicos cuánticos de MO, incluido Spartan.

Relaciones simples a menudo sugieren que las energías orbitales moleculares experimentales se pueden obtener mediante métodos de espectroscopia de fotoelectrones ultravioleta para orbitales de valencia y espectroscopia de fotoelectrones de rayos X para orbitales centrales. Esto, sin embargo, es incorrecto ya que estos experimentos miden la energía de ionización, la diferencia de energía entre la molécula y uno de los iones resultante de la eliminación de un electrón. Las energías de ionización están vinculadas aproximadamente a las energías orbitales por Koopmans' teorema. Si bien la concordancia entre estos dos valores puede ser cercana para algunas moléculas, puede ser muy pobre en otros casos.