Número de reproducción básico

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Métrica en epidemiología

En la epidemiología, la Número básico de reproduccióno Número básico de reproducción (A veces se llama ratio de reproducción básica o Tasa reproductiva básica), denotado ${displaystyle R_{0}}$ (pronunciado No. o R 0), de una infección es el número esperado de casos directamente generados por un caso en una población donde todas las personas son susceptibles a la infección. La definición supone que ningún otro individuo está infectado o inmunizado (natural o mediante la vacunación). Algunas definiciones, como la del Departamento de Salud de Australia, añaden la ausencia de "toda intervención deliberada en la transmisión de enfermedades". El número de reproducción básica no es necesariamente el mismo que el número de reproducción efectiva ${displaystyle R}$ (usualmente escrito ${displaystyle R_{t}}$ [t por tiempo], a veces ${displaystyle R_{e}}$ ), que es el número de casos generados en el estado actual de una población, que no tiene que ser el estado no infectado. ${displaystyle R_{0}}$ es un número sin dimensiones (personas infectadas por persona infectando) y no una tasa de tiempo, que tendría unidades de tiempo⁻¹, o unidades de tiempo como duplicar el tiempo.

${displaystyle R_{0}}$ no es una constante biológica para un patógeno ya que también se ve afectada por otros factores como las condiciones ambientales y el comportamiento de la población infectada. ${displaystyle R_{0}}$ los valores generalmente se calculan a partir de modelos matemáticos, y los valores estimados dependen del modelo utilizado y los valores de otros parámetros. Así, los valores dados en la literatura sólo tienen sentido en el contexto dado y no se recomienda comparar valores basados en diferentes modelos. ${displaystyle R_{0}}$ no da por sí mismo una estimación de lo rápido que se propaga una infección en la población.

Los usos más importantes ${displaystyle R_{0}}$ están determinando si una enfermedad infecciosa emergente puede propagarse en una población y determinar qué proporción de la población debe inmunizarse mediante la vacunación para erradicar una enfermedad. En modelos de infección comúnmente usados, cuando $1}" xmlns="http://www.w3.org/1998/Math/MathML">R0■1{displaystyle R_{0} confía1}1}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert skin-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4fe3d7b35bd213a0e444b6f87fe6f4ce69ac0412" style="vertical-align: -0.671ex; width:7.079ex; height:2.509ex;"/>$ la infección será capaz de empezar a diseminarse en una población, pero no si $<math alttext="{displaystyle R_{0}R0c)1{displaystyle R_{0}traducido1}<img alt="{displaystyle R_{0}$ . En general, cuanto mayor sea el valor ${displaystyle R_{0}}$ , lo más difícil es controlar la epidemia. Para los modelos simples, la proporción de la población que necesita ser inmunizada eficazmente (que significa que no es susceptible a la infección) para prevenir la propagación sostenida de la infección debe ser mayor que ${displaystyle 1-1/R_{0}}$ . Este es el llamado Inmunidad umbral o nivel de inmunidad. Aquí, la inmunidad de rebaño significa que la enfermedad no puede propagarse en la población porque cada persona infectada, en promedio, sólo puede transmitir la infección a menos de otro contacto. Por el contrario, la proporción de la población que sigue siendo susceptible a la infección en el equilibrio endémico es ${displaystyle 1/R_{0}}$ . Sin embargo, este umbral se basa en modelos simples que asumen una población totalmente mixta sin relaciones estructuradas entre los individuos. Por ejemplo, si hay alguna correlación entre la inmunización de las personas (por ejemplo, vacunación) estado, entonces la fórmula ${displaystyle 1-1/R_{0}}$ puede subestimar el umbral de inmunidad de rebaño.

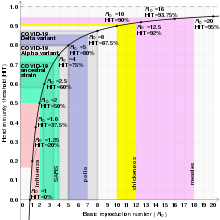
El número de reproducción básico se ve afectado por varios factores, incluida la duración de la infectividad de las personas afectadas, la contagiosidad del microorganismo y la cantidad de personas susceptibles en la población con las que entran en contacto las personas infectadas.

Historia

Las raíces del concepto de reproducción básica se pueden rastrear a través de la obra de Ronald Ross, Alfred Lotka y otros, pero su primera aplicación moderna en epidemiología fue por George Macdonald en 1952, quien construyó modelos de población de la propagación de la malaria. En su trabajo llamó la tasa de reproducción básica de la cantidad y la denotó por ${displaystyle Z_{0}}$ .

Panorama general de los métodos de estimación R0

Modelos compartimentales

Los modelos compartimentales son una técnica de modelado general a menudo aplicada al modelado matemático de enfermedades infecciosas. En estos modelos, los miembros de la población están asignados a 'compartamentos' con etiquetas, por ejemplo, S, I, o R, (Susceptible, Infeccioso o Recuperado). Estos modelos se pueden utilizar para estimar ${displaystyle R_{0}}$ .

Modelos de epidemia en redes

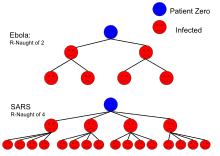
Las epidemias pueden modelarse como enfermedades que se propagan a través de redes de contacto y transmisión de enfermedades entre personas. Los nodos en estas redes representan individuos y los enlaces (bordes) entre nodos representan el contacto o la transmisión de enfermedades entre ellos. Si dicha red es una red local en forma de árbol, entonces la reproducción básica se puede escribir en términos del grado excesivo promedio de la red de transmisión de manera que:

{displaystyle R_{0}={frac {langle k^{2}rangle }{langle krangle }}-1,}

Donde ${displaystyle {langle krangle }}$ es el grado medio de la red y ${displaystyle {langle k^{2}rangle }}$ es el segundo momento de la distribución del grado de red de transmisión.

Poblaciones heterogéneas

En poblaciones que no son homogéneas, la definición de ${displaystyle R_{0}}$ es más sutil. La definición debe explicar el hecho de que un individuo infectado típico puede no ser un individuo promedio. Como ejemplo extremo, considere una población en la que una pequeña parte de los individuos se mezclan completamente entre sí mientras que los individuos restantes están aislados. Una enfermedad puede ser capaz de diseminarse en la porción totalmente mezclada, aunque un individuo seleccionado aleatoriamente conduciría a menos de un caso secundario. Esto se debe a que el individuo infectado típico está en la porción totalmente mezclada y por lo tanto es capaz de causar infecciones con éxito. En general, si las personas infectadas tempranamente en una epidemia son en promedio más probable o menos probable que transmitan la infección que las personas infectadas tardíamente en la epidemia, entonces la computación de ${displaystyle R_{0}}$ debe tener en cuenta esta diferencia. Una definición apropiada ${displaystyle R_{0}}$ en este caso es "el número esperado de casos secundarios producidos, en una población completamente susceptible, producidos por un individuo infectado típico".

El número básico de reproducción se puede calcular como una relación de tasas conocidas con el tiempo: si un contacto individual contagioso ${displaystyle beta }$ otras personas por unidad de tiempo, si todas esas personas se supone que contraen la enfermedad, y si la enfermedad tiene un período infeccioso promedio ${displaystyle {dfrac {1}{gamma }}}$ , entonces el número de reproducción básica es sólo ${displaystyle R_{0}={dfrac {beta }{gamma }}}$ . Algunas enfermedades tienen múltiples períodos de latencia posibles, en cuyo caso el número de reproducción para la enfermedad en general es la suma del número de reproducción para cada tiempo de transición en la enfermedad.

Número de reproducción efectiva

Una explicación de la

{displaystyle R}

Número en términos simples del Gobierno de Gales.

En realidad, las proporciones variables de la población son inmunes a cualquier enfermedad dada en cualquier momento. Para explicar esto, el número de reproducción eficaz ${displaystyle R_{e}}$ o ${displaystyle R}$ se utiliza. ${displaystyle R_{t}}$ es el número promedio de nuevas infecciones causadas por un solo individuo infectado a la vez t en la población parcialmente susceptible. Se puede encontrar multiplicando ${displaystyle R_{0}}$ por la fracción S de la población susceptible. Cuando la fracción de la población que es inmune aumenta (es decir, la población susceptible S disminuciones) tanto que ${displaystyle R_{e}}$ gots below, herd impunity has been achieved and the number of cases occurring in the population will gradually decrease to cero.

Limitaciones de R0

Utilización ${displaystyle R_{0}}$ en la prensa popular ha llevado a malentendidos y distorsiones de su significado. ${displaystyle R_{0}}$ se puede calcular a partir de muchos modelos matemáticos diferentes. Cada uno de estos puede dar una estimación diferente ${displaystyle R_{0}}$ , que debe ser interpretado en el contexto de ese modelo. Por lo tanto, el contagio de diferentes agentes infecciosos no se puede comparar sin recalcular ${displaystyle R_{0}}$ con suposiciones invariantes. ${displaystyle R_{0}}$ los valores de los brotes anteriores podrían no ser válidos para los brotes actuales de la misma enfermedad. En términos generales, ${displaystyle R_{0}}$ se puede utilizar como un umbral, incluso si se calcula con diferentes métodos: si $<math alttext="{displaystyle R_{0}R0c)1{displaystyle R_{0}traducido1}<img alt="{displaystyle R_{0}$ , el brote morirá, y si $1}" xmlns="http://www.w3.org/1998/Math/MathML">R0■1{displaystyle R_{0} confía1}1}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert skin-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4fe3d7b35bd213a0e444b6f87fe6f4ce69ac0412" style="vertical-align: -0.671ex; width:7.079ex; height:2.509ex;"/>$ , el brote se expandirá. En algunos casos, para algunos modelos, valores $<math alttext="{displaystyle R_{0}R0c)1{displaystyle R_{0}traducido1}<img alt="{displaystyle R_{0}$ todavía puede conducir a brotes autoperpetuantes. Esto es particularmente problemático si hay vectores intermedios entre los anfitriones (como ocurre con los zoonosis), como la malaria. Por lo tanto, comparaciones entre valores de los "Valores de ${displaystyle R_{0}}$ de las enfermedades contagiosas bien conocidas" mesa debe ser con precaución.

Aunque ${displaystyle R_{0}}$ no se puede modificar mediante la vacunación u otros cambios en la susceptibilidad de la población, puede variar según una serie de factores biológicos, sociobehavioales y ambientales. También puede ser modificado por el distanciamiento físico y otras políticas públicas o intervenciones sociales, aunque algunas definiciones históricas excluyen cualquier intervención deliberada en la reducción de la transmisión de enfermedades, incluyendo intervenciones no farmacológicas. Y de hecho, si las intervenciones no farmacológicas se incluyen en ${displaystyle R_{0}}$ A menudo depende del papel, la enfermedad y qué pasa si se está estudiando alguna intervención. Esto crea cierta confusión, porque ${displaystyle R_{0}}$ no es una constante; mientras que la mayoría de los parámetros matemáticos con subscriptos "no comprados" son constantes.

${displaystyle R}$ depende de muchos factores, muchos de los cuales necesitan ser estimados. Cada uno de estos factores añade a la incertidumbre en las estimaciones de ${displaystyle R}$ . Many of these factors are not important for informing public policy. Por lo tanto, la política pública puede ser mejor aplicada por métricas similares a las ${displaystyle R}$ , pero que son más sencillos de estimar, como duplicar el tiempo o la vida media ( ${displaystyle t_{1/2}}$ ).

Métodos utilizados para calcular ${displaystyle R_{0}}$ incluyen la función de supervivencia, reorganizando el mayor valor eigenvalo de la matriz Jacobiana, el método de próxima generación, cálculos de la tasa de crecimiento intrínseco, existencia del equilibrio endémico, el número de susceptibles en el equilibrio endémico, la edad promedio de infección y la ecuación de tamaño final. Pocos de estos métodos coinciden entre sí, incluso cuando comienzan con el mismo sistema de ecuaciones diferenciales. Incluso menos calculan el promedio de infecciones secundarias. Desde ${displaystyle R_{0}}$ rara vez se observa en el campo y se calcula generalmente a través de un modelo matemático, esto limita severamente su utilidad.

Valores de muestra para diversas enfermedades contagiosas

A pesar de las dificultades de estimación ${displaystyle R_{0}}$ mencionado en la sección anterior, se han hecho estimaciones para varios géneros, y se muestran en esta tabla. Cada género puede estar compuesto de muchas especies, cepas o variantes. Estimaciones de ${displaystyle R_{0}}$ para las especies, las cepas y las variantes son generalmente menos precisas que para los géneros, y también se proporcionan en tablas separadas a continuación para enfermedades de interés particular (influenza y COVID-19).

Valores de R₀ y umbrales de inmunidad (HIT) de enfermedades contagiosas antes de la intervención
Enfermedad	Transmisión	R₀	HIT
Sarampión	Aerosol	12 a 18	92-94%
Chickenpox (varicella)	Aerosol	10 a 12	90-92%
Mamadas	Caídas respiratorias	10 a 12	90-92%
COVID-19 (ver valores para cepas específicas a continuación)	Caídas respiratorias y aerosol	2.9-9.5	65 a 89%
Rubella	Caídas respiratorias	6 a 7	83-86%
Polio	Ruta fecal-oral	5 a 7	80-86%
Pertussis	Caídas respiratorias	5,5	82%
Pequeña viruela	Caídas respiratorias	3.5-6.0	71-83%
VIH/SIDA	Fluidos corporales	2 a 5	50-80%
SARS	Caídas respiratorias	2 a 4	50-75%
Diphtheria	Saliva	2.6 ()1.7–4.3)	62% ()41–77%)
Frío común (por ejemplo, rinovirus)	Caídas respiratorias	2 a 3	50 a 67%
Mpox	Contacto físico, fluidos corporales, gotitas respiratorias, sexual (MSM)	2.1 ()1.1–2.7)	53% ()22–63%)
Ebola (2014 brote)	Fluidos corporales	1.8 ()1.4–1.8)	44% ()31–44%)
Influenza ( cepas estacionales)	Caídas respiratorias	1.3 ()1.2–1.4)	23% ()17–29%)
Yes hantavirus	gotitas respiratorias y fluidos corporales	1.2 ()0,8–1.6)	16% ()0–36%)
Virus de Nipah	Fluidos corporales	0.5	0%
MERS	Caídas respiratorias	0.5 ()0.3–0,8)	0%

Estimaciones para cepas de gripe.

Valores de R₀ y umbrales de inmunidad de rebaño (HITs) para cepas de gripe específicas
Enfermedad	Transmisión	R₀	HIT
Influenza (1918 cepa pandémica)	Caídas respiratorias	2	50%
Influenza (tasa pandemia de 2009)	Caídas respiratorias	1.6 ()1.3–2.0)	37% ()25–51%)
Influenza ( cepas estacionales)	Caídas respiratorias	1.3 ()1.2–1.4)	23% ()17–29%)

Estimaciones de variantes del SARS-CoV-2.

Valores de R₀ y umbrales de inmunidad de rebaño (HITs) para variantes de SARS-CoV-2
Enfermedad	Transmisión	R₀	HIT
COVID-19 (Variabilidad de Omicron)	Caídas respiratorias y aerosol	9.5	89%
COVID-19 (Vista de la delta)	Caídas respiratorias y aerosol	5.1	80%
COVID-19 (variante alfa)	Caídas respiratorias y aerosol	4 a 5	75-80%
COVID-19 (tracción solar)	Caídas respiratorias y aerosol	2.9 ()2.4–3.4)	65% ()58–71%)

En la cultura popular

En la película 2011 Contagion, un thriller de desastres médicos ficticios, cálculos de un blogger para ${displaystyle R_{0}}$ se presentan para reflejar la progresión de una infección viral fatal de casos aislados a una pandemia.

Contenido relacionado

Más resultados...